基于灰色層次分析法的察打型無人機作戰能力評估＊

楊 勇 吳 洋

（中國航天空氣動力技術研究院 北京 100074）

1 引言

察打一體化無人機系統較為復雜，其效能評估會牽涉到很多因素，其中部分評估參數可直接得到或精確計算后得到，但也有很多參數無法精確統計［1］。目前常用的評估方法都體現出對偵察型或攻擊型無人機作戰效能評估的概略性、相對性、局限性，但體系上無法實現有效的快速響應。另外，由于裝備數據保密等客觀條件的影響，具體到針對某型號的無人機效能評估方法很少具有可用性。

大量文獻表明評價無人偵察機系統作戰效能有多種方法［2］，如ADC法、指數分析法、概率法、計算機仿真法、群組層次分析法［3］等。本文針對無人機多數的參數指標只能通過模糊的、非定量的、難以精確定義的語言進行描述的情況，應用層次分析法和灰色綜合評判理論對某察打一體化無人機的作戰效能進行評估。首先運用層次分析法提出分析無人機作戰效能評價的指標體系，然后應用模糊理論的方法對不可量化和不精確的概念采用模糊隸屬函數進行處理［4］，從而對無人機作戰效能進行有效的綜合分析評估。

2 灰色層次分析法

2.1 層次分析法原理

層次分析法（Analytic Hierarchy Process，AHP）是一種計算作戰分系統各層次節點權重的方法，其基本原理［5］為：

1）針對特定功能的某類系統，分析其組成作戰任務的各個要素，并根據相互間的邏輯關系建立多層次結構分布表，假設存在被評判對象的指標集E，滿足E＝｛E1，E2，…，Ei｝［6］。

圖1 多層次結構分布邏輯關系圖

2）對同一層次的各要素按照其上一層次某一準則的重要性進行比較，并通過專家打分建立兩兩比較矩陣［7］。將其下層各個要素關于上層的重要性按照九等級分別打分，用aij來表示第i個要素相對于第j個要素的比較結果，可知aij＝1／aji。則比較矩陣A為

A實際上為一個正互反矩陣。

4）計算所有要素相對于系統的合成權重，整理后得到數學模型的系數［9］。

層次分析法作為一種針對多個層次下單準則評價的綜合評估方法，有著過分依賴專家系統、無法處理病態矩陣的缺陷［10］。

2.2 引入灰色理論后的改進

灰色系統理論著重研究概率統計，以及模糊數學難以解決的“小樣本，貧信息”不確定性問題。在層次分析法基礎上，將不同層次的決策權（數學表現為“權值”）使用灰色系統理論來重新計算，得到一種改進后的灰色層次分析法。

部分取代專家評估法的灰色統計要點為

1）確定評估灰類的等級數、灰類的灰數和灰類的白化權函數。根據具體層級的待評對象，通過定性分析確定。常用的灰數白化函數有：灰數為⊕∈（a1，∞），白化函數為f1（aji）；灰數為⊕∈（0，a12a1），白化函數為f2（aji）；灰數為⊕∈（0，a1，a1），白化函數為f3（aji）；

2）由和fk（aji）計算出被評估要素關于評估指標E屬于第k類的灰色評估系數，即h并寫出所有被評估要素對于評估指標的灰色評估權矩陣，即

由R（E）求得＝Maxk｛｝，得到指標評估權向量

進而得到不同被評估要素評為不同的灰類的總評估權。

3）綜合所有指標，對被評估要素進行效能評估，即Ei＝W×r，其中W為不同灰類的評估權系數。

3 察打一體化無人機作戰效能

3.1 作戰性能指標體系

層次分析法能夠確定察打一體化無人機的性能作戰指標，如圖2所示。根據層次分析法的基礎原理，分層越多，其最終評估結果就越精確［11］，此處分層到三級為止，未提及指標均為非重要指標，可暫時忽略。

圖2 某察打一體化無人機作戰效能體系

其中，三級指標“可靠性”又分為鏈路傳輸誤碼率E111、通常任務可靠度E112、平均無故障間隔時間E113；“機動性”又可分為定常轉彎角速率E121、最大允許過載E122、單位重量可用功率E123；“敏捷性”又可分為俯仰敏捷E131、滾轉敏捷E132、航向敏捷E133；“隱身性”又可分為機身輪廓大小E141、紅外輻射強度E142、最大雷達反射截面E143；“電子對抗性能”又可分為鏈路抗干擾性E151、全向自衛告警能力E152；“載荷探測能力”分為最遠探測距離E211、最大搜索方位角E212、目標跟蹤鎖定能力E213、目標定位能力E214；“載荷操縱能力”分為飛控操作手能力E221、操作手發現概率E222、臨場決斷能力E223。

3.2 層次分析求得特征向量

計算評估指標體系底層要素的組合權重，根據簡易表格打分法列出表格，其中以攻擊能力為例，打分表格如表3.1所示。

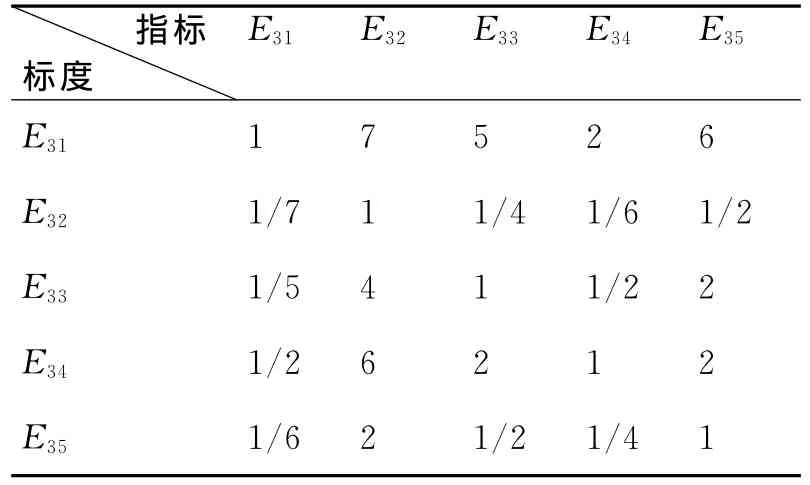
表1攻擊能力下層指標重要性打分表

將打分結果代入式（1）中，得到比較矩陣：

將A3的每一列向量歸一化處理，得到

計算得到特征權向量W3＝（0.4748，0.0459，0.1379，0.2658，0.0756）T，特征向量的分量可看作該相應因素對于目標的組合權重，應用同樣的原理，求得特征向量W1、W2。

得到的特征權向量需要經過一致性的驗證，定義一致性指標CI為

其中λmax表示最大特征值，n表示特征向量的分量個數。一般情況下，若CI≤0.1，就認為判斷矩陣具有一致性，據此而計算的值是可以接受的。然而，隨著n的增加判斷誤差就會增加，因此判斷一致性時應考慮到n的影響，可使用隨機一致性比值CR＝CI／RI，其中RI為平均隨機一致性指標。表2給出了判斷矩陣計算的平均隨機一致性指標檢驗值。

本實例中，n＝5，RI＝1.12，根據隨機性一致性比值公式可以計算得到CR＝0.0204，說明CR＜0.1，比較矩陣具有令人滿意的一致性。

表2 平均隨機一致性指標檢驗值對照表

3.3 待評估要素的評估矩陣和評估灰類

設專家組由五個評估者組成，分別為Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ。評估對象為攻擊能力E3的五個分要素性能指標。根據專家組評分，打分方式使用10分制，得到評估指標矩陣：

同理得DA1、DA2。

設有四個評估灰類“優”、“良”、“中”、“差”，其對應的灰數和白化權函數如圖3所示。

圖3 灰類的白化權函數

設第一類“優”k＝1，灰度系數⊕∈（9，∞）；第二類“良”k＝2，灰度系數⊕∈（0，8，16）；第三類“中”k＝3，灰度系數⊕∈（0，6，12）；第四類“優”k＝4，灰度系數⊕∈（0，1，5）。依次分別對應白化函數圖中的f1、f2、f3、f4。函數表示如下：

3.4 灰色評估系數、評估權向量與權矩陣

設有n名評估專家對m個指標進行評分，其中第j名專家對第i個指標的評估值為dij，則可得到目標的評估值矩陣：

則對于待評估指標E31屬于灰類k的評估權系數hik與總評估權系數hi為

根據評估系數hik和hi，計算得出評估指標i的灰色評估權向量ri

同理可得其他指標的灰色評估權向量，從而構成攻擊能力的評估權矩陣R

矩陣中的p表示指標的個數，通過式（13）、式（14）可得，本實例中的專家組評分結果DA3對應的評估權矩陣RA3為

3.5 灰色綜合評價

灰色綜合評價時，可以通過特征向量W3和評估權矩陣RA3計算得到無人機攻擊能力的灰度綜合評估值。根據之前得到的特征向量和評估權矩陣，得攻擊能力評估結果PA3＝W3RA3＝（0.3259，0.3620，0.3121，0）。同理可以得到生存能力和偵察能力的評估結果PA1、PA2。

根據灰類等級的劃分，可以將攻擊能力評估的結果對應到“優”，“良”，“中”，“差”四個等級，參照評估結果可以看到，本次評估中第2等級的權重最大，表明評估結果屬于等級“良”。在實際應用當中，可以將四個等級實體化，例如對于無人機作戰能力毀傷評估中，可表示為優（完全允許無人機再次出勤），良（基本允許無人機再次出勤），中（不建議無人機再次出勤）和差（無人機無法再次出勤）。根據仿真評估結果，相關作戰單位需要對攻擊能力中的相應技術環節進行修復和更替。

4 結語

隨著電子、控制等技術的突飛猛進，高技術戰爭武器越來越向無人控制方向發展，如何科學有效地對無人武器進行效能評估以達到快速響應重復出勤的目的是非常重要的。然而由于武器設備的高復雜性，使得在戰時環境下無法對各指標進行準確的定量測量，傳統的評估方法多為定性分析，無法真實地反應出實際情況。本文將層次分析法和灰色理論相結合，將灰色層次分析法應用于某察打型中空無人機作戰效能評估。文章以無人機攻擊能力為例，使用層次分析法對攻擊能力指標進行數學模型建立，并通過專家組評分和灰色理論對無人機攻擊能力進行了綜合的定量評價，計算結果能夠真實反映作戰能力，證明了此方法的有效。

文中在建立評估矩陣時使用了專家組評分，此方法仍然在較大程度上引入了人為的因素，使得評估結果存在主觀性判別誤差［12］，在下一步改進時，可用其他的評分算法代替專家打分的方法，以更為客觀地反映評估結果。另外，灰類等級劃分時選擇了傳統的“優良中差”四等級方式，雖然能夠在一定程度上真實反映出系統的情況，但是考慮到戰爭中的出勤效率，可以選擇更加細化的灰類等級劃分，建議選擇10等級、12等級或者更為科學的等級制，以提高評估的精度，達到更好的評估效果。

［1］汪民樂，高曉光，蔡付東.作戰飛機效能分析研究綜述［J］.飛行力學，2001，19（4）：1－2.

［2］俊紅.武器系統效能評估方法淺論［J］.火控雷達技術，2003，12（32）：47－50.

［3］林岳崢，祝利，程曉雷.基于群組層次分析法的情報保障系統效能評估［J］.兵工自動化，2012，31（8）：58－59.

［4］劉思峰，郭天榜，黨耀國.灰色系統理論及其應用［M］.北京：科學出版社，2000.

［5］郭齊勝，等.系統建模［M］.北京：國防工業出版社，2006，5：298－299.

［6］甄濤，等.地地導彈武器系統作戰效能評估方法［M］.北京：國防工業出版社，2005，1：249－259.

［7］Cheng C H.Evaluating naval tactical missile systems by fuzzy AHP based on the grade value of membership function［J］.European Journal of Operations Research，1996，96（2）：343－350.

［8］孫璐.層次分析法中用于確定權重的最?。畲髢灮椒ǎ跩］.東南大學學報，2012，8（2）：245－250.

［9］Chu A，Kalaba R，Springarn K.A comparison of two methods for determining the weights of belonging to fuzzy sets［J］.Journal of Optimization Theory and Applications，1979，27（4）：531－541.

［10］呂艷輝.基于AHP的灰色評估模型及其應用［J］.火力與指揮控制，2005（8）：80－82.

［11］吳輝，周洲，王蜀涵.偵察／打擊一體化無人機作戰效能分析方法研究［J］.飛行力學，2009，27（2）：31.

［12］謝季堅，劉承平.模糊數學方法及其應用［M］.武漢：華中理工大學出版社，2006.