基于Petri網的登陸作戰中協同通信的性能評價＊

于 夫

（92941部隊96分隊 葫蘆島 125000）

1 Petri網簡介

Petri網的概念最早在1962年Carl Adam Petri的博士論文中提出來。Petri的工作引起了歐美學術界與工業界的注意。1970年～1975年，MIT的計算結構研究小組積極參與Petri網相關的研究。到現在已出版了包括高級網在內的許多Petri網專著［1］。

這里首先引出Petri網的一般概念：

定義1 當一個三元組N＝（S，T；F）是一個Petri網if（當且僅當）：

1）S∪T≠φ（網非空）；

2）S∩T≠φ（二元性）；

3）F?（S×T）∪（T×S）（流關系僅在S與T的元素之間）；

4）dom（F）∪cod（F）＝S∪T（沒有孤立元素）。

在網中，F的元素叫弧，dom（F）＝｛x｜?y：（x，y）∈F｝，cod（F）＝｛x｜?y：（y，x）∈F｝。

在圖形上，S元素用一個圓圈表示，代表位置；T元素用一個四方形或者長方形表示，但常常為了節省空間，僅用一段黑線表示。在X元素之間的流關系由帶箭頭的弧表示，其方法如下：

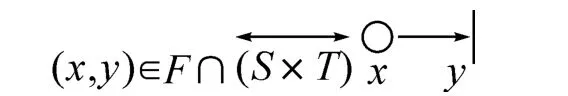
定義2 隨機Petri網SPN（stochastic Petri net）

近年來，人們以各種方式把時間引入Petri網，其中常見的有兩種引入方式：一是每個位置相關聯一個時間參數；二是每個變遷相關聯一個時間參數。另外一種在Petri網中引入時間參數的方法是：在每個變遷的可實施與實施之間聯系一個隨機的延遲時間，這種類型的Petri網叫做隨機Petri網。

給Petri網的每個變遷相關聯一個實施速率（firing rate），得到的模型就是SPN［2］。

在連續時間隨機Petri網中，一個變遷從可實施到實施需要延時，即從一個變遷t變成可實施的時刻到它實施時刻之間被看成是一個連續隨機變量xi（取正實數值），且服從于一個分布函數：

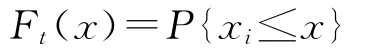
在不同類型的連續時間隨機網中，這個分布函數的定義是不一樣的。當相關于每個變遷的分布函數定義成一個指數分布函數：

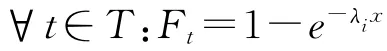
其中實參數λt＞0是變遷t的平均實施速率，變量x≥0。可證明：

1）兩個變遷在同一時刻實施的概率為零；

2）SPN的可達圖同構于一個齊次 MC，因而可用馬爾可夫隨過程求解。

指數分布是滿足馬爾可夫特性的連續隨機變量的惟一分布函數。因此，要想把馬爾可夫隨機過程應用于SPN的可達圖，每個變遷的延時服從于指數分布是充要條件。

2 運用SPN分析登陸作戰中協同通信系統性能的可能性

對于登陸作戰而言，參加作戰的陸、海、空三軍及二炮部隊均需得到各方的協同；又因登陸作戰中敵防御前沿支撐點多，高技術兵器多，可以認為：在登陸作戰中，各軍兵種必然和多個方向建立協同通信，并且協同通信呼叫率是相當大的［3］。而對有大量用戶所形成的呼叫流來說，它們所形成的呼叫流可以看成是一個無后效流，一般大數量的獨立信源的來話呼叫可認為是一種泊松呼叫流，即在時間長度t內，恰好發生k次呼叫的概率服從泊松分布：

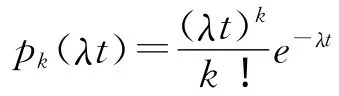
式中λ為平均到達率，即隨機變量的數學期望。

由上式不難求出在t秒內k次或大于k次呼叫的概率：

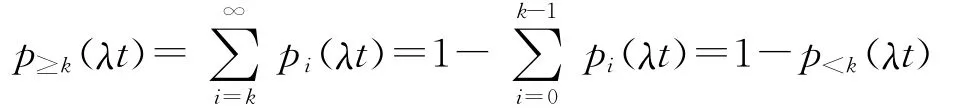
因此，在t時間內沒有發生呼叫（k＝0）的概率為p0（λt）＝e－λt。因此，不難求出呼叫之間的時間間隔的概率分布F（t）。按照隨機變量分布函數的定義，F（t）等于呼叫間隔η小于給定值t的概率，即在時間長度t內發生一個或一個以上呼叫的概率，所以有：

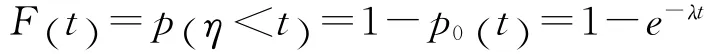
可見，在泊松流情況下，呼叫時間間隔的分布為指數分布。因此，協同通信系統的呼叫流服從指數分布，可以用馬爾可夫鏈等效SPN可達圖來分析系統性能［4］。

3 SPN建模分析

SPN應用在系統模型的性能分析中分為三步：

1）給出系統的一個SPN模型；

2）構造出該SPN所同構的MC；

3）基于MC的穩定狀態概率進行所要求的系統性能分析。

下面用SPN理論來分析登陸作戰中集團軍利用協同通信分隊組成此網的時延情況。

集團軍內各作戰群在作戰過程中的協同通信決策過程如圖1所示。

根據以上分析，建立如圖2所示的Petri網：

圖中○表示位置，用P表示，｜代表事件發生的條件，→表示變遷，用t表示，代表事件的發生。

圖2 基于Petri網的協同通信決策流程圖

圖中共有11個位置和14個變遷，為了表示協同通信動作的重復性，在變遷t13和位置P1，變遷t14和位置P1之間通過有向弧進行連接，分別表示各兵種間協同和軍種間協同。變遷的實施速率λ表示在可實施的情況下單位時間內平均實施次數，在各次變遷中是不同的，根據作戰實際情況，其平均實施速率集為λ＝（11111111212111）在初始位置P1有標識，如圖示（即有敵情需協同作戰），初始狀態M1＝（10000000000），由M1出發經不同的變遷可得如下Petri網狀態：

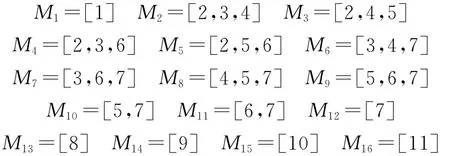
等效于如圖3所示馬爾可夫鏈。

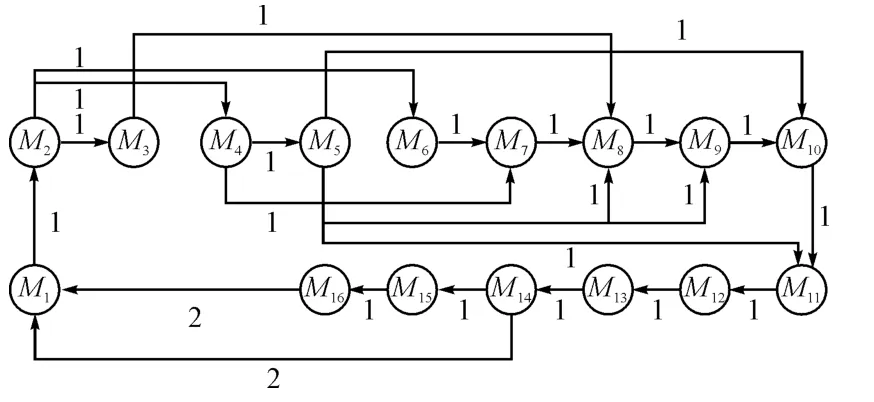
圖3 馬爾可夫鏈

根據以上所得，可以列n＋1個齊次方程，含有n（n＝16）個未知變量，加上∑ixi＝1，即可求出每個可達標識的穩定概率：

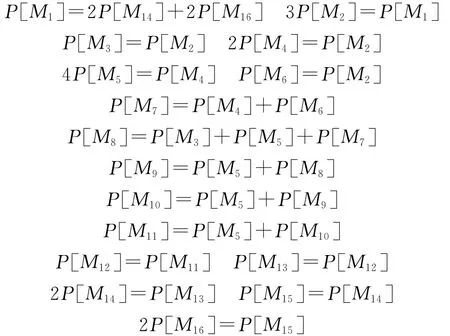
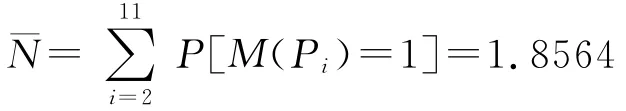
由穩定狀態下流量關系的Little公式ˉN＝ˉλˉT，ˉT為t1的平均發射時間，它是平均發射率的倒數，即ˉT＝1／λ＝1，ˉλ表示通過t1的平均流量，于是ˉλ＝0.1076。我們可以利用Little規則和平衡原理，計算非零回歸的MC，子系統的流入流出速率應該平衡（相等）。根據Petri網性質，t1一旦發射，它將向P2、P3、P4各輸出一個標識，故t1－t14之間的總流量是＝3＝0.3228。

子系統的平均延時時間為

在作戰忙時（搶灘上陸和建立登陸場），由于各種障礙物及火力點眾多，加之敵強調先制與反制作戰，敵必然將各類兵力、兵器靠前配置并大量集中使用于此階段，戰役任務將極為艱巨，作戰協同任務繁重，一梯隊集團軍內各單位呼叫協同及集團軍向各軍種呼叫協同率合計約為200次／小時，即λ＝3.33（次／分鐘），平均每次呼叫間隔18s，各協同通信分隊發出協同通信信息需要的時間為2個單位時間，整個協同通信系統的期望時延為18×2×5.75＝207s＝3.45min。

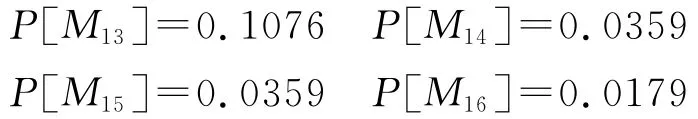
在穩定狀態下，每個位置中所包含的標記數量的概率，對?s∈S，?i∈N，令P［M（s）＝i］表示位置s中包含i個標記的概率，即可從標識的穩定概率求得位置s的標記概率密度函數如下

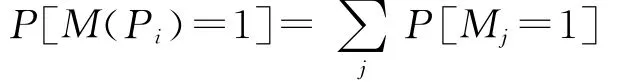
其中Mj∈［M0］，且Mj（s）＝i。

由此可求出子系統位置集所含的平均標記數：

4 結語

由上文SPN分析可知，登陸作戰中集團軍內部組織協同通信網，協同動作的延時時間約為3.45min，比傳統的作戰協同通信具有更高的效率，能夠更有效地保證大型島嶼聯合進攻作戰的協同。本文對登陸作戰中協同通信研究有一定借鑒意義。

［1］林闖.隨機Petri網和系統性能評價［M］.北京：清華大學出版社，2000：302－311.

［2］高東華.登陸作戰中電子對抗戰術運用［C］／／趙利德主編.98煙臺學術研討會論文集.北京：中國人民解放軍射擊學會，1998：96－99.

［3］魏碧海.海南島戰役渡海登陸作戰的歷史經驗與思考［J］.軍事歷史，2001：33－35.

［4］王作超.集團軍登島作戰通信需求分析系統研究報告［J］.重慶：通信指揮學院，2000：100－105.

［5］唐春生.現代登陸戰役電子戰法研究［J］.海軍學術研究，1995，1：82－83.

［6］王新建.信息化條件下登陸作戰探析［J］.國防大學學報，2007，1：30－32.

［7］高東華.艦艇電子對抗作戰指揮［M］.北京：海潮出版社，2002，4：100－102.

［8］齊德學.中外登陸作戰經驗教訓［M］.北京：軍事科學出版社，2006：24－26.