一種利用修正牛頓迭代的時差定位算法

朱國輝,馮大政,李 進,周 延

(西安電子科技大學雷達信號處理國家重點實驗室,陜西西安 710071)

一種利用修正牛頓迭代的時差定位算法

朱國輝,馮大政,李 進,周 延

(西安電子科技大學雷達信號處理國家重點實驗室,陜西西安 710071)

針對傳統基于迭代求解的時差定位算法中容易出現的發散問題,提出了一種新的基于修正牛頓迭代的時差定位算法.該算法首先利用輔助變量將非線性時差定位方程組轉化為一組關于輻射源位置的偽線性方程,在此基礎上把時差定位問題轉化為約束加權最小二乘優化問題;然后,利用基于特征值修正的牛頓法進行定位解算,同時為了減少迭代次數,通過二次插值法對一維優化問題進行尋優求解,給出了迭代步長因子的求取過程;最后,通過仿真分析驗證了所提算法的有效性.

無源定位;到達時間差;加權最小二乘估計;修正牛頓法;二次插值法

與傳統的有源定位系統相比,無源定位技術具有隱蔽性強的優點,在雷達[1]、聲納[2]、無線通信和傳感器網絡[3]等領域有著廣泛的應用.常用的無源定位技術包括基于到達時間、基于到達時間差和基于到達角的定位算法[4-7].基于多站時差的定位技術對接收系統的要求較低,具有定位成本低、精度較高等優點,因而受到越來越多的關注.

時差定位問題本質上是一個高度非線性估計問題,可用最大似然估計方法處理.在測量噪聲服從高斯分布的前提下,最大似然估計將時差定位問題轉化為非線性最小二乘求解問題,通常是利用迭代方法進行求解,且需要一個迭代初始值.目前常見的基于迭代求解的時差定位算法有泰勒級數法[8]、牛頓法[9]等,它們是一類需要初始估計位置的迭代算法,主要缺點是其收斂性非常依賴于目標函數的非線性程度和迭代初始值的精度.當用一組接近真實值的初始值進行迭代求解時,能夠獲得超線性乃至二次收斂速度[10],定位精度高.但是在初始值選擇不好的情況下,迭代過程中容易落入到局部極小點,而且不能保證其收斂性.為此,筆者提出了一種新的基于迭代求解的時差定位算法.該算法首先通過對非線性時差定位方程進行轉換,得到較規則的目標函數;然后在迭代過程中對海森矩陣進行特征值修正,在一定程度上避免了傳統基于迭代求解的定位算法因矩陣奇異引起的發散現象,同時通過二次插值法求解迭代步長因子,有效減少了迭代次數.仿真結果驗證了所提算法的有效性.

1 時差定位模型

輻射源u到接收站si的距離為

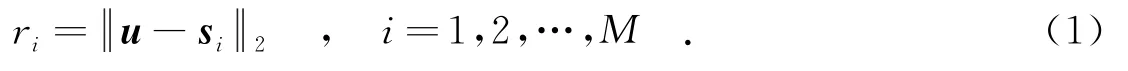
不失一般性,選取s1作為參考接收站,不考慮非視距傳播的影響,可以得到時差定位方程為

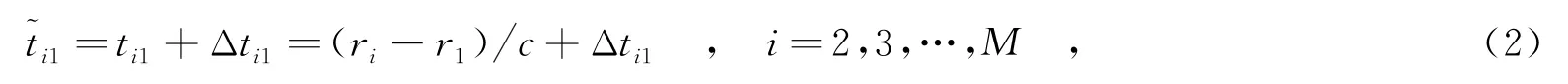
其中,ni1=cΔti1,表示相應的距離差測量誤差.令fi1(u)=ri-r1,將式(3)寫成矢量形式為

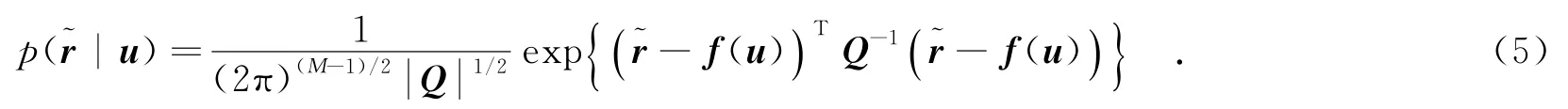
最大化式(5),似然函數可以轉換為極小化二次型目標函數[11],即

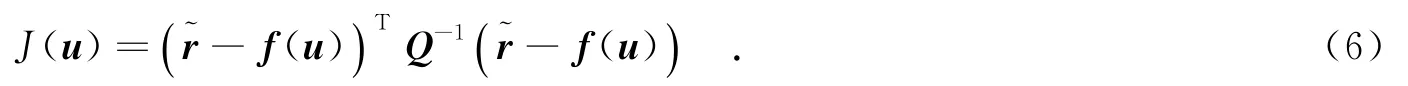
式(6)為關于輻射源位置的非線性目標函數,沒有封閉解.

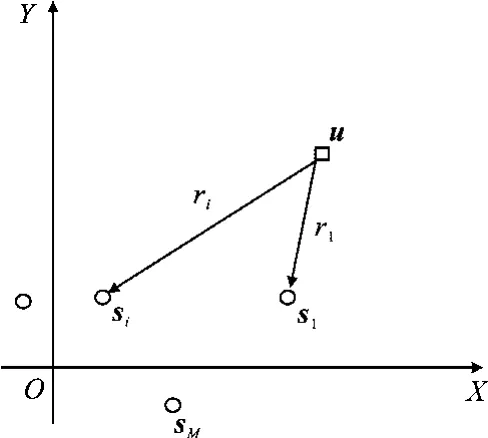
圖1 無源時差定位示意圖

2 基于修正牛頓迭代的時差定位算法

2.1 加權最小二乘估計

由式(1)可知,時差定位模型式(3)是關于目標位置的高度非線性函數,由此得到的目標函數式(6)的幾何結構很不規則,并且存在局部極小點[12].為此,首先將時差定位問題轉化為約束加權最小二乘問題,將式(3)右端的r1移至左端,兩邊同時平方,得

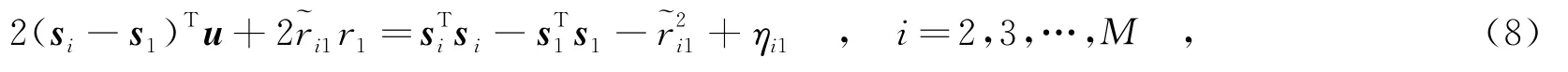
其中,η=2Bn,B=diag{r2,…,rM}.對近似方程Aθ≈b,進行加權最小二乘估計求解,可得

其中,g=[g2,…,gM]T.可在式(11)的基礎上進行迭代求解.

2.2 基于修正牛頓迭代的時差定位算法

其中,Gu0和Hu0分別為目標函數在給定初始值u0下的梯度矢量和海森矩陣.將式(10)得到的結果作為初始值進行迭代,直到收斂.當初始值u0距極小點較遠時,可能出現海森矩陣奇異的情形,此時不能確定下一步的迭代值;即使海森矩陣可逆,也可能是非正定矩陣,由此得到的搜索方向不一定是下降方向,如按式(12)進行迭代,目標函數值可能上升,這就導致算法失效.針對這些問題,提出一種基于特征值修正的牛頓法.

2.2.1 特征值修正

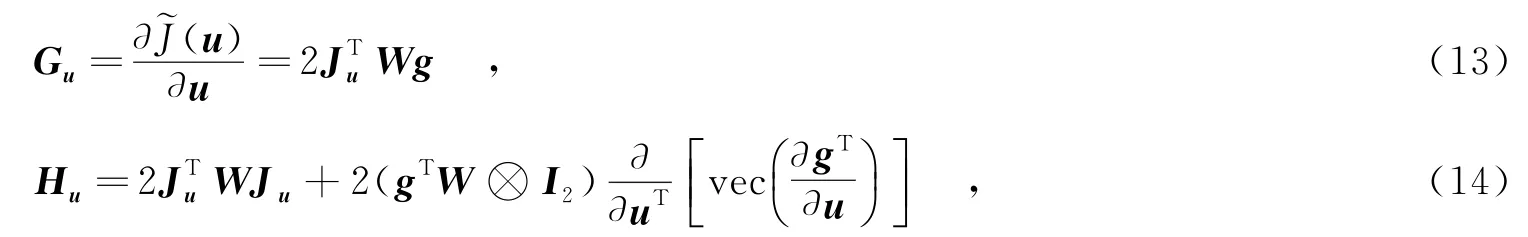
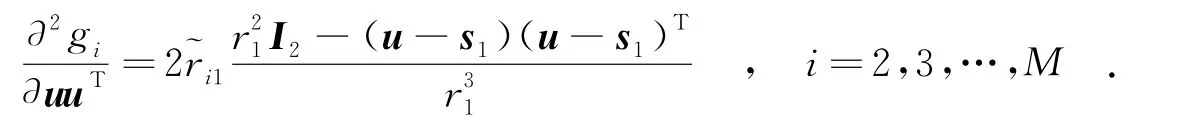
將矩陣Hu進行特征值分解得:Hu=UΛUT,其中,Λ=diag{ρ1,ρ2},U為相應的特征向量組成的矩陣.設ρ1和 ρ2已按從大到小的順序排列,若ρ1和ρ2均為正數,則Hu為正定矩陣,取搜索方向若ρ1和ρ2均為負,取?Λ=-Λ;若ρ2＜0,取?Λ=diag{ρ1,ρ1},則修正后的海森矩陣為修正后的海森矩陣的特征值均大于零,取搜索方向即為下降方向.給定任意迭代初始值,修正后的海森矩陣滿足對稱正定性.

2.2.2 步長因子λ的選取

引入迭代步長因子λ,使得每次迭代過程中,目標函數在下降方向上更接近極小值.一般來說,將代入目標函數使目標函數最小的λ即為所求.這種精確搜索往往需要進行迭代求解,計算量大,特別是當初始值遠離最優解時,效率很低;而且很多優化算法的收斂速度并不依賴于精確的搜索過程.因此,提出了一種基于二次插值法的步長因子選取方法,令構造二次多項式p(λ)=a+bλ+cλ2,將其極小點作為φ(λ)真實極小點的近似.當λ=0時,令

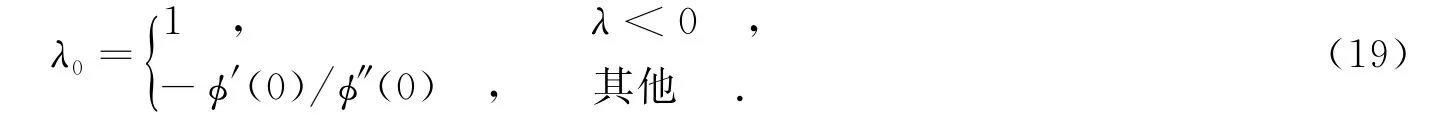
修正牛頓法的步驟如下:

(1)根據式(10)求取初始值u0,允許誤差ε＞0[12],令k∶=0.

(4)根據式(19)求取迭代步長因子λk.

3 性能分析

由于泰勒級數法和高斯牛頓法在實質上等價[12],為方便討論,稱基于目標函數的泰勒級數法為高斯牛頓法.為了檢驗文中算法對輻射源位置估計的性能,進行了下述的仿真實驗,并將該算法與基于J(u)的泰勒級數法、基于的高斯牛頓法、牛頓法及克拉美羅界的仿真結果進行比較,各算法的迭代停止條件均為.假設有4個接收站參與定位,坐標分別為[20,1]T,這里及下面仿真實驗中的輻射源坐標單位均為米.噪聲協方差矩陣Q是對角線元素為非對角線元素[13]為的對稱矩陣.采用位置估計的均方根誤差對各算法的定位性能進行衡量,其定義式為

仿真1輻射源位置坐標為[10,30]T,x∈[-100,100],y∈[-100,100].取(4BQBT)-1.圖2(a)～(c)分別給出了目標函數J(u)在權W0及目標函數在權W0和最優權W1下隨x和y變化的函數取值示意圖.從圖2(a)可以看出,目標函數J(u)的幾何結構很不規則,這就對迭代初始值的選取要求很高,用傳統優化算法進行迭代求解時較難得到正確結果.從圖2(b)和圖2(c)可以看出,目標函數)在權W0和最優權W1下的幾何結構相似,在y軸方向上較為平坦,但避免了局部極小點,與圖2(a)相比有很大改善,幾何結構較為規則,能較易收斂到正確的結果,這也在下面的仿真中得到驗證.

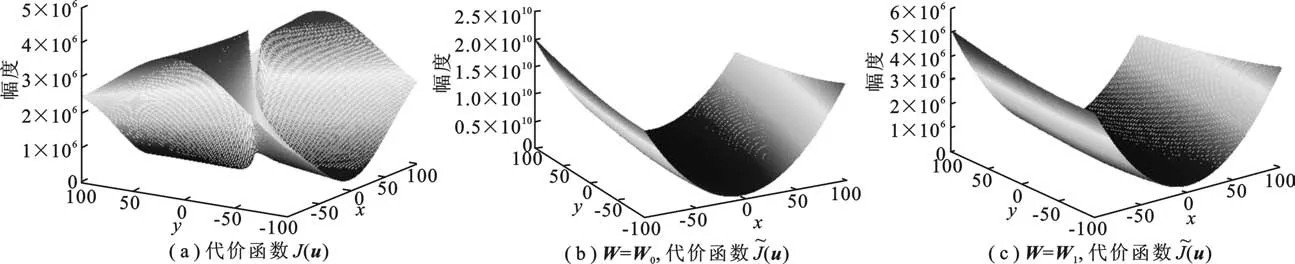
圖2 目標函數J(u)及隨x和y變化的函數取值示意圖

仿真2近場輻射源位置坐標為[20,12]T,噪聲功率從10-3.5變化到101.2,將式(10)所得結果作為各算法的迭代初始值.圖3(a)和圖3(b)分別為各算法隨噪聲功率變化的平均迭代次數和均方根誤差的統計結果,式(11)中W=W0.從圖3(a)和圖3(b)可以看出,在噪聲功率較小時,各算法對輻射源位置估計的均方根誤差均接近克拉美羅界,所需平均迭代次數也相當.隨著噪聲功率的增加,泰勒級數法的平均迭代次數保持最小,但其估計均方根誤差迅速增加,而文中算法并沒有出現性能急劇下降的現象,定位精度與高斯牛頓法、牛頓法相當,說明了目標函數具有較好的幾何結構.但高斯牛頓法和牛頓法理論上仍然存在發散的可能性.文中算法的單步迭代計算量要小于高斯牛頓法和牛頓法的計算量,但從圖3可以看出,當噪聲功率較大時,迭代次數要明顯小于它們.最后,文中算法、高斯牛頓法和牛頓法的均方根誤差會出現低于克拉美羅界的現象,這是因為在測量誤差較大時,式(7)中的高階誤差項不能忽略不計,這時各算法是有偏估計的,而克拉美羅界是所有無偏估計所能達到的下界.

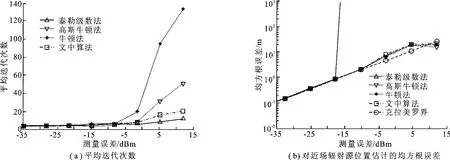
圖3 各算法對近場輻射源位置的定位性能示意圖

仿真3遠場輻射源位置坐標為[300,220]T,噪聲功率從10-6變化到10-2,各算法迭代初始值的選取同仿真2.圖4(a)和圖4(b)分別給出了各算法對遠場輻射源位置估計隨噪聲功率變化的平均迭代次數和均方根誤差的統計結果.從圖4(a)和圖4(b)可以得出與仿真2類似的結論,在噪聲功率較小時,各算法對輻射源位置估計的均方根誤差均接近克拉美羅界.基于目標函數J(u)的泰勒級數法平均迭代次數較少,但是隨著測量誤差的增加,其均方根誤差迅速增加.而基于目標函數的文中算法并沒有出現性能急劇下降的現象,迭代次數要明顯小于高斯牛頓法和牛頓法的迭代次數,定位精度稍優于高斯牛頓法的定位精度,這是因為高斯牛頓法等價于目標函數的一階近似.最后,文中算法、高斯牛頓法和牛頓法的均方根誤差會出現類似于仿真2中低于克拉美羅界的現象,原因同仿真2中的說明.

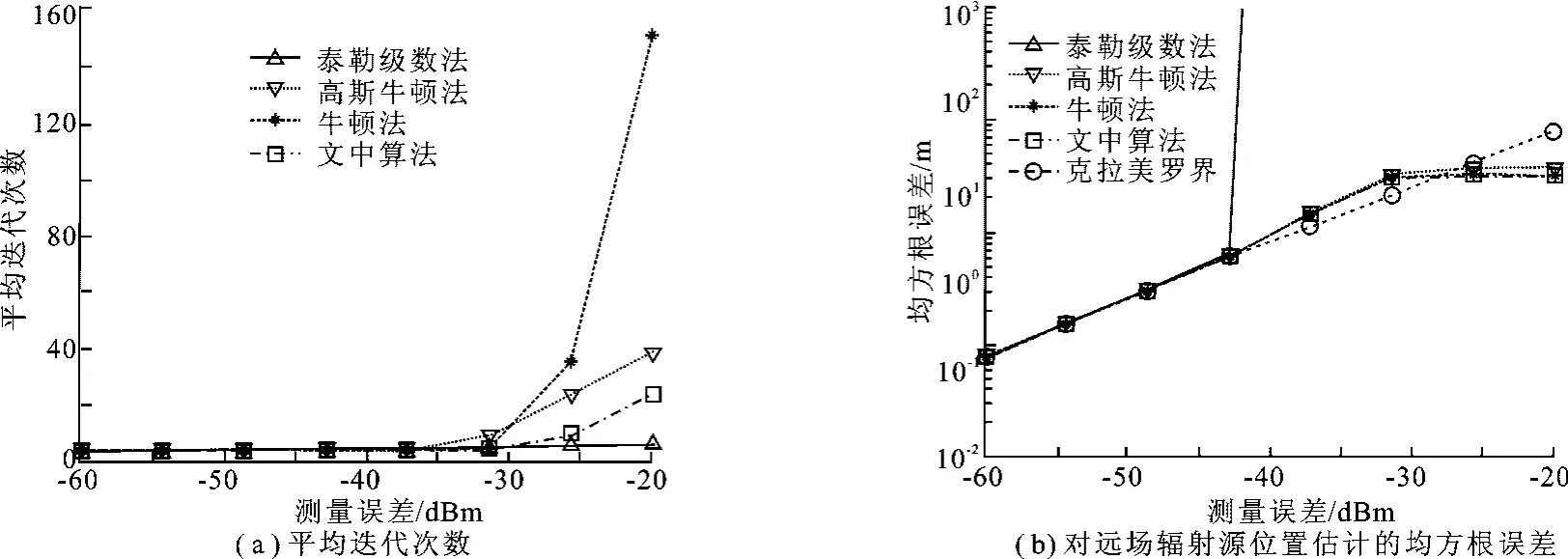
圖4 各算法對遠場輻射源位置的定位性能示意圖

4 結束語

針對傳統基于迭代求解的時差定位算法中出現的發散問題,提出了一種基于修正牛頓迭代的時差定位算法.通過引入輔助變量將高度非線性定位問題轉化為約束加權最小二乘問題,求取較規則的目標函數,并在此基礎上利用修正牛頓法進行迭代求解.所提算法一方面采取特征值修正避免了傳統迭代算法因矩陣奇異出現的發散問題,另一方面采用二次插值法求取迭代步長因子減少了迭代次數,具有較好的定位性能.當測量誤差較大時,文中算法忽略了高階誤差項對均值和其他統計特性帶來的影響.如何根據高階誤差項的統計特性進行更好的定位,是今后研究的方向.

參考文獻:

[1]Min Jiang,Niu Ruixin,Blum R S.Bayesian Target Location and Velocity Estimation for Multiple-input Multiple-output Radar[J].IET Radar,Sonar and Navigation,2011,5(6):666-670.

[2]Fluckiger M,Neild A,Nelson B J.Optimization of Receiver Arrangements for Passive Emitter Localization Methods [J].Ultrasonics,2012,52(3):447-455.

[3]Gholami M,Cai Ningxu,Brennan R W.Evaluating Alternative Approaches to Mobile Object Localization in Wireless Sensor Networks with Passive Architecture[J].Computers in Industry,2012,63(9):941-947.

[4]牛新亮,趙國慶,劉原華,等.低空目標高精度無源時差定位方法[J].西安電子科技大學學報,2009,36(5):862-866.

Niu Xinliang,Zhao Guoqing,Liu Yuanhua,et al.High Precision Passive TDOA Location Method for Low-altitude Targets[J].Journal of Xidian University,2009,36(5):862-866.

[5]Annibale P,Filos J,Nyalor P,et al.TDOA Based Speed of Sound Estimation for a Temperature and Room Geometry Inference[J].IEEE Transactions on Audio,Speech,Language and Signal Processing,2013,21(2):234-246.

[6]Cheung K W,So H C.A Multidimensional Scaling Framework for Mobile Location Using Time-of-arrival Measurements [J].IEEE Transactions on Signal Processing,2005,53(2):460-470.

[7]同非,王俊,李紅偉.Memetic優化的外輻射源雷達方位-多普勒定位方法[J].西安電子科技大學學報,2012,39(4): 46-51.

Tong Fei,Wang Jun,Li Hongwei.Novel Passive Radar Location Algorithm Based on Memetic Optimization by Using the Bearing-and-Doppler Frequency[J].Journal of Xidian University,2012,39(4):46-51.

[8]Foy W H.Position-location Solution by Taylor-series Estimation[J].IEEE Transactions on Aerospace and Electronic Systems,1976,12(2):187-194.

[9]Liu Ying,Zhang Xu,Liu Dan,et al.Study of Location Algorithm for Wireless Sensor Networks Based on Newton Iteration[J].Advanced Materials Research,2013,645:285-289.

[10]袁亞湘,孫文瑜.最優化理論與方法[M].北京:科學出版社,1997.

[11]Torrieri D J.Statistical Theory of Passive Location Systems[J].IEEE Transactions on Aerospace and Electronic Systems,1984,20(2):183-198.

[12]Dogancay K,Sakhtsari A H.Target Tracking by Time of Difference of Arrival Using Recursive Smoothing[J].Signal Processing,2005,85(4):667-679.

[13]Chan Y T,Ho K C.A Simple and Efficient Estimator for Hyperbolic Location[J].IEEE Transactions on Signal Processing,1994,42(8):1905-1915.

(編輯:齊淑娟)

簡 訊

近日,在“2014年英特爾杯嵌入式系統專題邀請賽”中,西安電子科技大學應邀參賽的4支代表隊全部獲獎.其中,“基于視覺體感雙平衡的防暈動系統”奪得本次大賽的最高獎項“Intel杯”.嵌入式系統專題邀請賽自2002年舉辦首屆競賽以來,到2014年已成功舉辦了七屆.今年共有來自15個國家和地區的83所高校,170支隊伍參加.我校另三支參賽隊分獲二、三等獎.

(摘自《西電科大報》2014.8.14)

TDOA location algorithm based on modified Newton iterations

ZHU Guohui,FENG Dazheng,LI Jin,ZHOU Yan
(National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China)

For the divergence problem of traditional iterative process based location algorithms,a new modified Newton algorithm for the passive location from time differences of arrival(TDOA)is proposed. The proposed algorithm firstly reorganizes the nonlinear TDOA equations into pseudo-linear ones by using an auxiliary parameter,and a constrained weighted least-squares minimization is developed for the positioning problem instead of the Maximum Likelihood estimator.A modified Newton method based on eigenvalue modification is then applied to obtain the emitter position.In order to reduce the number of iterations,an appropriate iteration step size is computed via one-dimensional optimization by the quadratic interpolation method.Simulation results demonstrate the effectiveness of the proposed algorithm.

passive location;time difference of arrival;weighted least squares estimates;modified Newton algorithm;quadratic interpolation method

TN97

A

1001-2400(2014)05-0036-06

2013-06-24< class="emphasis_bold">網絡出版時間:

時間:2014-01-12

國家自然科學基金資助項目(61271293)

朱國輝(1987-),男,西安電子科技大學博士研究生,E-mail:zhugh@stu.xidian.edu.cn.

http://www.cnki.net/kcms/doi/10.3969/j.issn.1001-2400.2014.05.007.html

10.3969/j.issn.1001-2400.2014.05.007