基于經驗模態分解的橋式起重機振動模態分析
施科益 寧波市特種設備檢驗研究院
大噸位橋式起重機運行環境復雜,起重載荷、外部激勵等因素所產生的振動對起重機結構、承軌梁及廠房造成了破壞。采用有限元分析方法可以有效分析橋式起重機的固有頻率,使起重機避開其在使用過程中的外部激振頻率[1-2]。該方法在起重機設計時具有較強的指導意義,但由于其計算精度不足和起重機實際制造水平的影響,有限元分析對于在用、維修和改造的起重機的模態分析結果并不理想。
對于復雜的起重機械,其振動信號往往存在非平穩特性。一般的平穩信號處理方法就不能勝任了。利用經驗模態分解(Empirical Mode Decomposition,EMD)方法進行橋式起重機的模態分析具有較好的效果。EMD是一種自適應的時頻處理方法,特別適用于非線性、非平穩信號的分析處理[3]。以模態分析理論為基礎,通過對橋式起重機振動特性研究及其振動響應EMD分析,提出基于EMD的橋式起重機振動模態分析方法,并進行了仿真與實驗研究,驗證其在橋式起重機模態分析中的有效性。
1 機械系統模態分析理論
對于機械系統的振動問題,需要采用多自由度系統的振動理論分析。一個具有n個自由度的機械系統,在任一瞬時的運動形態要用n個獨立的廣義坐標描述,系統的運動微分方程一般是n個相互耦合的二階常微分方程組成的方程組。對n自由度的無阻尼系統而言,具有n個固有頻率,當系統按其中任意一個固有頻率作自由振動時,系統的運動是一種同步運動,稱為主振動。系統作主振動時所具有的振動形態稱為主振型,或稱為主模態[4]。對于多自由度的振動分析,通常采取振型疊加法,即選取主坐標,將n自由度系統的振動視為n個單自由度系統振動的疊加。
根據牛頓第二定律,建立n自由度機械系統的固有振動方程:

式中:M——n階質量矩陣;
K——n階剛度矩陣。
根據振型疊加法,主振動可設為
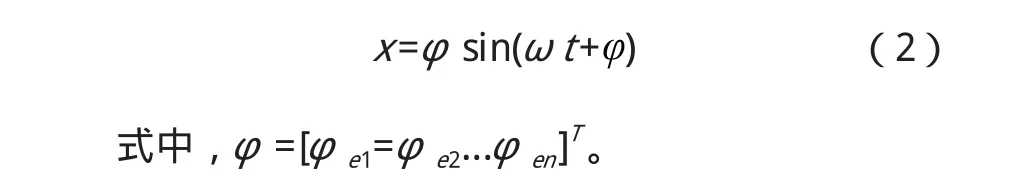
將式(2)代入式(1),根據正定系統的振動特點,可解得
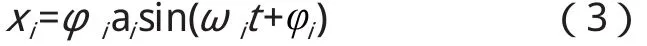
式中:φi稱為第i階主振型,也稱作主模態;ai為常數;ωi為第i階固有頻率。
式(3)稱為第i階主振動模式。與固有頻率一樣,系統的主振型僅取決于系統的質量矩陣M、剛度矩陣K等物理參數。
當式(3)中i由1取到n時,就得到了系統的n個主振動模式,因此,n自由度系統的固有振動即為n個主振動模式的疊加,即
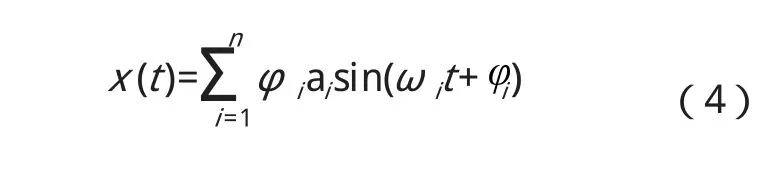
式(4)中,ai、為待定常數,由初始條件確定。
2 經驗模態分解法
EMD方法的基本思想是將原始信號分解成一系列固有模式函數(Intrinsic Mode Function,IMF)的組合,然后根據實際需要,對各個IMF利用進行后續的處理分析。
EMD方法建立在以下的假設基礎之上[3,5]:(1)信號至少有兩個極值點,一個極大值和一個極小值;(2)特征時間尺度通過兩個極值點之間的時間長度定義;(3)若信號數據缺乏極值點,但存在變形點,則可通過數據微分獲得極值點,然后再通過積分來獲得分解結果。一個IMF必須滿足兩個條件:(1)整個數據長度中極值點和過零點的數目必須相等或至多相差一個;(2)在任意數據點,局部極大值的包絡和局部極小值的包絡的均值須為零,即信號關于時間軸局部對稱。
EMD的分解過程,可以描述如下[6]:
(1)確定信號x(t)的局部極大值和極小值,將所有極大值和極小值用三次樣條插值函數插值形成數據的上下包絡線,上下包絡線的平均值記為m1(t),求得:
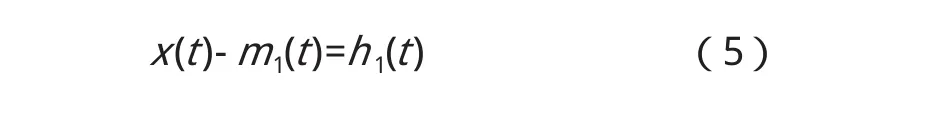
如果h1(t)是一個IMF,那么h1(t)就是x(t)的第一個分量;
(2)一般h1(t)不滿足IMF條件,此時把h1(t)作為原始數據,重復步驟(1),反復篩選k次,得到h1k(t)=h1k-1(t)-m1k(t),使得h1k(t)滿足IMF條件,記c1(t)=h1k(t),稱c1(t)為信號x(t)的第一階IMF;
(3) 將c1(t)從x(t)分離出來,得到殘余量r1(t)=x(t)-c1(t),把r1(t)作為原始數據重復步驟(1)、(2),從高頻至低頻可依次得到多階固有模態分量ci(t)和殘余量rn(t)。
整個過程遇到如下一個準則即終止:(1)分量cn(t)或殘余量rn(t)足夠小;(2)當殘余量rn(t)作為一個單調函數不能再提取滿足IMF時。最終原始信號x(t)可表示如下式:
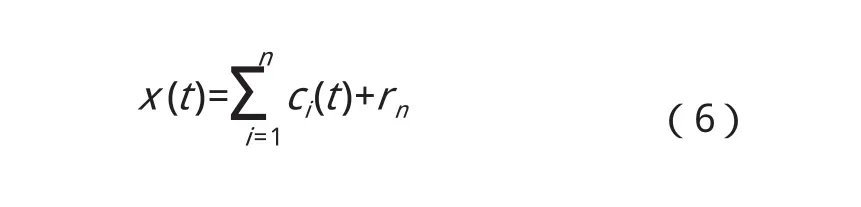
因此可以把任何一個信號x(t)分解成為n個IMF和一個殘余量之和,固有模態分量分別包含了信號從高到低不同頻率段的成分,且具有自適應性。
3 橋式起重機的EMD分析
以橋式起重機為對象,采用EMD方法進行振動模態分析。將橋式起重機簡化為一勻質等截面的簡支梁模型[7],兩端支撐限制垂直位移,一端同時限制水平位移,如圖1所示。

圖1 橋式起重機簡化模型
以y=y(x,t)表示梁的振動位移,以ρ A表示梁單元長度的質量,EI為截面抗彎剛度,設梁上作用有單位長度的分布力F(x,t),如圖2所示。
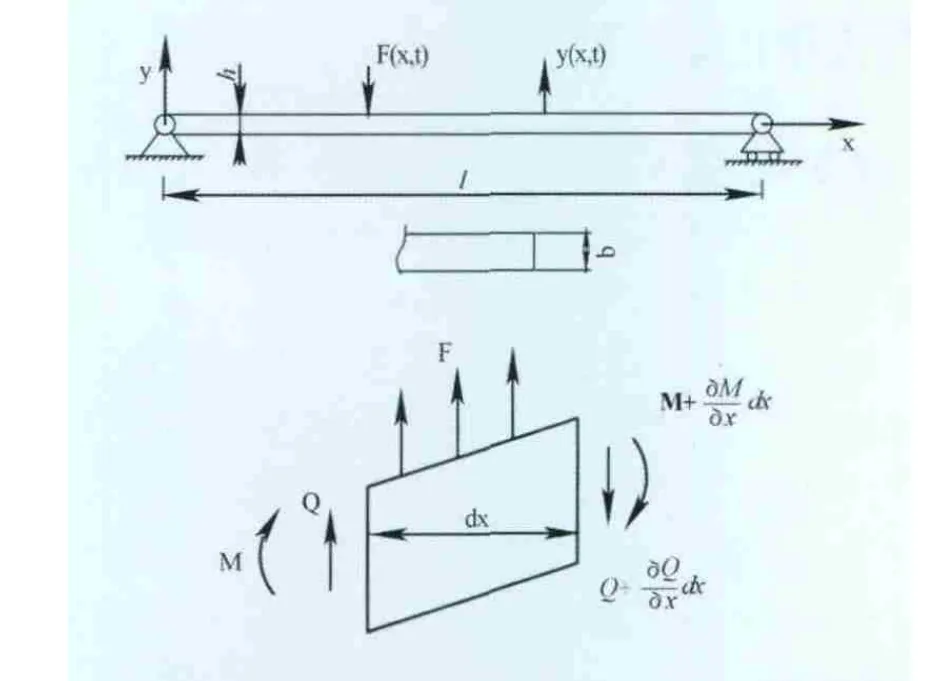
圖2 簡支梁振動模型
在梁的任意截面x處取一微段dx,其質量為ρAdx。受剪力Q(x,t)、彎矩M(x,t)和分布激擾力F(x,t)dx的作用。根據牛頓第二定律,在y方向的運動方程為:
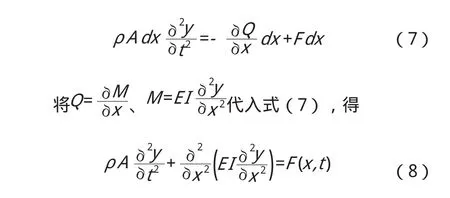
對于自由振動,設F(x,t)=0,求解系統各階主振動為:
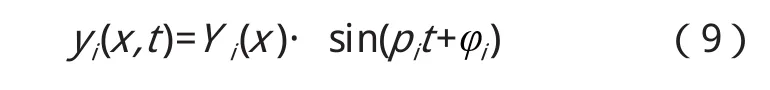
式中,Yi(x)為各階振型函數。固有頻率為:
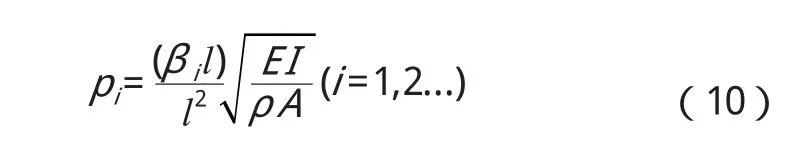
根據邊界條件Y(0)=Y(l)=0,Y(0)=Y(l)=0,可求得 Yi(x)=Ci·sinβix,其中Ci為常數,βil=iπ(i=1,2...)。對于任意位置x0,其自由振動響應。
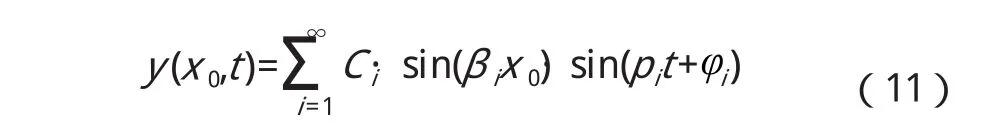
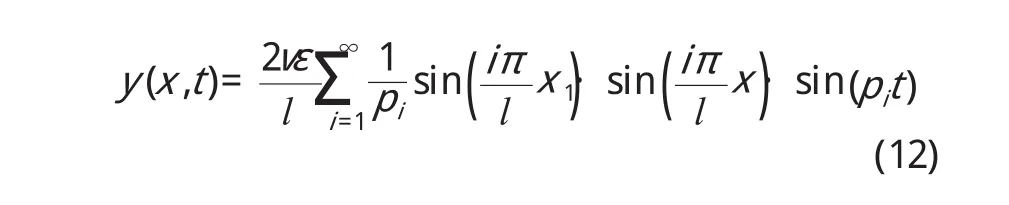
由于各階振型的幅值與i2成反比,故會有低階振型起主導作用,則在處的前三階振動響應為:
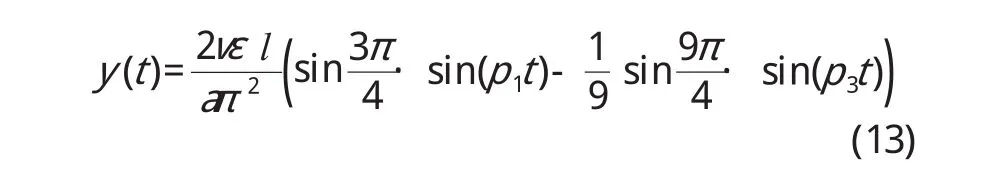
對于式(13),給定常數取值,其時域波形和各階主振動模式分別見圖3和圖4所示。
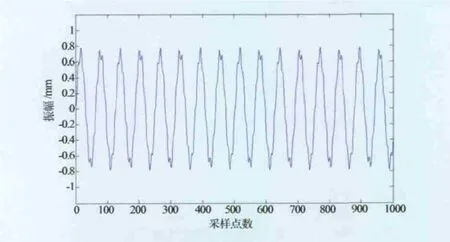
圖3 簡支梁振動響應時域波形
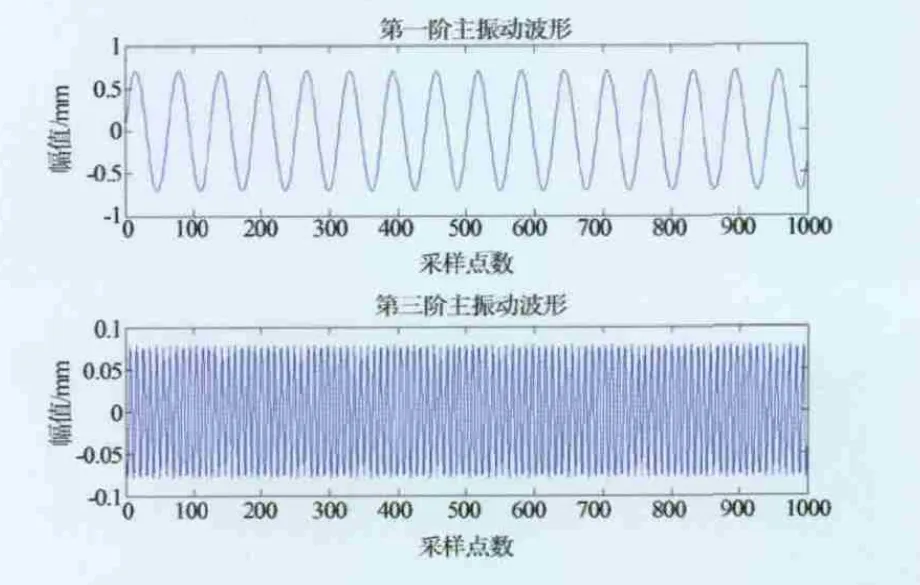
圖4 主振動組成
對圖3所示的簡支梁振動響應進行EMD分解,結果如圖5所示。
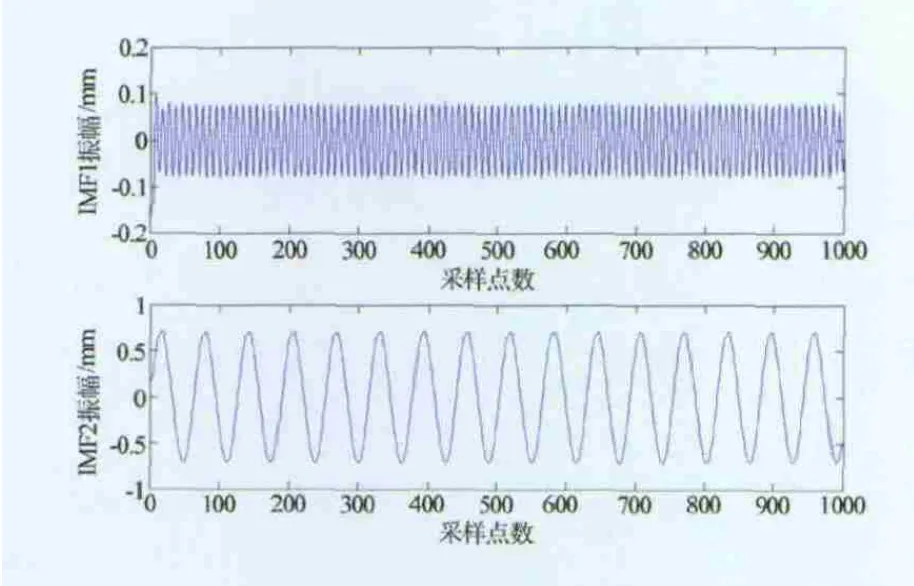
圖5 EMD分解結果
對比分析圖4和圖5,可清晰地看出經EMD分解的得到的IMF1對應了第三階主振動模式,IMF2對應了第一階主振動模式,分解結果中并沒有第二階主振動模式,這也與理論分析結果相一致。計算IMF1與第三階主振動模式和IMF2與第一階主振動模式的誤差及相關系數,結果分別見圖6和表1。
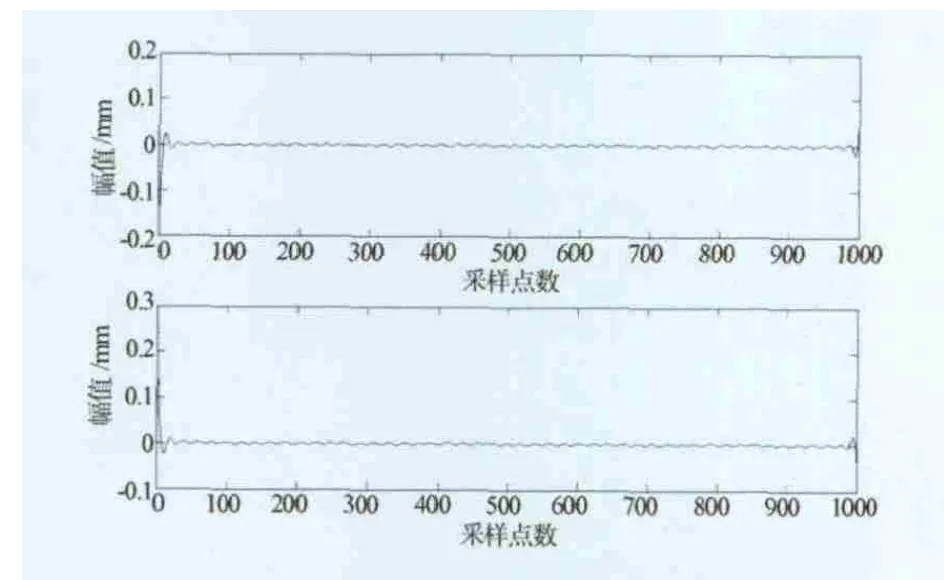
圖6 IMF與振動模式函數的誤差曲線
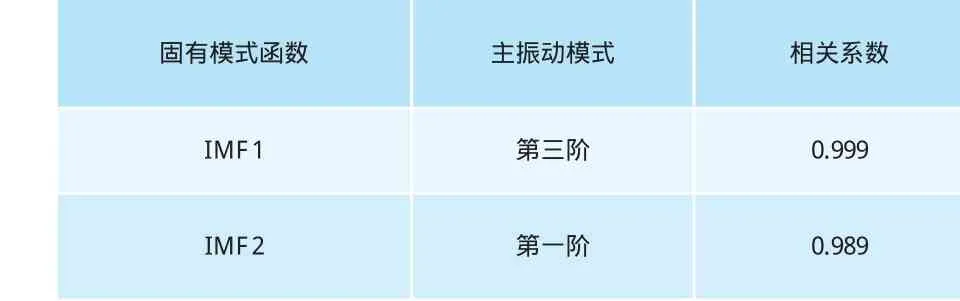
表1 IMF與振動模式函數之間的相關系數
從圖6中可見,固有模式函數與系統主振動模式函數之間的誤差很小,遠遠小于振動幅值。且從表1中的相關系數可見,固有模式函數與系統主振動模式函數之間的相關性接近于1。這說明,簡支梁的自由振動響應經EMD分解得到的固有模式函數與系統的主振動模式函數之間存在著物理對應關系。
4 簡支梁振動實驗
簡支梁振動實驗通過共振法激發簡支梁的各階振動模式,獲得對應的振動信號,驗證本文所提出的橋式起重機EMD模態分析方法的有效性。
如圖7所示為簡支梁振動實驗裝置的示意圖。激振器激發簡支梁振動,通過傳感器采集振動信號進入PC機分析[8-9]。該簡支梁參數為:l=60cm、b=5cm、h=0.8cm、E=2×105MPa。根據式(10)計算得到三階振動固有頻率分別為ω1=50.5Hz,ω2=201Hz,ω3=450Hz。
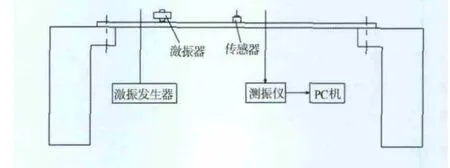
圖7 實驗裝置示意圖
調整激振頻率,使得簡支梁發生共振,測得一階共振信號和二階共振信號如圖8、圖9所示。將振動信號分別進行EMD分解,結果如圖10、圖11所示。
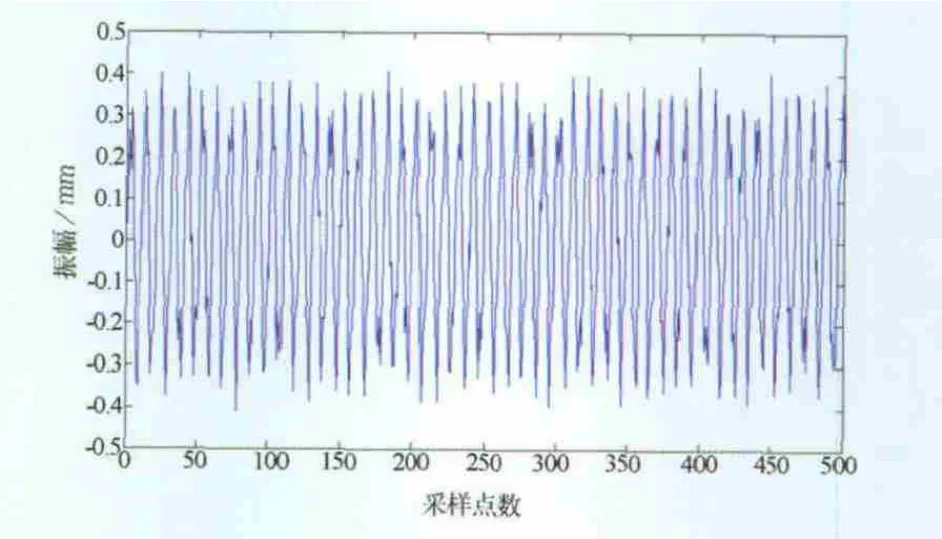
圖8 一階共振信號
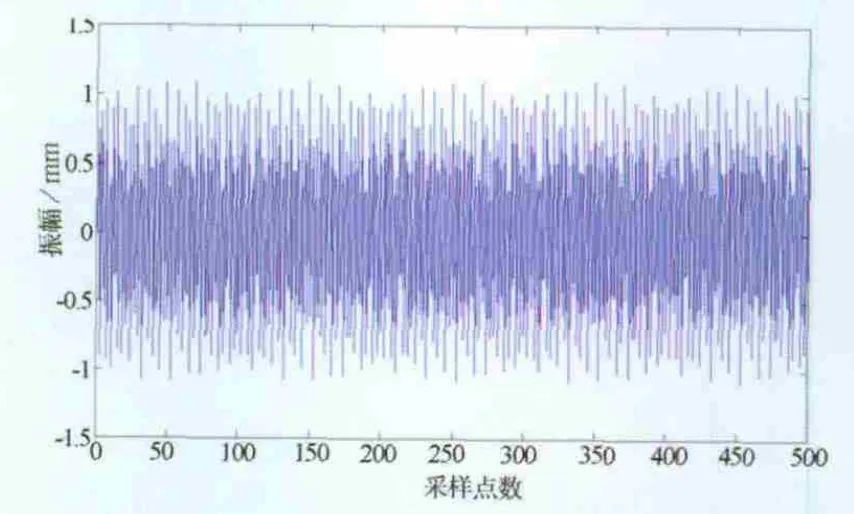
圖9 二階共振信號
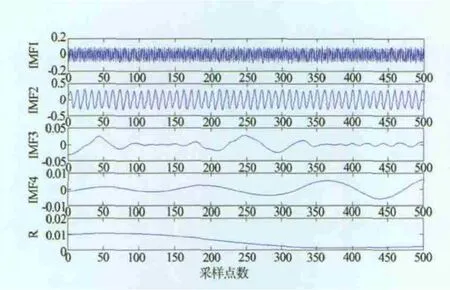
圖10 一階共振信號EMD分解
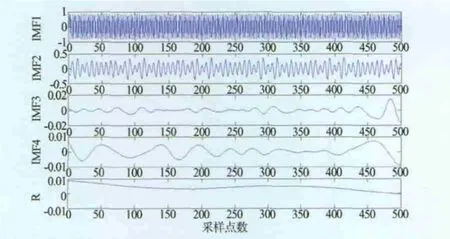
圖11 二階共振信號EMD分解
從圖10、圖11中可以看出IMF1與IMF2明顯是系統振動模式。分別計算一階、二階的IMF1與IMF2的傅氏譜,結果如圖12、圖13所示。可見一階和二階共振頻率包含于IMF1與IMF2的頻率成分中,且與理論計算值也較為吻合。
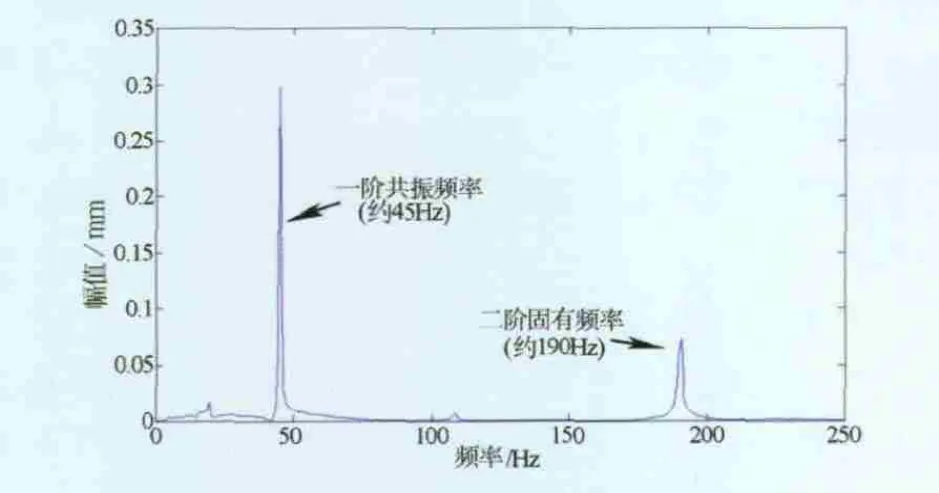
圖12 一階固有函數傅氏譜
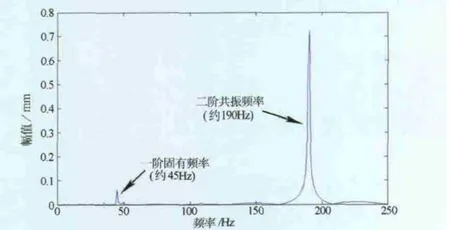
圖13 二階固有函數傅氏譜
實驗結果表明簡支梁振動信號經EMD分解得到的IMF和模態理論的振動模式之間保持較好的對應性,證實了橋式起重機EMD模態分析方法的可實現性。
5 結論
橋式起重機的振動模態分析是橋式起重機結構設計和制造的重要技術手段,將橋式起重機簡化為簡支梁模型,分析該模型的振動響應特性,應用EMD方法分析橋式起重機的振動信號,得到的IMF與振動模式之間有著高度的一致性。仿真分析與簡支梁振動實驗結果均表明基于EMD的橋式起重機振動模態分析是有效可靠的。
基于EMD的橋式起重機模態分析方法特別適用于在用、維修和改造的橋式起重機的模態分析,具有較高的分析準確性,為起重機的設計和安全運行提供參考依據。
1 楊明亮,徐格寧,常爭艷,晉民杰.基于有限元法的橋式起重機橋架模態分析.機械科學與技術,2012,31(1):135-137
2 張學良,王家營,連晉華.基于ANSYS的橋式起重機主梁模態分析.起重運輸機械,2007,(11):56-58
3 Norden E.Huang,S.Z.,Long SR.A new method for nonlinear and nonstationary time series analysis.4th international conference on stochastic structural dynamics,1999:559-564
4 李德葆,陸秋海.工程振動試驗分析.北京:清華大學出版社有限公司,2004
5 Kejian Guo,Xingang Zhang.Application of EMD method to friction signal processing. Mechanical System and Signal Processing,2008,20(1):248-259
6 曹沖鋒.基于EMD的機械振動分析與診斷方法研究.杭州:浙江大學,2009
7 J.D.Yau,Y.B.Yang.Vertical accelerations of simple beams due to successive loads traveling at resonant speeds.Journal of Sound and Vibration,2006,289,210-228
8 陳會蓮,池丹丹,張明.機械設備狀態監測虛擬儀器系統的研究.噪聲與振動控制,2009,29(3):47-49
9 姜忠宇,趙轉哲,畢海斌.簡支梁振動實驗臺載荷識別的測試.試驗技術與試驗機,2007,47(3):26-29

