基于空域加擾信號超平面特征的竊密算法

劉璐，金梁，黃開枝，鐘州

(國家數字交換系統工程技術研究中心，河南 鄭州 450002)

1 引言

無線通信技術在給人們帶來便利的同時，其信息安全問題也日益突出。傳統的無線保密通信主要是照搬有線通信中的密鑰體制，忽略了無線通信與有線通信的差異性。在無線通信系統中，不同用戶的接收信號是有差異的，這種差異使得在物理層實現保密通信成為了可能。

Wyner[1]首先提出在竊密信道(wiretap channel)中，僅依靠物理層的編碼即可實現保密通信，并且給出了保密容量的概念。Csiszár等人在文獻[2]中指出，對一般的高斯廣播信道，如果主信道容量大于竊聽信道容量時，系統保密容量大于零。然而實際中，竊聽者的方位信息一般未知，無法確定其信道狀態的優劣，若竊聽者的信噪比高于接收用戶，則無法保證通信的保密性。為了解決這一問題，Goel、Negi、Li等人從不同的角度分別提出了多天線保密通信的新方法[3～6]。這些方法的相同點可以概括為：發送端在主信道方向上發送信息波束，同時在其零空間發送人工噪聲。隨機加入的噪聲僅僅惡化竊聽方信號的接收質量，而合法用戶的正常通信不受影響，因而存在正的保密速率。這種利用空間方位的不同進行加密的方法，可統稱為空域加擾法[7]。

當竊聽者采用多天線接收時，Goel和Negi指出，人工噪聲會失效[4]，但沒有提出相應的竊密思路；Li在數學上證明了竊聽方無法通過盲解卷積的方法對空域加擾信號進行竊密[6]，但尚不清楚能否通過其他方式竊密。近幾年，關于空域加擾法的研究主要集中于優化信號與噪聲的功率分配[8,9]，以進一步提升保密速率。而相應的竊密算法研究較少。直到近期，吳飛龍等人提出了MUSIC-like竊密算法[7,10]，該算法利用信號子空間與噪聲子空間正交的特性，對有限字符集內所有可能出現的信號序列進行遍歷搜索，實現信息的獲取。該算法存在計算開銷過大的缺點。同時，受限于計算復雜度，其遍歷塊的長度往往較短，算法性能易受噪聲影響，因而很難在實際中應用。

針對這一問題，本文從空域加擾信號的信號空間角度出發，首先證明了發送天線數小于或等于竊聽天線數時，加擾信號呈現出平行的超平面分布特征，并指出這是多天線能夠竊密的根本原因。然后利用該特征，提出了一種超平面聚類算法，通過選取一組相互平行的超平面去逼近接收信號，利用樣本獲取超平面參數，進而破解信息。分析與仿真表明，該算法比MUSIC-like法在抗噪聲性能上提升了8～10 dB，計算復雜度低6～10個數量級，能夠用于實時解調。

2 系統模型

保密無線通信模型如圖1所示，發送端Alice向合法用戶Bob發送信息，遭到非法用戶Eve的竊聽。其中，Alice天線數用Na表示，Bob單天線，Eve天線數用Ne表示。

圖1 系統模型

窄帶通信系統中，Alice和Bob之間的主信道可以用向量hAB=[h1,h2,…,hNa]T表示，其中，hi為Alice的第i根發送天線到Bob接收天線之間的信道增益，上標T表示矩陣轉置。Alice到Eve的竊聽信道可以表示為一個Na×Ne的矩陣

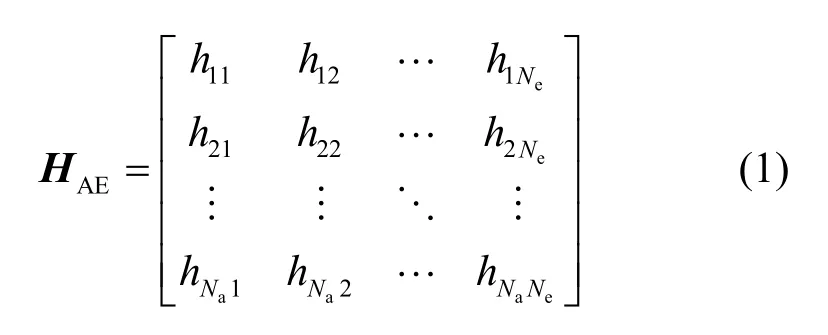
其中，hij為Alice的第i根發送天線到Eve的第j根接收天線之間的信道增益。假定所有信道都是慢衰落信道，信道增益在一個數據幀內保持不變，并且在不同幀之間獨立同分布。Alice在時刻n發送信號矢量x(n)，Bob和Eve接收到的信號分別為

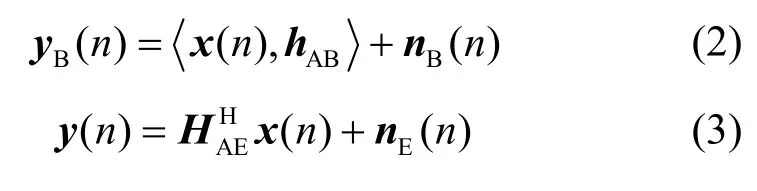
其中，nB(n)和nE(n)分別是n時刻Bob和Eve天線上接收到的加性高斯白噪聲表示酉空間的內積，上標H代表矩陣共軛轉置。

3 加擾信號的超平面特征

空域加擾的思想是Alice根據hAB對發送信息進行隨機映射，即利用多天線技術在主信道的零空間內對傳統的星座點進行高維展開。Bob首先發送訓練序列給Alice，Alice通過信道估計得到hAB。假定Alice的發送符號集為U={u1,u2,…,um}，其中m為發送符號集的大小。Alice在時刻n發送符號u(n)∈U，并用主信道單位方向對信息進行波束成型調制

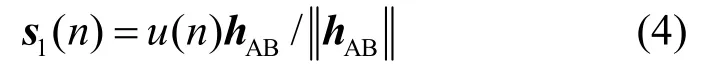
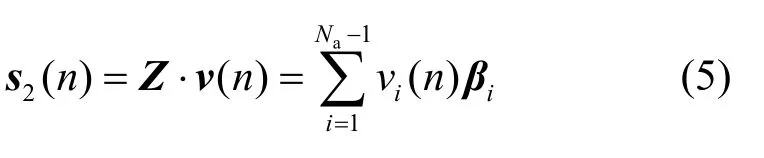
其中，v(n)=[v1(n),v2(n),…,vNa-1(n)]T為人工噪聲系數，是服從某種分布的隨機變量(一般假定其各元素獨立同分布，且服從復高斯分布)，并且與發送信息u(n)相互獨立；Z=[β1, β2,…, βNa-1]為hAB零空間的一組正交基，滿足＜ βi, hAB＞=0，i=1,2,…, Na-1。

Alice將調制信息同人工噪聲疊加后發送，即x(n)為

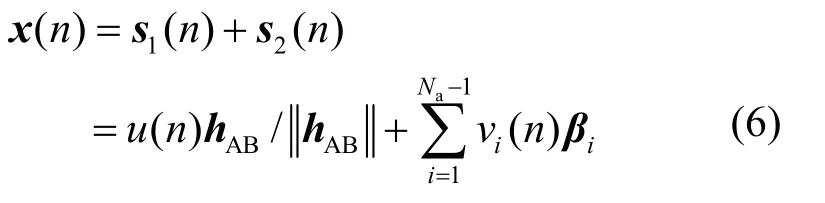
可見，x(n)是u(n),v1(n), v2(n),…, vNa-1(n)分別對主信道以及Na-1個零空間基向量進行調制疊加的結果。只有主信道方向攜帶信息，其他分量均為人工噪聲。

定理1 加擾信號x(n)的星座圖呈m張平行的超平面分布，每個超平面對應一個原始發送符號u(n)，主信道方向為超平面的法線方向，u(n)為超平面的偏移量。

證明 將x(n)向主信道投影，得到

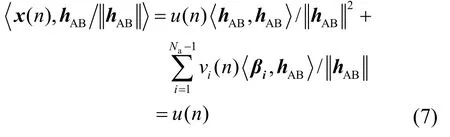
在幾何學中，集合H={x∈Cn|＜x, w＞}為n維酉空間中的一個超平面(hyperplane)[11]。其中，b∈C，被稱作H的偏移量；w∈Cn且|| w ||=1，被稱作H的法向量。可見，H被法向量和偏移量唯一決定，因此可以用(w,b)來簡化表示H，其幾何意義如圖2所示，代表在w方向上投影為b的點組成的集合。當且僅當H1∩H2=?時，稱超平面H1與H2相互平行，記作H1//H2。

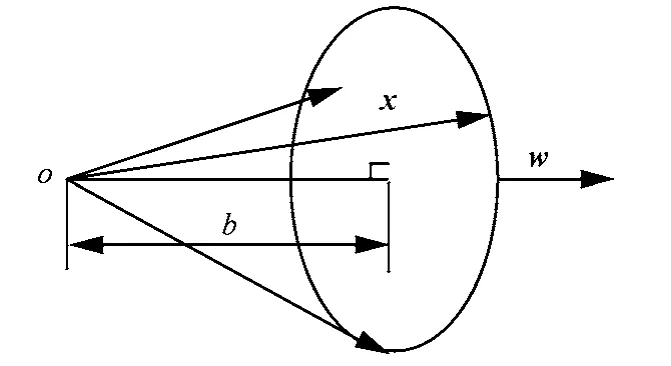
圖2 超平面示意

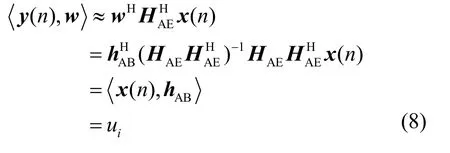
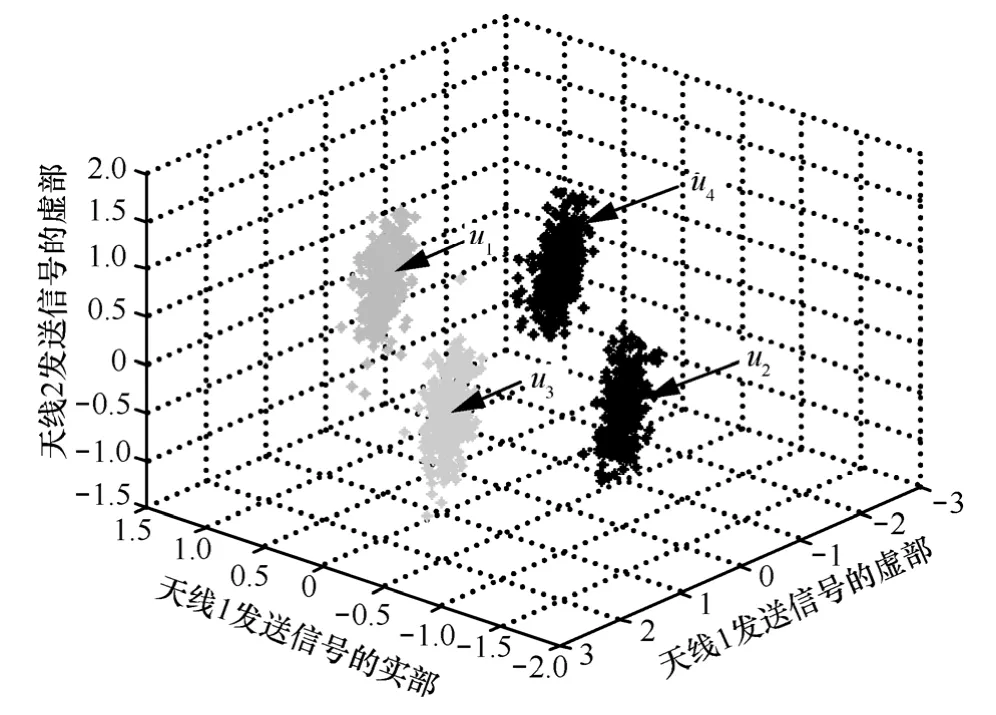
圖3 加擾信號星座圖的超平面分布(2根發送天線，QPSK調制)

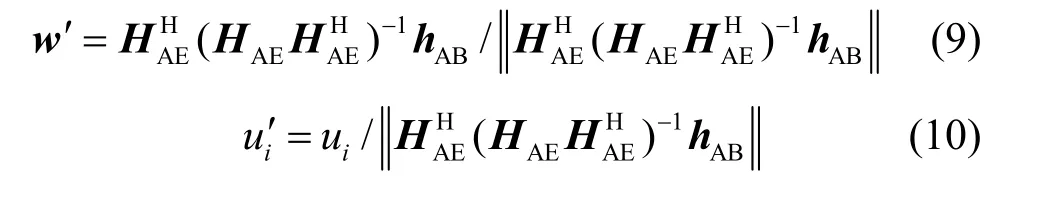
定理1從幾何的角度揭示了空域加擾的本質，雖然它隨機置亂了發送星座圖，但為了讓Bob能夠常規解調，置亂的信號依然需要服從一定的規則，即星座點只能在相應的超平面內隨機置亂。定理2解釋了空域加擾法在Ne≥Na時失去保密性的根本原因：當竊聽天線數目充分多時，Eve相當于在另一組基下觀測加擾信號，而空間超平面的幾何關系具有旋轉和平移的不變性，并不會隨基的變化而改變。所以超平面特征是Eve截獲信息的突破口。

4 超平面聚類竊密算法

基于加擾信號的上述幾何特征，設計超平面聚類法(HC, hyperplane clustering)進行竊密。該算法利用m張平行的超平面對一幀內前K個接收信號y1, y2,…,yK進行聚類，得到最佳超平面參數w?和如圖4所示，Eve利用所得到的參數，對該幀信號進行解調。

設dij為yi到Hj的距離的平方，即

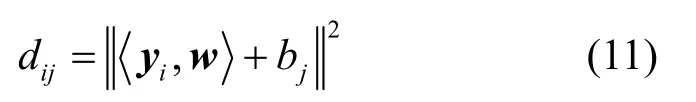
建立目標函數為

圖4 竊密解調器

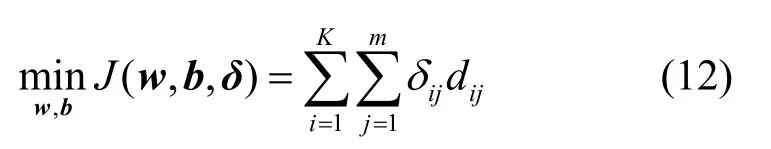
其中，b=(b1,b2,…,bm)T代表m張超平面的偏移量；w是共同的法向量；布爾矩陣δ=(δij)K×m滿足

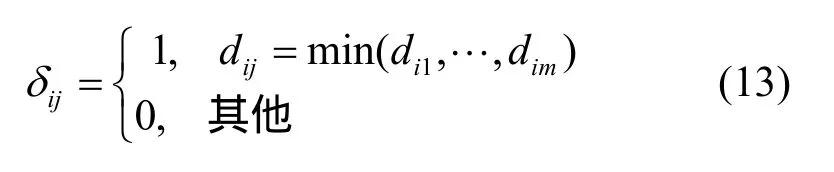
即用m張平行的超平面去逼近K個接收信號樣本點，且“逼近效果”用各點離超平面最小距離的平方誤差之和來衡量。采用如下的方法對式(12)迭代求解。

1) 0n=，并隨機初始化(0)w和(0)b。

3) 最優化w和b，并重新劃分超平面。即在式(12)中，對w和b分別求偏導，并令導數為零（詳細計算過程見附錄），可得

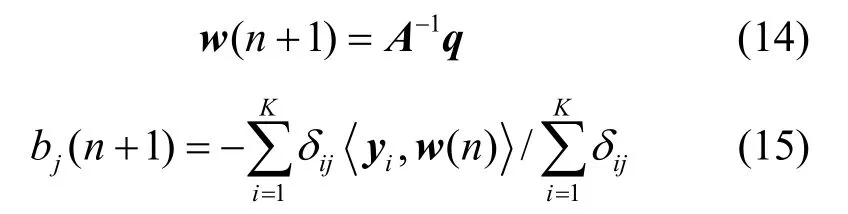
其中，A為對稱矩陣，且

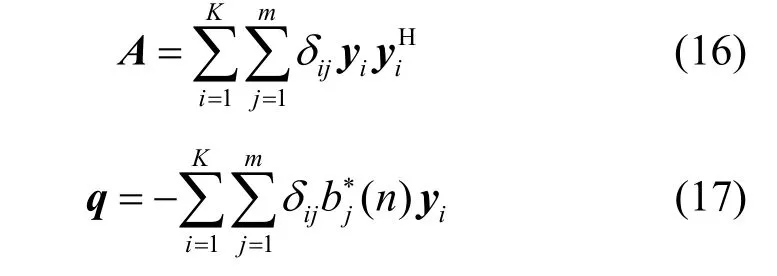
4) n=n+1，重復步驟2)和步驟3)，直至w和b收斂到

5 性能仿真和復雜度分析

本節仿真驗證所提算法，討論參數：Ne、K、Eve接收信噪比SNR以及信干擾比SIR(Alice信息發送功率與干擾發送功率的比值，SIR越小，干擾功率越大)對竊聽BER(誤比特率)的影響。并且在相同條件下，將超平面聚類法(HC)的BER以及計算復雜度同現有的MUSIC-like法進行比較。

5.1 性能仿真

性能仿真參數如表1所示。

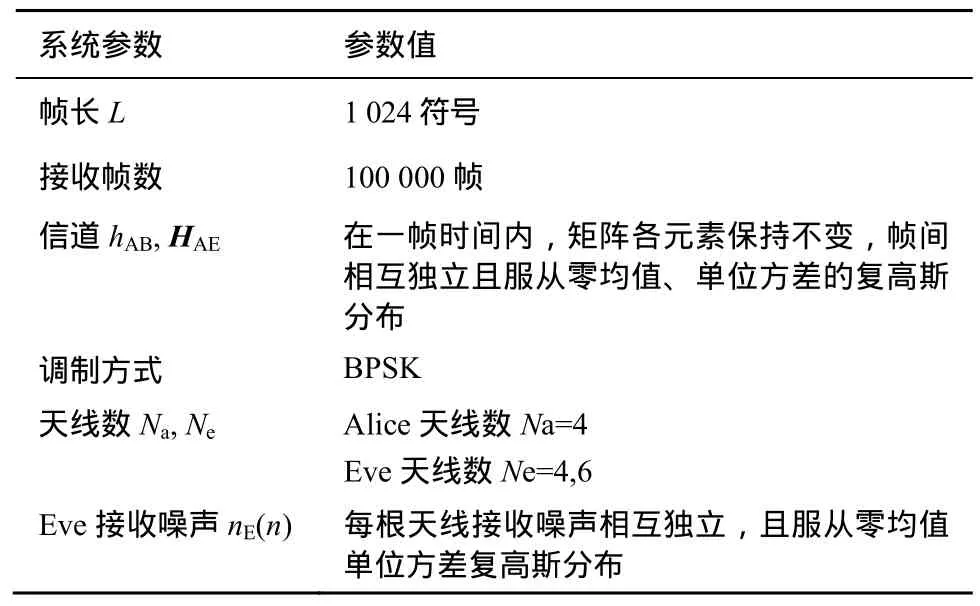
表1 仿真參數

1) 聚類樣本點個數K的影響

由于竊聽方無法獲取訓練樣本，只能通過盲辨識途徑截獲信息，因此需要利用較多的接收樣本點（該樣本點所攜帶的具體信息未知）校正超平面參數。從幾何角度看，只有接收信號足夠多時，其超平面分布的特征才會更加明顯。如圖5所示，開始時，BER大幅下降，但K增大到一定程度后，BER不再顯著變化。因此，綜合考慮竊密性能和計算復雜度，樣本數無需過大，下面仿真中均取K=200。

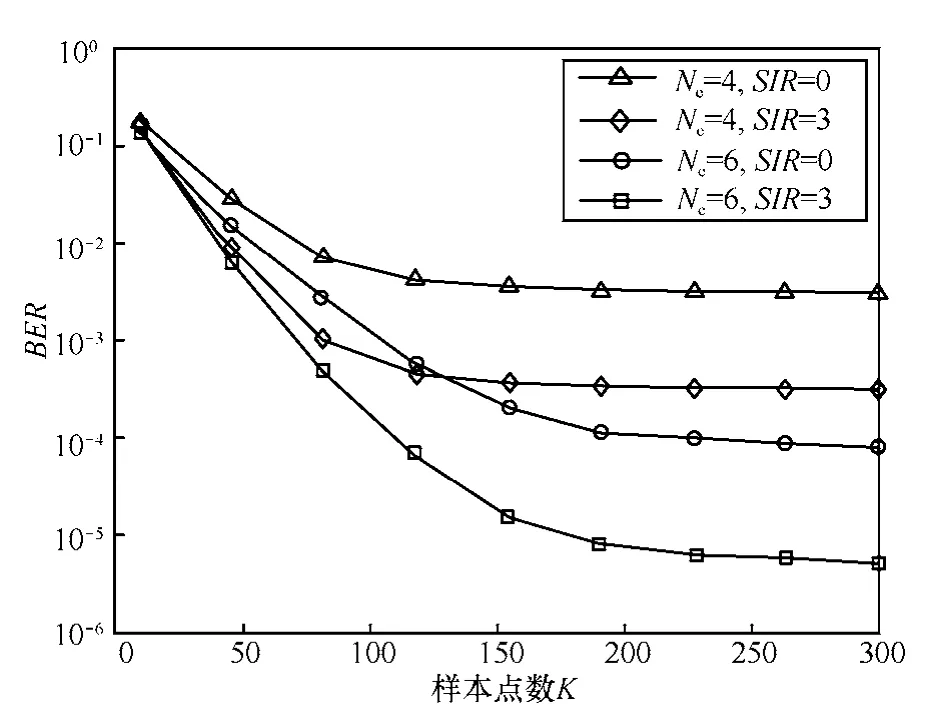
圖5 聚類樣本個數K對算法性能的影響(SNR=10 dB)

2) 算法收斂性

將式(9)和式(10)所示的理論值與HC所獲得的估計值進行對比，分別在大小信噪比下驗證算法的收斂性。結果如圖6所示，其中，用向量夾角衡量和w的誤差，用衡量偏移量誤差。可見，算法收斂速度較快，且在大信噪比下能夠逼近實際值，同時，算法收斂性隨天線數增大而改善。

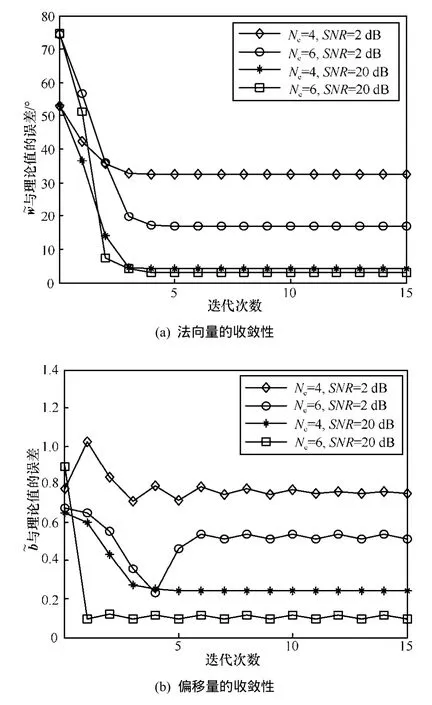
圖6 算法的收斂性(SIR=0 dB)

3) 抗噪聲性能

在Alice采用相同功率發送干擾和信息的條件下，Eve的信息截獲性能如圖7所示。同MUSIC-like算法相比(設其遍歷塊長度 ?9K=)，HC法的BER曲線向左平移了約8～10 dB。原因分為兩方面：從MUSIC-like方法來說，其計算復雜度隨?K呈指數增長，所以?K的取值不能太大(通常取6～9，遠小于K)，無法充分利用樣本信息，易受信道噪聲影響；從HC算法來說，向法向量w做投影的過程，不僅保留了信息成分、抵消了人工噪聲，同時也消除了信號空間中其他方向上的噪聲。所以，HC的抗噪性優于MUSIC-like算法。

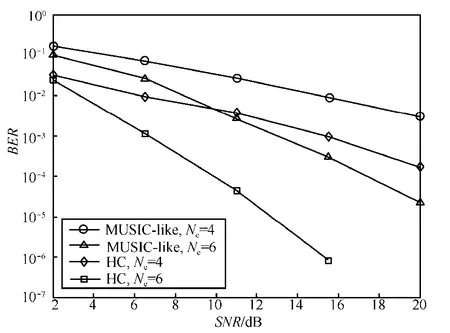
圖7 竊密算法的BER性能(SIR=0 dB)

4) 信干擾比的影響

信干擾比對算法解調性能的影響如圖8所示。隨著SIR的提升，HC法的誤碼率急劇下降。這是因為SIR越大，超平面間距越大，相應聚類效果就會越好。然而，MUSIC-like法沒有利用該特征，性能提升較小。

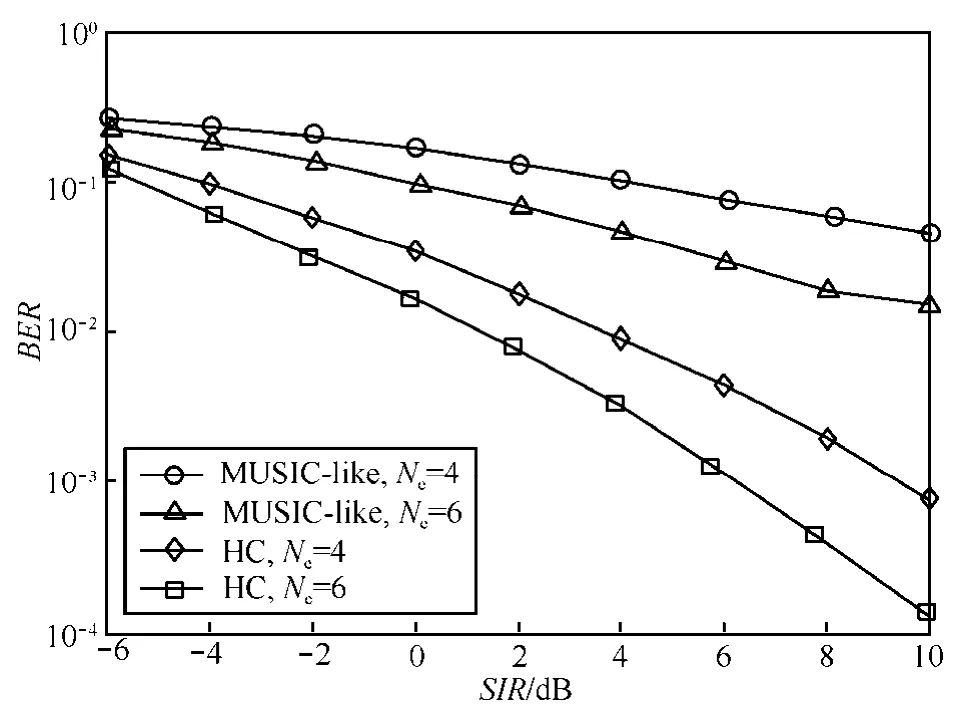
圖8 SIR對算法性能的影響(SNR=2 dB)

5.2 計算復雜度分析

HC法利用了超平面特征對信號建模分類，其計算復雜度主要集中于算法的第2步，需要乘累加個數約為O(mKNe)。得到和后，解調一幀符號所消耗的乘累加數約為O(LNe)。因此，共需消耗乘累加數約為O(TmKNe+LNe)，其中，T為迭代次數；而同樣條件下，由于需要遍歷符號集，MUSIC-like 法計算復雜度較高，消耗乘累加數約為

為了直觀地對比2種算法的計算量，假設Alice采用表2所示的物理層參數（為3GPP2推薦的標準物理層格式[12]）發送加擾信號，Eve實時解調所需處理速度如圖9所示。可見MUSIC-like法所需的處理速度大大超出常規DSP器件的處理速度（約1 000億次乘加運算/秒，MMAC）。而HC法比MUSIC-like法的計算復雜度下降了6～10個數量級，目前DSP器件的運算速度能夠滿足其實時處理的需求。

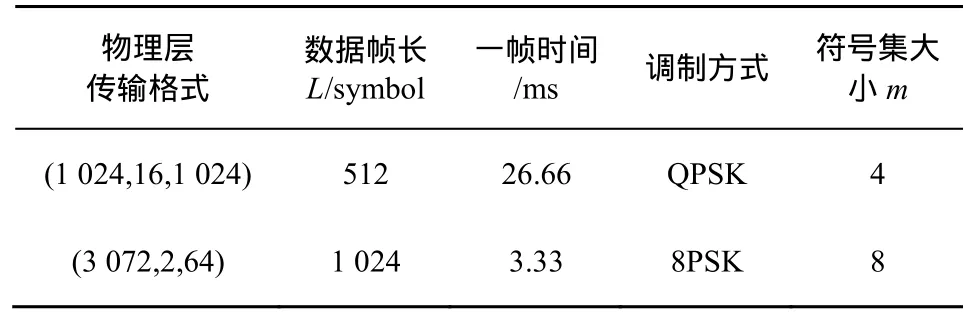
表2 物理層幀格式

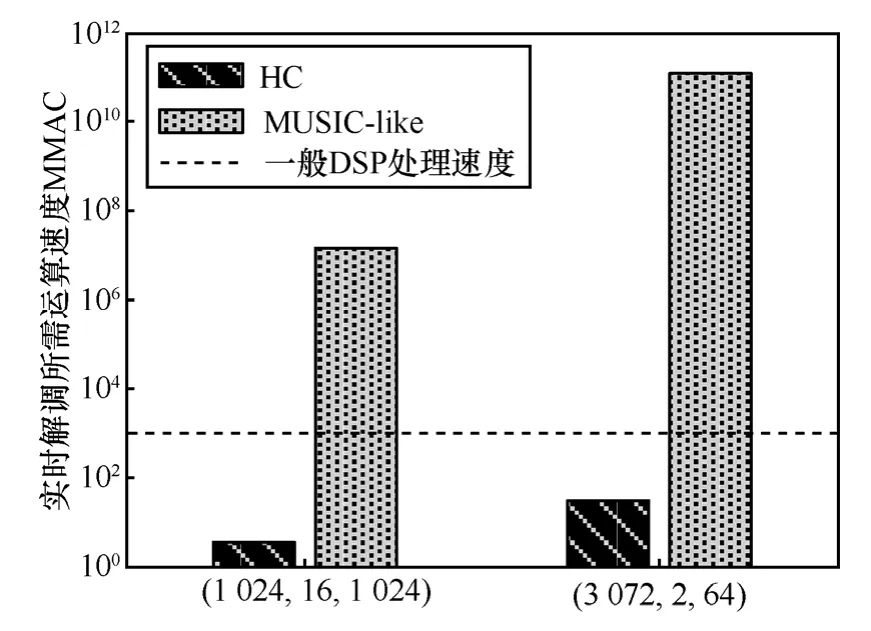
圖9 實時解調所需運算速度

6 結束語

在文獻[7]的研究基礎之上，本文對空域加擾法做了更為深入的分析，從幾何角度入手，指出了竊密的可行性在于加擾信號存在超平面分布特征，并據此設計了超平面聚類算法，完成信息截獲。HC法比現有的MUSIC-like算法抗噪性能好，計算復雜度低，便于實際應用。若要利用空域加擾法實現保密通信，一方面要縮短幀長來隱藏超平面特征；另一方面也可以優化加擾圖案，零空間內的高斯白噪聲能被多天線分離，并不具有隱蔽性，反而容易暴露超平面特征。如何設計具有信息隱蔽性的加擾圖案，值得進一步研究。

附錄 式(14)和式(15)的證明

設復向量a, x∈Cn，b∈C，令y=xHa+b ，為了方便對x的實部和虛部分別求偏導，可將n維復向量看作2n維實向量進行處理：

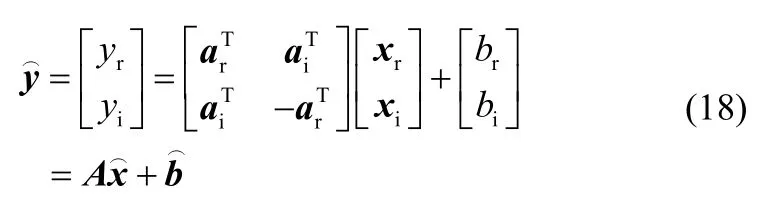
其中，下標r和i分別代表相應變量的實部和虛部，即x=xr+j xi，a=ar+jai，y=yr+jyi，b=br+jbi，并且

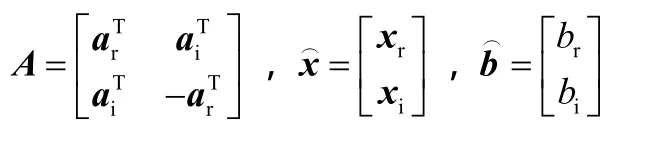
式(18)中的元素均為實數，而

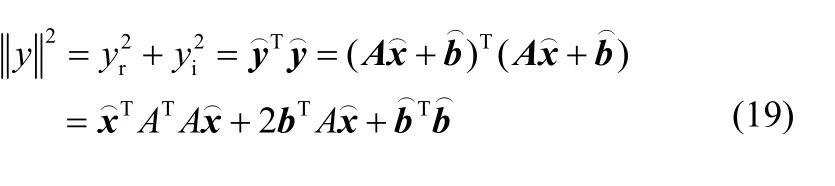
所以利用實數求導公式可以得到

令偏導為零，可得

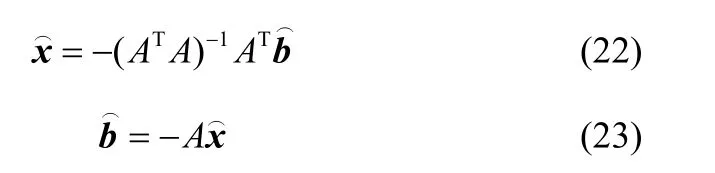
將式(22)和式(23)轉換成相應的復數形式，即

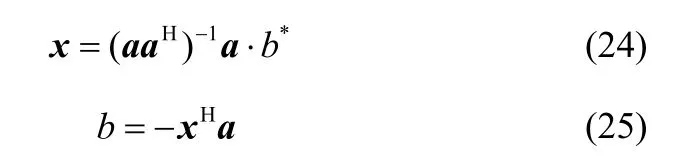
將式(24)、式(25)代入對式(12)的求導過程中，即可得到式(14)、式(15)。

[1] WYNER A D. The wire-tap channel[J]. Bell System Technical Journal,1975, 54(8): 1355-1387.

[2] CSISZáR I, K?RNER J. Broadcast channels with confidential messages[J]. IEEE Transactions on Information Theory, 1978, 24(3): 339-348.

[3] NEGI R, GOEL S. Secret communications using artificial noise[A].IEEE Vehicular Technology Conference[C]. Dallas, USA, 2005.1906-1910.

[4] GOEL S, NEGI R. Guaranteeing secrecy using artificial noise[J].IEEE Transactions on Wireless Communications, 2008, 7(6): 2180-2189.

[5] LI X, HWU J, RATAZZI E P. Array redundancy and diversity for wireless transmissions with low probability of interception[A]. IEEE International Conference on Acoustics, Speech and Signal Processing[C]. Toulouse, France, 2006.211-221.

[6] LI X, HWU J, RATAZZI E P. Using antenna array redundancy and channel diversity for secure wireless transmissions[J]. Journal of Communications, 2007, 2(3): 224-232.

[7] 吳飛龍, 王文杰, 王慧明等. 基于空域加擾的保密無線通信統一數學模型及其竊密方法[J]. 中國科學, 2012, 42(4): 483-492.WU F L, WANG W J, WANG H M,etal. A unified mathematical model for spatial scrambling based secure wireless communication and its wiretap method[J]. Science China, 2012, 42(4): 483-492.

[8] ZHOU X, MCKAY M R. Secure transmission with artificial noise over fading channels: achievable rate and optimal power allocation[J].IEEE Transactions on Vehicular Technology, 2010, 59(8): 3831-3842.

[9] YANG Y C, WANG W, HUI Z. Transmitter beamforming and artificial noise with delayed feedback: secrecy rate and power allocation[J]. IEEE Journal on Communications and Networks, 2012, 14(4): 374-384.

[10] LI H, WANG W J, YIN Q Y. A MUSIC-like blind co-channel signals separation algorithm and its performance analysis, circuits and systems[A]. IEEE International Symposium on Circuits and Systems[C].Taipei, China, 2009. 844-847.

[11] LUENBERGER D. Optimization by Vector Space Methods[M]. New York: Wiley, 1969.

[12] 3GPP2 C. S0024-A, cdma2000 High Rate Packet Data Air Interface Specification-part 13: SUBTYPE 2 Physical Layer-Modulation Characteristics[S]. 2006.