黏彈阻尼對一維桿狀聲子晶體能帶結構頻移的影響

張思文,吳九匯,劉彰宜

(1.西安交通大學機械工程學院, 710049, 西安;2.西安交通大學機械結構強度與振動國家重點實驗室, 710049, 西安)

黏彈阻尼對一維桿狀聲子晶體能帶結構頻移的影響

張思文1,2,吳九匯1,2,劉彰宜1,2

(1.西安交通大學機械工程學院, 710049, 西安;2.西安交通大學機械結構強度與振動國家重點實驗室, 710049, 西安)

為了明確黏彈阻尼對聲子晶體能帶結構的影響,根據黏彈材料的標準線性固體模型,利用平面波展開法的迭代算法對一維黏彈材料聲子晶體的能帶結構進行了理論計算和對比分析。與彈性模量為常數的完全彈性材料相比,黏彈材料由于其復模量的頻率相關性,儲能模量和損耗模量對聲子晶體的能帶結構都有重要影響,特別是損耗模量對聲子晶體能帶結構的影響在阻尼峰值附近的頻率范圍不容忽視。位于此頻率范圍的能帶被調向更高頻而其他范圍的能帶基本不變,從而使能帶下方帶隙增寬而上方帶隙變窄。損耗模量對能帶結構的這一特定調節作用為黏彈性阻尼材料應用于聲子晶體提供了一定的理論基礎,也為獲得寬頻帶隙提供了一種新的方法。

聲子晶體;能帶結構;黏彈材料;阻尼;帶隙特性

聲子晶體是一種彈性散射體周期排列形成的新型人工周期性功能材料,由于其具有優越的控制彈性波傳播的能力,受到了廣泛的關注和研究,并在減振降噪等方面具有潛在的應用前景。Rayleigh早在1887年就已指出,連續周期結構中存在無波傳播模式的頻率范圍。彈性波或聲波在聲子晶體結構中傳播時,受到內部周期結構的作用,一些頻率范圍的彈性波無法通過結構向前傳播,稱為禁帶或帶隙[1]。直到20世紀90年代,對于聲子晶體才開始有比較廣泛的研究[2-5]。對于聲子晶體的初期研究主要側重于帶隙的產生機理和計算方法,并分析影響帶隙頻率范圍的主要因素(包括材料、晶格常數、填充率等)[6-8]。計算聲子晶體能帶結構(即色散關系曲線)的主要方法有傳遞矩陣法、平面波展開法[6]、時域有限差分法[7]、多重散射法[8]、集中質量法及有限元法等。組成聲子晶體結構的可以是固體,也可以是流體。平面波展開法是最常用的算法之一,在計算固-固型、流-流型聲子晶體的能帶結構時相當成功,但在計算組元材料參數差異較大的固-流型聲子晶體時存在一定的困難,收斂較慢[1]。前期對于聲子晶體的研究,很少考慮到組元材料的阻尼(如流體的黏滯阻尼、固體的黏彈阻尼)對能帶結構和帶隙特性的影響。2000年前后,一些學者研究了流體的黏滯阻尼對固-流型聲子晶體帶隙特性的影響,指出:當聲子晶體結構的特征長度與流體的黏性穿透深度相當時,流體黏滯阻尼對帶隙有重大影響[9-10]。

黏彈材料是同時具有流體黏性和固體彈性的材料,如塑料、橡膠等聚合物,陶瓷,混凝土等[11]。在彈性材料中,彈性模量為實數且與頻率無關,而對于黏彈性材料,彈性模量不僅為復數,而且是頻率的函數。將黏彈材料應用于聲子晶體周期結構,使得能帶結構的計算復雜化,但其對于帶隙特性的調節作用吸引了不少學者的研究[12-22]。在處理黏彈材料時,一些學者將其視為具有特定阻尼的彈性材料而沒有考慮阻尼和彈性常數隨頻率的變化[12-14];一些學者用復數來表示彈性模量,并認為其虛部(即損耗模量)只表征為對能量的耗散,而決定彈性波傳播行為(如色散關系)的是其實部(即儲能模量),因此只考慮儲能模量對聲子晶體色散關系的影響[15-19]。王剛、溫激鴻等人還對比了理論計算和實驗測試的結果,認為黏彈阻尼不改變結構的色散關系,只表現為對高頻能量的耗散作用,從而增大了帶隙的寬度[15-16]。Zhao等人給出了黏彈材料的復模量模型,但在計算由其組成的聲子晶體的色散關系時,仍然只考慮了儲能模量的影響[18-19]。上述研究中認為損耗模量只表現為對能量的耗散而對色散關系沒有影響是缺乏理論依據的,也沒有文獻對此進行過討論,因此其合理性還有待商榷。Merheb等人同時考慮了材料黏彈性對聲子晶體結構色散關系和耗散的影響[20-22]。然而,他們雖然指出了黏彈阻尼對聲子晶體能帶結構有重要影響作用,但都沒有深入討論在整個頻率范圍,特別是跨過阻尼峰前后,損耗模量對聲子晶體能帶結構頻移的貢獻。

本文根據標準線性固體模型,研究了材料黏彈性對聲子晶體能帶結構的影響,分析和討論了損耗模量對能帶結構的頻移影響。利用平面波展開法的迭代算法對含有黏彈材料的一維聲子晶體能帶結構進行了理論計算,對比分析了將彈性模量視為常數、只考慮儲能模量、同時考慮儲能模量和損耗模量這3種情況下的帶隙特性,發現了損耗模量對能帶的特定調節作用,并進一步討論和分析了這一特定調節作用的機理。

1 黏彈性材料模型及其頻率相關性

彈性波在黏彈性介質中傳播時,應力和應變響應之間存在一定的相位差,表示應力-應變關系的彈性模量可以表示為復模量形式[11]

E*(iω)=E′(ω)+iE″(ω)=E′(ω)(1+iβ(ω))

(1)

式中:E′(ω)為儲能模量,它與存儲在材料中的彈性勢能有關;E″(ω)為損耗模量,它與耗散在材料中的能量有關;損耗因子

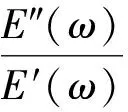
(2)

其中δ為損耗角,也是應變滯后于應力的相位差。

對于黏彈材料,儲能模量、損耗模量及損耗因子都是頻率的函數。它們并不是相互獨立的,而是滿足Kramers-Kronig關系[23]。標準線性固體模型(如圖1a所示)是常用于描述黏彈材料力學特性并滿足Kramers-Kronig關系的經典模型,其復模量表示為

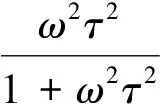
(3)

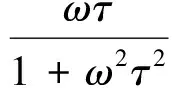
(4)

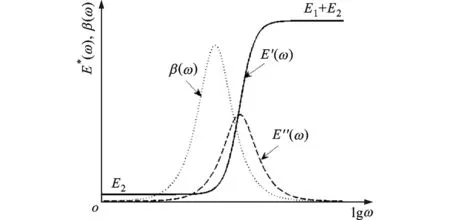
式中:E2、E1+E2分別為極限頻率下的模量值;τ為松弛時間,τ=η/E1,η為黏性元件的黏性系數,它們都由具體材料確定。將復模量及損耗因子表示在同一坐標中,如圖1b所示。

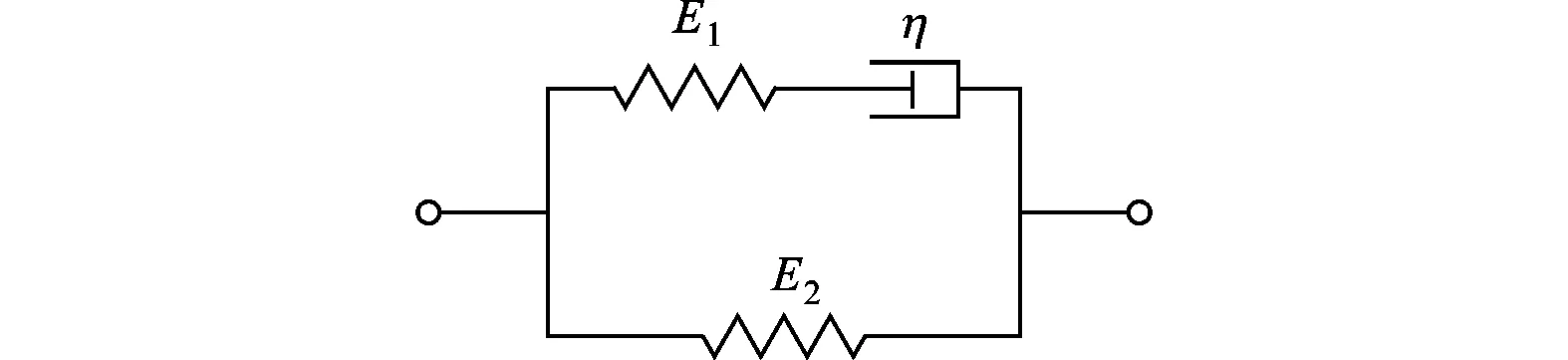
(a)標準線性固體模型

(b)復模量對頻率的依賴關系

對比圖1a中的材料模型和圖1b中復模量隨頻率的變化曲線可知,由于黏性元件所承受的力與應變速率密切相關,模型的兩個分支之間的耦合作用也隨頻率改變,使得該模型具有如下頻率特性:①在低頻范圍,由于應變速率極小,黏性元件基本上不產生阻力,使得由黏性元件和彈性元件E1組成的分支被隔離,此時相當于完全彈性材料,彈性模量為E2,并且基本不隨頻率變化;②當頻率增大時,應變速率隨之增大,黏性元件承受的作用力也增大,一方面E1不斷并入模型中,使儲能模量增大,另一方面能量也不斷損耗在黏性元件中,損耗模量也隨之增大;③在高頻范圍,應變速率很大,黏性元件跟不上應變的變化,E1完全并入模型中,儲能模量也趨于一個較大的恒定值,而損耗模量逐漸減小為0。

損耗模量隨著頻率的升高先增大后減小,在一定頻率范圍內達到最大值,稱為黏彈材料的阻尼峰,如圖1b所示。材料的這些頻率特性將直接影響由其組成的聲子晶體的能帶結構及其帶隙特性。

2 一維聲子晶體能帶結構的計算方法

aA,aB: A、B 2種材料的寬度

在標準線性固體模型的基礎上,利用平面波展開法的迭代算法計算并分析黏彈阻尼對一維聲子晶體能帶結構的影響。圖2為A、B 2種材料組元交替排列形成的一維桿狀聲子晶體結構的示意圖,其中晶格常數a=aA+aB。平面波展開法是計算聲子晶體能帶結構常用的方法,計算時考慮的是無限周期的理想結構,而當引入黏彈性時,特征值問題變得難以求解,因此本文采用迭代算法來計算。

一維桿狀聲子晶體結構中的彈性波滿足如下波動方程

(5)

式中:ρ(x)、E(x)分別為材料密度和彈性模量;u(x,t)為截面沿x方向的位移。對于結構中的諧波,根據Bloch定理,式(4)解的形式可以寫為

u(x,t)=uk(x)e(kx-ω t)

(6)

式中:k為波矢。由于結構的周期性,波幅uk(x)與材料參數ρ(x)、E(x)(對于黏彈性材料,E(x)為復數并為頻率的函數,應寫作E*(x,ω))具有相同的空間周期性,可以同時按傅里葉級數形式展開后代入式(5),經整理求解可得考慮材料黏彈性的一維桿狀聲子晶體特征頻率的無限階方程[15-16,20]

(7)

式中:ω為圓頻率;G0、G′為倒格矢,在整個倒空間取值。為了求得方程的數值解,G0、G′通常在有限倒空間取值,式(7)即變為有限階方程。給定k可以求得一系列特征頻率值;讓k在倒空間取遍第一布里淵區(-π/a,π/a),即可求得一維桿狀聲子晶體的能帶結構。

對于一般彈性材料組成的聲子晶體結構,彈性模量不隨頻率變化,式(7)即退化為一般的特征值問題。在Matlab中只需要構建特征矩陣,利用eig函數就可以求得方程的特征值。當引入材料黏彈性后,彈性模量變為復數并且是頻率的函數,此時在Matlab中方程的數值解不能簡單用上述函數來求取,而只能通過迭代算法來求取。在求解給定k下的某一階特征頻率時,先設定一個參考頻率ωr,根據黏彈性材料模型計算出復模量E*(ωr),然后按照上述方法求解出特征頻率。將特征頻率與參考頻率ωr進行對比,當它們之間的差值小于設定容差即可;否則,更新參考頻率并繼續迭代。這樣迭代下去,對應每一個給定的k就可以得到一系列的特征頻率,從而可以繪制以波矢(一般除以π/a,使其在0～1之間變化)為橫坐標、頻率為縱坐標的能帶結構圖。

3 復模量對能帶結構頻移的影響

對于由一般完全彈性材料組成的聲子晶體,彈性模量都視為常數,不同組元之間的密度和彈性模量相差得越大就越容易產生帶隙。對于含有黏彈性材料的聲子晶體結構,彈性模量不僅為復數,而且隨頻率變化。在研究材料黏彈性對聲子晶體能帶結構的影響時,文獻[15-19]都忽略了損耗模量的影響,只考慮了儲能模量的影響,而文獻[20-22]則指出,損耗模量對能帶結構具有重要影響。

對由金屬材料(不考慮黏彈性)和黏彈性橡膠交替排列組成的一維聲子晶體桿結構的能帶結構進行了計算,通過對比分別分析了儲能模量和損耗模量對能帶結構的影響。在計算中,取晶格常數a為0.1 m,組元寬度比例為1∶1。金屬材料的密度ρA為7 890 kg/m3,彈性模量EA為196 GPa。黏彈性材料的密度ρB為1 300 kg/m3,模量參數E1為60 MPa,E2為2 MPa。圖3繪出了不同松弛時間時黏彈性材料的復模量隨頻率變化的曲線。從圖中可知,松弛時間決定阻尼峰的中心頻率。為了探討損耗模量對聲子晶體能帶結構的影響,當τ=10-4s時,對以下3種情況的能帶結構進行了對比:①彈性模量為實常數(在所計算的頻率范圍求取的平均值EC=30 MPa)的情況;②儲能模量按圖1b所示隨頻率變化,而忽略損耗模量影響的情況;③儲能模量和損耗模量都隨頻率變化的實際情況。前3階能帶結構的對比結果如圖4所示。

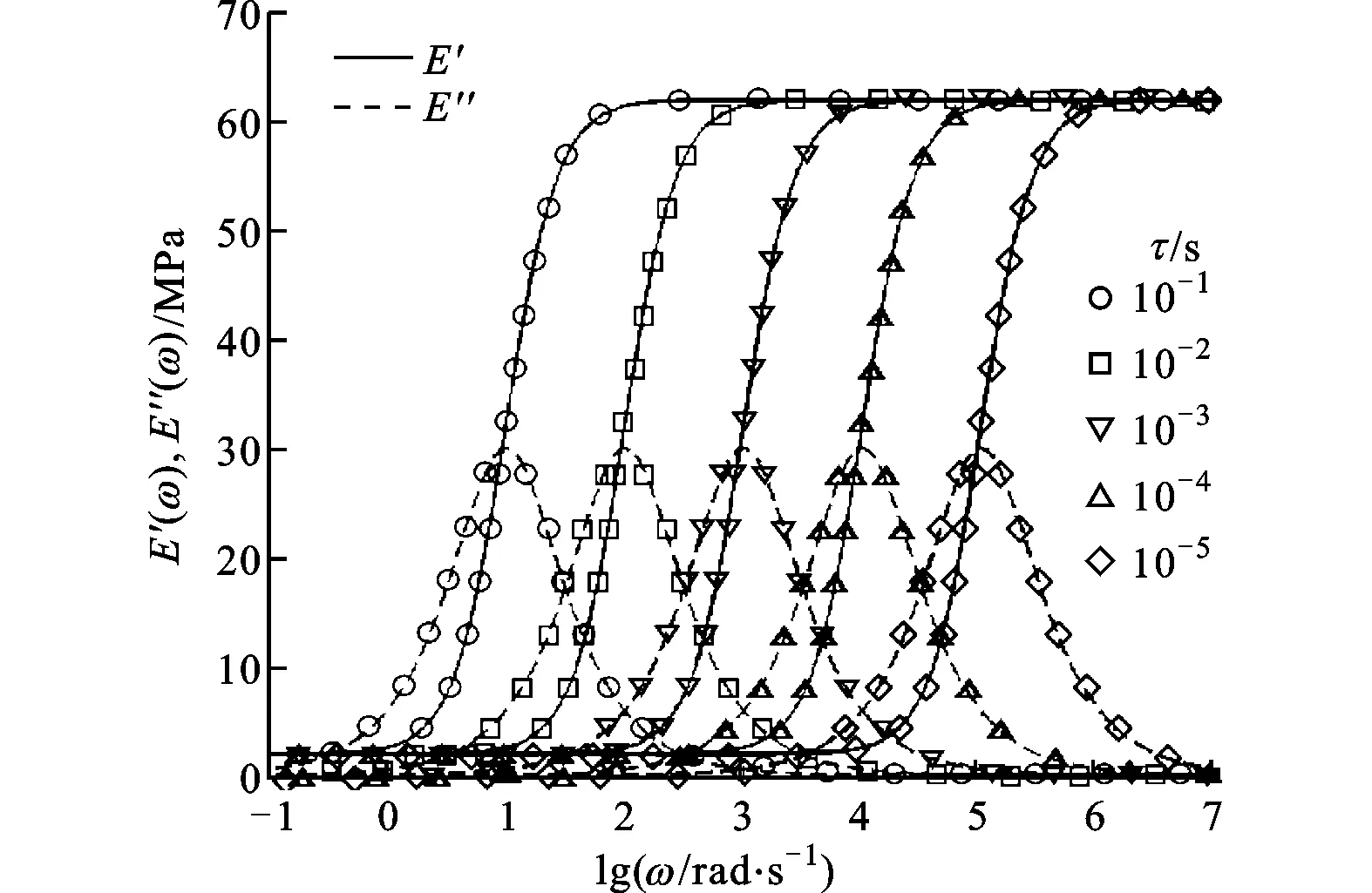
圖3 不同松弛時間下復模量隨頻率的變化曲線

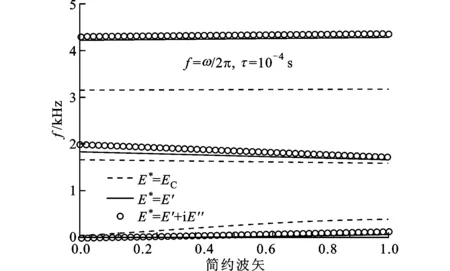
圖4 復模量對聲子晶體能帶結構的影響曲線

從圖4中可以看出,彈性模量為復數時所得到的聲子晶體能帶結構與彈性模量視為常數的情況相差很大,各階能帶之間形成的帶隙也增寬了很多。考慮材料的黏彈性,第1帶隙(即第1、2能帶之間的間隙)明顯向低頻擴寬。特別是對于第2帶隙,彈性模量為復數時比視為常數時寬了將近1倍。對比只考慮儲能模量和同時考慮儲能模量和損耗模量的情況,發現:兩者的第1、3階能帶基本上重合,而第2階能帶變化較大;考慮復模量的情況下第2階能帶被推向更高的頻率范圍,從而使第1帶隙的寬度增大。這說明,材料的黏彈阻尼對聲子晶體能帶結構具有重要的影響,彈性模量越大,能帶的頻率也越高。由于儲能模量隨頻率呈現增大的趨勢,在低頻時比平均值要小,使得第1階能帶的頻率比彈性模量為常數時低,而在高頻時儲能模量比其平均值要大,從而使得第2、3階能帶比彈性模量為常數時的高。對于損耗模量,由于它只在阻尼峰附近存在較大的值,因此只對這一頻率范圍內的能帶產生較大的影響。

為了深入分析損耗模量對聲子晶體能帶結構的影響,在黏彈性材料的松弛時間分別為10-1、10-2、10-3、10-4和10-5s時,計算并對比了考慮損耗模量和不考慮損耗模量時聲子晶體的能帶結構,對比結果如圖5所示。

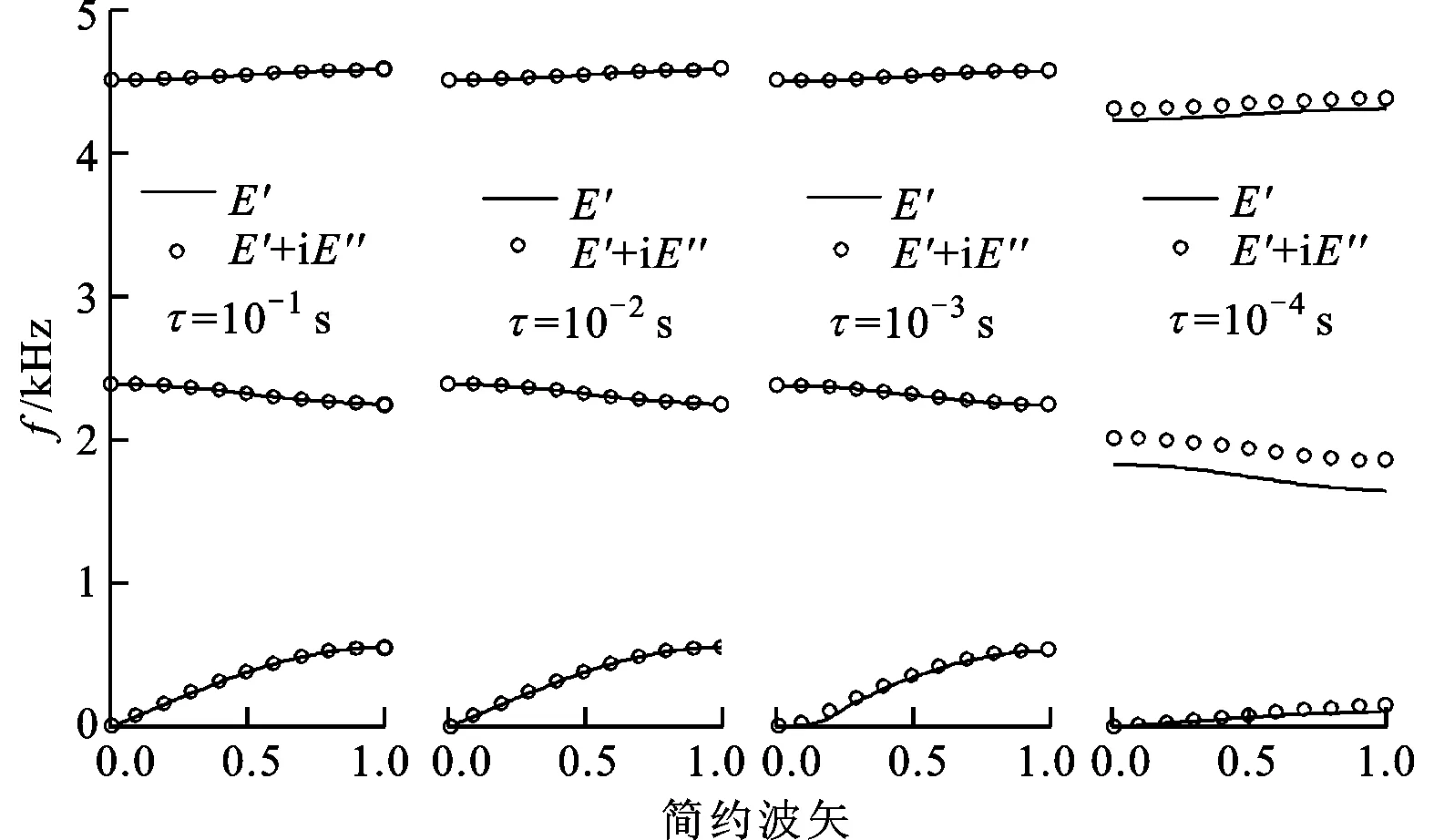
(a)τ=10-1 s, 10-2 s, 10-3 s, 10-4 s

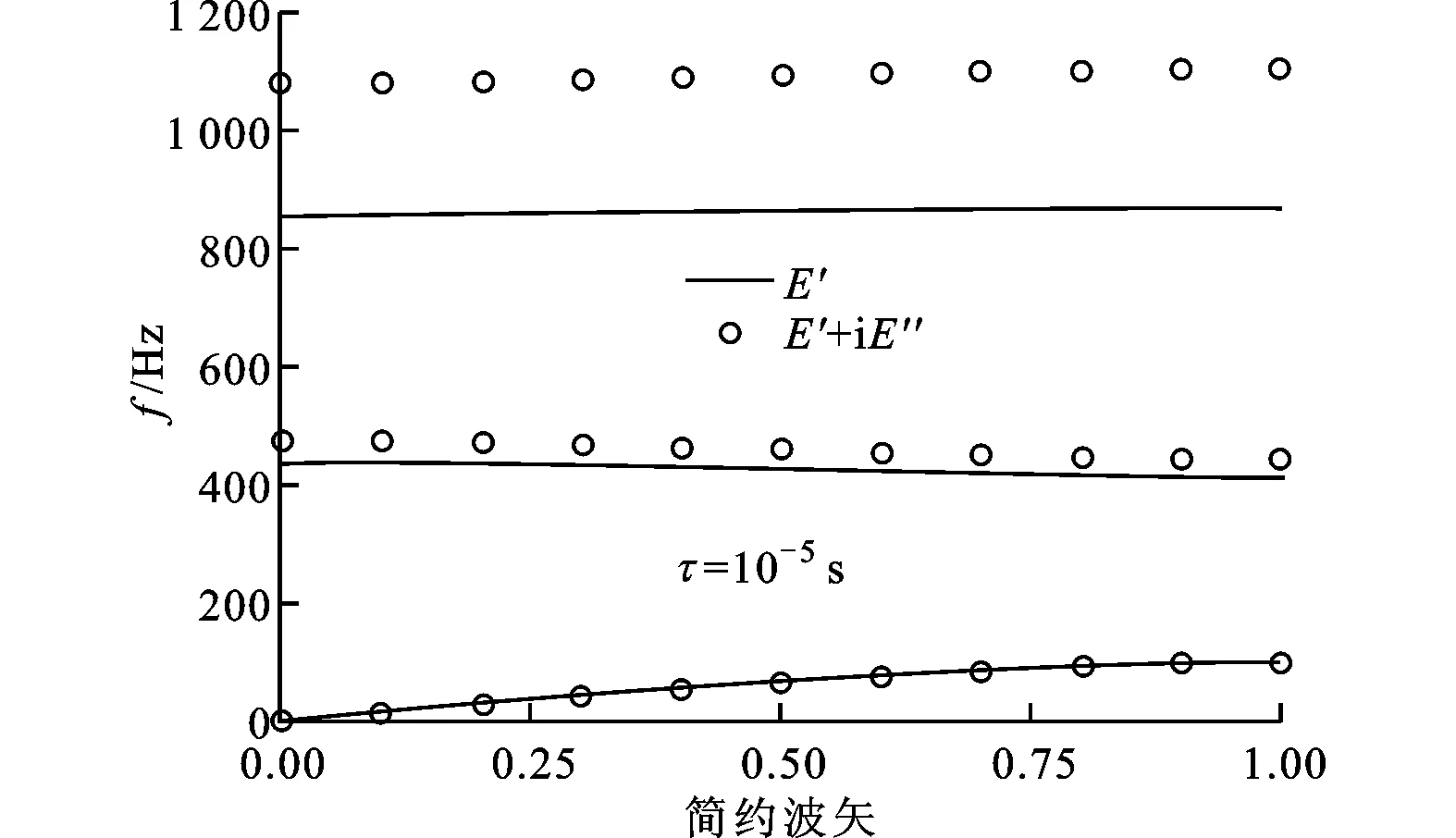
(b)τ=10-5 s

當τ不小于10-2s時,從圖3可知,黏彈性材料的阻尼峰位于20 Hz以下,在20 Hz～5kHz范圍內損耗模量減小為0,而儲能模量幾乎保持為常數。因此,在圖5a中,τ=10-1s和τ=10-2s時是否考慮損耗模量對能帶結構及其帶隙特性并無影響。當松弛時間τ減小為10-3s時,阻尼峰位于167 Hz左右,儲能模量也在這一頻率附近劇增,從而使位于這一頻率附近的能帶發生彎曲,而且考慮損耗模量與不考慮損耗模量所得的能帶有一定的偏移。當τ=10-4s時,阻尼峰位于1 667 Hz左右,因此損耗模量對位于1 750 Hz左右的第2階能帶存在較大的影響,而對于其他階次的能帶影響較小。值得注意的是,此時位于阻尼峰下方的第1階能帶的頻率相比于前3種情況降低了很多,這是由于所處頻率范圍的儲能模量接近最小值的緣故。當τ=10-5s時,阻尼峰位于10 kHz以上。從圖3可以看到,儲能模量和損耗模量在5kHz以下范圍內的值都很小,儲能模量位于最小值附近,而損耗模量接近于0,這使得聲子晶體的各階能帶頻率都有很大降低(如圖5b所示)。由于儲能模量和損耗模量在1 200 Hz以下范圍都隨頻率緩慢增大,而且損耗模量的增速更快,因此,損耗模量的影響隨著能帶階次的升高變大,帶隙的寬度也增大得更多。

為了進一步明確材料黏彈性對位于其阻尼峰附近能帶的調節作用和機理,對圖5a中τ=10-3s時連續跨過了黏彈性材料阻尼峰的第1能帶進行了研究,并計算了相應的相速度vp和群速度vg的色散關系,結果如圖6所示。彈性縱波在彈性細長桿中傳播時,其速度(即相速度)由材料的密度和彈性模量決定,即vp=(E*/ρ)1/2。同時,相速度決定了能帶的斜率,即vp=ω/k。群速度表示彈性波能量的傳播速度,其值等于能帶上某點的切線斜率。圖6中分別對比了彈性模量為實常數(EC)、只考慮儲能模量(E′)和同時考慮儲能模量及損耗模量(E′+iE″)時的色散關系。

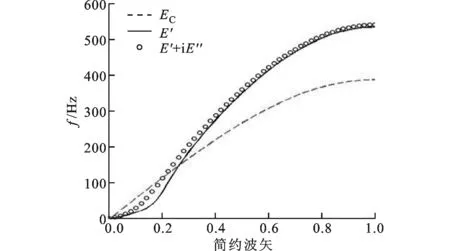
(a)能帶結構

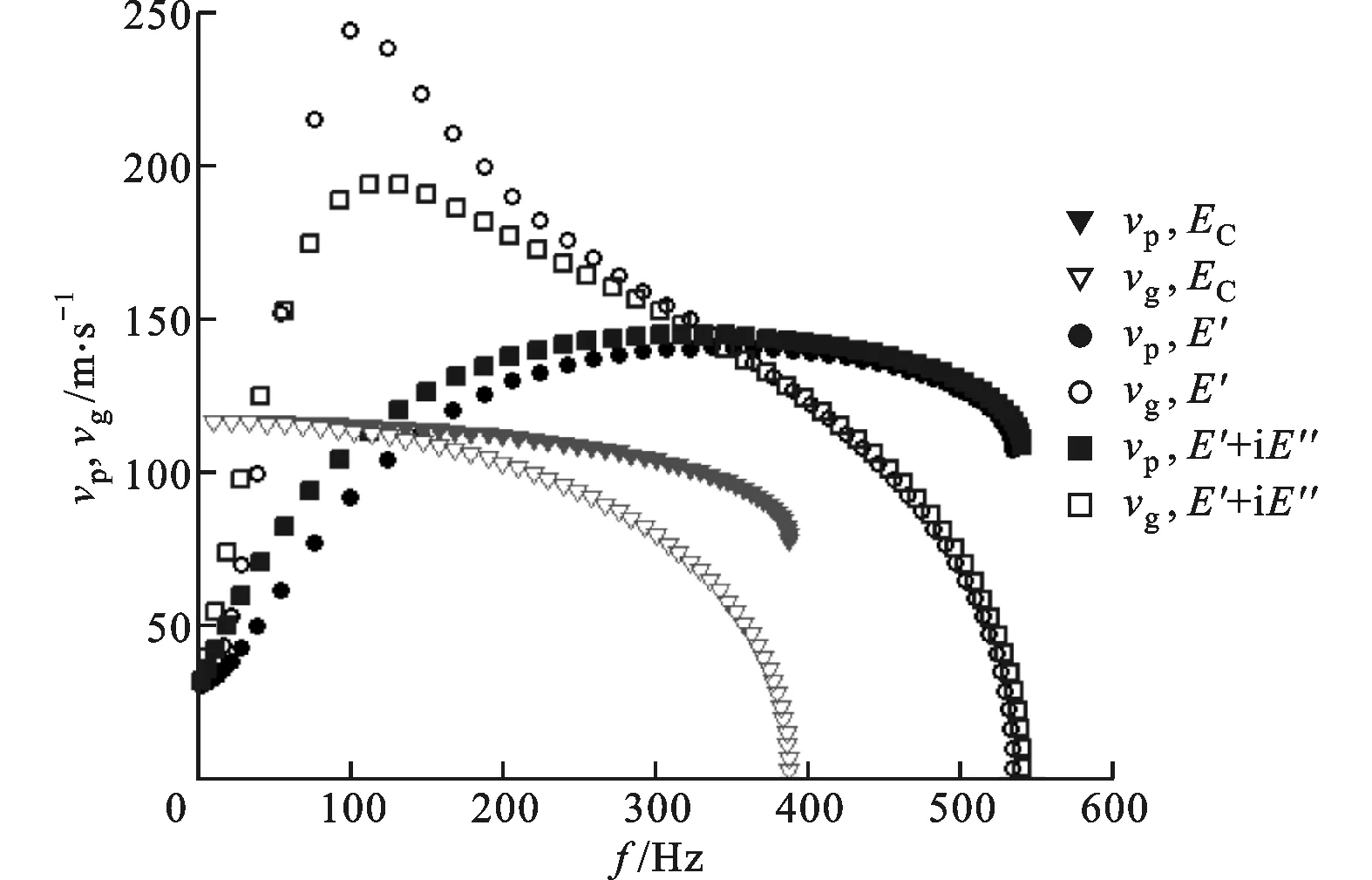
(b)相速度及群速度色散關系

對于彈性模量為實常數的情況,在低頻范圍由于波長較大,彈性波在周期結構中傳播與在均勻介質中無異,色散關系近似呈線性,如圖6a中虛線所示,相應的相速度和群速度也基本保持不變,如圖6b中的實心和空心三角曲線所示。由于黏彈性的引入,儲能模量和損耗模量都在阻尼峰附近發生急劇的變化,使得結構的色散關系呈非線性。由于聲子晶體的2種組元的密度和彈性模量相差很大,彈性波在其中傳播時,金屬層的位移遠小于黏彈性橡膠的位移。聲子晶體可以等效為由如圖1a所示模型連接質量塊組成的一維彈簧-質量-阻尼系統。在極低頻,聲子晶體相當于由彈簧(E2)連接質量塊組成的完全彈性系統,其色散關系也呈線性,只不過此時相速度和群速度很小,如圖6a、6b中20 Hz以下部分所示。當頻率接近阻尼峰頻率(167 Hz)時,一方面,儲能模量的增大使得彈性波在結構中的傳播速度和能量的傳播速度也增大,如圖6b中20～300 Hz范圍實心、中空圓組成的色散關系曲線所示,能帶也隨之向高頻偏移,如圖6a中20～300 Hz范圍的實線所示。另一方面,損耗模量的增大也使得系統的等效彈性模量增大,導致彈性波在結構中的傳播速度增大,能帶繼續向高頻偏移,但同時由于黏性元件的黏滯力作用,一部分能量不斷地耗散在結構中不能向前傳播,能量的傳播速度略有降低,如圖6b中圓形和方形符號表示的群速度色散關系曲線所示。色散關系曲線在阻尼峰附近的頻率范圍內變化最大。當頻率高于阻尼峰時,系統又近似為完全彈性系統,彈性波在結構中的傳播速度趨于最大值,而且損耗模量對色散關系的影響逐漸消失,如圖6中300～350 Hz范圍內的曲線所示。對于350 Hz以上部分,由于內部周期結構對波的多重散射作用,加上前向波與返回波的相互作用,形成了如圖6b所示的色散關系,并在布里淵區邊界形成彈性波帶隙。能帶向低頻彎曲,相速度略有降低,而群速度在帶隙邊界上減小為0,表明此時能量無法向前傳播,即表示帶隙產生。

4 結 論

本文根據黏彈性材料的標準線性固體模型,利用平面波展開法的迭代算法對由黏彈性材料組成的一維聲子晶體的能帶結構及帶隙特性進行了計算和理論分析。由于材料黏性的頻率相關性,儲能模量和損耗模量都是頻率的函數,從而對聲子晶體的能帶結構產生了重大影響。對比結果表明,損耗模量對能帶結構的影響與頻率有關,在阻尼峰值附近的頻率范圍內,損耗模量的影響最大,是不容忽視的,位于此頻率范圍的能帶被調向更高頻。在其他頻率范圍,損耗模量的影響較小,能帶位置基本保持不變,此時才可以只考慮儲能模量的影響[15-19]。調節阻尼峰的頻率值使其接近聲子晶體的某一能帶,就能夠通過損耗模量來調節任一能帶,從而使此能帶下方的帶隙變寬,上方的帶隙變窄。材料黏彈性對聲子晶體能帶結構的這些影響歸因于材料黏彈阻尼的頻率相關性。本文的研究結果可以為黏彈性阻尼材料應用于聲子晶體提供一定的理論基礎,也為調節聲子晶體能帶結構和獲得寬頻帶隙提供了一種新的方法。

[1] 溫熙森, 溫激鴻, 郁殿龍, 等.聲子晶體 [M].北京: 國防工業出版社, 2009: 2.

[2] SIGALAS M, ECONOMOU E N.Elastic and acoustic wave band structure [J].Journal of Sound and Vibration, 1992, 158(2): 377-382.

[3] SIGALAS M, ECONOMOU E N.Band structure of elastic waves in two-dimensional systems [J].Solid State Commun, 1993, 86(3): 141-143.

[4] KUSHWAHA M S, HALEVI P, DOBRZYNSKI L, et al.Acoustic band structure of periodic elastic composites [J].Physical Review Letters, 1993, 71(13): 2022-2025.

[5] MARTINEZ-SALA R, SANCHO J, SANCHEZ J V, et al.Sound attenuation by sculpture [J].Nature, 1995, 378: 241.

[6] ZHU Xuefeng, LIU Shengchun, XU Tao, et al.Investigation of a silicon-based one-dimensional phononic crystal plate via the super-cell plane wave expansion method [J].Chinese Physics: B, 2010, 19(4): 044301.

[7] TANAKA Y, TOMOYASU Y, TAMURA S.Band structure of acoustic waves in phononic lattices: two-dimensional composites with large acoustic mismatch [J].Physical Review: B, 2000, 62(11): 7387-7392.

[8] LIU Zhengyou, CHAN C T, SHENG Ping, et al.Elastic wave scattering by periodic structures of spherical objects: theory and experiment [J].Physical Review: B, 2000, 62(4): 2446-2457.

[9] SPRIK R, WEGDAM G H.Acoustic band gaps in composites of solids and viscous liquids [J].Solid State Commun, 1998, 106(2): 77-81.

[10]ZHANG Xin, LIU Zhengyou, MEI Jun, et al.Acoustic band gaps for a two-dimensional periodic array of solid cylinders in viscous liquid [J].Journal of Physics: Condensed Matter, 2003, 15: 8207-8212.

[11]周光泉, 劉孝敏.黏彈性理論 [M].合肥: 中國科學技術大學出版社, 1996: 5.

[12]PSAROBAS I E.Viscoelastic response of sonic band-gap materials [J].Physical Review: B, 2001, 64(1): 012303.

[13]HUSSEIN M I.Theory of damped Bloch waves in elastic media [J].Physical Review: B, 2009, 80(21): 212301.

[14]HUSSEIN M I, FRAZIER M J.Band structure of phononic crystals with general damping [J].Journal of Applied Physics, 2010, 108(9): 093506.

[15]王剛, 溫激鴻, 劉耀宗, 等.一維黏彈材料周期結構的振動帶隙研究 [J].機械工程學報, 2004, 40(7): 47-50.WANG Gang, WEN Jihong, LIU Yaozong, et al.Research on the vibration band gaps of one dimensional viscoelastic periodic structure [J].Chinese Journal of Mechanical Engineering, 2004, 40(4): 47-50.

[16]溫激鴻, 王剛, 劉耀宗, 等.金屬/丁腈橡膠桿狀結構聲子晶體振動帶隙研究 [J].振動工程學報, 2005, 18(1): 1-7.

WEN Jihong, WANG Gang, LIU Yaozong, et al.Research on vibration band gaps of one dimensional phononic crystals consisted of metal and nitrile butadiene rubber [J].Journal of Vibration Engineering, 2005, 18(1): 1-7.

[17]胡家光, 張晉, 張茜, 等.一維花崗巖/丁腈橡膠聲子晶體的帶隙及其應用 [J].云南大學學報: 自然科學版, 2006, 28(6): 504-508.HU Jiaguang, ZHANG Jin, ZHANG Xi, et al.Band gaps and application of one-dimensional phononic crystals consisted of granite and nitrile rubber [J].Journal of Yunnan University: Natural Science, 2006, 28(6): 504-508.

[18]ZHAO Y P, WEI P J.The band gap of 1D viscoelastic phononic crystal [J].Computational Materials Science, 2009, 46(3): 603-606.

[19]WEI P J, ZHAO Y P.The influence of viscosity on band gaps of 2D phononic crystal [J].Mechanics of Advanced Materials and Structures, 2010, 17(6): 383-392.

[20]MERHEB B, DEYMIER P A, JAIN M, et al.Elastic and viscoelastic effects in rubber/air acoustic band gap structures: a theoretical and experimental study [J].Journal of Applied Physics, 2008, 104(6): 064913.

[21]MERHEB B, DEYMIER P A, MURALIDHARAN K, et al.Viscoelastic effect on acoustic band gaps in polymer-fluid composites [J].Modelling and Simulation in Materials Science and Engineering, 2009, 17(7): 075013.

[22]LIU Yaozong, YU Dianlong, ZHAO Honggang, et al.Theoretical study of two-dimensional phononic crystals with viscoelasticity based on fractional derivative models [J].Journal of Physics: D Applied Physics, 2008, 41(6): 065503.

[23]LAHES R.Viscoelastic materials [M].New York, USA: Cambridge University Press, 2009: 63-64.

(編輯 管詠梅)

Damping-InducedFrequencyShiftsinBandStructuresofOne-DimensionalViscoelasticPhononicCrystalRods

ZHANG Siwen1,2,WU Jiuhui1,2,LIU Zhangyi1,2

(1.School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 71009, China; 2.State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China)

To understand the influence of damping on the band structures of phononic crystals (PCs), the vibration band structures of one-dimensional viscoelastic PCs are investigated and analyzed theoretically by iteration method for plane wave expansion (PWE), based on standard linear solid (SLS) model of viscoelastic materials.Compared with the case of constant modulus, the storage modulus and the loss modulus exert clearer influence on the band structures and the gap bandwidth due to the frequency dependence of the complex modulus.In particular, the influence of loss modulus cannot be ignored in the frequency range around the damping peak, where the frequency bands are shifted to the higher range, but the other bands almost remain unchanged, thus the gaps below and above the bands are widened and narrowed respectively.These results provide theoretical basis to research viscoelastic phononic crystals and an effective way to obtain broad band gaps for phononic crystals.

phononic crystal; band structure; viscoelastic material; damping; band gap

10.7652/xjtuxb201403005

2013-08-08。

張思文(1985—),男,博士生;吳九匯(通信作者),男,教授,博士生導師。

國家自然科學基金資助項目(51075325);教育部新世紀優秀人才支持計劃資助項目(NCET-09-0644)。

TB535; O328; O345

:A

:0253-987X(2014)03-0022-06