卷積法和角譜法再現顯微全息圖時補零數的研究

李建素,王昭,高建民,劉蕓

(1.西安交通大學機械工程學院, 710049, 西安;2.西安交通大學機械制造系統工程國家重點實驗室, 710049, 西安)

卷積法和角譜法再現顯微全息圖時補零數的研究

李建素1,王昭1,高建民2,劉蕓1

(1.西安交通大學機械工程學院, 710049, 西安;2.西安交通大學機械制造系統工程國家重點實驗室, 710049, 西安)

針對全息圖補零法的補零數對再現像和系統效率的影響,結合數字全息顯微術中卷積法和角譜法數字再現的原理和再現面與物體放大像尺寸的關系,研究補零數對再現像和系統效率的影響,并采用梯度法來評價再現像的質量。對全息圖采用頻率濾波提取實像或共軛像的頻譜,再采用卷積法或角譜法數字再現,獲得物體的放大像。結合再現像的質量和效率兩方面因素,提出了補零數的選取依據，即以再現面的物理尺寸不小于物體的放大像時的最小補零數作為最佳補零數,此時能以最小的計算量獲得最高質量的再現像。通過實驗驗證,結果與理論分析一致,證明了選取補零數的依據。

顯微全息圖;補零數;卷積法;角譜法

數字全息顯微術因能夠同時記錄和再現物體的三維信息,并以無入侵性和非接觸的方式對樣本進行測量,在微觀粒子成像和跟蹤[1-2]、聚合物生長檢測[3-4]、生物細胞觀察[5-8]等領域得到了廣泛的應用。在數字全息中,最常用的數字再現方法有菲涅耳衍射法,卷積法和角譜法。其中菲涅耳衍射法是對基爾霍夫衍射理論的一種近似算法,此算法要求再現距離滿足菲涅耳近似條件;卷積法和角譜法分別以卷積和角譜的形式無近似地表示瑞利-索末菲衍射理論,實現數字再現。菲涅耳法適用于再現距離大于額定距離的數字再現,卷積法和角譜法適用于再現距離小于額定距離的數字再現[9],且能夠無近似地再現物光波。因此,卷積法、角譜法比菲涅耳法能夠更準確地再現全息圖。但是卷積法再現顯微全息圖時獲得的再現像常常折疊,如北京工業大學的趙潔等人采用卷積法再現時,當再現距離大于最佳再現距離時,再現像被放大、發生折疊、視場不完整[10]。日本群馬大學的Zhang等人采用卷積法再現時,再現像出現折疊,未能獲得正確的再現像[11]。法國勒芒大學的Picart等人采用卷積法再現時,再現像出現折疊,零級像干擾再現實像[12]。上述折疊現象發生是由于卷積法再現時再現面的物理尺寸小于再現像的物理尺寸,從而導致了再現像面的折疊。角譜法和卷積法唯一區別是它們的傳遞函數在不同的域表示——卷積法的傳遞函數在空域表示,角譜法的傳遞函數在頻域表示。角譜法與卷積法的計算理論是一樣的,因此在角譜法再現顯微全息圖時也常常會出現再現像的折疊。

為了避免卷積法和角譜法再現顯微全息圖時導致再現像的折疊,趙潔,Zhang和Picart等人提出了在全息圖周圍填充灰度值為零的像素,進而增大再現面的物理尺寸的方法,即全息圖補零法,以獲得無折疊的再現像[10-12]。但是，他們并未就補零數對再現像和系統效率的影響進行系統的分析,也未給出補零數的選取依據。本文在卷積法和角譜法基本原理的基礎上,結合放大像尺寸與再現面尺寸的關系,分析了補零數對再現像和系統效率的影響,給出了最佳補零數選取的理論和實驗依據。

1 數字再現原理

數字全息顯微術中的坐標關系如圖1所示。

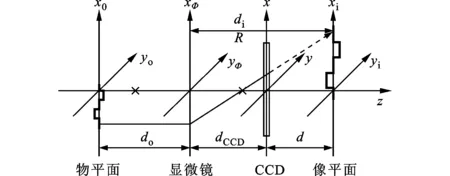
圖1 數字全息顯微術坐標示意圖

根據瑞利-索末菲衍射理論和線性系統理論,數字再現的物光波為

O(xi,yi)=?C(x,y)I(x,y)h(xi-x,yi-y)dxdy

(1)

式中:I(x,y)和C(x,y)分別為全息圖和再現光的表達式;h(x,y)為光波衍射的脈沖響應,可表示為

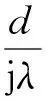
(2)

其中d為記錄距離,λ為激光波長。

對式(2)做傅里葉變換,可得

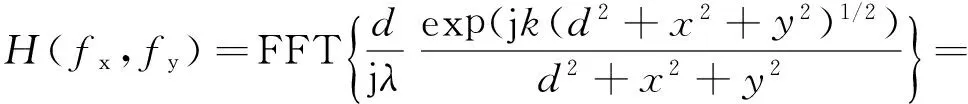
(3)

式中:H(fx,fy)是光波衍射的傳遞函數;FFT{A}為A的傅里葉變換。根據卷積定理,式(1)可以改寫為

FFT{O(xi,yi)}=

FFT{C(x,y)I(x,y)}H(fx,fy)

(4)

對式(4)兩邊同時做逆傅里葉變換,并結合式(1)可得再現物光波為

O(xi,yi)=IFFT{FFT{C(x,y)I(x,y)}·

FFT(h(x,y))}

(5)

或

O(xi,yi)=IFFT{FFT{C(x,y)I(x,y)}·

H(fx,fy)}

(6)

式中:IFFT{A}為A的逆傅里葉變換。式(5)為卷積法數字再現的表達式,式(6)為角譜法數字再現的表達式。式(5)和式(6)僅傳遞函數的表示形式不同,但都是首先對全息圖進行一次傅里葉變換后與傳遞函數相乘,再做逆傅里葉變換獲得再現物光波。全息圖經歷了2次傅里葉變換之后得到再現物光波,故再現面與全息圖同屬于空域,表明卷積法和角譜法再現的再現面的像素大小與全息圖的像素大小相等,因而它們的再現面尺寸為

Si=MΔxi×NΔyi

(7)

式中:M、N為全息圖的像素數;Δxi、Δyi為再現面的像素大小。

本文首先對全息圖采用頻率濾波提取實像或共軛像的頻譜,再采用卷積法或角譜法數字再現,獲得物體的放大像,流程如圖2所示。

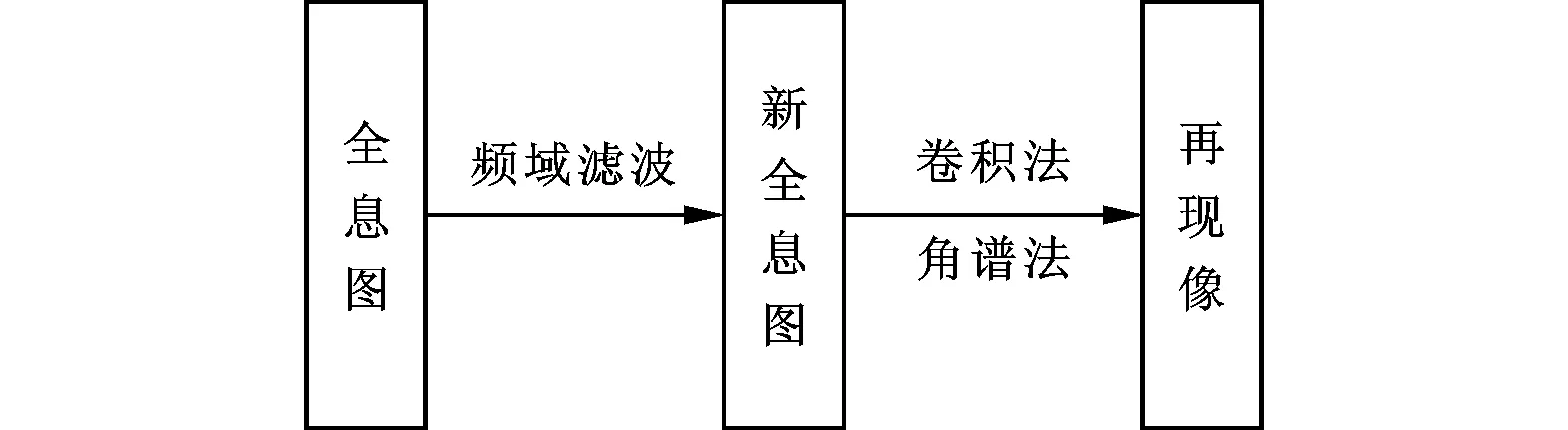
圖2 數字全息再現流程圖

數字再現獲得的物體放大像的尺寸為

Sβo=βX×βY

(8)

式中:β為系統的放大倍數;X、Y分別為物體的長和寬。數字全息顯微術再現獲得物體放大的像,再現面的尺寸可能小于放大像,即Sβo>Si。此時為避免采用快速傅里葉變換實現卷積法或角譜法而導致的再現像折疊,有學者提出對全息圖補零以增大再現面的尺寸,從而獲得無折疊的再現像。當再現面的物理尺寸小于物體的放大像,即M<βX/Δxi,N<βY/Δyi時,需對全息圖補零至M′≥βX/Δxi,N′≥βY/Δyi,以獲得不折疊的再現像。本文的補零方式是在全息圖的x、y方向分別對稱地補相同數量的零,后續提到的補零數都是指在某一方向上某一邊的補零數。因此,對全息圖補零的最小補零數為

(9)

因卷積法和角譜法再現時,再現面的像素大小與CCD(Charged-Coupled Device)面的像素大小相等,即Δxi=Δx,Δyi=Δy,則式(9)可改寫為

(10)

式(10)決定的補零數即為最佳補零數,此時能夠以最高的效率獲得高質量的再現像。當補零數大于式(10)的補零數時,再現像質量保持恒定,但計算量隨著補零數的增加而增大,導致效率降低。

2 實驗結果和分析

為了驗證理論分析,進行了相應的實驗。實驗光路如圖3所示,圖中He-Ne激光器發出的光經過W1(1/2波片)和偏振分光棱鏡(PBS)分為兩束,一束經空間濾波器(BE1)擴束和透鏡L1準直后作為參考光(R);另一束經W2(1/2波片)后直接照射物體并被顯微物鏡(MO)放大后作為物光(O),物光與參考光波經分光棱鏡合束后干涉形成全息圖。圖中M1、M2均為反射鏡。顯微物鏡的放大倍數為10,數值孔徑為0.25。物體為USAF1951分辨率板的6組和7組黑白條紋,其尺寸X×Y為0.2 mm×0.2 mm。分辨率板的最小線寬為2.19 μm。

實驗獲得了多組數據,且數據具有較好的一致性。本文列舉了一組實驗數據,采集的全息圖如圖4a所示,其像素數為842×842,像素大小為9 μm×9 μm,記錄距離d為214.02 mm。系統放大倍數β經分辨率板標定為51.4。因為卷積法和角譜法對全息圖的處理相同,僅是計算時的傳遞函數表達形式不同,故這兩種方法的數字再現結果近似，所以本文僅討論卷積法數字再現的情況。按照圖2所示的流程對全息圖進行處理,采用卷積法數字再現全息圖得到再現像,如圖4b所示。

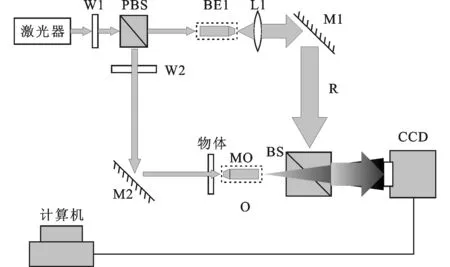
W1:1/2波片;W2:1/2波片;MO:顯微物鏡;BE1:空間濾波器;L1:透鏡;M1,M2:反射鏡;PBS:偏振分光棱鏡;BS:分光棱鏡

(a)全息圖

(b)卷積法再現的再現像

因βX=51.4×0.2 mm=10.28 mm,MΔx=7.578 mm,10.28>7.578,導致了再現像折疊,因此需對全息圖補零后再進行數字再現。由于待測物體的長寬相等,為簡化計算,僅分析x方向再現像。據式(9),全息圖補零后最小像素數M′=βX/Δx=1 142。全息圖最小補零數為

Mpaddingmin=(βX/Δx-M)/2=150

(11)

(a)Mpadding=100,Npadding=100

(b)Mpadding=150,Npadding=150

(c)Mpadding=450,Npadding=450

設全息圖的縱向補零數Mpadding的范圍為50～450,橫向補零數Npadding的范圍為50～450,補零數每增加50像素數,再現一次再現像。為了簡潔,本文不列出每個補零數對應獲取的再現像,僅列出具有代表性的3幅再現像(見圖5)。由圖5可知:當補零數小于150時,再現像折疊,且再現像的對比度很低;當補零數等于150時,再現像清晰,再現像對比度很高,且能分辨分辨率板的7.6組條紋,分辨率大于2.19 μm;當補零數大于150時,再現像仍能分辨分辨率板的最高級條紋,分辨率大于2.19 μm。從理論上分析,隨著補零數的增加,僅是增加了再現面的尺寸,當保證再現面能夠容納放大像之后,再現像都能夠清晰再現。實驗結果與理論分析一致,當補零數等于150時,再現像不折疊,與第2節給出的最小補零數吻合。將再現像折疊時的再現像質統一視為0,采用圖像的梯度法評價不重疊的再現像。設再現像的灰度為f(x,y),則再現像的梯度表示為

(12)

式中:Gx、Gy分別為再現像的橫向梯度和縱向梯度。本文采用Sobel梯度算子理論。由式(12)獲得的圖像梯度值越大，說明圖像的邊緣越陡峭,圖像的對比度越大,圖像的質量越好。評價結果如圖6所示。

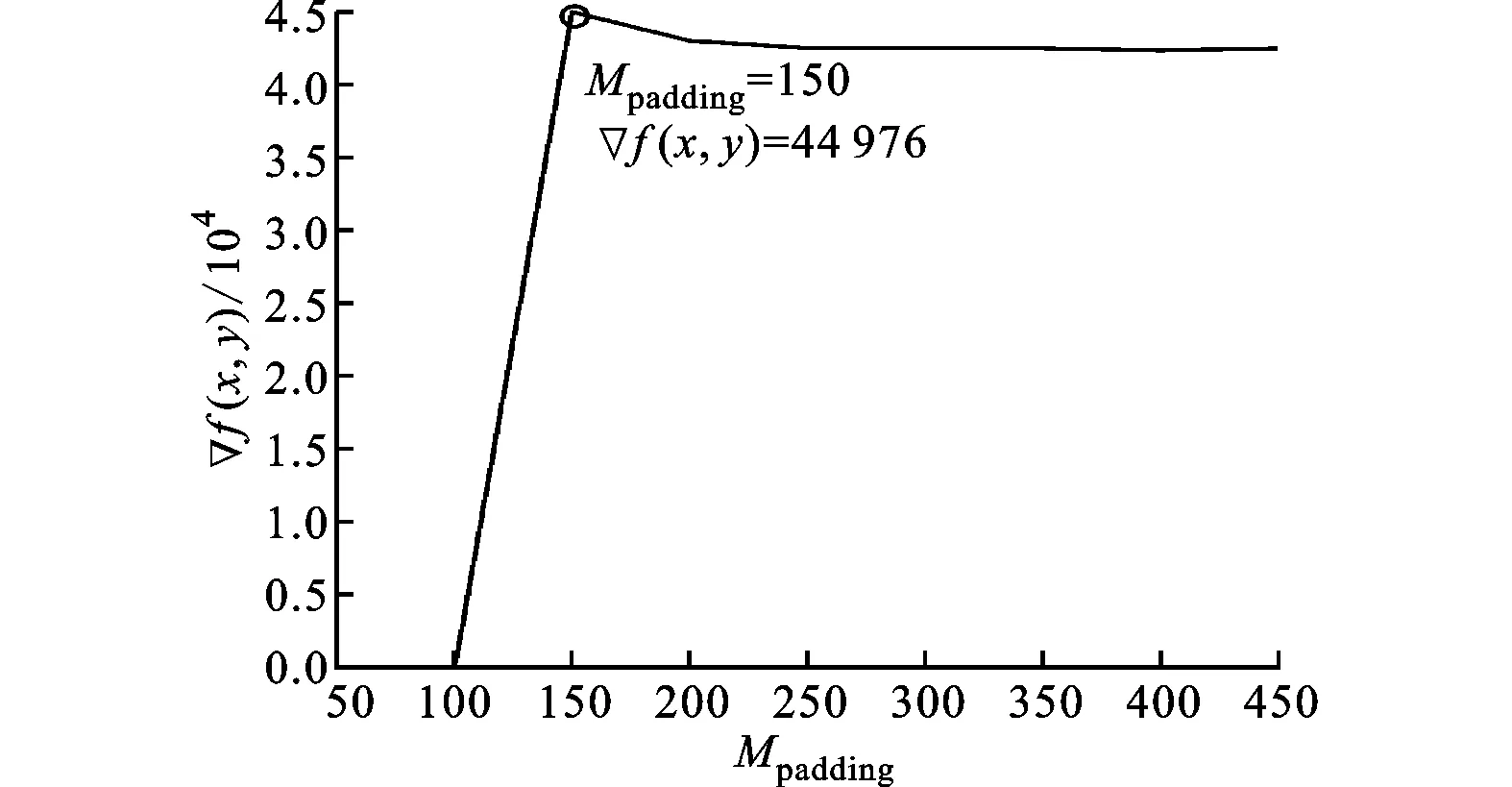
圖6 再現像質量圖

由圖6得,當補零數為150時,再現像的質量最好。補零數為150正是計算得到的最小補零數,表明當補零數為最小補零數時,再現像質量最好。當補零數大于150時,隨著補零數的增加,再現像的質量略有降低,并最后保持恒定。這是因為補零數大于最小補零數后,繼續增加補零數時,再現實像周圍的噪聲進入再現面,導致再現像的質量稍有降低,但頻率濾波獲取的頻譜里含有的噪聲是固定的,噪聲不會隨著補零數的增加繼續增大。

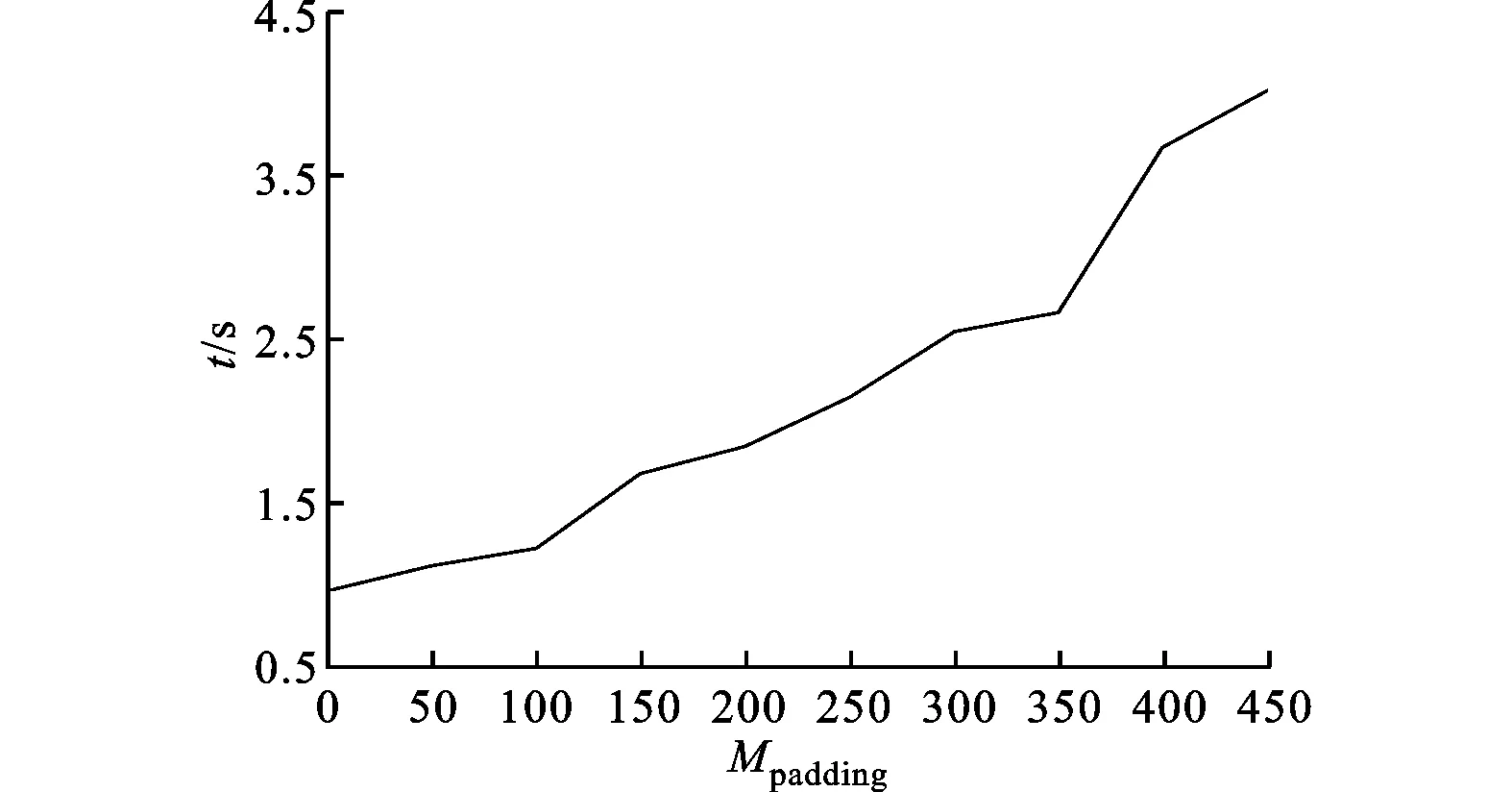
圖7 補零數與計算耗時的關系

為了評估不同補零數的計算耗時,給出了補零數與耗時的關系,如圖7所示。由圖7可得,隨著補零數的增大,計算時間增加,整個系統的效率越來越低。考慮再現像的質量和效率兩方面,應選擇補零數為150,此時既能獲得高質量的再現像,又能以最短的時間完成計算。

實驗表明,應選擇恰好能使再現面尺寸等于放大像尺寸時的補零數作為最佳補零數,此時能以最高的效率獲得最高質量的再現像。實驗結果與理論分析一致。

3 結 論

本文結合數字全息顯微術中卷積法和角譜法數字再現的原理和再現面與物體放大像尺寸的關系,系統地就補零數對再現像和系統效率的影響進行了分析研究,并提出了補零數的選取依據。通過理論分析和實驗,論證了選擇使再現面尺寸等于物體放大像尺寸時的最小補零數作為最佳的全息圖補零數,能以最高效率獲得最高質量的再現像。

[1] GE Baozhen, LV Qieni, ZHANG Yimo. Particle digital in-line holography with spherical wave recording [J]. Chinese Optics Letters, 2003, 1(9): 517-519.

[2] 呂且妮, 葛寶臻, 高巖, 等. 乙醇噴霧場粒子尺寸和速度的數字全息測量 [J]. 光子學報, 2010, 39(2): 266-270. LV Qieni, GE Baozhen, GAO Yan, et al. Simultaneous measurement of size and velocity of alcohol spray with digital holography [J]. Acta Photonica Sinica, 2010, 39(2): 266-270.

[3] CAVALLINI L, BOLOGNESI G, LEONARDO R D. Real-time digital holographic microscopy of multiple and arbitrarily oriented planes [J]. Optics Letters, 2011, 36(17): 3491-3493.

[4] MEROLA F, MICCIO L, PATURZO M, et al. Driving and analysis of micro-objects by digital holographic microscope in microfluidics [J]. Optics Letters, 2011, 36(16): 3079-3081.

[5] SHIN D, DANESHPANAH M, ANAND A, et al. Optofluidic system for three-dimensional sensing and identification of micro-organisms with digital holographic microscopy [J]. Optics Letters, 2010, 35(23): 4066-4068.

[6] KEMPER B, BALLY G V. Digital holographic microscopy for live cell applications and technical inspection [J]. Applied Optics, 2007, 47(4): 52-61.

[7] RAPPAZ B, MARQUET P, CUCHE E, et al. Measurement of the integral refractive index and dynamic cell morphometry of living cells with digital holographic microscopy [J]. Optics Express, 2005, 13(23): 9361-9373.

[8] JAVIDI B, MOON I, YEOM S, et al. Three-dimensional imaging and recognition of microorganism using single-exposure on-line (SEOL) digital holography [J]. Optics Express, 2005, 13(12): 4492-4506.

[9] SYPEK M, PROKOPOWICZ C, GRECKI M. Image multiplying and high-frequency oscillations effects in the Fresnel region light propagation simulation [J]. Optical Engineering, 2003, 42(11): 3158-3164.

[10]趙潔. 微結構相襯成像的數字全息方法研究 [D]. 北京: 北京工業大學, 2011.

[11]ZHANG F, YAMAGUCHI I, YAROSLAVSKY L P. Algorithm for reconstruction of digital holograms with adjustable magnification [J]. Optics Letters, 2004, 29(14): 1668-1670.

[12]LI J C, TANKAM P, PENG Z J, et al. Digital holographic reconstruction of large objects using a convolution approach and adjustable magnification [J]. Optics Letters, 2009, 34(5): 572-574.

[本刊相關文獻鏈接]

田福慶,羅榮,李萬,等.改進的卷積型小波包分解及在故障診斷中的應用.2014,48(3):89-95.[doi:10.7652/xjtuxb 201403017]

杜飛,洪軍,李寶童,等.結合面參數的超聲檢測方法研究.2013,47(3):18-23.[doi:10.7652/xjtuxb201303004]

曲翀,王秀麗,謝紹宇,等.含風電電力系統隨機生產模擬的改進算法.2012,46(6):115-121.[doi:10.7652/xjtuxb2012 06020]

張先玉,劉郁林,王開.超寬帶通信壓縮感知信道估計與信號檢測方法.2010,44(2):88-91.[doi:10.7652/xjtuxb201002 018]

方杰,韋穗,霍修坤.超聲衍射層析成像的高精度核卷積插值重建算法.2009,43(10):94-98.[doi:10.7652/xjtuxb200910 020]

何茂剛,郭盈,鐘秋,等.一種新的測定流體質擴散系數的全息干涉圖像處理方法.2008,42(11):1350-1355.[doi:10.7652/xjtuxb200811008]

廖與禾,張鵬,郎根峰.移相軌跡及其在全息動平衡中的應用.2008,42(7):803-806.[doi:10.7652/xjtuxb200807004]

(編輯 趙煒)

Zero-PaddingNumberofConvolutionApproachandAngularSpectrumforReconstructingMicroscopicHologram

LI Jiansu1,WANG Zhao1,GAO Jianmin2,LIU Yun1

(1. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

The influence of zero-padding number in zero-padding hologram on reconstructed image and system efficiency is analyzed by combining angular spectrum in digital holographic microscopy with the size relation between magnified image and reconstructed plane. The gradient method is used to evaluate the quality of reconstructed image. The frequency of real image or virtual image is obtained by frequency filter. The object magnified image is obtained by convolution approach or angular spectrum. The evidence of choosing zero padding number is proposed according to the quality of reconstructed image and system efficiency. The experimental results are consistent with theoretical analysis. It demonstrates that the smallest zero-padding number ensuring the size of reconstructed image larger than the magnified image is the best one, at that time the highest quality of reconstructed image is achieved with smallest calculating task.

microscopic hologram; zero-padding number; convolution approach; angular spectrum

10.7652/xjtuxb201405020

2013-09-20。 作者簡介: 李建素(1986—),女,博士生;高建民(通信作者),男,教授,博士生導師。

O438.1

:A

:0253-987X(2014)05-0113-05