三種模型級聯的比較

張宇楠，曾 實

(清華大學 工程物理系，北京 100084)

同位素在生產與科研中的應用日益廣泛，各種同位素的需求量也迅速增長，尤其是利用目前最大規模和最經濟的分離鈾同位素的離心法分離非鈾的穩定同位素，推動了多組分同位素分離級聯的研究。相對于理論已相當成熟的雙組分分離級聯(特別是鈾濃縮級聯)研究，多組分分離級聯這一領域還有很多亟待解決的問題，如在傳統的級聯形式中無法實現各級之間的交匯點處各組分豐度無混合，難以合理確定各級之間最合適的連接條件；在多組分分離中未能得到公認的價值函數定義，難以利用價值函數和分離功率的概念分析和評價級聯的分離性能；一般形式的多組分分離級聯的計算牽涉到求解非線性方程組[1]，不方便進行一般性的分析和研究。此外，在涉及生產實際時，由于對穩定同位素的需求在量、種類、豐度方面的要求均不同，需建立不同的分離級聯并采用不同的運行方式，而這成本高昂、費時長。故以真實實驗的方式研究各種多組分分離不現實。

為解決這些問題，探索高效分離多組分同位素的方法，提出了模型級聯的概念。這些模型級聯是對一般形式的多組分分離級聯提出一些特殊的限制條件后得到的，它們通常具有相對簡單的形式，易于計算，又能反映多組分分離級聯的一般規律和特性，因此可作為解析或數值分析級聯性質的合適對象。模型級聯的一典型例子即雙組分分離的理想級聯，在大規模的鈾同位素分離實踐中得到檢驗，目前仍在指導生產實際中發揮重要作用。然而，對于多組分分離，提出不同的要求可得到不同的模型級聯，如要求交匯點處來流中某兩組分的豐度比相等，則得到相對豐度匹配級聯[2](matched abundance ratio cascade，MARC)；要求各級的組分分流比相等則構造出準理想級聯[3]；而采用小分離系數、連續流量的假設則構造出Q級聯[4-5]。

模型級聯無論對于實際級聯設計還是分離理論的研究均有重要作用。就前者而言，模型級聯可為實際級聯設計提供一參考。如Kolokol′tsov等[5]提出可用優化后的Q級聯為模板，設計階梯級聯逼近Q級聯的形狀；宋天明等[6]通過優化MARC分離Si同位素，證實其結果非常接近于直接優化得到的最優解，適合指導實際級聯的設計。事實上，直接對多組分分離級聯進行優化設計，計算量很大，耗時很長，通常選擇相對易計算的模型級聯給出一結果，再以此結果為初值或目標，考慮各實際因素后，進一步簡化和優化得到所需的實際設計方案，或分析實際情況中的缺陷。此外，模型級聯是分離理論研究的重要工具。如謝全新等[7]以準理想級聯為模型，研究了存在多個供取料、有物料損失的級聯分離行為；Zeng等[8]也以Q級聯為模型進行過類似的研究。實際上，無論是理想級聯、相對豐度匹配級聯，還是準理想級聯或Q級聯，人們一直在努力探索最優的分離級聯，以及最優分離的物理本質。鑒于理想級聯在指導鈾同位素分離的成功，模型級聯無論從理論和實驗上均成為了同位素分離研究中的重要對象。

本文針對最常使用的三種模型級聯，即Q級聯、MARC級聯、準理想級聯進行分析，并對它們的背景以及關鍵參數、基本的分離特性等進行總結介紹。以往的研究均發現這幾種模型級聯之間存在很大的相似性和聯系[1，9-10]，但不夠明確。本文擬通過較全面和系統的對比分析更明確地揭示其內在的聯系，進一步認識這些級聯的本質，使對三種模型分別的研究工作能在一定程度上統一起來，避免或減少不必要的分析。

1 三種模型級聯

為在相同的條件下進行對比研究，本文以傳統的雙管道逆流級聯結構為研究對象。在級聯的兩端分別獲得精料流量P和貧料流量W，在中間某級引入供料流量F，如圖1所示。

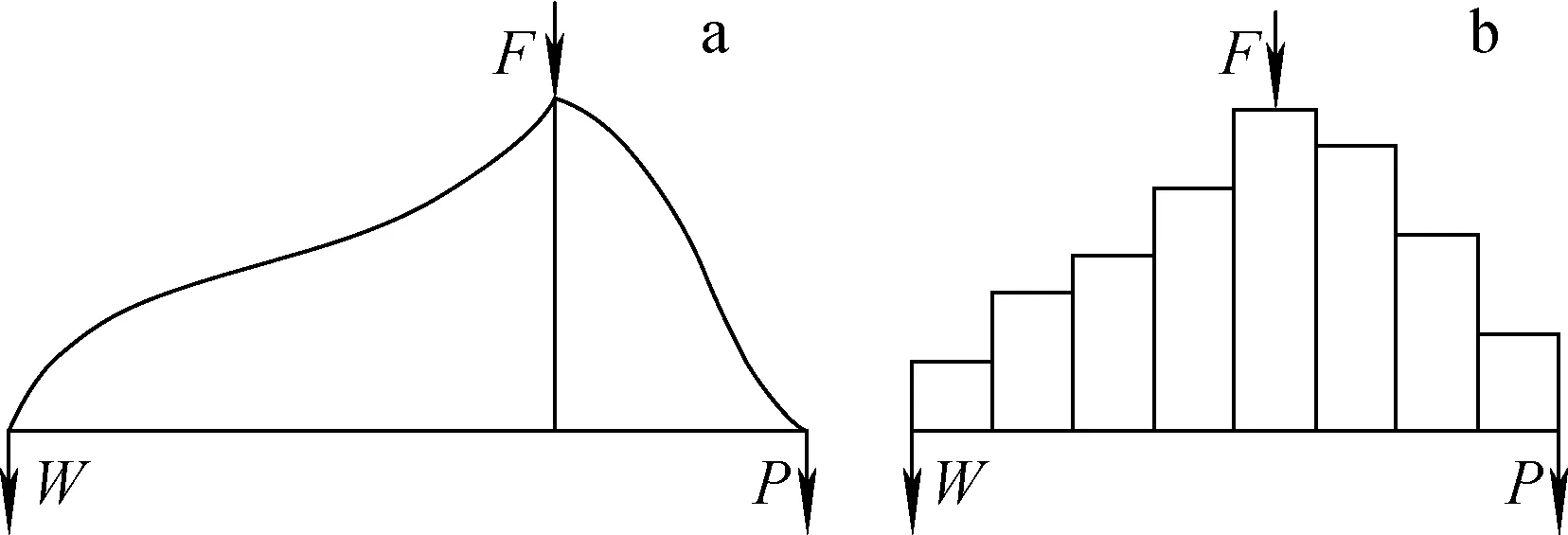
圖1 連續流量級聯結構(a)和離散流量級聯結構(b)

1.1 Q級聯

Q級聯是一種連續流量的模型級聯(model cascade of continuous profile，MCCP)，它是從MCCP的一般模型出發，通過給定一組特征函數φi(l)的特殊形式得到的[4]。Q級聯的級數為實數，流量是級數的連續函數，因此稱其為連續流量級聯。MCCP的提出是為在弱分離的情況下，通過適當簡化，將多組分分離級聯離散形式的級間物質輸運關系轉化為微分形式，設法求解微分方程得到級聯連續形式的近似解。

假如引入一組特征函數φi(l)取代各組分的豐度Ci(l)，通過一些數學手段可將微分輸運方程改寫成如下積分形式[5，11]：

貧化段

濃化段

(1)

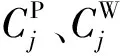
對φi(l)的要求為：

(2)

為導出Q級聯，令：

(3)

其中，流量Q滿足：

Qi-Qj=εij

(4)

在此條件下，式(1)具有特別簡單的形式，可得到：

i=1,2,…,NC

(5)

其中，SW、SP分別為Q級聯貧化段和濃縮段的長度。

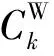
對于離心分離、擴散分離，單級的分離系數滿足如下關系：

(6)

其中：γ0為單位摩爾質量差的全分離系數；M為分子量。考慮相對濃縮系數εij：

εij=lnγij=ε0(Mj-Mi)

(7)

其中，ε0=lnγ0為單位摩爾質量差的濃縮系數，可作為衡量分離強弱的標準。

Q通常是人為給定的，因此，設：

Qi=ε0(M*-Mi)

(8)

其中，M*為虛擬組分分子量，數值給定。根據式(4)，有：

Qi∝ε0

(9)

由式(5)可知，決定Q級聯取料豐度的是QiSW和QiSP，若隨著ε0的變化，Q級聯的長度SW和SP也相應變化而使ε0SW和ε0SP不變，則級聯的各組分取料豐度就不會變化。對于Q級聯的流量分布也有類似的結論。

因此，ε0SW、ε0SP相等的Q級聯均可視為相似的，具有相似的豐度和流量分布，這也說明Q級聯模型不限于ε0遠小于1的弱分離情況。

由于Q級聯計算簡單，易于分析，為多組分分離級聯研究中最廣泛使用的模型之一，文獻[12-13]以Q級聯為模型討論了多組分分離級聯內中間質量組分的豐度分布規律與分離策略；文獻[11，14]則討論了Q級聯的優化設計問題。

1.2 MARC級聯

尋找實用的多組分同位素混合物的價值函數和分離功率的形式一直是研究的重點，眾多學者也提出了多種不同的價值函數定義形式，但均存在各自的問題而無法得到普遍的認可。文獻[2]試圖通過考察三種組分分離的特殊情況，結合對價值函數一些實用性的要求得到適用于多組分混合物的價值函數定義：設想對于不同豐度組成的多組分混合物，定義一匹配函數，當混合物的匹配函數值相等時，兩種混合物可任意混合而不產生總價值的變化。從這樣的思想出發，并借助一些數學上的推演，de la Garza等[2]得到了匹配函數與價值函數的關系，并給出了它們必須滿足的限制條件，當選取關鍵組分的相對豐度R作匹配函數值時，得到了三組分情況下各級之間不因混合而產生價值損失的級聯形式。由于是以相對豐度作為匹配標準，因此稱為相對豐度匹配級聯，即MARC。后來又將MARC的概念和相應的價值函數與分離功率定義推廣到更多組分的情況下[15]。

要確定一MARC的形式，必須事先定義兩種組分：關鍵組分，記為組分k；參考組分，記為組分n。在MARC的各級之間，要求匹配這兩種組分的相對豐度，即：

(10)

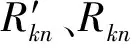
由于每個分離級的分離特性要求：

(11)

其中，αkn為兩種組分的濃化系數。結合式(10)，可知：

(12)

即MARC中的關鍵組分相對于參考組分是對稱分離的。根據式(10)、(12)以及各級質量守恒：

(13)

可得式(14)[15]：

(14)

1.3 準理想級聯

準理想級聯是文獻[3]提出的，指各分離級的組分分流比φi為常數的離散級聯。

組分分流比的定義為：

(15)

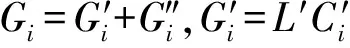
(16)

顯然，βi=φi/(1-φi)，準理想級聯的組分分流因子也保持為常數。

引入組分分流因子的概念可使多組分分離級聯的計算在形式上相對容易[17]，準理想級聯的物質輸運關系可簡化為：

(17)

(18)

(19)

其中，δsNf為Kronecker符號。

當然，與Q級聯中的Qi相同，各組分的βi也不是任意的，必須滿足一定的約束關系。實際上，只要給定某組分(如關鍵組分)的組分分流因子，根據1個分離級的分離特性，可直接確定其余各組分的βi：

βi=γikβk

(20)

其中，k為關鍵組分的編號。應注意，這一關系不僅限于準理想級聯。

對式(17)、(18)、(19)的求解結果為：

(21)

準理想級聯由于計算簡單，也廣泛應用于多組分分離研究中。

2 三種模型級聯之間的聯系

首先要指出的是，式(5)、(14)、(21)在形式上明顯類似或完全相同，說明三種級聯之間可能有深層的聯系。

以往的研究也涉及對三種模型之間的關系分析。文獻[1]從Q級聯出發，得到了兩種組分相對豐度匹配的條件，指出由此可將Q級聯得到的組分豐度分布、總流量等結論應用于MARC。文獻[9]嘗試利用弱分離近似，證明Q級聯的組分分流比φi與準理想級聯的均為常數，從而將二者歸為一類，但其推導方法在級聯長度較長的情況下并不合適，仍有待商榷。文獻[10]引入組分分流因子的概念簡化三組分MARC的計算，但當時尚未有準理想級聯的概念，且也未進一步推廣到更多組分的情況。

本文將在以往研究的基礎上，分析總結三種模型級聯之間的相似處以及相互關系，更系統地建立三者之間的聯系。

2.1 準理想級聯與MARC

根據式(12)，MARC的任一級對于k、n兩組分均是對稱分離的，即：

(22)

根據組分分流因子的定義，有：

(23)

將式(23)代入式(22)，可得：

(24)

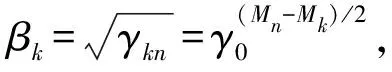
從另一角度看，對于準理想級聯，根據式(20)，指定關鍵組分的βk，其余的組分分流因子就都確定了，由于只要求βk>0，因此，可令：

(25)

其他組分的組分分流因子可寫成：

(26)

因此，所有組分分流因子均可由M*確定。

對于MARC，由式(24)可知：M*=(Mk+Mn)/2。因此，MARC只是準理想級聯的虛擬組分分子量取特定值時的一種特例。具體來說，M*取兩種組分分子量的算術平均值時，這兩種組分在各級之間滿足相對豐度匹配的條件，準理想級聯就成為了一MARC。

2.2 準理想級聯與Q級聯

準理想級聯與Q級聯的相似之處可非常明顯地從式(5)、(21)中看到。假如作如下對應：

SW→Nf，SP→N-Nf+1，βi→eQi

(27)

則兩種模型級聯的取料豐度的表達式完全一致。

進一步可證明在一定近似下，Q級聯也同準理想級聯一樣，具有常數的組分分流因子。以貧化段為例，在相鄰兩級之間，根據物質輸運關系，可得：

(28)

利用

(29)

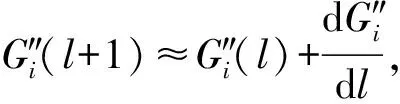
(30)

另外，從Q級聯的積分輸運方程(式(1))出發，可得到：

(31)

利用邊界條件

(32)

可求解式(30)，得到：

(33)

進而可得：

(34)

一般，ε0?1，而Mi與M*相差不大，故|Qi|?1，由式(34)近似可得：

(35)

由式(29)、(31)、(35)，可知：

(36)

這說明在近似情況下，Q級聯的各組分分流因子恒定為常數，與準理想級聯相同。

另外，在Q級聯中，同樣可引入類似于準理想級聯的虛擬組分分子量M*。根據式(4)，考慮εij的定義，可知：

Qi-Qj=ε0(Mj-Mi)

(37)

根據式(8)，式(37)一定得到滿足。

M*對Q級聯和準理想級聯均為重要的控制參數，其取值影響級聯的特性，因此，對Q級聯或準理想級聯的優化是針對M*進行的。但本文重點是比較研究不同的級聯，優化設計流程以及對M*參數范圍的設置可參考文獻[12，14]。從物理意義看，M*的取值決定了級聯對不同質量組分的分離特性，這在文獻中有分析，但由于其非常重要，在下面對此稍加解釋。

在Q級聯中，對于輕組分，Qi>0，根據式(36)，βi>1；而對于重組分，βi<1，這也與準理想級聯的規律一致。歸納起來，在準理想級聯或Q級聯中，輕組分經一個分離級后會更多地流向輕端，而重組分則相反，表明M*將所有組分劃為輕、重兩類，輕組分向著精料端被濃縮，而重組分向著貧料端被濃縮。但在精、貧料端獲得同樣的目標組分豐度下，M*的取值影響級聯的總流量(各級入口流量之和)。為取得最好分離效益，希望用最小的總流量取得同樣的分離效果，這樣，M*就成為一優化的參數，用來對MARC級聯[18]、準理想級聯[19]或Q級聯優化[11]。

Q級聯是一連續級聯，而準理想級聯卻是離散的，二者之間不是嚴格的對等關系，但已可確定這兩種模型級聯具有相似的特性，可視為同一類級聯模型。

當然，上面的分析也完全適用于描述Q級聯和MARC級聯之間的關系。

3 小結

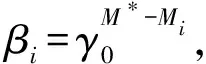
雖然Q級聯是一連續級聯，無法與準理想級聯完全等同，但分析可知，兩種級聯均可引入虛擬組分分子量M*，且其對于級聯的分離特性有相同的影響作用。更重要的是，與準理想級聯類似，Q級聯的組分分流比在近似條件下可視為常數。認為Q級聯和準理想級聯是相似的級聯模型是合理的。

因此，可將這三種模型級聯歸為一種級聯，根據實際情況針對一種級聯進行研究。

參考文獻：

[1] SULABERIDZE G A, BORISEVICH V D. Cascades for separation of multicomponent isotope mixtures[J]. Separation Science and Technology, 2001, 36(8-9): 1 769-1 817.

[2] de la GARZA A, GARRETT G A, MURPHY J E. Multicomponent isotope separation in cascades[J]. Chemical Engineering Science, 1961, 15(3): 188-209.

[3] SAZYKIN A A. Quasi-ideal cascades for separation of multicomponent isotope mixtures[C]∥Proceedings of 5th Scientific Conference on Physicochemical Processes in Selection of Atoms and Molecules. Zvenigorod, Russia: [s.n], 2000: 51-57.

[4] KUCHEROV R Y, MINENKO V P. Theory of cascades for separating multi-component isotope mixtures[J]. Soviet Atomic Energy, 1965, 19(4): 1 290-1 300.

[5] KOLOKOL′TSOV N A, MINENKO V P, NIKOLAEV B I, et al. Design of cascades for separating isotope mixtures[J]. Soviet Atomic Energy, 1970, 29(6): 1 193-1 198.

[6] 宋天明，曾實. 多組分氣體離心分離級聯的解析優化[J]. 清華大學學報：自然科學版，2006，46(12)：2 003-2 006.

SONG Tianming, ZENG Shi. Optimization of centrifuge cascades for the separation of multi-component gas mixtures[J]. Journal of Tsinghua University: Science and Technology, 2006, 46(12): 2 003-2 006(in Chinese).

[7] 謝全新，叢藝坤，邱志恒，等. 帶附加供料流和存在損耗的準理想級聯模型[J]. 同位素，2013，26(3)：180-185.

XIE Quanxin, CONG Yikun, QIU Zhiheng, et al. Model of quasi-ideal cascade with an additional feed flow and losses of working substances[J]. Journal of Isotopes, 2013, 26(3): 180-185(in Chinese).

[8] ZENG S, SMIRNOV A Y, JIANG D, et al. Isotopically selective mass transfer in the Q-cascade with losses of working substance[J]. Separation Science and Technology, 2013, 48(1): 15-21.

[9] ZENG S, SULABERIDZE G A, JIANG D, et al. The Q-cascade explanation[J]. Separation Science and Technology, 2012, 47(11): 1 591-1 595.

[10] YAMAMOTO I, KABA A, KANAGAWA A. Simple formulae for analyzing matched abundance ratio cascade with constant separation factors for multi-component isotope separation[J]. Journal of Nuclear Science and Technology, 1987, 24(11): 969-971.

[11] BORISEVICH V D, SULABERIDZE G A, ZENG S. New approach to optimize Q-cascades[J]. Chemical Engineering Science, 2011, 66(3): 393-396.

[12] ZENG S, YING C. A method of separating a middle component in multicomponent isotope mixtures by gas centrifuge cascades[J]. Separation Science and Technology, 2000, 35(14): 2 173-2 186.

[13] SMIRNOV A Y, SULABERIDZE G A, BORISEVICH V D. Influence of feed flow profile of cascade stages on the mass transfer of intermediate components[J]. Theoretical Foundations of Chemical Engineering, 2011, 44(6): 888-896.

[14] ZENG S, JIANG D, BORISEVICH V, et al. Use of the Q-cascade in calculation and optimization of multi-isotope separation[J]. Chemical Engineering Science, 2011, 66(13): 2 997-3 002.

[15] WOOD H G, BORISEVICH V D, SULABERIDZE G A. On a criterion efficiency for multi-isotope mixtures separation[J]. Separation Science and Technology, 1999, 34(3): 343-357.

[16] SULABERIDZE G A, BORISEVICH V D, XIE Q. Quasi-ideal cascades with an additional flow for separation of multicomponent isotope mixtures[J]. Theoretical Foundations of Chemical Engineering, 2006, 40(1): 5-13.

[17] YAMAMOTO I, KANAGAWA A. Multicomponent isotope separating cascade composed of elements with large separation factors[J]. Journal of Nuclear Science and Technology, 1978, 15(8): 580-584.

[18] von HALLE E. Multicomponent isotope separation in matched abundance ratio cascades composed of stages with large separation factors[C]∥Proceedings of 1st Workshop on Separation Phenomena in Liquids and Gases. Darmstadt, Germany: [s. n.], 1987: 325-356.

[19] SULABERIDZE G A, XIE Q, BORISEVICH V D. On some properties of quasi-ideal cascades with losses at stages[J]. Ars Separatoria Acta, 2006, 4: 467-477.