雙饋風力發電機組對電力系統穩定性的影響

武小梅，文福拴，劉國祥，歐英龍

(1.華南理工大學電力學院，廣州市 510641; 2.廣東工業大學自動化學院，廣州市 510006;3.浙江大學電氣工程學院，杭州市 310027; 4.廣東電網公司湛江供電局，廣東省湛江市 524005)

雙饋風力發電機組對電力系統穩定性的影響

武小梅1,2，文福拴3，劉國祥2，歐英龍4

(1.華南理工大學電力學院，廣州市 510641; 2.廣東工業大學自動化學院，廣州市 510006;3.浙江大學電氣工程學院，杭州市 310027; 4.廣東電網公司湛江供電局，廣東省湛江市 524005)

隨著雙饋感應風力發電機組(doubly-fed induction generators，DFIG)裝機容量在電力系統中所占比重的不斷增加,其與電力網絡之間的相互影響日漸增大。采用DIgSILENT軟件包對含有DFIG的電力系統的暫態穩定性進行了研究,并從Crowbar保護控制與電力網絡之間相互影響的角度探討了DFIG的Crowbar投切策略。首先研究了單臺DFIG的穩定性,然后以IEEE 30節點系統為例分析了在系統的同一節點分別接入DFIG型風電場和同步發電機組時系統的暫態穩定性;最后,從電力系統功角穩定性角度研究了Crowbar的最佳退出時間。結果表明,含DFIG型風電場的電力系統因短路電流降低使得繼電保護范圍縮小。

雙饋感應發電機； 暫態穩定；Crowbar；DIgSILENT軟件包

0 引 言

風力發電是最有前途的綠色能源之一,隨著雙饋感應風力發電機(doubly-fed induction generator, DFIG)裝機容量在電力系統中所占比重的逐步增長,其與電力網絡之間的相互影響趨于增大。因此,大型風電場(如 MW級雙饋型風電場)對電力系統穩定性的影響不容忽視。DFIG由于具有有功功率和無功功率獨立調節、勵磁變頻器所需容量小等優點,在風力發電系統中得到廣泛應用。目前，針對DFIG自身抵御電壓擾動能力較弱,實現低電壓穿越比較困難的缺點,廣泛采用了Crowbar硬件保護電路來保證DFIG的故障穿越能力。文獻[1]采用PSCAD驗證了Crowbar電路能夠提高DFIG的低電壓穿越能力。文獻[2]從DFIG功角動態行為角度分析其對系統穩定性的影響。文獻[3]認為與傳統鼠籠式風力發電機相比,DFIG具有更好的暫態穩定性。文獻[4]以美國西部電網WSCC 3機9節點簡化系統為例, 研究了在某些特定故障條件下,雙饋型風電場并網后對電力系統暫態穩定性產生的影響。文獻[5]提出通過計算特征值對慣性常數的靈敏度,來判斷DFIG對系統影響的性質。文獻[6]用時域仿真法證實DFIG和常規同步發電機組并列后,再經遠距離輸電線接入大系統后不會惡化系統穩定性。文獻[7]采用Matlab對交流勵磁風力發電機組的穩定性做了仿真分析,結果表明DFIG風電場能改善電力系統穩定性。文獻[8]以新英格蘭39節點系統為例,考察了DFIG高滲透功率比例(40%)對電力系統暫態穩定和頻率穩定的影響,研究表明:當故障發生在離風電接入點較近位置時,由于DFIG的Crowbar動作,風電在有功功率大量減少的同時吸收大量無功功率,會對暫態穩定性產生不利影響；當故障發生在離同步電機較近位置時,暫態穩定性有所改善。現有文獻的研究表明,在雙饋機組對電力系統穩定性影響方面尚沒有一致的結論,原因在于不同文獻所采用的雙饋機組數學模型、參數不同,控制策略和控制參數也有差異。但是,這些文獻都反映了系統總機械慣性降低和頻率響應變差的問題。

本文從DFIG自身穩定性出發研究其對同步發電機組的影響,并且以IEEE30節點系統為例,研究了DFIG對電力系統暫態穩定和頻率穩定的影響,最后從功角穩定的角度考察了Crowbar的最佳退出時間。

1 雙饋風力發電機暫態模型及控制策略

在國內外現有的風電并網運行導則中,多數要求風電機組必須具備低電壓穿越 (low voltage ride through, LVRT)能力。Crowbar保護電路退出時間對雙饋風電機組的LVRT能力有很大的影響[9-12]。文獻[9-11]都是針對單臺DFIG的暫態響應來分析Crowbar的退出時間的。文獻[9]指出Crowbar電路投入時間不應太長;文獻[10-11]則指出Crowbar在短路故障切除之前退出運行,且退出運行的時刻盡可能接近短路故障切除時刻;文獻[12]建議Crowbar投入后應在故障清除后1～2個周波內切除;文獻[13]則提出采用無功判定法檢測短路故障切除時間,實現故障切除后立刻退出Crowbar電路的策略。

假定定子和轉子三相繞組對稱且不考慮0軸分量, 則旋轉d-q坐標系下DFIG的數學模型可作如下描述[14]。

磁鏈方程:

ψsd=Lsisd+Lmird

(1)

ψsq=Lsisq+Lmirq

(2)

ψrd=Lrird+Lmisd

(3)

ψrq=Lrirq+Lmisq

(4)

式中:ψ、i、L為繞組的磁鏈、電流、電感;下角標s表示定子,r表示轉子，m表示互感。

電壓方程:

(5)

(6)

(7)

(8)

式中:U為繞組的電壓；s為電機的轉差率；ω為坐標系旋轉角速度；Rs、Rr分別為定、轉子的電阻。

電磁轉矩方程和運動方程:

Te=npLm(isqird-isdirq)

(9)

(10)

式中:Te為電磁轉矩;np為電機的極對數;ωr為轉子旋轉角速度;TL為風力機提供的驅動轉矩;J為風力機的轉動慣量。定子有功功率和無功功率分別為

(11)

(12)

DFIG的變流器控制系統用于實現轉子側變流器控制和系統側變流器控制。DFIG的變流器通常采用雙環雙PI控制，轉子側變流器的功率外環生成快速電流內環控制的電流參考值(d軸、q軸分量),電流內環控制轉子電流,以實現有功功率和無功功率的控制。系統側的變流器控制也采用雙環雙PI控制,直流電壓外環同樣產生其電流內環控制所需的電流參考值,而內環電流控制的d軸分量可實現轉子與系統的無功交換控制,q軸分量可控制直流電壓環節的電壓處于設定值附近。

2 雙饋風力發電機穩定性分析

DFIG穩定性指單臺DFIG機組接入無窮大系統時的穩定性問題。DFIG異步運行,其轉子轉速可以通過改變交流勵磁電源的頻率進行調節,具有廣泛的穩定運行范圍,其在任一滑差的運行點上具有與傳統同步發電機相同的功角特性方程[15]：

(13)

式中:E為發電機內電勢,U為無窮大母線電壓,XΣ為E到U的轉移電抗。同步發電機的搖擺方程為關于功角的非線性二階微分方程:

(14)

式中:T為發電機組的慣性時間常數;D為阻尼系數;PT為原動機輸出的機械功率。DFIG由于機電解耦, 其轉子運動方程是關于轉速的一階微分方程：

(15)

式中:Pw為風力機輸出機械功率;ωg為風機的角速度。由于DFIG的功角和轉速不存在積分關系,即 dδ/dt≠ωg,故不存在類似于同步發電機的動力學失穩問題。但是,由于DFIG采用了雙閉環勵磁調節,再加上DFIG的廣義Park方程是非線性高階微分方程[16],因此，存在電磁暫態下的動力學穩定性問題。

為了說明上述觀點,在DIgSILENT軟件中搭建2 MW DFIG接于無窮大系統的模型, 并經0.69 kV/20 kV和20 kV/110 kV 2臺升壓變壓器接入110 kV無窮大系統,如圖1所示。

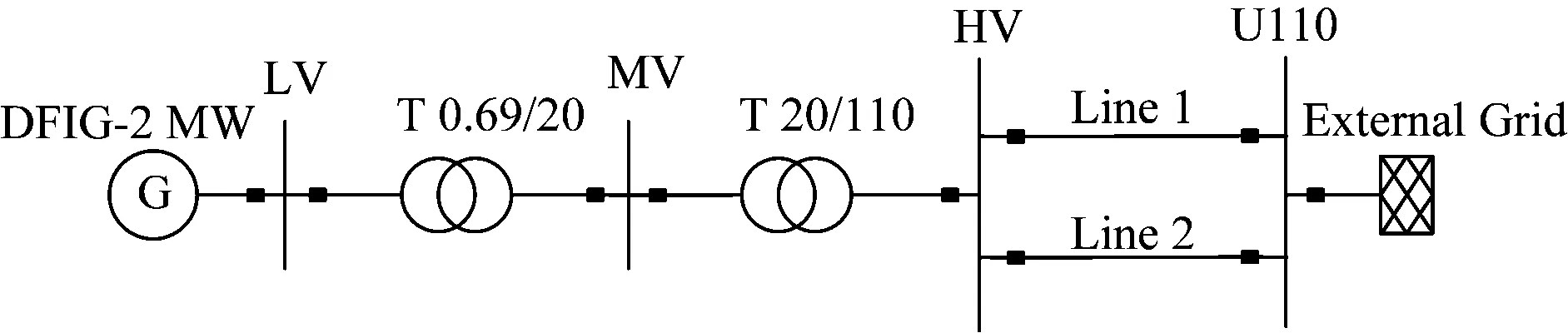
圖1 接入DFIG的單機無窮大系統

雙饋發電機參數如下:極對數np=2;額定有功容量和額定無功容量分別為2 MW和0.25 Mvar;定子額定電壓為0.69 kV;額定頻率f=50 Hz；定子側采用Δ接法,以發電機額定容量為基準，定子電阻為0.005 9 pu,定子漏抗為0.079 0 pu;轉子側采用Y接法,轉子電阻為0.006 2 pu,轉子漏抗為0.112 0 pu;互感電抗為3.9 pu。在t=2 s時Line2線路上發生三相短路故障,2.6 s 后故障清除且線路重合閘重合成功,故障發生時風速保持恒定。

圖2是故障前后的DFIG定子有功功率和無功功率響應曲線。由圖可知,故障導致定子有功功率和無功功率發生劇烈振蕩,當故障清除后經過大約1.3 s 后定子有功功率和無功功率又恢復到初始值,系統最終恢復了穩定。由圖3可知,遭受擾動后的DFIG在機械轉矩不變的條件下,其轉速發生大范圍波動,但沒有出現動力學失穩現象。

因此,DFIG自身沒有機電暫態失穩現象,也不存在其與系統中的同步發電機之間失步問題。此外,研究發現,當DFIG的定、轉子繞組的電阻減小時,電磁模式阻尼變小,可能出現電磁暫態失穩現象。

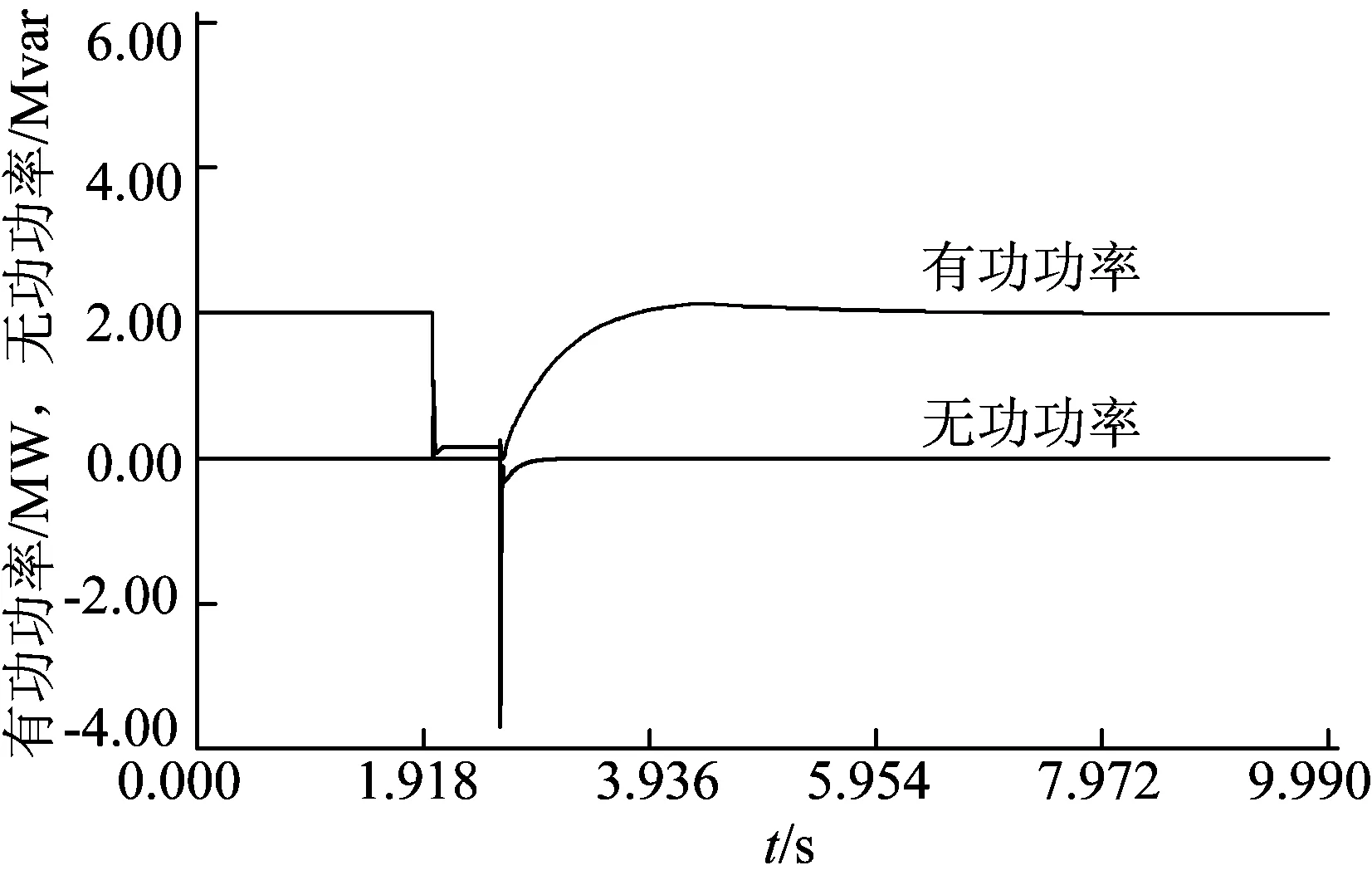
圖2 DFIG定子有功功率和無功功率暫態響應波形

圖3 DFIG轉子轉速的暫態響應波形

3 并列運行的DFIG對系統運行穩定性的影響

3.1 DFIG對系統短路容量的影響

電力系統暫態穩定是指系統遭受大擾動后,能從原來的運行狀態不失同步地過渡到新的穩定運行狀態的能力。風力發電機組作為一種電源,在系統發生短路故障后,也會向故障點輸送短路電流。短路容量主要用來校驗開關的切斷能力,若斷路器在短路時遮斷容量不夠,會引起斷路器的爆炸。

圖4為一個簡單電力系統,在進行等值網絡變換后,可求出系統的總阻抗XΣ*。當發生三相短路時,短路容量計算公式為

(16)

(17)

式中:Uav為短路處正常工作電壓的平均值;IK為流過斷路器的短路電流有效值；SB為基準功率；UB為基準電壓。如果同步發電機組G2被風機替換,則從20 kV側等效電路來看系統中總阻抗將變大,因為從風機出口電壓0.69 kV折算到20 kV側時其阻抗需乘以K2=(V20/V0.69)2,此時風機和相應的內部集電線路相當于一個很大的限流電抗,短路電流就會變小,因此斷路器的遮斷容量就需要重新整定。

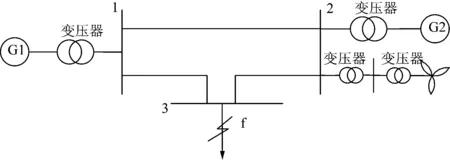
圖4 簡單電力系統的單線圖

在DIgSILENT軟件環境中搭建IEEE 30節點系統, 其參數及接線圖見文獻[17]。在IEEE 30節點系統中,發電機G1為平衡節點,假設該系統中G1、G2、G13分別為常規火電機組,系統的基準容量為100 MVA;G5、G8、G11分別接雙饋型風電場,風電機組采用恒功率因數控制,定子出口額定電壓為0.69 kV,其穿透功率為27.3%;系統中同步發電機模型采用計及交直軸次暫態電抗、交直軸暫態電抗的六階模型,并考慮了勵磁調節系統、調速系統的作用;負荷模型采用恒阻抗模型,負荷水平為283.4 MW。定義無風電接入的原系統為系統①，接入風電后為系統②,分別進行三相短路電流計算,結果如表1所示。

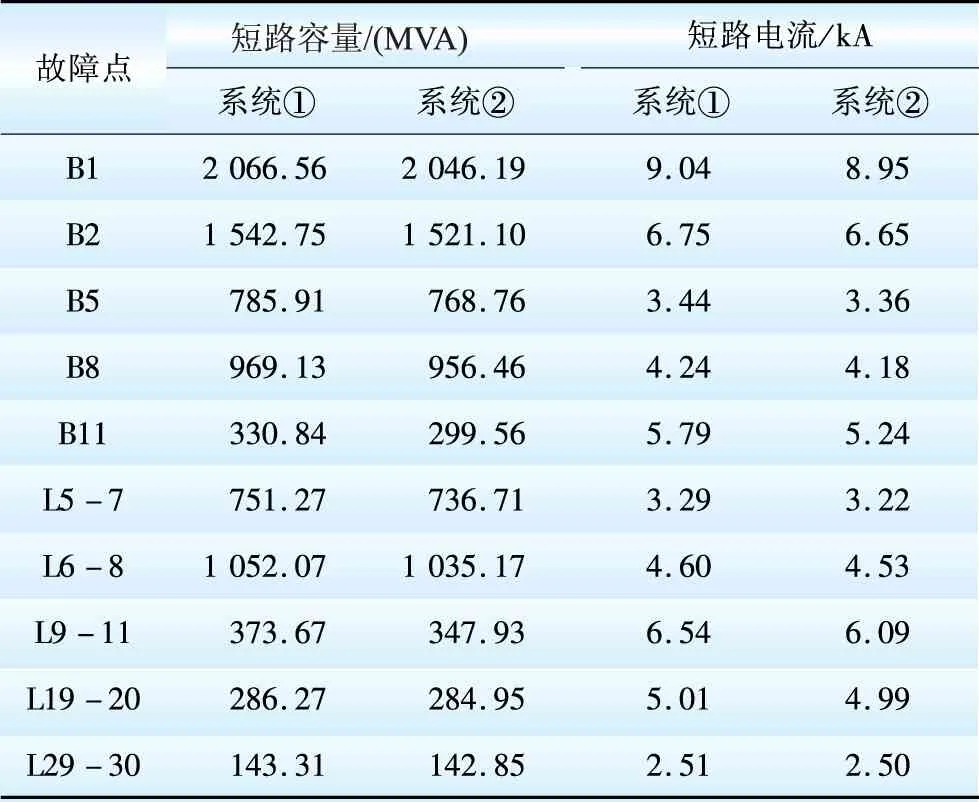
表1 2個系統發生三相短路時短路電流計算結果比較

從短路電流計算結果可知:系統接入風機后,短路容量和短路電流都降低,不會出現斷路器在短路時遮斷容量不足的問題,但是系統原來的保護定值已不能滿足要求,所以需對系統原保護定值進行重新核算。如果按照之前設定的保護定值運行,則在系統發生短路后,由于線路上流過的短路電流隨著大容量風電場的接入而減小很多,這使得保護范圍縮小,這樣線路上就會出現保護拒動,從而對電力系統穩定性產生不利影響。可以采用自適應繼電保護解決風電引起的電網保護問題,因為這種保護能夠根據系統運行方式和故障狀態的變化而實時改變保護性能、特性或定值[18]。

3.2 DFIG對系統頻率的影響

隨著大量風力發電接入系統,對系統穩定性可能產生影響。可以從系統發生擾動和風電場發生擾動2個方面進行頻率穩定性分析。對于系統發生擾動情形采用時域仿真法,針對IEEE 30節點系統①和系統②分析風電與系統之間的相互影響。

在仿真時,設置時間t=20 s時,同步發電機G13發生故障退出運行,假定仿真過程中風速不發生變化,仿真結果如圖5、6所示。圖5為系統頻率響應特性曲線,圖6為系統頻率偏差曲線。

由圖5、6的仿真結果可知,在系統發生有功功率缺額時,系統①和系統②的頻率最后分別穩定在49.862 Hz和49.829 Hz,其頻率偏差分別為-0.138 Hz和-0.171 Hz;在系統發生有功功率缺額而導致的頻率下降過程中,同步發電機組能提供頻率支持作用,即在其調速系統作用下能提供持續的有功出力,從而能夠很好地維持頻率穩定。對于DFIG而言,其控制系統使其發電機轉速與系統頻率完全解耦控制,在系統頻率變化時,風電機組不能及時響應,因此會導致整個系統慣量降低,所以當系統中的雙饋機組穿透功率較大,系統有功功率缺額較大時,不利于系統的頻率穩定。

圖5 系統頻率響應特性曲線

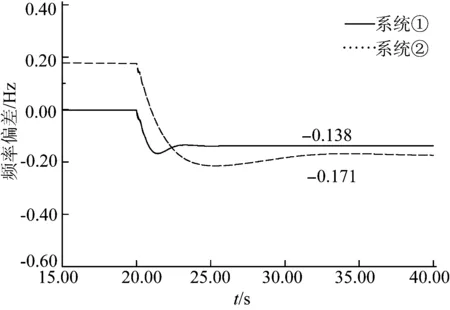
圖6 系統頻率偏差曲線

3.3 Crowbar保護退出時間對系統穩定的影響

低電壓穿越能力是風電并網要求的核心內容之一,Crowbar保護是針對DFIG特別設計的,用來保護轉子側變流器,防止其出現過電流而損壞。當轉子電流超出設定的閾值時,投入Crowbar電路,為轉子過電流提供一條通道,即阻塞變流器以取得保護效果。

這里以IEEE 30節點系統②為例,從Crowbar的不同退出時間與系統的交互影響角度進行分析。給定8號母線在1 s時發生三相短路故障,1.3 s時故障切除; 故障發生后,8號母線所接DFIG的Crowbar保護電路立刻投入,這里分析Crowbar分別在下面3種工況下對同步發電機的功角特性、有功功率、勵磁電壓的影響:(1)故障發生時投入, 故障清除前切除;(2)故障發生時投入,故障清除后立即切除;(3)故障發生時投入,故障清除后繼續運行一段時間再切除。下面分別給出系統頻率曲線(圖7)和G2的功角特性、有功功率、勵磁電壓的波動曲線(分別見圖8、9、10)，及故障清除后Crowbar繼續運行一段時間G2的功角特性波動曲線(圖11)。

由圖7～10可知, Crowbar在故障清除前切除和故障清除后立即切除這2種情況下其各曲線的波動情況基本一致, 且都比Crowbar在故障清除后繼續運行一段時間再切除波動范圍大。例如, 圖7中Crowbar在故障清除前切除, 系統頻率最后穩定在49.819 Hz; Crowbar在故障清除后立即退出, 系統頻率最后穩定在49.822 Hz; 故障清除后繼續運行一段時間再切除, 頻率最后穩定在49.889 Hz。

圖7 在不同的Crowbar退出時間下頻率響應特性曲線

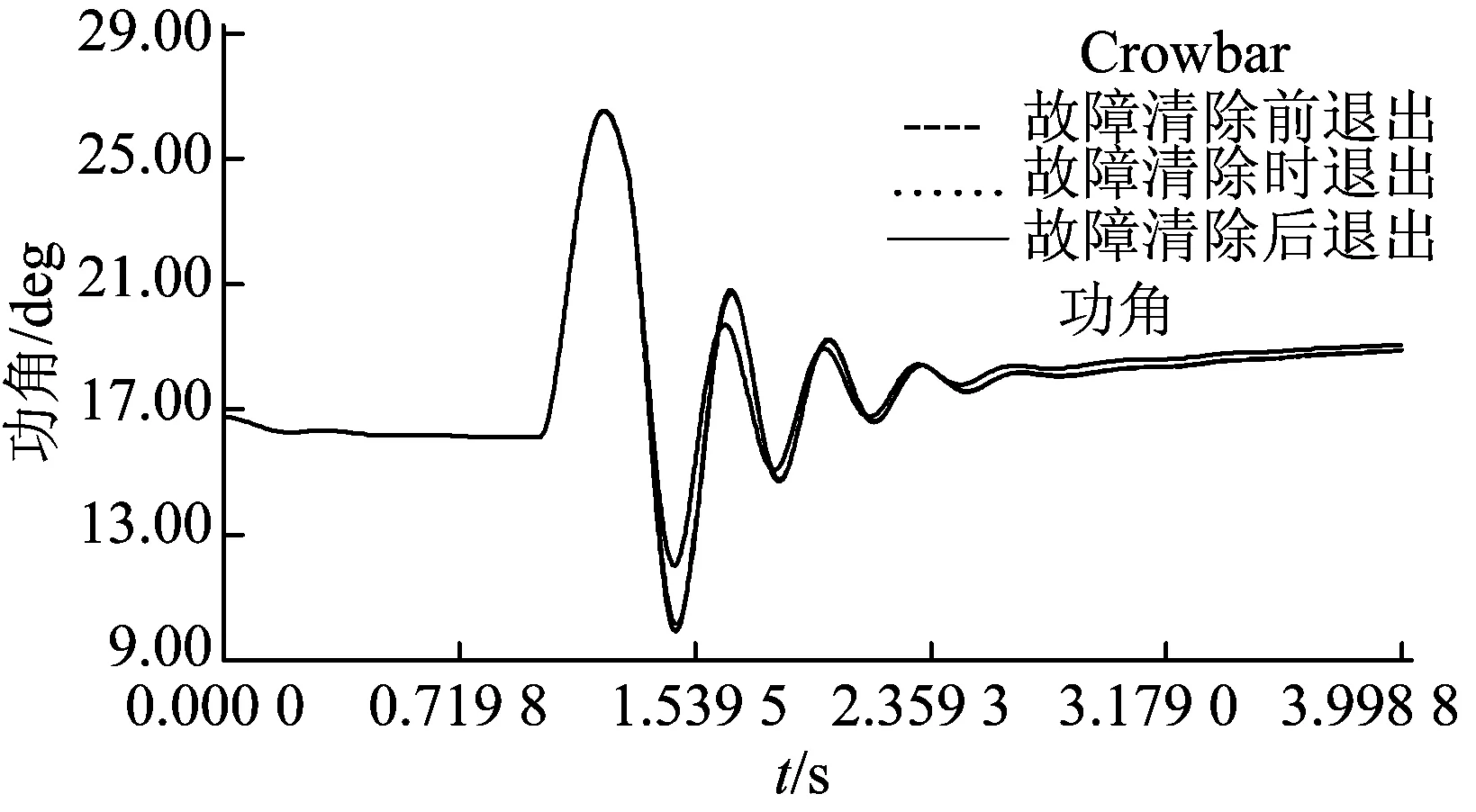
圖8 在不同的Crowbar退出時間下G2的功角波動曲線

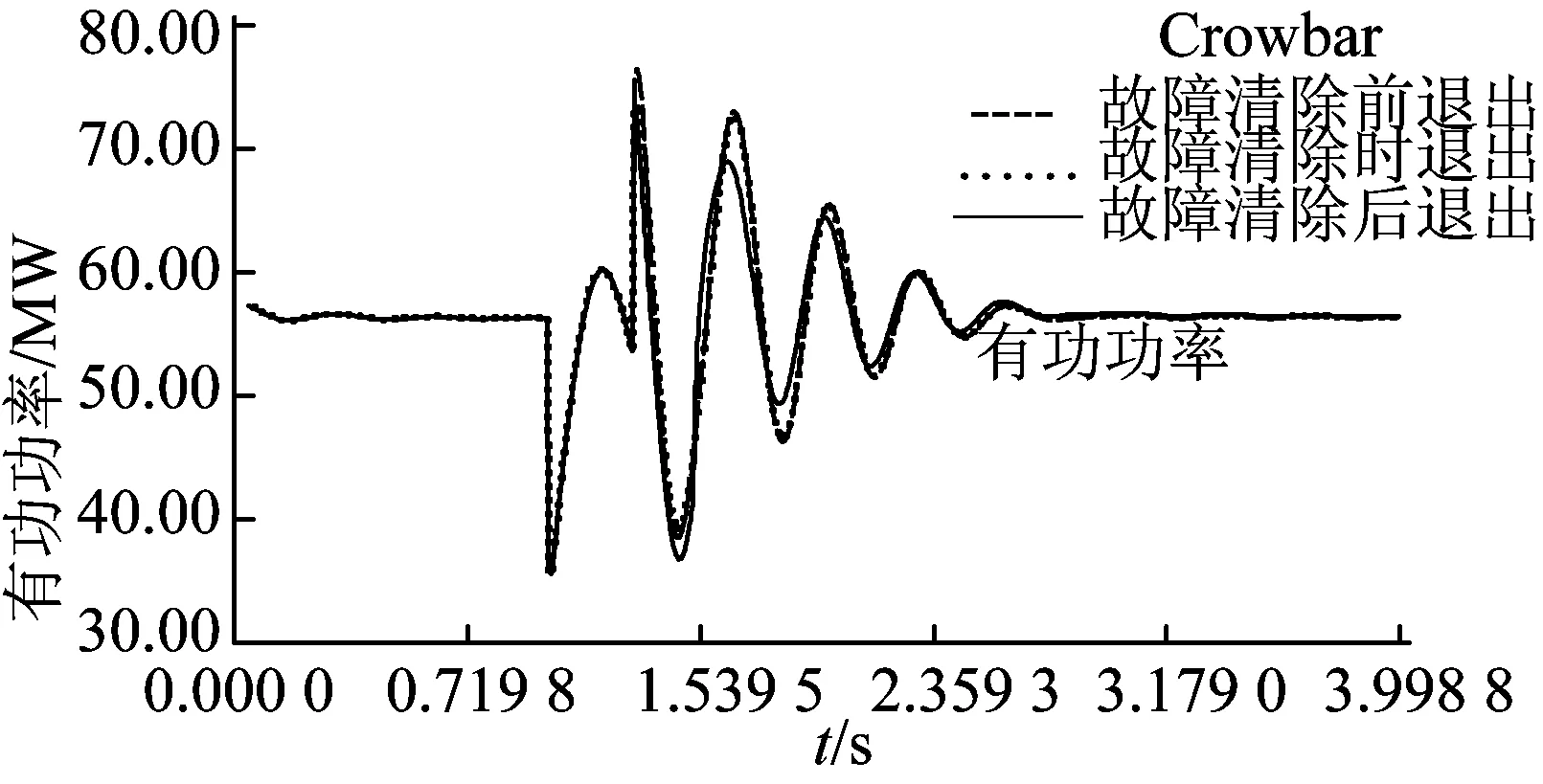
圖9 在不同的Crowbar退出時間下G2的有功功率波動曲線

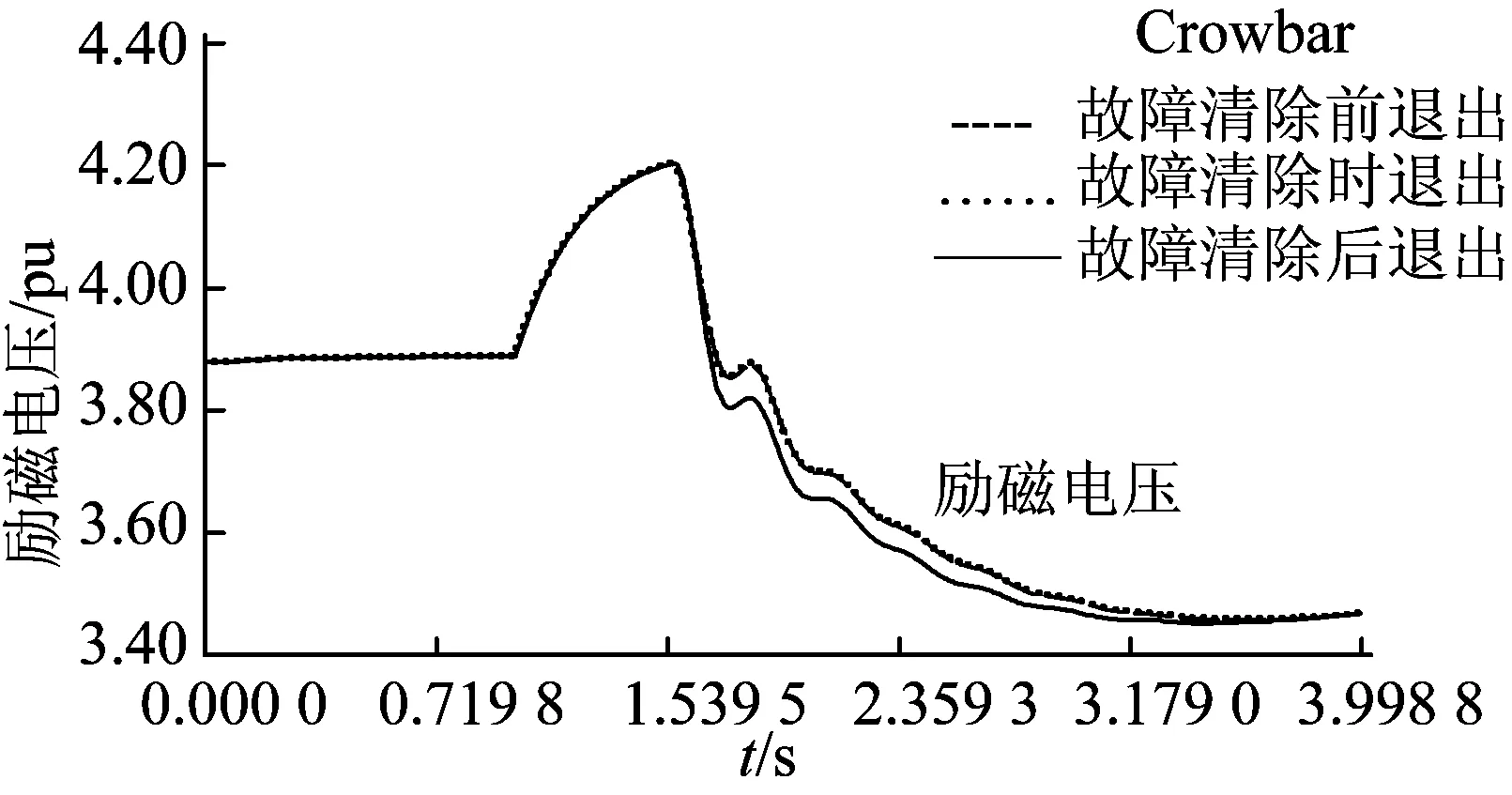
圖10 在不同的Crowbar退出時間下G2的勵磁電壓波動曲線

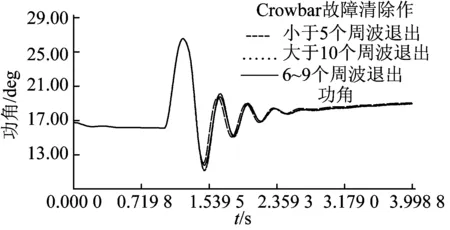
圖11 故障后在不同的Crowbar退出時間情形下G2的功角波動曲線

由圖8可知, Crowbar在故障清除后繼續運行一段時間再切除時, 功角波動范圍較小。由圖11可知, Crowbar在故障清除后6～9個周波再切除時, 功角波動范圍最小。

4 結 論

本文研究了DFIG對電力系統暫態穩定性、頻率穩定性的影響以及Crowbar保護不同退出時間對系統穩定性的影響, 并以IEEE 30節點系統為例做了仿真分析, 得到如下結論:

(1)對于DFIG單機接無窮大系統, 仿真結果表明, DFIG自身沒有機電暫態失穩現象, 也不存在DFIG與同步發電機的失步問題。

(2)含DFIG的電力系統短路電流計算結果表明, 由于DFIG引起短路電流減小, 從而使得繼電保護范圍縮小，線路上會出現保護裝置拒動, 對系統穩定性產生不利影響。

(3)在DIgSILENT中建立了含有DFIG的30節點系統模型, 其中風電穿透功率達到27.3%。當系統中的DFIG穿透功率較大, 系統有功功率缺額較大時, 不利于系統的頻率穩定。最后, 從功角穩定性角度驗證了Crowbar在故障清除后繼續運行6～9個周波再切除效果最佳。

[1]LIMA F K A. Rotor voltage dynamics in the doubly fed induction generator during grid faults[J]. IEEE Transactions on Power Electronics, 2010, 25(1), 118-130.

[2]郝正航, 余貽鑫. 雙饋風力發電機組對電力系統穩定性影響[J].電力系統保護與控制, 2011, 39(3): 7-11.

[3]趙清聲, 王志新. 雙饋風力發電機組系統接入與穩定運行仿真[J]. 電網技術, 2007, 31(22): 69-74.

[4]石立寶, 戴世強. 大規模雙饋型風電場并網的系統暫態穩定仿真[J]. 電力系統及其自動化學報, 2009,11(4): 1-6.

[5]Gautam D, Vittal V, Harbour T. Impact of increased penetration of DFIG-based wind turbine generators on transient and small signal stability of power systems[J]. IEEE Trans on Power Systems, 2009, 24(3): 1426-1434.

[6]Muljadi E, Butterfield C P, Parsons B, et al. Effect of variable speed wind turbine generator on stability of a weak grid[J]. IEEE Trans on Energy Conversion, 2008, 22(1): 29-35.

[7]閆廣新,吐爾遜,晁勤.交流勵磁雙饋風力發電機組的穩定性仿真分析[J].繼電器,2007,35(14):7-9.

[8]Meega H L, Flynn D. Impact on transient and frequency stability for a power system at very high wind penetration[C]//IEEE Power and Energy Society General Meeting, Minneapolis:IEEE,2010: 1-6.

[9]姜傳,肖湘寧.應用撬棒電路的雙饋型風力發電機低電壓穿越分析[J].電網與清潔能源,2012,28(1):80-83.

[10]張靠社,王媛,胡德海.基于Crowbar保護的雙饋感應發電機組的低電壓穿越研究[J].電網與清潔能源,2011,27(10): 66-70.

[11]朱曉東,石磊,陳寧,等.考慮Crowbar 阻值和退出時間的雙饋風電機組低電壓穿越[J].電力系統自動化,2010,34(18): 84-89.

[12]徐殿國,王偉,陳寧.基于撬棒保護的雙饋電機風電場低電壓穿越動態特性分析[J].中國電機工程學報,2010,30(22):29-36.

[13]李鴻儒,金煒東,胡立錦,等.基于無功判定法的Crowbar 保護電路退出控制[J].電力系統保護與控制,2012,40(15):99-103.

[14]賀益康,胡家兵,徐烈.并網雙饋異步風力發電機運行控制[M].北京:中國電力出版社,2011.

[15]陳樹勇,陳會員,唐曉駿,等.風火打捆外送系統暫態穩定切機控制[J].電網技術,2013,37(2):514-519.

[16]高景德,王祥珩,李發海.交流電機及其系統的分析[M].北京:清華大學出版社, 2005.

[17]劉明波,謝敏,趙維興.大電網最優潮流計算[M].北京:科學出版社,2010.

[18]沈冰,何奔騰,張武軍.新型自適應距離繼電器[J].電力系統自動化,2007,31(7):39-44.

(編輯：張小飛)

ImpactofDoubly-FedInductionGeneratoronPowerSystemStability

WU Xiaomei1,2, WEN Fushuan3, LIU Guoxiang2, OU Yinglong4

(1. School of Electric Power, South China University of Technology, Guangzhou 510641, China;2. Faculty of Automation, Guangdong University of Technology, Guangzhou 510006, China;3. College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China;4. Zhanjiang Power Supply Bureau, Guangdong Power Grid Corporation, Zhanjiang 524005, Guodong Province, China)

With continuous increase of installed capacity of doubly-fed induction generators (DFIG)in power systems, the interaction between DFIG and power system is becoming more significant. This paper studied the transient stability of power system containing DFIG with using software package DIgSILENT, and discussed the switching strategy of Crowbar for DFIGs through investigating the interactions between the Crowbar protection/control and the power system. First, the stability of a single DFIG was investigated. Then, taking IEEE 30-bus system as example, the transient stability of a scenario with a DFIG wind farm or a synchronous generator respectively connected to a same bus was analyzed. Finally, the optimal exit time of Crowbar was studied form the aspect of power angle stability. The results show that the short-circuit current of the power system containing DFIG wind farm is reduced, so the range of the protective relay can be decreased.

doubly-fed induction generator; transient stability; crowbar; software package DIgSILENT

國家高技術研究發展計劃(863計劃)資助項目(2011AA05A105)；廣東省電力節能與新能源技術重點實驗室資助項目(ZDSYS200701)；廣東電網公司2012年科技項目(K-GD2012-218)。

TM 315

： A

： 1000-7229(2014)06-0007-06

10.3969/j.issn.1000-7229.2014.06.002

2013-12-14

：2014-03-21

武小梅 (1972), 女, 博士, 副教授, 主要研究方向為電力系統運行分析與控制以及新能源發電，E-mail: eexiaomei@126.com;

文福拴 (1965), 男, 特聘教授, 博士生導師, 主要研究方向為電力系統故障診斷與系統恢復、電力經濟與電力市場、智能電網與電動汽車，E-mail: fushuan.wen@gmail.com。