活動時間不確定性的網絡計劃計算問題研究★

張 海 濤

(江漢大學機電與建筑工程學院，湖北 武漢 430056)

活動時間不確定性的網絡計劃計算問題研究★

張 海 濤

(江漢大學機電與建筑工程學院，湖北 武漢 430056)

對網絡計劃中應用最為廣泛的PERT模型在理論上和實踐中反映的誤差作了討論，將L-R模糊數引入到網絡計劃中，建立了模糊關鍵線路法模型及其模糊時間參數計算方法，提出了可以采用模糊數大小排序的方法比較各線路的模糊工期，從而方便地確定關鍵線路。

PERT網絡，模糊網絡，L-R三角模糊數，關鍵線路

0 引言

在土木工程中應用最為廣泛的網絡模型是關鍵線路法(CMP)和計劃評審技術(PERT)，兩者都以網絡圖為基本模型，不同之處在于前者的活動時間是肯定型參數(一個較肯定的估計值)，后者的活動時間是非肯定型參數(假設符合一定分布的時間隨機變量)。在大多情況下，將活動時間作為肯定的估計值是困難的，如在施工過程活動時間會受天氣的影響。對這種具有不確定活動時間問題的處理用PERT方法在實際應用中非常成功，但是，PERT方法的成功并不是因為其模型在理論上的完善，而是因為工程項目的進度計劃管理工作是一個動態的過程，一旦發現有偏離計劃的情況就及時糾正，糾正手段包括提供必要的資源、改變工作順序、采用新的技術等。

從理論上看PERT方法并不健全。這一方面是由于PERT方法本身的假設會產生較大的誤差，有關研究表明：根據其假設得出的平均項目時間幾乎總是小于實際統計時間；另一方面是對活動時間不確定性描述的片面性。網絡計劃模型中具體活動時間的不確定源于三種不確定性(隨機性、不知性、模糊性)，僅僅考慮其隨機性是不全面的[1]。文獻[1]同時認為描述這種不確定性的最好方法是使用模糊數學的概念和方法。

1 隨機性網絡的局限性

1.1 PERT方法的假定[2，3]

1)每項工程都有分解為有限數量的活動，這些活動是相互獨立的，各自具有明確的內容和起止界限；

2)每項活動的周期是PERT活動網絡中的獨立隨機變量，具有一定的概率分布和統計特征；

3)活動周期均服從β分布，其期望值、方差近似地分別按式(1),式(2)計算：

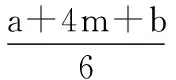
(1)

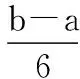
(2)

其中，a，m，b分別為活動ij的樂觀時間、最可能時間、悲觀時間。

4)設關鍵線路上具有足夠多的活動，因而中心極限定理可用于工程周期的概率計算；

5)網絡中只有一條線路占支配地位，其他路線成為關鍵線路的概率可以忽略不計。

根據上述假定，為了應用PERT，需要求出三個參數a，m和b的最優估計值，用這些參數計算期望值和方差，并確定關鍵線路和計劃延續時間的概率估計。

PERT模型過分依賴于上述假設和簡化及三個參數a，m和b的假設，即這三個參數可以由專家為網絡的每個活動收集得到[3]。

1.2PERT假定產生的誤差

首先，沒有任何經驗證明活動周期分布函數的最合適形式是β函數；其次，眾所周知，兩個或兩個以上的正態分布量的最大值不是正態分布。而且，如Clark指出的那樣，即使可以認為這個最大值是一個正態分布量，但其期望值和方差再不是式(1)和式(2)的形式[3]。

對于應用式(1)和式(2)計算的期望值和標準離差的誤差，文獻[4]中提到均值約為33%，標準離差約為17%。文獻[5]的研究表明，根據以上假定得出的平均項目時間幾乎總是小于實際統計平均值，誤差可達30%。另外，文獻[3]的研究表明，即使單個線路服從正態分布，而工程工期服從正態分布的條件是網絡中只有一條線路占支配地位的假設必須成立，但實際工程中，往往要同時考慮幾條關鍵線路。

2 模糊網絡模型的建立

2.1 網絡時間參數的計算

網絡圖時間參數的計算內容包括：各項工作的最早可能開始時間、最早可能完成時間、最遲必須開始時間、最遲必須完成時間、各項工作的各類時差以及工期等。

1)最早可能開始時間的計算。

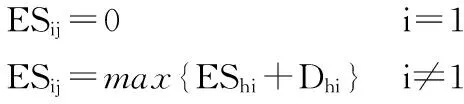
(3)

其中,EShi為工作ij的各項緊前工作hi的最早可能開始時間；Dhi為工作ij的各項緊前工作hi的持續時間。

2)最早可能完成時間的計算。

EFij=ESij+Dij

(4)

3)網絡計劃計算工期的計算。

TC=max{EFin}

(5)

其中,n為終點節點。

4)最遲必須完成時間的計算。

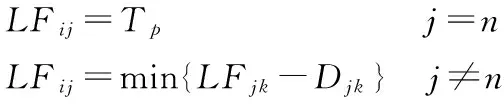
(6)

其中,Tp為計劃工期(當已規定了要求工期Tr時，Tp≤Tr；當未規定要求工期時，Tp=TC)；LFjk為工作ij的各項緊后工作jk的最遲必須完成時間；Djk為工作ij的各項緊后工作jk的持續時間。

5)最遲必須開始時間的計算。

LSij=LFij-Dij

(7)

6)總時差的計算。

TFij=LSij-ESij=LFij-EFij

(8)

7)自由時差的計算。

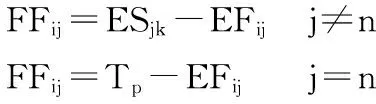
(9)

2.2 L-R三角模糊數的網絡修正運算

(10)

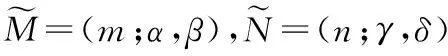
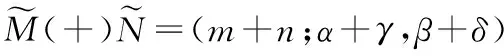
(11)

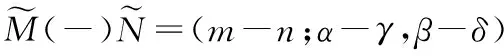
(12)

其中：

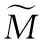
(13)

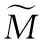
(14)

2.3 關鍵線路的判斷及工期實現的可能性計算模型

從線路上總的工作持續時間最長的線路為關鍵線路這一關鍵線路定義出發，應用模糊數排序的方法，比較每條線路的模糊計算工期，工期模糊數最大的線路應為關鍵線路。

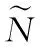
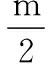
(15)

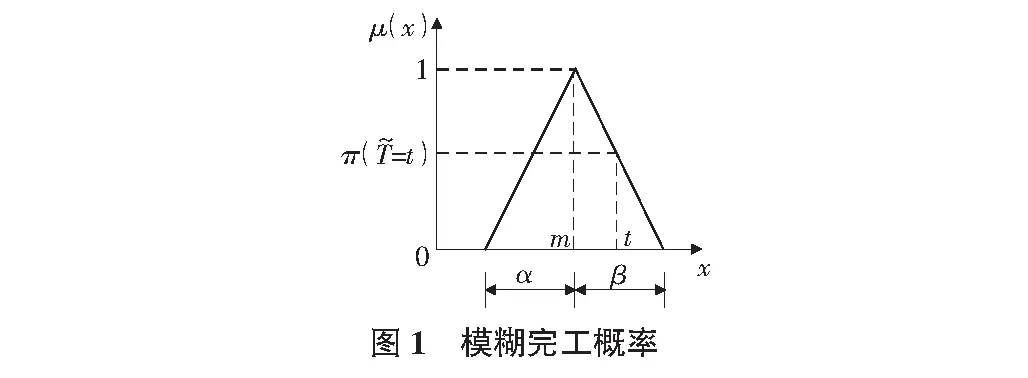
為了計算在給定工期下工程完工的可能性，定義在給定工期t(普通的實數)下工程完工的概率為[6]:

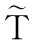
(16)

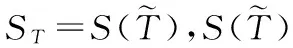
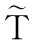
(17)

式(17)可參見圖1，其含義為三角形被t所截得到的左邊圖形的面積同原三角形的面積之比。

3 結語

1)諸多研究表明PERT隨機模型在理論和方法上都有其局限性。

2)在網絡計劃中采用模糊集合論的原理在一定程度上綜合了模糊性、隨機性以及不可知性。

3)修正后的模糊數運算規則可以使網絡時間參數計算成為可能。

4)在施工網絡中引入模糊數學的觀點，正成為一個研究方向，隨著模糊理論的進一步發展，其在實踐中的應用將成為可能。

[1] 李若剛.關于網絡計劃模型中的時間不確定性的討論[J].系統工程與電子技術，1997(8)：40-45.

[2] 馮允成.活動網絡分析[M].北京：北京航空航天大學出版社，1991.

[3] S. E.埃爾曼夫拉比.網絡計劃模型與控制[M].北京：機械工業出版社，1987.

[4] 江景波.網絡計劃技術[M].北京：冶金工業出版社，1983.

[5] K.R.MacCrimmon,C.A.Ryavec.An analytical study of the PERT assumption[J].Opns.Res.，1964(12)：6-17.

[6] Cynthia S. M. Use PERT as an approximation of fuzzy project-network analysis[J].IEEE Transactions on Engineering Management，1993，40(2)：146-153.

[7] 聶相田.基于模糊網絡進度計劃的工程完工風險評價[J].人民黃河，2012，34(5)：112-116.

[8] 褚春超.復雜工序關系的模糊網絡計劃分析與建模[J].天津大學學報，2006，39(5)：631-635.

Research on the algorithm of network plan based on the uncertainty of the activity time★

ZHANG Hai-tao

(School of Electromechanical & Architectural Engineering, Jianghan University, Wuhan 430056， China)

This paper discusses the defections of PERT model on theory and practice, after usingL-Rfuzzy number to describe activity time, the model of identifying fuzzy critical path is found, and the algorithm of fuzzy time parameters is presented. Then, this article presents that it is effective and easy to identify the critical path through ranking method of fuzzy number.

PERT network， fuzzy network，L-Rtriangular fuzzy number， critical path

1009-6825(2014)18-0267-02

2014-04-15 ★：江漢大學資助項目(項目編號：機建J2008[2013])

張海濤(1970- )，男，博士，副教授

TP393

A