北斗衛星18參數廣播星歷擬合中關于調和項的影響分析

王 樂，賈小林，范麗紅，李 麗，張愛能

(1．長安大學 地質工程與測繪學院，陜西 西安 710054；2．西安測繪研究所，陜西 西安 710054)

北斗衛星18參數廣播星歷擬合中關于調和項的影響分析

王 樂1，賈小林2，范麗紅1，李 麗1，張愛能1

(1．長安大學 地質工程與測繪學院，陜西 西安 710054；2．西安測繪研究所，陜西 西安 710054)

根據GPS最新的ICD文檔定義的18參數廣播星歷模型，分別推導在考慮調和項和忽略調和項的情況下各個參數的偏導數公式，且對參數ΔA偏導數的簡化進行定量分析，并通過北斗MEO衛星定軌數據對忽略調和項和簡化ΔA偏導數后的擬合算法進行測試，結果說明采用忽略調和項的偏導數和經過簡化后ΔA偏導數對擬合精度基本沒有影響。

廣播星歷18參數；調和項；偏導數；最小二乘法

衛星實時定位是以衛星實時發布廣播星歷為基礎的，然而廣播星歷的獲得是通過一系列已知時刻的坐標和速度采用相關的擬合算法擬合而成，對于廣播星歷擬合算法的精度和工作效率一直是研究的熱點問題。在GPS最新發布的ICD(Interface Control Document)文檔中重新定義了一組18參數廣播星歷[1-2]，這與之前所采用的16參數廣播星歷有所不同，那么針對這組新的廣播星歷參數，需要建立各參數和已知點之間新的線性函數模型，推導三維坐標對于新參數的偏導數。然而由于參數個數較多，直接推導的偏導數表達式較為復雜，為了簡化偏導數公式，有必要研究調和項與參數偏導數之間的關系和對參數擬合結果的影響。本文針對這些問題做了相關研究，定量分析了調和項對參數偏導數的影響數值，并給出了相關結論。

1 18參數廣播星歷用戶算法

18參數廣播星歷[3]是在原16參數廣播星歷[1，3]基礎上將長半軸、衛星運行平均角速度和升交點赤經的瞬時狀態參數重新定義，而其他參數定義不變所組合成的一組新的星歷。16參數廣播星歷用戶算法在相關研究中都給出了明確的算式[4-10]，而18參數廣播星歷用戶算法與16參數廣播星歷用戶算法的不同也正是由參數定義不同引起的，其具體算法如下：

1)

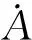
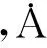
2)

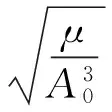
nA=n0+ΔnA.

3)

MK=M0+nA·tk；Ek=Mk+e·sinEk；

式中：MK是瞬時平近點角，Ek是瞬時偏近點角， Vk是瞬時真近點角。

4)

Φk=Vk+ω.

式中Φk為瞬時升交角距。

5)

δuk=cus·sin 2Φk+cuc·cos 2Φk；

δrk=crs·sin 2Φk+crc·cos 2Φk；

δik=cis·sin 2Φk+cic·cos 2Φk.

式中：δuk為升交角距的攝動改正量，δrk為衛星矢徑的攝動改正量，δik為軌道傾角的攝動改正量。

6)

uk=Φk+δuk；rk=Ak(1-e·cosEk)+δrk；

式中：uk為經過攝動改正的維度參數，rk為經過攝動改正的衛星矢量半徑，ik為經過攝動改正的軌道傾角。

7)

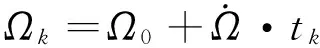
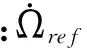
8)

xk=rk(cosukcosΩk-sinukcosiksinΩk)；

yk=rk(cosuksinΩk+sinukcosikcosΩk)；

zk=rksinuksinik.

2 基于其用戶算法的18參數廣播星歷偏導數推導

要擬合18參數廣播星歷，就必須建立參數與三維坐標之間的線性函數模型，通常采用泰勒公式將衛星位置函數進行線性化，僅取一階導數項[11]。那么求解每個參數的偏導數就成了擬合算法的關鍵步驟，同時偏導數求解的正確與否，將直接關系到擬合算法的正確性。

根據多元函數的求導方法，可以將衛星三維坐標函數對參數的偏導數表示為

(1)

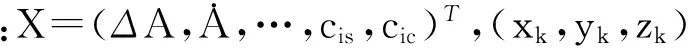
(2)

(3)

(4)

(5)

(6)

(7)

從它們的表達形式來看，都含有2(crscos2Φk-crcsin2Φk)、2(cuscos2Φk-cucsin2Φk)和2(ciscos2Φk-cicsin2Φk)系數項。根據廣播星歷參數的定義和取值范圍可知，crs，crc為102量級，cus，cuc為10-6量級，cis，cic為10-8量級，所以從定性的角度分析，調和項對以上6個參數的影響值很小，其具體的值可參考表1 。

表1 tk=14 400 s(4 h)時受調和項影響六參數的偏導數值統計

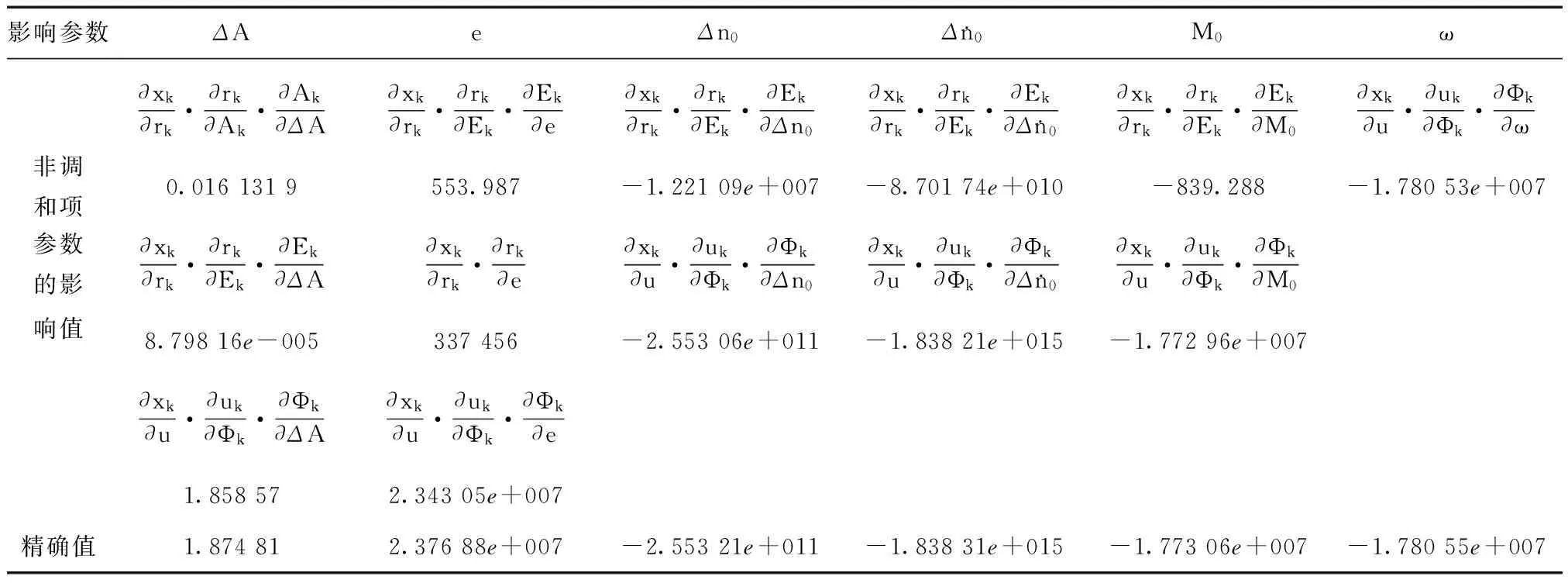
續表1

由于一般的擬合時長不超過4h，那么當選擇擬合時間段內的起始時刻為參考時刻時，同次迭代計算中tk≤14 400s，表1中各項偏導數的值基本可以代表同次迭代計算中的最大值。

從表1可以看出調和項對6個參數的影響較之精密偏導數值完全可以忽略不計，也就是說在推導參數偏導數時只需要考慮非調和項參數的影響，那么，將有

(8)

(9)

(10)

(11)

(12)

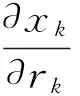
(13)

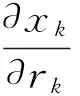
(14)

(-sinukcosΩk-cosukcosiksinΩk).

(15)

(16)

對于其余參數，偏導數與調和項系數無關，公式推導相對簡單，且無需忽略相關的中間變量，此處由于篇幅限制不做詳細說明，具體表達式可參考文獻[1]和文獻[2]。

3 計算和比較

根據以上所述原理，利用北斗12號MEO衛星2012-09-02采樣間隔為5min的定軌數據，擬合18參數廣播星歷，擬合時長分別為2h和4h，且選擇擬合時段的起始時刻為參考時刻，則toe在擬合過程中為已知值，那么實際需要擬合的只有17個參數。在實際的計算中，將分以下3種方案進行：

方案1：擬合算法采用精密偏導數，對參數進行擬合。

方案2：擬合算法采用僅僅忽略調和項的偏導數，對參數進行擬合。

方案3：擬合算法采用忽略調和項偏導數且同時采用簡化后的偏導數對參數進行擬合。

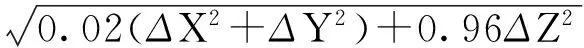
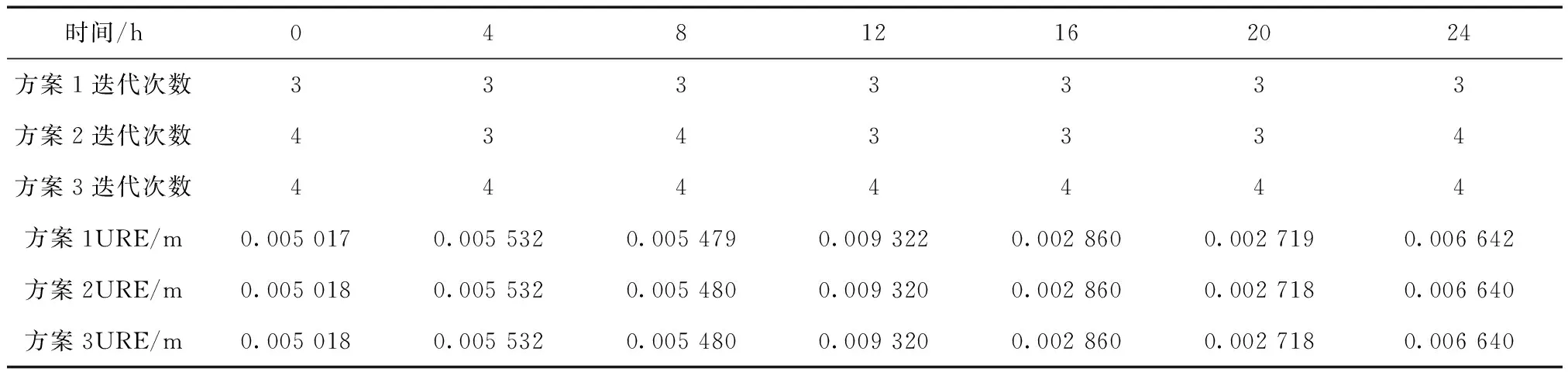
表2 擬合時長4 h時不同時刻參數擬合URE和迭代次數統計( |σ-σ0|<10-6)

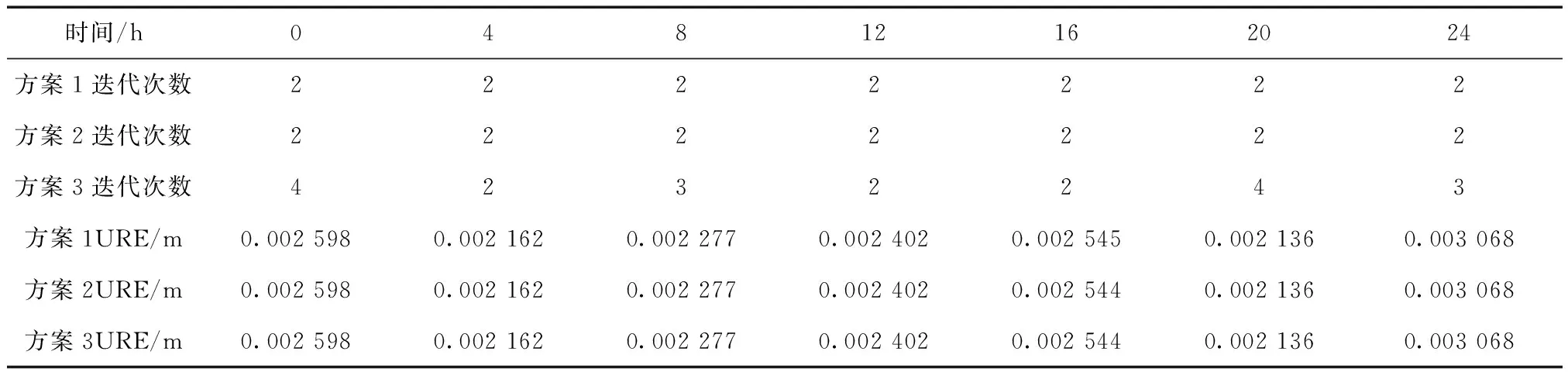
表3 擬合時長2 h時不同時刻參數擬合URE和迭代次數統計( |σ-σ0|<10-6)

表4 擬合時長4 h時不同時刻參數擬合URE和迭代次數統計( |σ-σ0|<10-9)

計算結果分析：

1)采用簡化的ΔA偏導數時，在同樣的迭代收斂條件下，擬合所需次數最多，而采用僅僅忽略調和項的偏導數時，迭代次數介于兩種算法之間，這說明ΔA偏導數的簡化使得參數擬合算法的迭代效率下降。

2)調整迭代終止條件擬合精度不會有太大的提升，然而縮短擬合時長卻能夠明顯提高擬合精度，這是因為迭代收斂的快慢與給定的參數初始值有很大的關系，當收斂條件為|σ-σ0|<10-3m時，其擬合精度已經很高了，當收斂條件再嚴時，給定同樣一組初始值，其收斂速度相同，再加上擬合所用數學模型的限制，擬合精度不會明顯增加。

3)從表2～4可以看出，3種方案的擬合精度基本相同，但是采用精密偏導數時迭代次數最少，迭代收斂最快。3種方案下參數的擬合精度差值在10-6量級，這相對于定位精度要求來說完全可以忽略不計， 可用方案3的參數偏導數代替精密偏導數。

4 結束語

利用地面觀測資料確定衛星的在軌位置，并通過相關算法快速精確地擬合出廣播星歷參數是衛星實時定位的關鍵步驟。本文根據最新定義的18參數廣播星歷模型在其用戶算法的基礎上推導了各參數的偏導數，并詳細分析了調和項對各參數的影響，通過實際數據測試，了解到考慮調和項導致算法變得復雜，計算效率降低，忽略調和項和簡化ΔA偏導數后算法相對簡單，計算效率高，且精度基本不會下降，因此，在實際運用時，宜采用簡化后的偏導數公式來提高衛星廣播星歷參數擬合算法的效率。

[1]崔先強，焦文海，賈小林，等.GPS廣播星歷參數擬合算法[J].測繪學院學報， 2004，21(4): 244-246.

[2]崔先強，焦文海，秦顯平.GPS廣播星歷參數擬合算法的探討[J].測繪科學，2006，31(1):25-26.

[3]崔先強，焦文海，賈小林，等.兩種GPS廣播星歷參數算法的比較[J].空間科學學報，2006，26(5):382-387.

[4]劉基余.GPS衛星導航定位原理與方法[M].2版.北京：科學出版社，2008.

[5]陳劉成，韓春好，陳金平.廣星歷擬合算法研究[J].測繪科學，2007，32(3)：19-25．

[6]許其鳳. GPS衛星導航與精密定位[M].2版.北京：解放軍出版社，2001.

[7]陳留成，唐波.參考系選擇對Kepler廣播星歷參數擬合精度的影響[J].飛行器測控學報，2006，25(4):19-25.

[8]郝金明.利用地面測軌資料擬合GPS廣播星歷[D].鄭州：解放軍測繪學院，1989.

[9]崔先強，唐穎哲，姬劍鋒，等.用基于Givens變換的QR分解計算類GPS廣播星歷參數[J].測繪工程，2006，15(4):5-8.

[10]GPS Interface Control Document (ICD-GPS-200E) [S].ARINC Research Corporation, June 2010:128-151.

[11]呂志偉，易維勇，曾志林.GPS廣播星歷算法及其分析[J].測繪科學技術學報，2010，27(2):83-85.

[責任編輯：劉文霞]

Analysisofharmonyterms’effectin18parametersbroadcastephemerisfittingalgorithmofBeidousatellite

WANG Le1, JIA Xiao-lin2，FAN Li-hong1，LI Li1，ZHANG Ai-neng1

(1. Chang’an University,Xi’an 710054, China; 2. Xi'an Research Institute of Surveying and Mapping, Xi’an 710054, China)

According to the newest 18 parameters broadcast ephemeris model defined by GPS ICD documents, every parameter’s partial derivative is derived in consideration of harmony terms or ignoring harmony terms. And the quantitative analysis is made on the simplification of partial derivative of ΔA.The Beidou MEO satellite orbit determination data is used to test the fitting algorithm neglecting the effect of the harmony terms and simplified partial derivative of ΔA.The result shows that neglecting the effect of the harmony terms to each parameter’s partial derivative and simplifying partial derivative of ΔAwill produce nearly no effect to the last fitting accuracy.

18 parameters broadcast ephemeris; harmony term; MEO; fitting algorithm

2013-04-18

地理信息工程國家重點實驗室開放研究基金資助項目(SKLGIE2013-M-2-1)

王 樂(1988-)，女，碩士研究生.

P228

：A

：1006-7949(2014)01-0039-06