一種反饋線性化彈道跟蹤制導律設計
張大元,雷虎民,王 君,肖增博,李慶良
(1.空軍工程大學 防空反導學院,西安 710051;2.93507部隊,石家莊 050200;3.95100部隊,廣州 510405)
為提高飛行器飛行性能,通常根據給定指標,利用優化算法對飛行軌跡進行優化以得到基準彈道和控制量[1-4],但優化使用的各種模型存在不確定性,這使得按照基準控制量控制無法實現理想軌跡。因此,需要設計軌跡跟蹤制導律,保證飛行器按理想軌跡飛行[5]。
軌跡優化和跟蹤一直是飛行器領域的研究熱點,如再入飛行器和無人機的軌跡優化和跟蹤,許多先進的控制律被應用于跟蹤制導律的設計中,取得了較好的跟蹤效果[5-9];文獻[10]采用幾何原理研究了一種非線性方案彈道跟蹤算法;Dukeman G A、Zhou W Y等人先后將線性二次型最優控制理論(linear quadratic regulator,LQR)應用于再入飛行器的軌跡跟蹤中[11-12],取得了較好的效果,但常用的跟蹤模型是基于小擾動線性化方法簡化的,適用范圍小且誤差隨使用區域擴大而增大,模型精確度較低,而反饋線性化方法是一種精確線性化方法[13],能夠提高模型線性化精度,從而提高跟蹤制導精度。因此,本文利用反饋線性化方法對導彈運動模型精確線性化,基于LQR理論設計彈道跟蹤制導律,最后對制導律進行了仿真。
1 反饋線性化理論
1.1 輸入-狀態線性化的定義和判定定理
反饋線性化的基本思想是通過狀態反饋消除動態系統的非線性部分,從而得到一個偽線性動態。其基本原理簡述如下[13]。
考慮非線性系統:
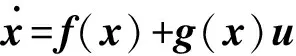
(1)
式中:x=(x1x2…xn)T∈D(D?Rn),f(x)、g(x)為定義在開集D上的Rn值映射,u為控制向量。映射f:D→Rn在微分幾何理論中被稱為D上定義的向量場,可表示為列向量:
f(x)=(f1(x)f2(x) …fn(x))T
(2)
設實值函數h:D→R和一個向量場f:D→Rn,h沿f的李導數定義為
(3)
對兩個向量場f:D→Rn、g:D→Rn,構造一個新的向量場,記為[f,g],定義式:
(4)
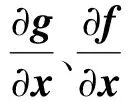
(5)
式中:k為李積的階數,k=0表示零階李積。下面給出一類非線性系統可輸入-狀態線性化的定義和判定定理。若式(1)所示的非線性系統可直接寫成:
(6)
式中:A為n×n陣,B為n×p陣,s(x):Rn→Rp和γ(x):Rn→Rp×p是定義在D上,且γ(x)對所有x∈D非奇異。
或是經過坐標變換z=T(x)使得式(1)所示系統在z下具有如下形式:
(7)
則稱式(1)所示非線性系統可通過坐標變換和狀態反饋線性化變成線性系統,方法是取控制量:
u=s(x)+γ(x)V
(8)
將式(8)代入式(7)得:
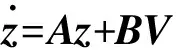
(9)
式中:V為反饋控制向量,可以使用各種線性控制系統設計方法設計。據文獻[13],式(1)所示非線性系統可反饋線性化的充要條件為引理1。
引理1式(1)所示非線性系統可輸入-狀態線性化的充要條件是:
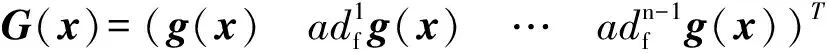
②下式所示的分布是對合的:
1.2 輸入-狀態線性化
對式(1)所示非線性系統,假設存在z=T(x),使得:
(10)
(11)
以上過程步步可逆,因此式(11)是z=T(x)滿足式(10)的充要條件。注意到z=T(x)不唯一,矩陣A、B可取為可控標準型(Brunovsky能控標準型),令:
z=T(x)=(T1(x)T2(x) …Tn(x))T
(12)
式中:Ti(x)為1×n維行向量,i=1,2,…,n,則式(11)可等價轉換為
(13)
由式(13)可求解轉換矩陣T(x)。
2 彈道跟蹤制導律設計
2.1 彈道跟蹤數學模型
導彈縱向平面質點運動模型如下所示:
(14)
式中:m,S為導彈質量和參考面積;v為導彈速度;Fp為發動機推力;θ為彈道傾角,單位為rad;q為動壓;g為重力加速度;Cx,Cy分別為阻力和升力系數。
在戰術導彈的設計過程中,首先會對速度特性進行設計,以確定發動機參數,因此,導彈速度可近似認為不可控,而導彈X坐標主要由速度決定,所以可去掉近似不受控的v和X變量,取彈道傾角θ和Y坐標作為系統狀態變量,同時考慮攻角為小量,得質點運動方程:
(15)
為實現基準優化彈道的跟蹤,化跟蹤問題為調節問題,取跟蹤變量的偏差量為狀態變量x,即:
(16)
對式(16)求導并將式(15)代入,得:
(17)
式中:不受控變量v和X取相應時刻基準彈道上的狀態值,用下標d標注。取攻角偏差量Δα為控制變量,用三角公式對式(17)化簡,可得到用于彈道跟蹤制導律設計的非線性模型:
(18)
2.2 制導律設計
下面利用反饋線性化理論將非線性模型(18)線性化,并利用LQR理論設計跟蹤制導律。
1)驗證可輸入-狀態反饋線性化條件。
由式(5)和式(18)知:
(19)
因此,
(20)
2)求解變換z=T(x)。
將式(18)代入式(13)得:
(21)
式中:z=T(x)=(T1(x)T2(x) …Tn(x))T。
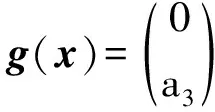
(22)
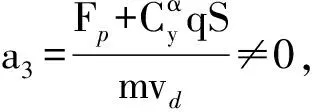
(23)
將式(23)代入式(21)第4式,得:
(24)
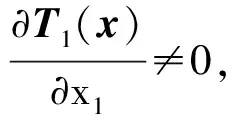
(25)
由式(25)知,T2(x)對f的李導數為
(26)
將式(25)、式(26)代入式(21)第3式,得:
(27)
將式(25)和式(27)代入式(8),得u的表達式為
(28)
則線性化后的系統為
(29)
3)利用LQR設計制導指令。
利用LQR對系統(29)進行設計,取二次型性能指標為
(30)
式中:Q、R為權重矩陣,且Q半正定,R正定。根據LQR理論,存在最優控制變量V=-Koptz,使得指標(30)最小,且最優反饋系數Kopt可按下式確定:
(31)
式中:P為黎卡提方程的解,O為零矩陣。
將式(25)、式(27)和式(31)代入式(28),可得彈道跟蹤制導指令計算公式為
(32)
式中:u0(t)為基準彈道控制量,x1=Y-Yd表示Y坐標測量值與基準值的偏差,x2=θ-θd表示彈道傾角測量值與基準值的偏差,Kopt1和Kopt2為最優反饋系數向量Kopt的分量。
至此,基于反饋線性化理論的彈道制導律設計完成。該跟蹤制導律工作流程如圖1所示。
圖1中,f(ΔY,Δθ,θd)=s(x)-γ(x)Koptz。制導工作流程為:首先,慣導和彈載機測量、計算導彈運動狀態,并與彈上存儲的基準彈道比較,得出偏差量;然后,根據導彈飛行時間從基準彈道數據庫中取出相應基準彈道參數,計算偏差控制量Δu和總控制量u*,控制導彈沿基準彈道飛行。
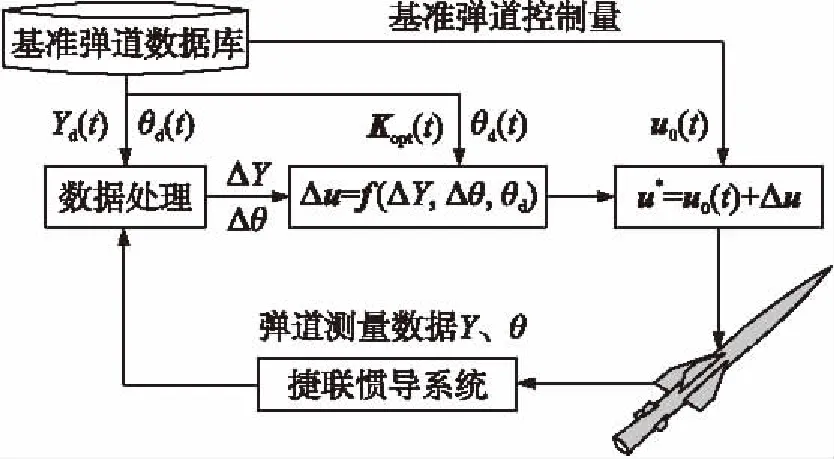
圖1 彈道跟蹤制導律工作流程圖
3 數字仿真
為驗證所設計的彈道跟蹤制導律的有效性,將其應用于導彈質點運動仿真。首先,給出隨機風干擾計算模型。由文獻[14]知,干擾力可等效為附加攻角,下面給出計算步驟。
3.1 隨機風干擾計算模型
①生成隨機地面風,根據風級定義,取地面垂直風速為3 m/s,即μ=0,σ=3 m/s,則:
(33)
式中:U0為地面垂直風,W0為地面水平風,NG為高斯白噪聲,μ、σ為均值和均方差。
②生成高空風速。
(34)
式中:U為高空垂直風,W為高空水平風,ρ0為地面處大氣密度,ρ為高空大氣密度。
③計算干擾攻角分量。
(35)
式中:Δα1為高空垂直風引起的干擾攻角,Δα2為高空水平風引起的干擾攻角,θ為彈道傾角。
④計算干擾總攻角。
Δα=Δα1+Δα2
(36)
等效干擾攻角計算結果如圖2所示。
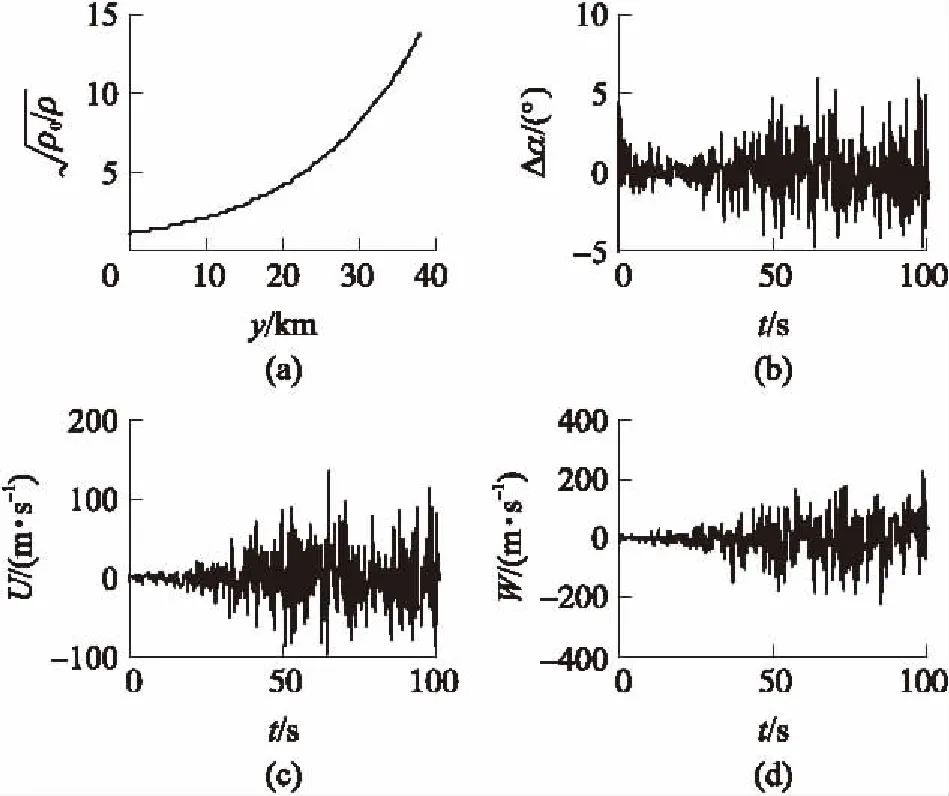
圖2 等效干擾攻角
3.2 彈道跟蹤制導規律仿真
為比較方便,根據文獻[14]直接給出導彈縱向平面運動小擾動線性化模型,如下所示:
(37)
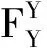
基于模型(37)和LQR控制理論同樣可設計LQR跟蹤制導律,命名為LQR制導律,本文設計制導律命名為反饋線性化+LQR制導律。
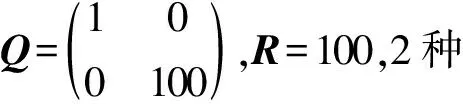
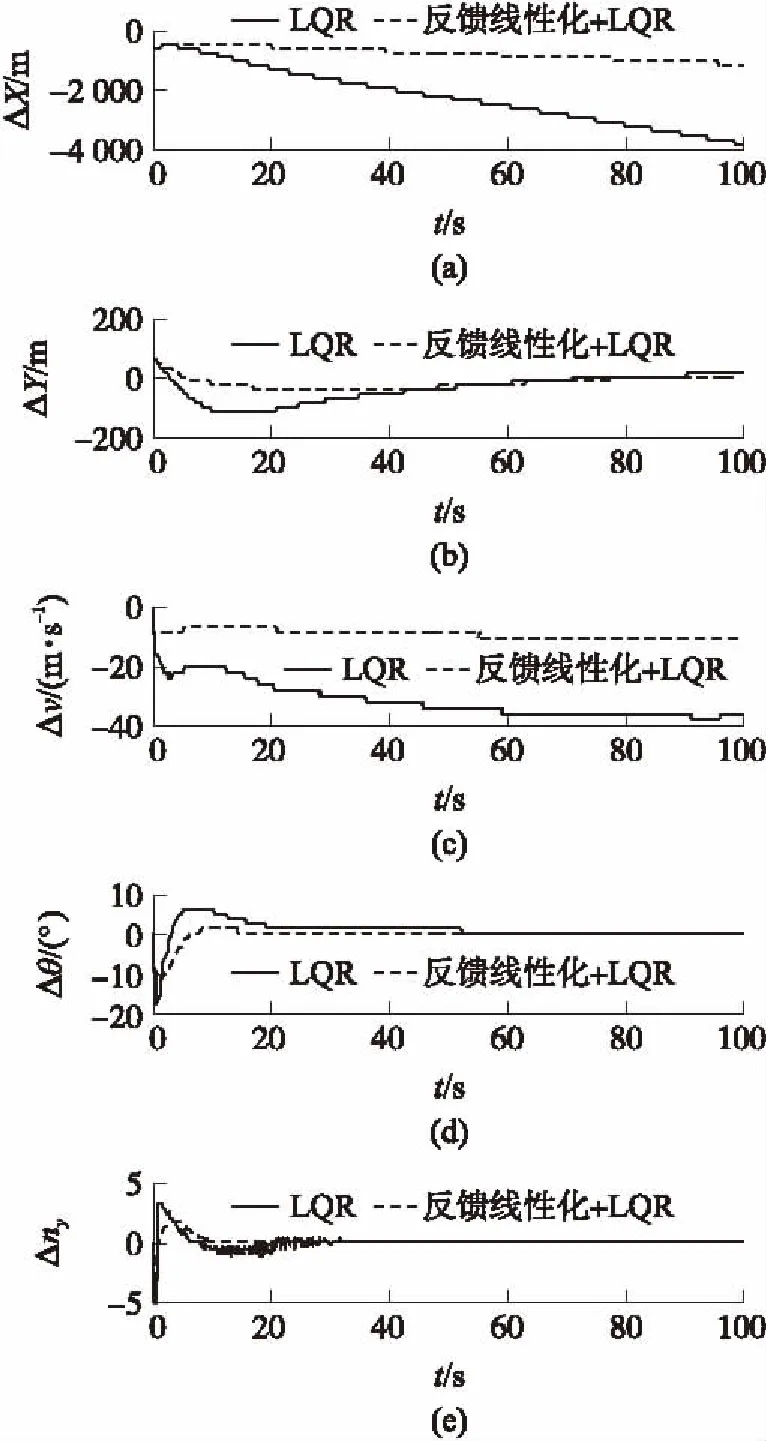
圖3 誤差和控制量曲線
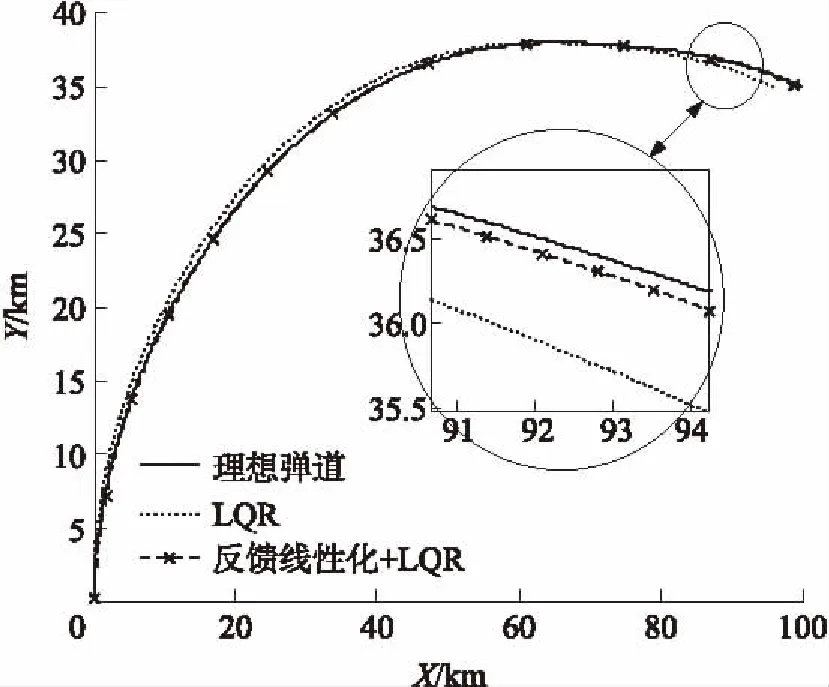
圖4 彈道曲線
仿真結果的數據統計見表1。表中數據表示誤差變化范圍。

表1 仿真結果統計
由圖3、圖4和表1可知:
①對受控的Y坐標和彈道傾角θ,跟蹤制導律能迅速消除初始誤差,并維持較小誤差水平,彈道跟蹤精度較高。
②對不受控的X坐標和速度v來說,反饋線性化+LQR的跟蹤誤差比LQR小,由表1數據知,ΔX絕對值的最大值從4 050.2 m減小到712.0 m,Δv絕對值最大值從38.3 m/s減小到10.0 m/s,大大減緩了不受控變量的發散速度。
③采用反饋線性化+LQR跟蹤制導律進行彈道跟蹤時所需的過載偏差控制量相對LQR較小,且抖振較小,易于工程實現。
綜上,在存在初始誤差和隨機風干擾的條件下,本文所設計的反饋線性化+LQR跟蹤制導律能較好抑制干擾作用,保證導彈穩定跟蹤基準彈道。
4 結束語
本文利用反饋線性化方法和LQR理論,設計了一種彈道跟蹤制導律。首先介紹了設計需用的輸入-狀態反饋線性化理論,然后對導彈運動非線性模型反饋線性化,并利用該精確線性化模型和LQR理論設計了一種跟蹤制導律。為比較所設計的跟蹤制導律,還利用傳統的小擾動線性化模型設計LQR跟蹤制導律,在存在初始狀態誤差和隨機風干擾條件下,將所設計的彈道跟蹤制導律和LQR制導律應用于導彈非線性運動仿真,結果表明,本文所設計的制導律由于使用反饋線性化精確模型,與使用小擾動模型的LQR制導律相比,能較好抑制初始偏差和隨機風干擾,保證導彈精確跟蹤基準彈道。本文的研究可推廣至三維彈道跟蹤制導律的設計中。
[1] LEVY M,SHIMA T,GUTMAN S.Linear quadratic integrated versus separated autopilot-guidance design[J].Journal of Guidance,Control,and Dynamics,2013,36(6):1 722-1 730.
[2] 楊希祥,張為華.基于Gauss偽譜法的空空導彈最優中制導律設計[J].國防科技大學學報,2013,35(1):28-32.
YANG Xi-xiang,ZHANG Wei-hua.Midcourse guidance law optimal design for air-to-air missiles based on Gauss pseudospectral method[J].Journal of National University of Defense Technology,2013,35(1):28-32.(in Chinese)
[3] 谷學強,王楠,陳璟,等.基于魯棒多目標優化方法的UCAV武器投放規劃[J].系統工程與電子技術,2013,35(4):753-760.
GU Xue-qiang,WANG Nan,CHEN Jing,et al.Weapon delivery planning for UCAV using robust multi-objective optimization approach[J].Systems Engineering and Electronics,2013,35(4):753-760.(in Chinese)
[4] 劉恒軍,姜歡,陳萬春.防空導彈動能殺傷多層彈道優化MDO算法應用[J].北京航空航天大學學報,2010,36(2):145-149.
LIU Heng-jun,JIANG Huan,CHEN Wan-chun.Application of MDO algorithm to multi-tier trajectory optimization design for a surface-to-air missile kinetic kill[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(2):145-149.(in Chinese)
[5] 湯善同,李忠應.變結構自適應制導規律研究[J].系統工程與電子技術,2002,24(7):68-76.
TANG Shan-tong,LI Zhong-ying.A guidance law of variable structure adaptive for missile following its optimal nominal trajectory[J].Systems Engineering and Electronics,2002,24(7):68-76.(in Chinese)
[6] BOUADI H,CAMINO F M.Aircraft trajectory tracking by nonlinear spatial inversion,AIAA 2012-4613[R].2012.
[7] PU Z Q,TAN X M,FAN G L,et al.Design of entry trajectory tracking law for a hypersonic vehicle via inversion control[C]//Proc of the 10th World Congress on Intelligent Control and Automation.Beijing:IEEE,2012:1 092-1 097.
[8] DROUOT A,RICHARD E,BOUTAYEB M.Nonlinear backstepping based trajectory tracking control of a gun launched micro aerial vehicle,AIAA 2012-4455[R].2012.
[9] 王俊波,曲鑫,任章.基于在線軌跡規劃的混合再入制導方法[J].宇航學報,2012,33(9):1 217-1 224.
WANG Jun-bo,QU Xin,REN Zhang.Hybrid reentry guidance based on the online trajectory planning[J].Journal of Astronautics,2012,33(9):1 217-1 224.(in Chinese)
[10] PARK S,DEYST J,HOW J P.A new nonlinear guidance logic for trajectory tracking,AIAA 2004-4900[R].2004.
[11] DUKEMAN G A.Profile-following entry guidance using linear quadratic regulator theory,AIAA 2002-4457[R].2002.
[12] ZHOU W Y,TAN S J,CHEN H B.A simple reentry trajectory generation and tracking scheme for common aero vehicle,AIAA 2012-4709[R].2012.
[13] 李殿璞.非線性控制系統[M].西安:西北工業大學出版社,2009.
LI Dian-pu.Nonlinear control system[M].Xi’an:Northwestern Polytechnical University Press,2009.(in Chinese)
[14] 李新國,方群.有翼導彈飛行動力學[M].西安:西北工業大學出版社,2005.
LI Xin-guo,FANG Qun.Flight dynamics of winged missile[M].Xi’an:Northwestern Polytechnical University Press,2005.(in Chinese)

