運動巧分解 “化難”細無聲
(江蘇省宜興第一中學,江蘇 宜興 214200)
一般曲線運動是高考試題中常見的一類難題,有關該類問題的求解策略較多,本文擬通過運用“運動的分解”這一常規(guī)思想來巧解帶電粒子在磁場中一般的曲線運動.
1 方法
帶電粒子在磁場中一般的曲線運動可分解成勻速直線運動和勻速圓周運動的合成.即把初速度分解為兩個方向,一個勻速直線運動,這個分速度大小必須滿足對應的洛倫茲力與所受的恒力的合力等值反向,另一個分速度則就是做勻速圓周運動的速度.此種方法適用于解決帶電粒子在復合場中一般的曲線運動,要求帶電粒子除洛倫茲力是變力外其它力必須是恒力.
2 應用
例1 在場強為B的水平勻強磁場中,一質量為m、帶正電q的小球在O點靜止釋放,小球的運動曲線如圖1所示.已知此曲線在最低點的曲率半徑為該點到x軸距離的2倍,重力加速度為g.求:
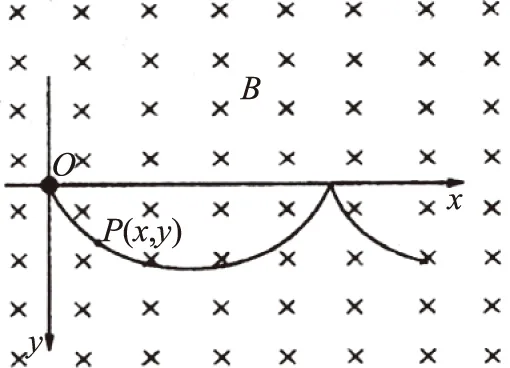
圖1
(1)小球運動到任意位置P(x,y)的速率v;
(2)小球在運動過程中第一次下降的最大距離ym;
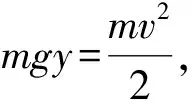
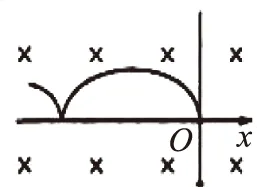
圖2
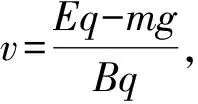
對于初速度不為零的復合場中的運動同樣適用,只是兩個方向上的速度不是等值反向,而是滿足兩速度的合速度即為初速度.
例2 如圖3所示,在豎直平面內,直線PQ右側足夠大的區(qū)域內存在豎直向上的勻強電場和垂直于紙面向里的勻強磁場,左側到直線距離為d1=0.4m的A處有一個發(fā)射槍.發(fā)射槍將質量m=0.01kg,帶電量q=+0.01C的小球以某一初速度v0水平射出,當豎直位移為d1/2時,小球進入電磁場區(qū)域,隨后恰能做勻速圓周運動,且圓周最低點C到直線PQ的距離為d2=0.8m.不計空氣阻力,g取10m/s2.試求:

圖3
(1)小球水平射出的初速度v0和電場強度E;
(2)小球從水平射出至運動到C點的時間t;
(3)若只將PQ右側的電場強度變?yōu)樵瓉淼囊话耄∏蜻M入電磁場區(qū)域后做曲線運動,軌跡的最低點為C′,求最低點C′離發(fā)射點A的豎直方向距離d及運動過程中的最小速度v.
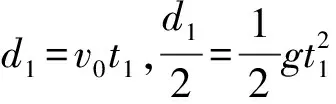
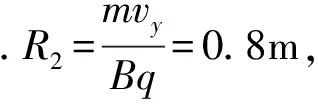
當小球運動至圓周運動的最高點時,速度與勻速向右的速度等值反向,所以它在運動過程中的最小速度為0.
由此可見這種方法不僅適用于初速度為零,同樣適用于以任何速度進入磁場中的運動,只要帶電粒子進入磁場后除洛倫茲力是變力外,其余力為恒力就可.速度分解的原則也簡單易掌握,即一個分速度所產生的洛倫茲力與所受恒力等值反向,另一個分速度則是做勻速圓周運動的速度.所以這種方法不失為解決帶電粒子在復合場中一般曲線運動的好方法.

