一類電力系統的分岔和奇異性分析

王曉東,陳予恕

(哈爾濱工業大學 航天學院，哈爾濱 150001)

電力系統振蕩是關系電力系統安全穩定運行的重要問題，除了正常運行的周期振蕩外，電力系統還時有發生混沌振蕩現象，其表現為非周期的、似乎無規則的、突發性或陣發性的機電振蕩，在振蕩嚴重的情況下會導致互聯系統的解列[1]。為此，越來越多的科學家和工程技術人員認識到電力系統穩定性問題的重要性，并將其作為系統安全運行的重要方面在理論和工程技術應用領域進行研究[2-6]。

對于單機無窮大系統，Duan等[7]分析了帶有一系列電容補償器的單機無窮大系統的次同步諧振，應用分岔理論分析了該系統出現的復雜的周期軌道分岔，環面折疊分岔；Zhu等[8]研究了單機無窮大系統中的次同步諧振，用Hopf分岔定理分析了Hopf分岔現象和穩定的周期解；Alberto等[9]應用Melnikov方法計算單機無窮大系統中異宿軌道橫截相交的條件；Wei等[10]研究了高斯白噪聲對電力系統安全盆侵蝕的影響； Chen等[11]用數值方法研究了單機無窮大系統中混沌現象并對其進行控制；Zhang等[12]分析了一個非線性三參數電力系統的異宿分支，用Melnikov函數確定了發生混沌現象的閾值，獲得了發生混沌現象的參數區域；Chen等[13]研究了一類電力系統的混沌和次諧振蕩，給出了Melnikov函數的計算方法，并獲得電力系統發生混沌振蕩和次諧振蕩的錐形參數區域；Nayfeh等[14]用多尺度方法分析了一種電力系統中的亞諧共振和混沌現象，并用數值方法得到了發生混沌現象的途徑；Abed等[15]采用的修正單機無窮大模型考慮了系統狀態對機組阻尼系數的影響，分析了Hopf分岔現象。

現有大多數文獻[10-14]中同步發電機采用的是常數阻尼，即令阻尼系數D為常數。實際上，阻尼在系統正常運行的情況下是與系統的狀態變量相關的，而且可能為正，也可能為負[15]。因此若D取用常值可能會改變系統的非線性動力學特性，不能真實反映系統的穩定性情況，影響了分析的準確性。

為此本文在文獻[15]提出的修正單機無窮大模型基礎上，建立了單機無窮大系統的數學模型，研究具有非線性阻尼時單機無窮大系統的動力學行為，運用多尺度法分析了周期負荷擾動下單機無窮大系統的主共振響應，求得了二階近似周期解的解析表達式，得到了主共振響應的幅頻曲線，應用C-L方法分析了不同參數區域內的局部分岔現象及其穩定性，通過數值仿真所得的結論，解釋了同步發電機在不同系統參數下對應的實際運行工況，也為同步發電機的穩定同步運行提供定性理論指導。

1 單機無窮大電力系統的數學模型

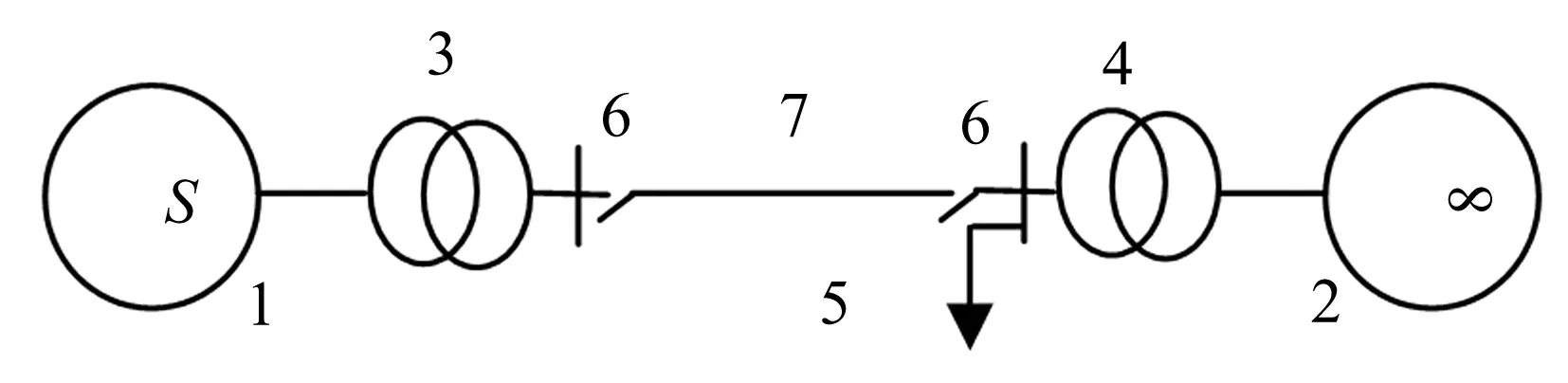
圖1 單機無窮大系統

單機無窮大系統模型如圖1所示。 圖1中“1”和“2”分別為同步發電機和無窮大系統，“3”和“4”為主變壓器，“5”為負荷，“6”為斷路器，“7”為系統聯絡線。設無限大母線電壓U∠0°為電壓參考相量，同步發電機的內電動勢為E，δ為發電機轉子q軸與同步參考軸間的相對角度，俗稱“功角”，ω為相對角速度，發電機的慣性時間常數為TJ，ω0為同步參考軸線的同步角速度，記M=TJ/ω0，發電機的機械輸入功率PM為恒定值，發電機到無限大母線之間的等效電抗為X，PE為發電機的電磁功率，則系統的數學模型為：

(1)

當發電機為隱極式時有：

考慮系統受到某周期性負荷擾動并考慮同步發電機的阻尼作用，則得：

(2)

式中:D為等值阻尼系數，PD為擾動功率幅值，Ω為擾動頻率。

做無量綱化處理，令:

并記:

則方程(2)化為：

(3)

為理解單機無窮大電力系統的動力學行為，首先對于無擾系統即c=0,f=0時的系統進行分析，可得其相圖如圖2所示：

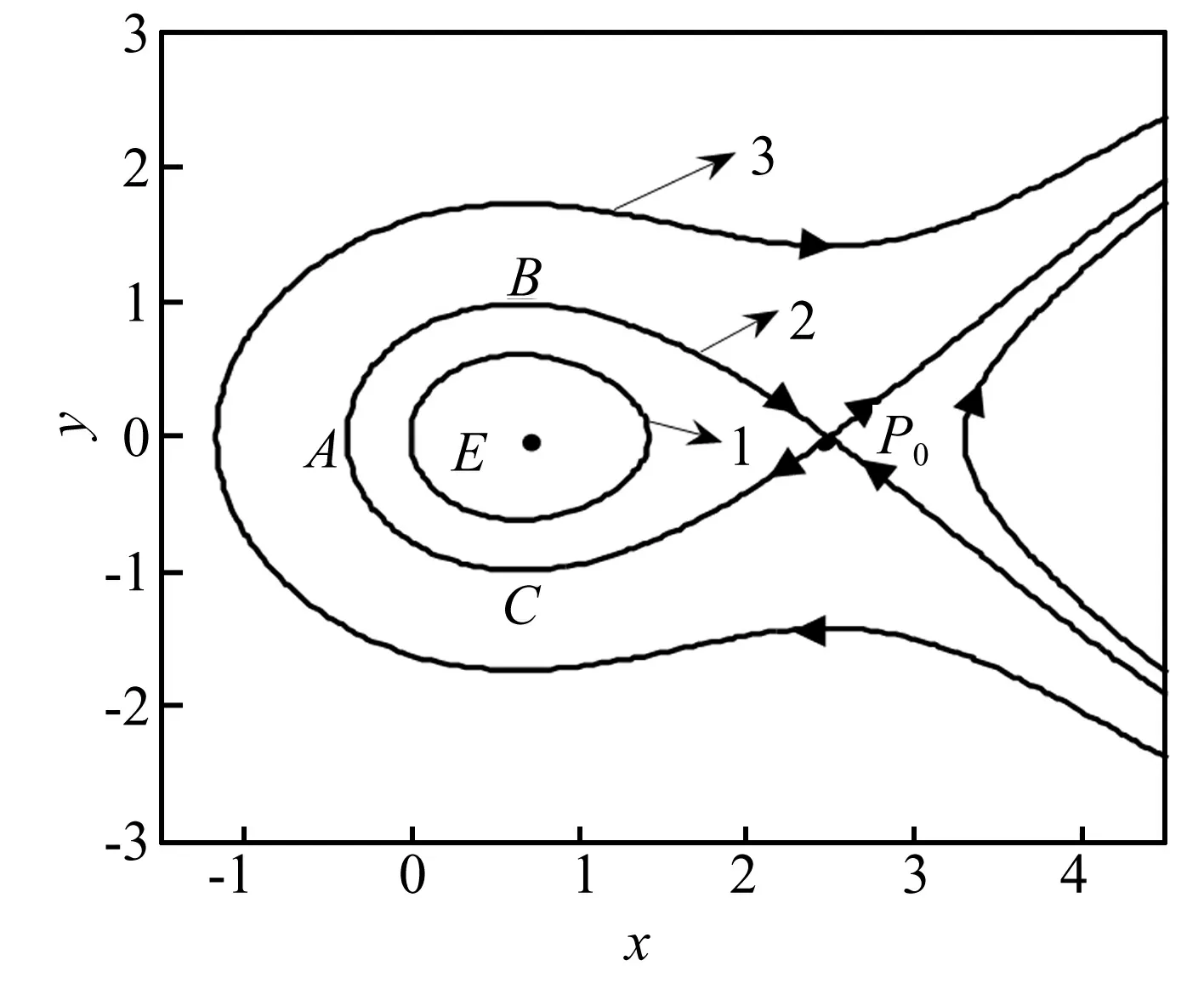
圖2 0<ρ<1時無擾系統的相圖

圖2是不同初始條件的無擾系統的相軌跡，“1”代表小幅振蕩軌道，“2”為聯接兩個平衡點的同宿軌道，為“1”與“3”的分界線，“3”代表旋轉軌道。

記無擾系統的平衡點為E,P0，則其坐標分別為：

(x1,0)=(arcsinρ,0), (x2,0)=(π-arcsinρ,0)

易知E(x1,0)為中心，P0(x2,0)為鞍點。

隨著參數ρ的增大，中心和鞍點的位置逐漸靠近，當參數ρ=1時，中心和鞍點重合在一起退化成為中心-鞍點(如圖3所示)，此時對應同步發電機穩定與不穩定的臨界點，系統處于靜態穩定極限，同時表明靜態穩定極限所對應的功角正好與最大電磁功率的功角一致。

圖3 ρ=1時，無擾系統相圖

考慮系統正常運行的情況下，同步發電機中阻尼與系統的狀態變量相關性作用，文獻[15]給出的修正單機無窮大模型考慮了系統狀態對機組阻尼系數的影響，結合文獻[16]給出的非線性阻尼模型(經驗公式)，本文用vander Pol阻尼代替常系數阻尼，即令式(3)中c=ξ+γx2，則得:

(4)

2 小幅振蕩的主共振分析

下面討論周期性負荷擾動時系統的主共振響應，將式(4)中的非線性項sinx在中心點(x1,0)=(arcsinρ,0)處Taylor展開，由奇異性理論[17]中的識別條件，保留至二次非線性項得：

(5)

重新標度方程令:

ξ→ε2ξ,γ→ε2γ,α→εα,f→ε2f, 0<ε?1為小參數，則方程化為：

(6)

現用多尺度法[18]尋求方程的漸近解：

x(t,ε)=x0(T0,T1,T2)+εx1(T0,T1,T2)+ε2x2(T0,T1,T2)

(7)

式中:T0=t,T1=εt,T2=ε2t，T0為快變時間尺度，T1,T2為慢變時間尺度。

研究主共振情況，因而設:

(8)

由多尺度法，比較ε同次冪的系數，得下列微分方程組：

(9)

(10)

(11)

方程(9)的復數形式的解為:

(12)

(13)

式中:cc表示等式右端函數的共軛復數部分，為使解中不出現久期項，須有:

D1A=0

由上式得：A=A(T2)，則方程(13)的特解為：

(14)

于是系統周期振蕩響應的二階近似解為:

將式(12),式(14)代入式(11)得：

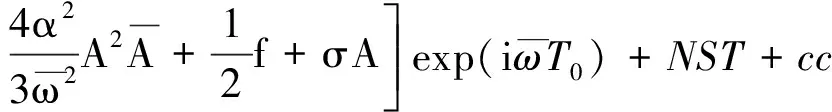
(15)

式中:NST表示不產生久期項的項，消除式(15)中的久期項得：

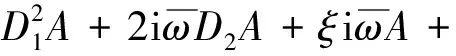
(16)

設:

(17)

式中:a,φ為T2的實函數，將式(17)代入式(16)分離實部與虛部得：

(18)

圖4 幅頻特性曲線

(19)

從方程組(19)消去φ得頻率響應方程：

(20)

討論定常運動的穩定性，設:

(21)

其中:a0,φ0為式(20)的一組解，a1,φ1為小的擾動量，將式(21)代入式(18)并對a1,φ1展開，注意到a0,φ0滿足式(19)并略去a1,φ1二階及以上微量，得：

(22)

因而定常運動的穩定性依賴于式(22)的右端的系數矩陣的特征值。

利用式(19)，可得特征方程為：

(23)

由特征方程的特征根可知，在幅頻曲線圖像(圖4)中，對于每一幅頻曲線，具有鉛垂切線的曲線之間的部分為不穩定，其余部分穩定，即當有多值解時，中間的一個解為不穩定的，其余兩個為穩定的，其在該區間內有可能發生振幅的跳躍現象。

圖5 響應幅值-激勵幅值曲線

3 主共振的奇異性分析

根據C-L方法[17]對方程(20)作奇異性分析，令:

z=a2

(24)

得:

c3z3+c2z2+c1z+c0=0

(25)

其中:

記:

c3(z3+ε2z2+λz+ε1)=c3G(z,λ,ε1,ε2)

G(z,λ,ε1,ε2)=z3+ε2z2+λz+ε1

(26)

取λ為分岔參數，ε1,ε2為開折參數，顯然G(z,λ,ε1,ε2)為芽g=(z,λ)=z3+λz的普適開折，且余維數為2。由奇異性理論[19]通過計算得：

圖6 轉遷集

圖7 不同保持域內的分岔圖

轉遷集如圖6所示，可以看出，轉遷集將平面ε1-ε2分成四個不同的保持域，在不同區域內的分岔模式如圖7所示，依之可調整系統參數達到選擇工程中允許的動態行為模式的目的，因而可為同步發電機不同運行參數和結構參數下的動力學分析、分岔控制和工程優化設計提供理論指導。

4 數值分析

為更好的理解單機無窮大電力系統隨著周期性負荷擾動的變化所呈現的動態特性，以下用數值仿真的方法討論系統(4)的動力學行為變化情況。

圖8 f不同時的分岔圖

由圖8可以看出，隨著激勵幅值f的增大，系統響應出現了倍周期分岔現象，軌道經歷了周期1→周期2→混沌解的變化。當激勵的幅值較小時，系統出現了周期1解，其相圖如圖9(a)所示，此時同步發電機可以保持同步運行，電力系統處于暫態穩定狀態，隨著外激勵幅值f增大，當f=0.72時出現了周期2解，其相圖如圖9(b)所示；當f=0.725 9時出現了混沌解，此時發電機功角出現了不規則也不衰減的類似隨機的混沌振蕩，功角不再穩定可靠，系統失穩。圖9(c)和圖9(d)分別為混沌狀態的相圖和對應的混沌吸引子，由全局分岔圖(圖8)可見，混沌狀態僅存在于擾動幅值f的一個很窄的數值范圍內，當f=0.79時出現了旋轉周期軌道，其相圖如圖9(e)所示，此時隨著功角δ的增大，加速轉矩不斷增大，使發電機轉子不斷加速，發電機就不可能再恢復到同步運行，系統由于增幅振蕩最終失去穩定，發電機失去同步后將在系統間產生功率和電壓的強烈振蕩，結果使發電機組和負荷被迫切除，甚至導致系統解列或瓦解。

圖9 f不同時的相圖及混沌吸引子

5 結 論

本文應用非線性動力學的解析方法，分析了在周期性負荷擾動下電力系統振蕩的失穩現象，考慮了同步發電機非線性阻尼轉矩的作用，比傳統文獻更貼近工程實際，由于保留了電力系統的非線性特征，因此所得結果能夠更好地反應振蕩失穩的機理，可以為電力系統的穩定運行提供依據，具體有：

(1)應用多尺度方法和C-L方法，對受周期負荷擾動的單機無窮大電力系統的主共振進行了研究，得到了系統小幅振蕩周期解的二次解析表達式和幅頻響應方程，分析了定常解的穩定性并得到了系統穩態響應分岔方程的轉遷集和對應的分岔圖，研究表明該系統的不同分岔模式與其運行參數和結構參數有密切聯系，可為同步發電機的動力學分析、分岔控制和工程優化設計提供理論指導。

(2)電力系統在周期性激勵下，當擾動激勵幅值較小時，同步發電機功角具有小幅振蕩周期解，數值結果與理論結果一致，同步發電機能夠保持同步運行，擾動幅值達到某個臨界值時，發電機功角出現不規則的振蕩現象，系統處于混沌振蕩狀態，影響了系統的正常運行，同步發電機失步，電力系統失穩，擾動幅值若繼續增大，發電機功角持續增大，同步發電機失步，造成系統解列。

參 考 文 獻

[1]盧 強，梅生偉，孫元章.電力系統非線性控制[M].北京：科學出版社，1993.

[2]賈宏杰，余貽鑫，王成山.電力系統混沌現象及相關研究[J].中國電機工程學報，2001，21(7)：26-30.

JIA Hong-jie，YU Yi-xin，WANG Cheng-shan.Chaotic phenomena in power systems and its studies[J].Proceedings of the CSEE，2001,21(7):26-30.

[3]Gerardo E P,Paul M O,Arnau D C,et al.Output-feedback IDA stabilisation of an SMIB system using a TCSC[J].International Journal of Control,2010,83(12): 2471-2482.

[4]Shi J,Tang Y,Dai T,et al.Determination of SMES capacity to enhance the dynamic stability of power system[J].Physica C,2010,470 (20):1707-1710.

[5]Manjarekar N S,Banavar R N,Ortega R.Application of interconnection and damping assignment to the stabilization of a synchronous generator with a controllable series capacitor[J].International Journal of Electrical Power and Energy Systems,2010,32(1): 63-70.

[6]Kumaran R C,Venkatesh T G,Swaru K S.Voltage stability-Case study of saddle node bifurcation with stochastic load dynamics[J].International Journal of Electrical Power & Energy Systems,2011,33(8): 1384-1388.

[7]Duan X Z,Wen J Y,Cheng S J.Bifurcation analysis for an SMIB power system with series capacitor compensation associated with sub-synchronous resonance[J].Science in China.Series E: Technological Sciences,2009,52(2): 436-441.

[8]Zhu W,Mohler R R.Hopf bifurcations in a SMIB power system with SSR[J].IEEE Transactions on Power Systems,1996,11(3): 1579-1584.

[9]Alberto L F C,Bretas N G.Application of Melnikovs method for computing heteroclinic orbits in a classical SMIB power system model[J].IEEE Transactions on Automatic Control,2000,47(7): 1085-1089.

[10]Wei D Q,Zhang B,Qiu D Y,et al.Effect of noise on erosion of safe basin in power system[J].Nonlinear Dynamics,2010,61: 477-482.

[11]Chen H K,Lin T N,Chen J H.Dynamic analysis,controlling chaos and chaotification of a SMIB power system[J].Chaos,Solitons and Fractals,2005,24: 1307-1315.

[12]Zhang W N,Zhang W D.Chaotic Ocillation of a Nonlinear Power System[J].Applied Mathematics and Mechanics,1999,20(10): 1175-1183.

[13]Chen X W,Zhang W N,Zhang W D.Chaotic and subharmonic oscillations of a nonlinear power system[J].IEEE Transactions on Circuits and Systems Ⅱ ,2005,52(12): 811-815.

[14]Nayfeh M A,Hamdan A M A,Nayfeh A H.Chaos and stability in a power system: subharmonic-resonant case[J].Nonlinear Dynamics,1991,2: 53-72.

[15]Abed E H,Varalya P P.Nonlinear Oscillations in Power systems[J].International Journal of Electrical Power & Energy Systems,1984,6(1): 37-43.

[16]Liwschitz M M.Positive and negative damping in synchronous machines[J],AIEE Trans,1941,60: 210-213.

[17]陳予恕.非線性振動系統的分岔和混沌理論[M].北京：高等教育出版社，1993.

[18]陳予恕.非線性振動[M].北京：高等教育出版社，2002.