振動壓路機振動壓實附著性能研究

劉占獻,孟凡皓,李 雨,張曉波

(長安大學道路施工技術與裝備教育部重點實驗室，陜西西安 710064)

振動壓路機振動壓實附著性能研究

劉占獻,孟凡皓,李 雨,張曉波

(長安大學道路施工技術與裝備教育部重點實驗室，陜西西安 710064)

對單鋼輪振動壓路機在振動壓實時前輪附著力變化的原因進行分析，并據此設計相應的試驗。試驗結果表明，低頻高幅振動時總牽引力明顯減小，且在1擋和3擋工況時鋼輪出現打滑現象。提出振動壓實時前輪有效附著系數的概念，并給出計算公式，根據試驗數據計算出在振動壓實時有效附著系數約為靜壓時的46%，并且通過理論分析得出在2擋時附著系數利用率最高。可為振動壓路機參數設計和工程應用提供一定的參考和依據。

附著性能;有效附著系數;振動壓實;牽引力

驅動能力是單鋼輪振動壓路機的一項非常重要的性能指標，該能力與發動機和傳動系統的工作參數有關，壓路機的附著性能影響驅動能力的發揮[1]。所以研究振動壓路機的附著性能對于提高其加速性能、爬坡能力、作業質量具有重要意義。

設計和評價振動壓路機牽引性能時，通常都是只考慮液壓系統最大驅動性能或采用鋼輪單行走時的測試結果，沒有采用振動壓實時牽引性能的測試結果。而單鋼輪壓路機工作時，鋼輪是振動狀態，其正壓力是一個呈正弦交變的負荷，有效附著系數與平穩行走時差異巨大，所以只根據平穩行走時的牽引性能來設計壓路機有一定的不足。平穩工作時有效驅動性能的發揮，對壓路機作業質量和機器作業性能影響巨大。因此研究作業時的有效附著特性對壓路機驅動系統設計和整機性能發揮意義重大。

1 振動壓實的附著力

為了保證作業質量，壓路機最大驅動能力往往受液壓系統驅動能力限制。當驅動力大于材料附著極限能夠提供的有效摩擦力時，會導致材料推移，影響壓實質量。所以最大驅動力應該小于或等于材料附著系數極限所提供的最大摩擦力。壓路機可能達到的最大牽引力由液壓系統的輸出特性決定，但驅動輪能否產生驅動力或產生多大的驅動力則取決于驅動輪的附著力Pφ，靜壓時的表達式[2]為

Pφ=φGφ，

(1)

式中φ為附著系數，取決于地面的性質和驅動輪的結構特征及其之間的作用；Gφ為驅動輪分配質量，取決于整機的質量和重心的幾何位置。

由于牽引力受附著極限的限制，且低頻高幅時的牽引力相對于靜壓時明顯減小，振動使附著極限減小，從而使牽引力減小。由式(1)可知， 振動通過影響附著系數φ和驅動輪實際分配質量Gφ來影響附著極限。

1.1振動壓實對鋼輪附著系數Gφ的影響

根據振動壓實理論，當激振頻率與振壓材料的固有頻率一致時，振壓材料的內摩擦力最小，壓實效果最好[3]。為了提高作業效率，壓路機的設計振動頻率很接近土體的二階固有頻率25 Hz[4]，振動頻率一般設置在26～33 Hz，即壓路機在振動壓實時土體一般很接近共振狀態。當低頻高幅振動時，振動頻率為26.9 Hz，振壓土體最接近共振狀態，此時與鋼輪接觸的土的表面最容易被破壞，使得附著性能減小。

1.2振動壓實對振壓作用力的影響

在振動壓實的過程中，壓路機對土體的實際振壓作用力Fs是動態振壓力F與鋼輪分配重力Gφ之和，即Fs=F+Gφ[5]。

根據壓路機—土壤動力學模型，動態振壓力F的表達式為

F=(k2-msω2+ic2ω)x2,

式中ω為激振頻率；x2為鋼輪振幅；ms、k2、c2分別為土體隨動質量、剛度和阻尼。

則有

Fs=(k2-msω2+ic2ω)x2+Gφ.

壓路機—土壤動力學模型[6]是線性時變系統，激勵是諧振力，所以穩態響應也是諧振位移，即鋼輪振幅x2為正弦曲線，因此實際振壓作用力Fs是繞其平衡位置波動的正弦曲線[7]。

在振動壓實的過程中，由于鋼輪對土體的作用力不是靜力，所以不能用式(1)計算附著力。

2 附著性能的試驗研究

根據以上分析可知，在振動壓實時不僅附著系數會產生變化，而且鋼輪與土壤間的作用力也會產生較大變化。因此，需要通過試驗進一步研究。

首先在靜壓條件下測試振動壓路機的牽引性能，分別測出在1擋、2擋、3擋、4擋(均為前進擋)時壓路機的最大牽引力；然后在振動條件下測試振動壓路機的牽引性能，分別測出在1擋、2擋、3擋、4擋(均為前進擋)時壓路機低頻高幅和高頻低幅時的最大牽引力，測試結果如表1所示。

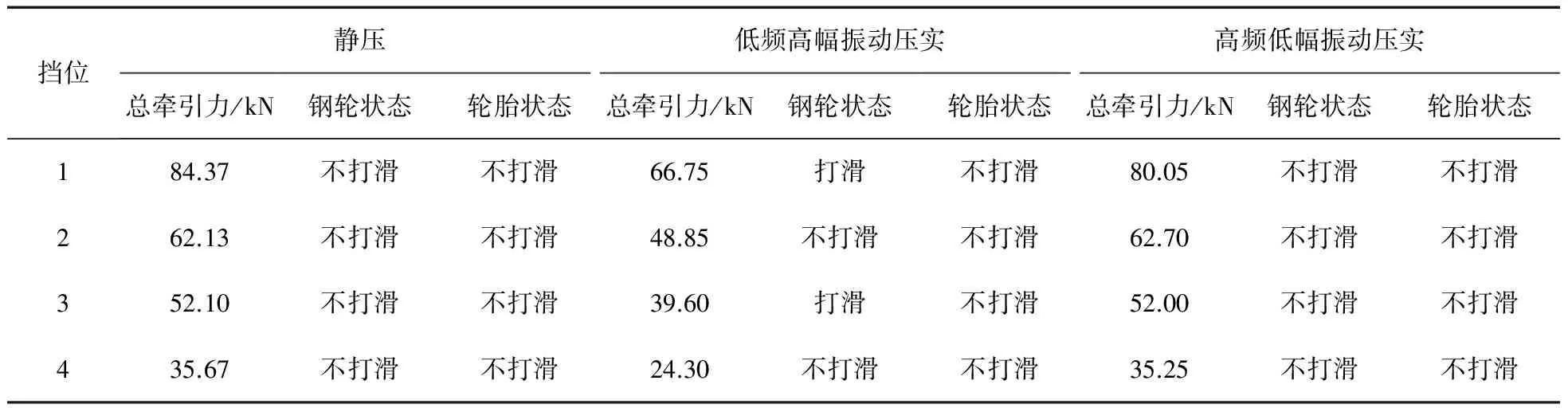
表1 靜壓和振動壓實時各擋位總牽引力與驅動輪狀態

由表1可知，靜壓時的牽引力和振動時的牽引力均隨著擋位的增加而逐漸減小;同一擋位高頻低幅時的牽引力和靜壓時的牽引力大致相等;同一擋位低頻高幅振動時的牽引力相對靜壓時的牽引力明顯減小；只有在低頻高幅振動壓實時1擋、3擋鋼輪出現打滑現象。

3 鋼輪有效附著系數計算方法

3.1靜力作用下鋼輪打滑工況的判定

當壓路機在靜壓條件下進行牽引力測試時，輪胎的附著力Pφ1和鋼輪的附著力Pφ2分別為

Pφ1=Gφ1·φ1=41.8 kN,Pφ2=Gφ2·φ2=51.68 kN，

其中Gφ1、Gφ2分別為輪胎和鋼輪的分配質量；φ1、φ2分別為土體對輪胎和鋼輪的附著系數。

壓路機振動輪牽引力分配系數Cm為

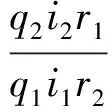
式中q1、i1、r1分別為后輪馬達的排量、總傳動比、動力半徑；q2、i2、r2分別為前輪馬達的排量、總傳動比、動力半徑。

為了確定哪一個驅動輪先打滑，有判別式[1]

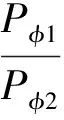
1)當A<1時，后輪先打滑；2)當A>1時，前輪先打滑；3)當A=1時，壓路機能夠最大限度地利用前后輪的附著能力。

根據液壓系統的參數，計算出各擋位判別式，如表2所示。

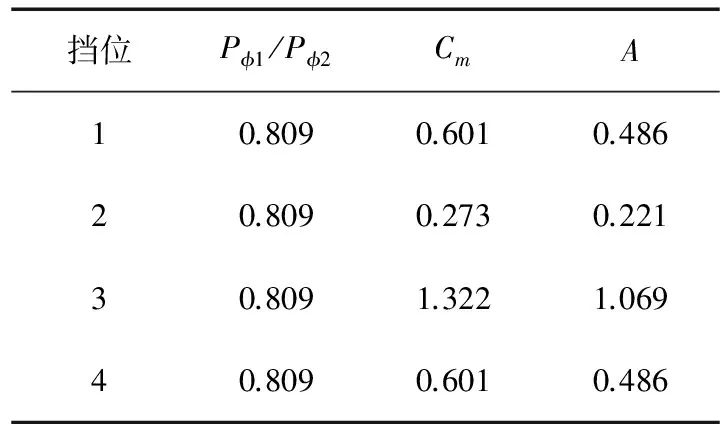
表2 各擋位的判別式

由表2可知，靜壓時如果打滑，1擋、2擋、4擋只可能后輪打滑，而3擋只可能前輪打滑。但是試驗中在振動情況下前輪的附著系數會減小，使得Pφ2減小，最終使A增大，即1擋和4擋時A>1，使得工況發生變化，導致前輪打滑；由于2擋時A非常小，即使Pφ2減小A也不會大于1，即振動時2擋的前輪不會打滑。

圖1～ 4為振動情況下測得的總牽引力和行走馬達的轉速。

由圖1、3可以得出，振動壓實過程中1擋、3擋明顯打滑，并能保持穩定，說明此種情況下鋼輪附著系數的減小使1擋時A變大了，并且>1；而由圖2、4可知，鋼輪沒有打滑，這說明鋼輪附著系數的減小雖然使2擋時A變大了，但仍然<1，4擋沒有打滑是因為牽引力較小，沒有達到附著極限。

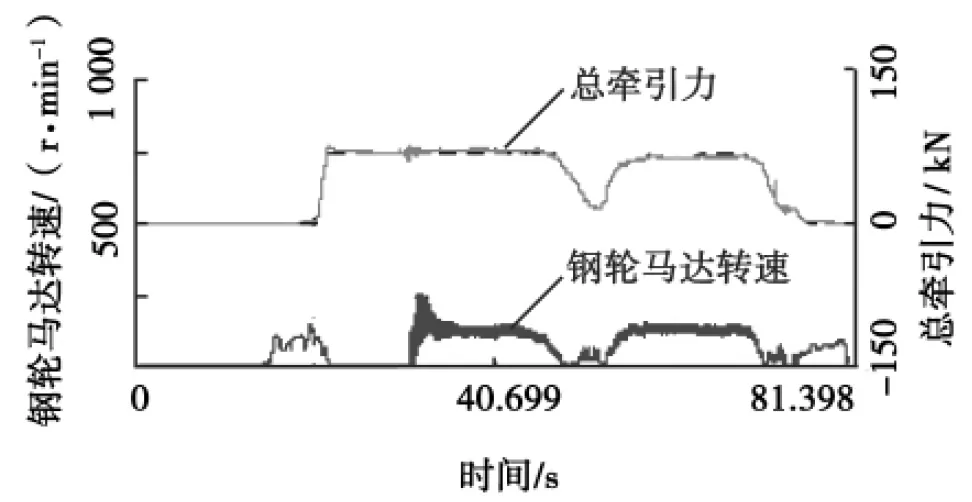
圖1 1擋總牽引力和鋼輪馬達轉速

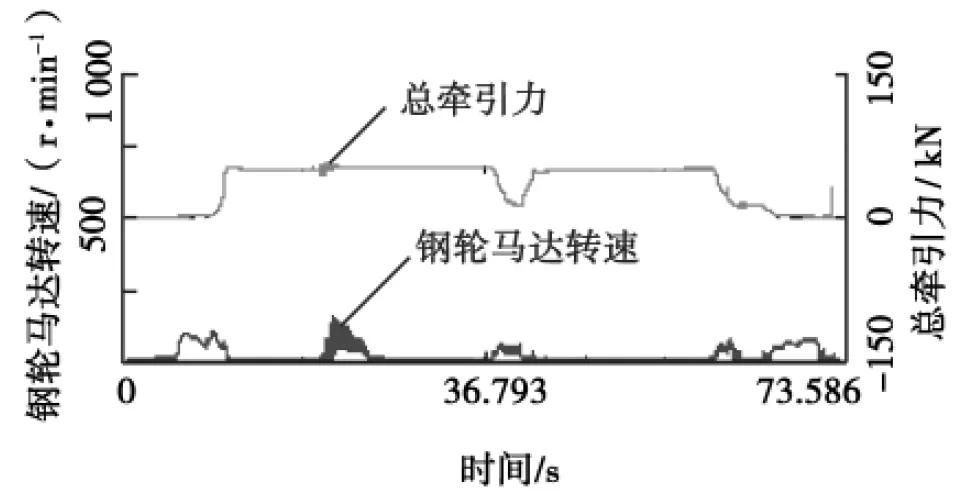
圖2 2擋總牽引力和鋼輪馬達轉速

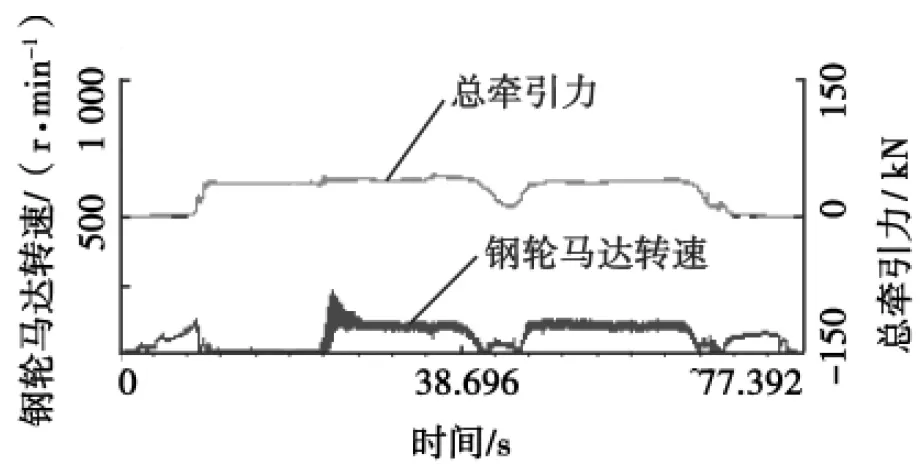
圖3 3擋總牽引力和鋼輪馬達轉速

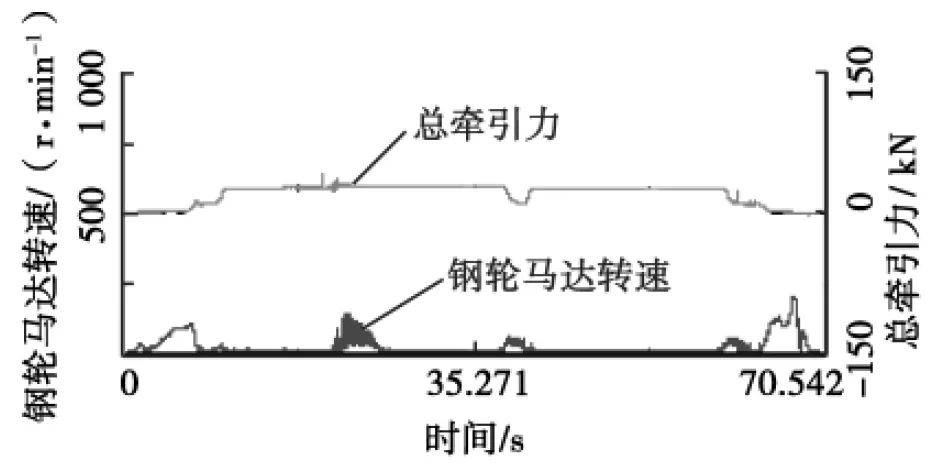
圖3 3擋總牽引力和鋼輪馬達轉速

3.2有效附著系數的計算

由于在振動壓實過程中的附著系數和鋼輪對土體的作用力均發生了變化，在工程應用中如果用2個變量計算振動過程中的附著力顯然比較麻煩，為了簡化計算過程，在此提出一種新的計算方法，即根據控制變量法的原理，在振動過程中將鋼輪對土體的作用力仍看作前輪分配質量，將附著力的減小都歸因于附著系數的減小，此時的附著系數稱之為有效附著系數，記為φ0。

由于低頻高幅振動時只有1擋、3擋鋼輪打滑，即鋼輪的牽引力超過了附著極限。此種工況下可以通過振動輪牽引力分配系數Cm計算出鋼輪的牽引力PK2。 后輪的牽引力PK1的表達式(不考慮液壓系統的傳動效率)為

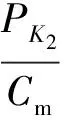
此時總牽引力為

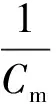
有效附著系數的表達式為

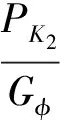
(2)

根據式 (2) 計算出低頻高幅振動時1擋、3擋有效附著系數，如表3所示。其中i1=67、i2=46、r1=0.7、r2=0.8、Gφ=129.2 kN。

表3 1擋、3擋有效附著系數

由表3可以看出，有效附著系數的平均值大約為0.184，可以看成定值，不隨擋位和牽引力的變化而變化，表征的是附著極限性能。在靜壓時附著系數一般取0.4，而在振動的情況下有效的附著系數降低到0.184，相對于靜壓時附著系數減小了54%左右。

4 結語

全液壓單鋼輪振動壓路機的動力性能是一項非常重要的指標，而動力性能的發揮取決于附著性能。本文主要對壓路機振動壓實時的附著特性進行了研究。為了便于工程分析和計算，根據控制變量法的原理，提出了單鋼輪振動壓路機前輪有效附著系數的概念，并給出其計算公式。由計算結果可以看出，振動壓實時有效附著系數明顯減小，只有靜壓時的46%左右。同時，從各擋位判別式的值可以看出， 2擋振動壓實時鋼輪不易打滑，附著系數利用率最高。

[1]尹繼瑤.全液壓振動壓路機行駛的動力性能與防滑轉[J].建設機械技術與管理,2010(1):99-102.

[2]孫江生，張維良，周殿春.輪式車輛地面附著系數的表達式分析[J].水利電力機械，2002,24(4):46-47.

[3]張光裕.工程機械底盤構造與設計[M].北京：中國建筑工業出版社，1980:132-136.

[4]湯振周.振動壓路機技術參數對壓實效果的影響分析[J].機電技術，2007，30(1):30-31.

[5]萬世宏.振動壓實系統的動力學理論分析[J].武漢工學院學報,1987，9(1):102-112.

[6]鄭書河，林述溫.智能振動壓路機動力學特性建模分析[J].中國工程機械學報，2011,9(4):398-403.

[7]楊士敏，傅香如.工程機械地面力學與作業理論[M].北京：人民交通出版社，2010:179-180.

(責任編輯：郭守真)

StudyonAdhesionPropertyofVibratoryRollerinProcessofVibratoryCompaction

LIUZhan-xian,MENGFan-hao,LIYu,ZHANGXiao-bo

(KeyLaboratoryforHighwayConstructionTechnologyandEquipmentofMinistryofEducation,Chang′anUniversity,Xi′an710064 ,China)

In order to be convenient for engineering calculations,the relative experiment is designed after analyzing the reasons why the adhesion force on the front wheel of the single vibratory road roller changes in the process of vibratory compaction. According to the result of the experiment, there is a significant decrease in the total traction force when the frequency is relatively low and the amplitude is relatively high and there exists a slipping phenomenon in the first gear and third gear. And then, a concept of effective adhesion coefficient is put forward and its calculation method is provided. The effective adhesion coefficient calculated by experimental data in the process of vibration compaction is about 46 percent of the adhesion coefficient in the process of static compaction. Finally, a conclusion is drawn that the utilization rate of adhesion coefficient is highest in the second gear. It is hoped to provide some reference and basis for the parameter design of vibratory roller and engineering applications.

adhesion property; effective adhesion coefficient; vibration compaction; traction

2013-12-26

劉占獻(1988—)男,河南駐馬店人,長安大學碩士研究生，主要研究方向為機械設計及理論.

10.3969/j.issn.1672-0032.2014.01.018

U415.52

A

1672-0032(2014)01-0082-05