Estimating runoff coefficient for quantity assessment of roof rainwater harvesting system

Zhang Wei Li Simin Tang Fengbing

(School of Urban Construction, Hebei University of Engineering, Handan 056038, China)

?

Estimating runoff coefficient for quantity assessment of roof rainwater harvesting system

Zhang Wei Li Simin Tang Fengbing

(School of Urban Construction, Hebei University of Engineering, Handan 056038, China)

In order to accurately estimate the runoff coefficient for the quantity assessment of the roof rainwater harvesting system(RRHS), great differences in the value of event runoff coefficient (ψERC) were observed by field monitoring under different roof types (roof slope and material) and diverse rainfall distributions (rainfall depth and intensity) in three years (2010 to 2012) in Handan, Hebei, China. The results indicate that the distribution ofψERCis more highly correlated with the event rainfall depth than other factors. The relationship betweenψERCand the rainfall depth can be well represented by the piecewise linear function. Further, based on the daily rainfall data over the period from 1960 to 2008, the value of the annual runoff coefficient (ψARC) is calculated. Although the total rainfall depth in each year is different,ψARCin Handan can be considered as a constant (0.62) approximately. The results can be used for the quantity assessment and performance analysis of the RRHS.

roof rainwater harvesting system; event runoff coefficient; annual runoff coefficient; rainfall depth

In recent years, roof rainwater harvesting systems (RRHS) have been widely applied as an alternative way to cope with the worsening urban water crisis in many countries. Taking into consideration the uneven spatial and temporal distribution of natural rainfall, many studies focused on the optimum methods of rainwater tank design for improving the cost effectiveness of the RRHS[1-3]. Whatever method was used, available runoff depth (or volume) was an indispensable parameter. Some researchers identified available runoff depth from roof catchments with rainfall depth approximately because roof catchments were the impervious surface[4-5]. However, there were hydrological losses of rainfall runoff caused by evaporation and minor infiltration in roof catchments[6]. For this reason, the runoff coefficient was introduced to calculate the value of available runoff depth on either an event or an annual basis[7].

The event runoff coefficient (ERC) is regarded as the ratio of runoff depth to rainfall depth, which reflects the influence of rainfall types on available runoff depth in different rainfall events. The value of ERC (ψERC) was usually selected as one constant but might not be the same numeric value in previous literature[8-11]. Actually,ψERCvaries greatly, influenced by catchments characteristics and rainfall distributions[12]. The results on the impact of roofing types and materials on ERC indicated thatψERCon sloping concrete/asphalt roofs, sloping metal roofs and flat gravel roofs were 0.9, 0.95 and 0.8 to 0.85, respectively[13]. Furthermore, little information was available onψERCunder different rainfall conditions. The annual runoff coefficient (ARC) was determined using the ratio of total runoff to total precipitation based on the annual rainfall data, which was adopted to assess the rainwater harvesting potential[14]. Catchment characteristics were the decisive factors for the value of ARC (ψARC) in the developing watersheds of Orlando, Florida[15]. By contrast, the work in Sicilian basins indicated that average annual rainfall depth and average annual temperature were the main climate parameters ofψARC[16].

The purpose of this study focuses on analyzing the influence factors ofψERCon roof catchments and developing a simple empirical method for estimatingψERC. Besides,ψARCbased on daily rainfall data is also discussed.

1 Materials and Methods

1.1 Study sites

Four different roof catchments are selected in Handan city, which is located in the south portion of Hebei province, China. In the study region, the mean annual rainfall and temperature are 558.5 mm and 13.5 ℃, respectively. The main characteristics of selected roofs are shown in Tab.1. The roof materials include asphalt, concrete and tile and the slopes are from 2.5% to 100%, where the selected roof types are commonly used in Handan. BecauseψERCis little correlated with the catchments area[8], the influence of the area is ignored in this study.

1.2 Data collection

Tab．1 Main characteristics of selected roof catchments

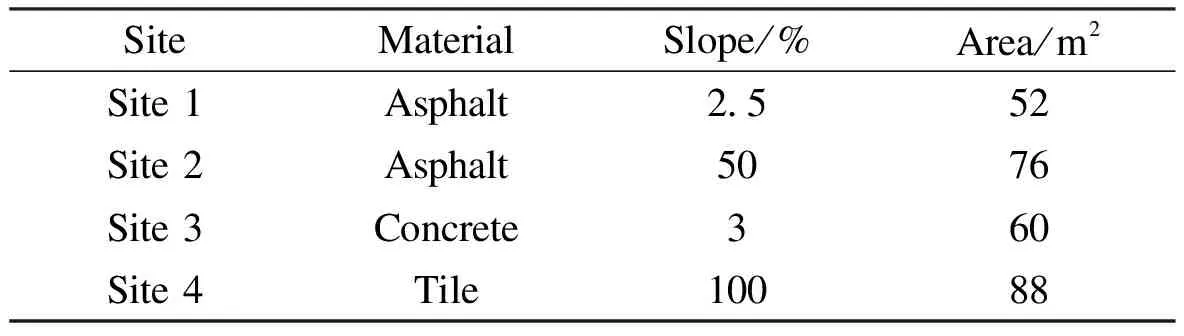
SiteMaterialSlope/%Area/m2Site1Asphalt2 552Site2Asphalt5076Site3Concrete360Site4Tile10088

The daily rainfall data (1960 to 2008) were obtained from the Meteorological Department of Handan. A telemetry rain gauge (SL1, China) was placed near all the study sites, by which the rainfall data were monitored from 116 rainfall events (2010 to 2012). The general information of monitored rainfall events is shown in Tab.2. Since the runoff losses are caused by infiltration and interception occur mainly at the initial rainfall, and first flush control is widely used in the RRHS for improving the rainwater quality[17-18], it is difficult to collect rainwater runoff during the initial rainfall or small rainfall (the depth is smaller than 5mm).

To estimate the roof runoff volume, a plastic tank with a capacity of 2 m3is used to store the roof rainwater. Two series-wound tanks are, respectively, connected with the vertical drain pipes of each selected roof, which may store at least 45 mm-depth rainfall in a single event. When the runoff volume exceeds the storage capacity of the plastic tank, the data of rainfall events are also excluded.

Tab．2 General information of rainfall events monitored in this study

YearAnnualrainfalldepth/mmNumberofmonitoredrainfallevents0to5mm5to15mm15to25mm25to35mm35to45mm>45mm2010516 7111464202011441 713843212012486 67146501Total1445．03136161242

2 Results and Discussion

2.1 Influence factors analysis ofψERC

For different rainfall events,ψERCcannot be determined as one constant, which is mentioned above. The major factors ofψERCdiscussed include the roof slope and material, the rainfall depth, and the intensity.

ψERCcan be calculated by the rational method, i.e.,

(1)

whereψERCis the value of ERC;Vis the volume of runoff,m3;V0is the volume of rainfall,m3;His the rainfall depth, mm;Ais the area of roof catchments, m2.

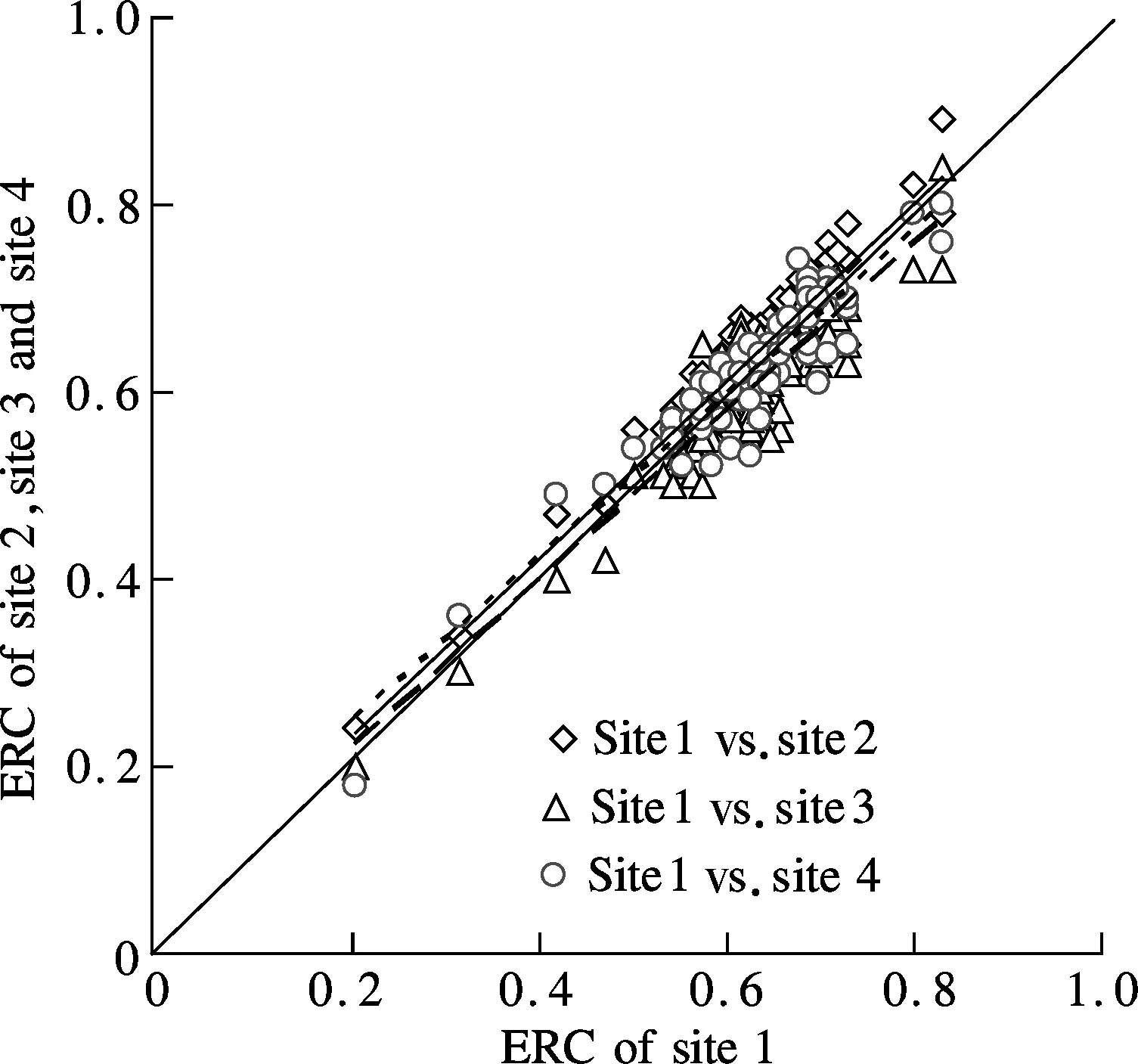
Fig.1 Comparison of ERC in different roof catchments

It is evident from Fig.1 thatψERCin different roof catchments is performed closely at the same rainfall event, so the linear correlations of the ERC of site 1 with that of other sites are analyzed and Pearson’s coefficient (r) is used for ranking the correlation. There is a strong correlation forψERCbetween different roof catchments. Pearson’s coefficient of site 1 vs. site 2, site 1 vs. site 3, and site 1 vs. site 4 is 0.932, 0.919, and 0.935, respectively. All the three fitting curves coincide with the diagonal.ψERCis less affected by roof slope and material. In other words,ψERCof different roof catchments can be regarded nearly as the same value in a certain event.

The relationship between ERC and event rainfall depth is shown in Fig. 2. In the most monitoring data of rainfall events,ψERCranges from 0.50 to 0.75, which strictly depends on the event rainfall depth. The rainfall events are classified by rainfall depth as shown in Tab. 2. At the class of 5 to 15 mm rainfall depth,ψERCgenerally increases with an increase in the event rainfall depth. It is because infiltration and interception losses for certain roof catchments in the initial stage of many rainfall events may have little difference. The lower the rainfall depth, the higher the proportion of infiltration and interception losses to rainfall. However, in other classes of rainfall events where rainfall depth exceeds 15 mm,ψERCfluctuates slightly on a small scale in each class. And with the increasing event rainfall depth,ψERCis presented as a stair-stepping decline in different classes. For the events of high rainfall depth, evaporation losses may be increased due to long rainfall duration. In comparison,ψERCin the events of 15 to 25 mm rainfall depth is much higher than that in other classes.

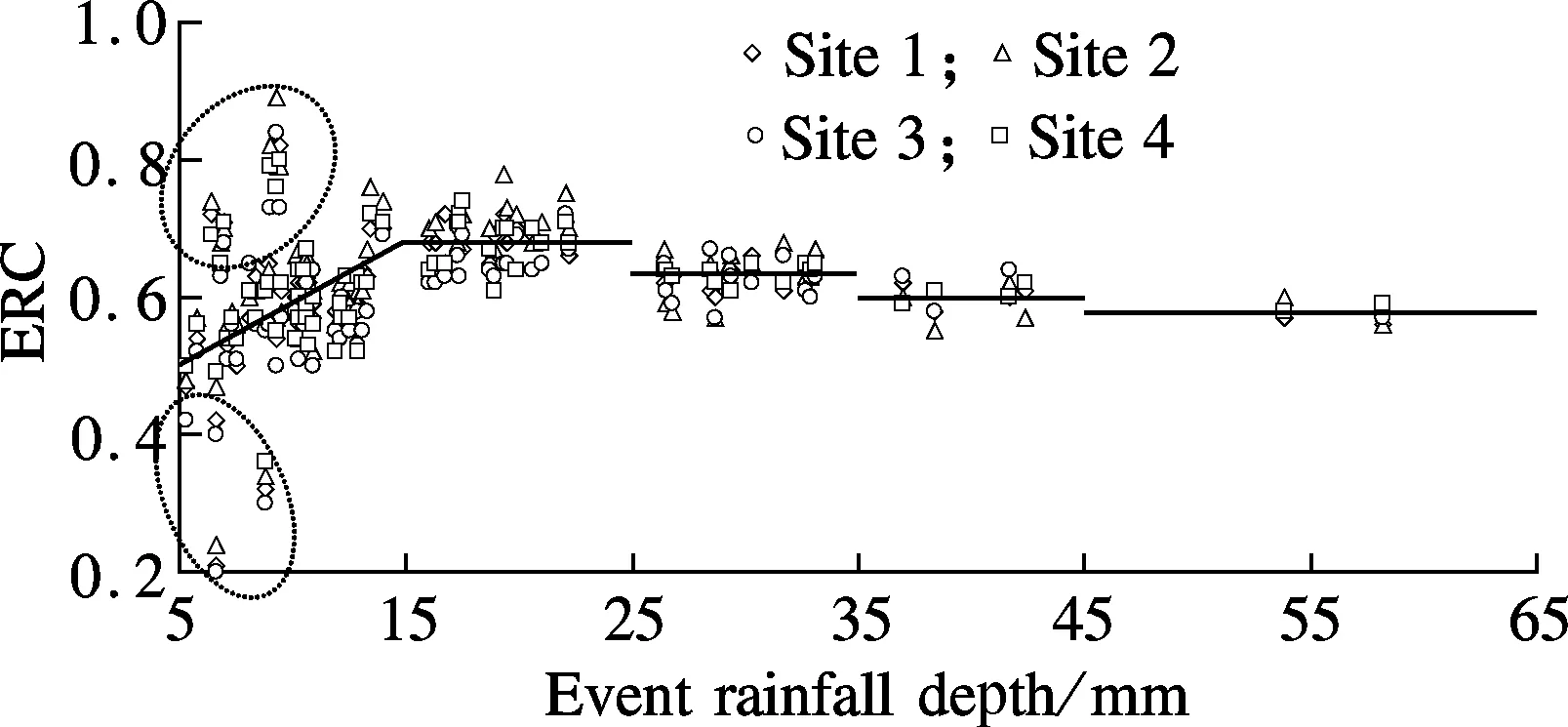
Fig.2 Relationship between ERC and event rainfall depth

Besides, the rainfall intensity is an important parameter for the runoff coefficient. The temporal variability of the rainfall intensity is almost random during a single event, by which the value of the runoff coefficient will fluctuate commonly[19]. However, the runoff coefficient affected by the rainfall intensity is an instantaneous flow runoff coefficient, while the ERC for RRHS is a volumetric runoff coefficient in a single event[20], soψERCis less influenced by the temporal variability of the rainfall intensity. The monitoring data of three events with almost the same rainfall depths and different mean rainfall intensities are shown in Tab.3. Because of high mean rainfall intensity,ψERCin event 2 is larger than those in event 1 and event 3. Though the mean rainfall intensities in event 1 and event 3 are different,ψERCis nearly equal. Based on the monitoring data, event 2 is a small probability rainfall event, which cannot be regarded as a general phenomenon to all the rainfall events. Therefore, the influence of the rainfall intensity on ERC can be ignored. The results are also verified by the data of other events in this study.

Tab．3 Influence of rainfall intensity on ERC

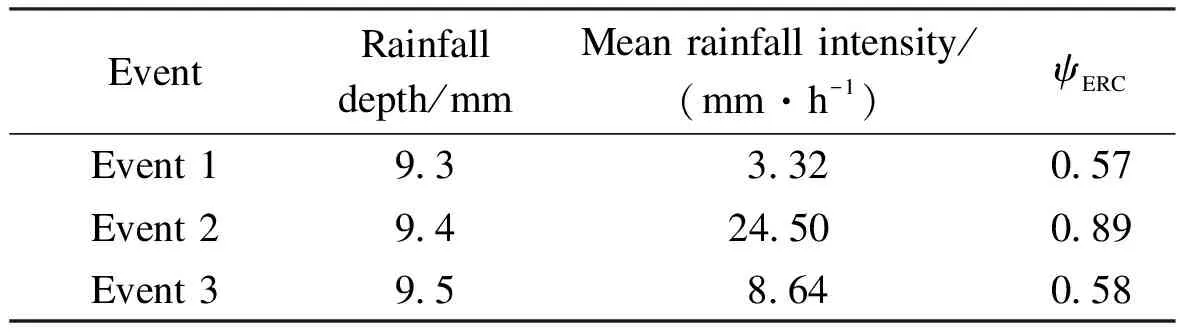
EventRainfalldepth/mmMeanrainfallintensity/(mm·h-1)ψERCEvent19 33 320 57Event29 424 500 89Event39 58 640 58

2.2 Determination ofψERC

According to the above results, the rainfall depth is a decisive factor for ERC, that is,ψERCcan be determined by the rainfall depth. In order to simplify the quantity assessment of RRHS,ψERCis empirically estimated by the piecewise linear function as follows:

(2)

As shown in Fig.2,ψERCis not the same in different rainfall classes. When the rainfall depth of an event is 5 to 15 mm,ψERCcan be calculated by a linear equation. For other classes (Rainfall depth is 15 to 25 mm, 25 to 35 mm, 35 to 45 mm or above 45 mm),ψERCis 0.68, 0.64,0.60 and 0.58, respectively.

In order to validate the suitability of the empirical equation above, the results of the comparison between observed ERC (ERCobs) from site 1 and estimated ones (ERCest) by Eq.(2) are presented in Fig.3. The pairs (ERCobs, ERCest) are well distributed near the diagonal line of perfect agreement except for the data of individual rainfall events. Therefore, the empirical equation (Eq.(2)) can be used to accurately estimate the ERC.

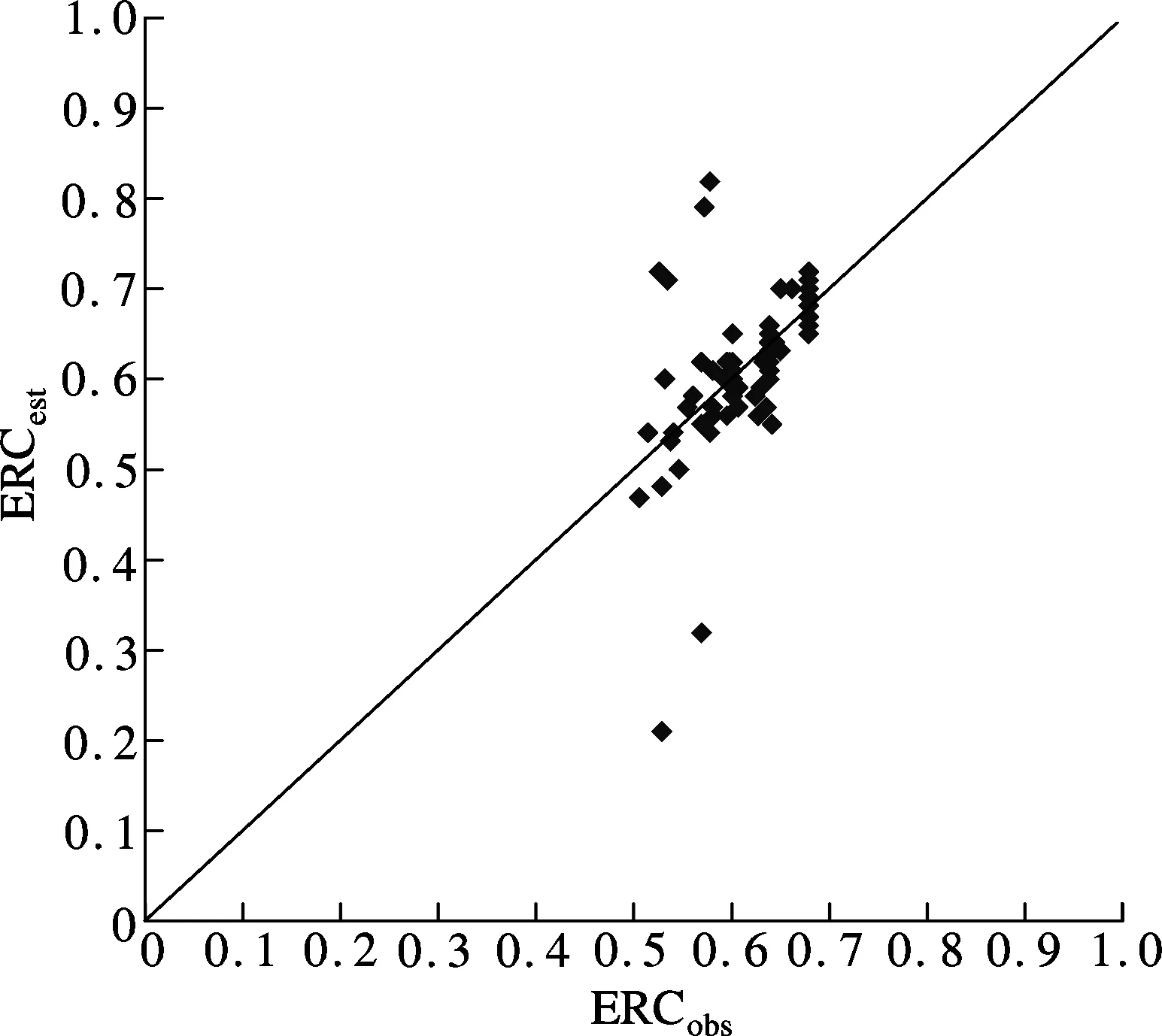
Fig.3 Comparison between ERCobs and ERCest

2.3 Determination ofψARC

To assess the annual available rainwater potential for the RRHS, ARC is determined by continuous simulations using daily rainfall data (1960 to 2008). Based on Eq.(2),ψERCfor each rainfall event can be determined using daily rainfall data. ARC of each year can also be obtained by continuous simulations according to the following equation:

(3)

whereψARCis the value of ARC;Hiis the rainfall depth of each event in a year,mm;ψERCiis the value of ERC atHidepth rainfall; ∑(HiψERCi) is the annual accumulative runoff depth, mm; ∑Hiis the annual accumulative rainfall depth, mm.

When the rainfall depth in a single event is less than 5 mm, it is difficult to generate the effective runoff on roof catchments for the RRHS. Therefore, the data of daily rainfall depth which is less than 5 mm are left out, that is, the values ofHiin Eq.(3) are more than 5 mm. Furthermore, annual rainfall data, which can be easily obtained from the meteorological department, are used to determine the ARC instead of annual accumulative rainfall. So, Eq.(3) can be written as

(4)

whereHais the annual rainfall depth, mm.

The relationship between ARC and annual rainfall is shown in Fig.4. Based on the daily rainfall data (1960 to 2008), the annual rainfall has a wide range. The highest annual rainfall depth was 1035.0 mm in 1963 and the lowest one was 313.9 mm in 1984. However, a dramatic result forψARCis presented in which a slight fluctuation near one constant (0.62) appeared, which was less influenced by the annual rainfall depth. 0.62 can be determined appreciatively asψARCin Handan. It can be widely used for the quantity assessment of the RRHS potential.

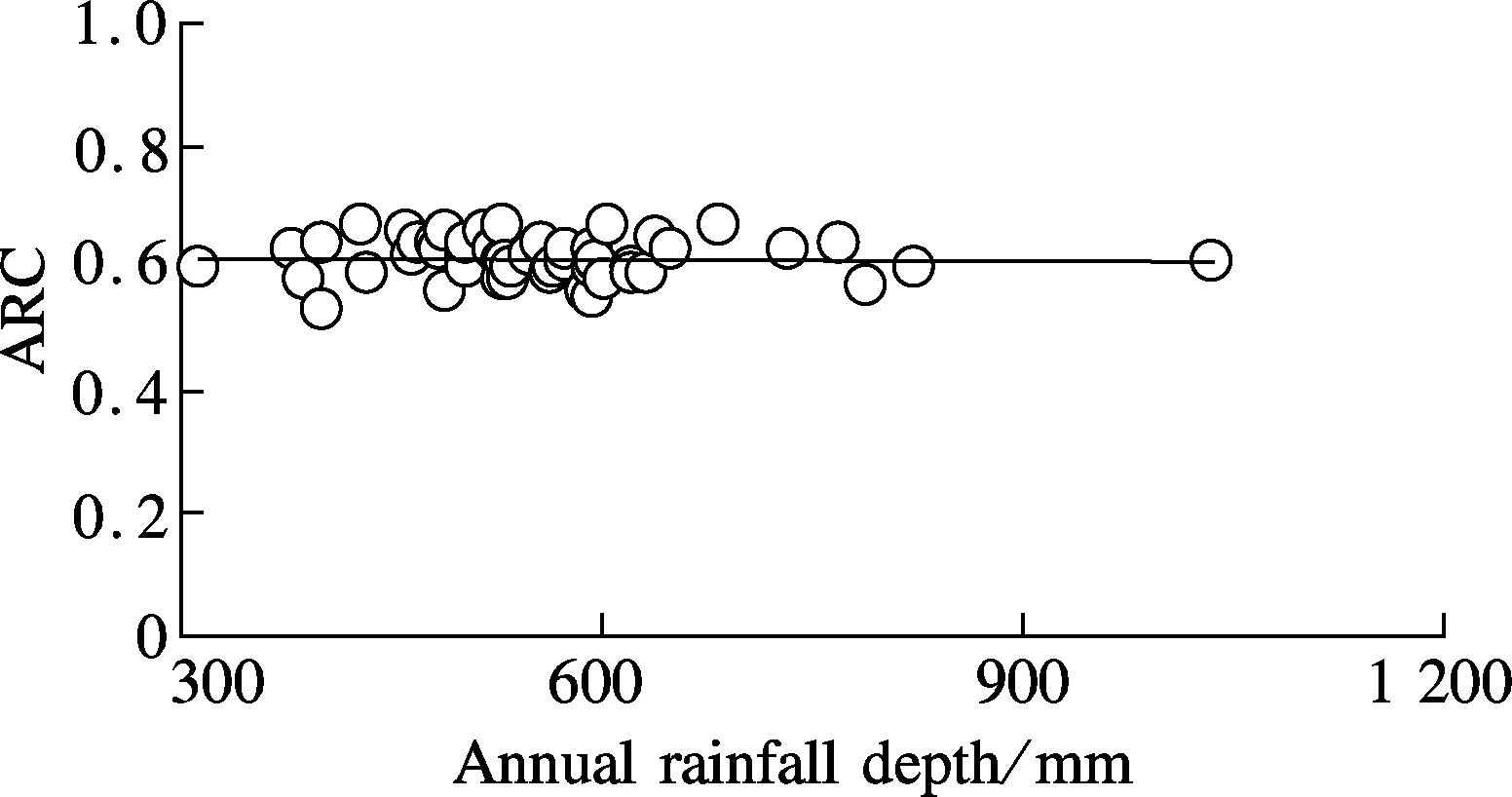
Fig.4 Relationship between ARC and annual rainfall

3 Conclusion

This paper focuses on the determiningψERCandψARCfor the quantity assessment of the RRHS in Handan, China. The results show that event rainfall depth is the controllable factor for ERC. Other factors, including roof slope, material and rainfall intensity, can be ignored. Based on the relationship between ERC and event rainfall depth, a simple method is developed for the determination ofψERCfrom the piecewise linear function. The ARC is also estimated by continuous simulations.ψARCof roof catchments in Handan is a constant, 0.62. The results of this paper are beneficial to improve the accuracy and simplification for the quantity assessment of RRHS in Handan.

[1]Guo Y, Baetz B W. Sizing of rainwater storage units for green building applications [J].JournalofHydrologicEngineering, 2007, 12(2): 197-205.

[2]Imteaz M A, Shanableh A, Rahman A, et al. Optimisation of rainwater tank design from large roofs: a case study in Melbourne, Australia [J].Resources,ConservationandRecycling, 2011, 55(11): 1022-1029.

[3]Campisano A, Modica C. Optimal sizing of storage tanks for domestic rainwater harvesting in Sicily [J].Resources,ConservationandRecycling, 2012, 63: 9-16.

[4]Ghisi E. Potential for potable water savings by using rainwater in the residential sector of Brazil [J].BuildingandEnvironment, 2006, 41(11): 1544-1550.

[5]Su M, Lin C, Chang L, et al. A probabilistic approach to rainwater harvesting systems design and evaluation [J].Resources,ConservationandRecycling, 2009, 53(7): 393-399.

[6]Farreny R, Morales-Pinzón T, Guisasola A, et al. Roof selection for rainwater harvesting: quantity and quality assessments in Spain [J].WaterResearch, 2011, 45(10): 3245-3254.

[7]Blume T, Zehe E, Bronstert A. Rainfall-runoff response, event-based runoff coefficients and hydrograph separation [J].HydrologicalSciencesJournal, 2007, 52(5): 843-862.

[8]Liaw C, Tsai Y. Optimum storage volume of rooftop rain water harvesting systems for domestic use [J].JournaloftheAmericanWaterResourcesAssociation, 2004, 40(4): 901-912.

[9]Khastagir A, Jayasuriya N. Optimal sizing of rain water tanks for domestic water conservation [J].JournalofHydrology, 2010, 381(3/4): 181-188.

[10]Aladenola O O, Omotayo B, Adeboye O B. Assessing the potential for rainwater harvesting [J].WaterResourcesManagement, 2010, 24(10): 2129-2137.

[11]Mun J S, Han M Y. Design and operational parameters of a rooftop rainwater harvesting system: definition, sensitivity and verification [J].JournalofEnvironmentalManagement, 2012, 93(1): 147-153.

[12]Norbiato D, Borga M, Merz R, et al. Controls on event runoff coefficients in the eastern Italian Alps [J].JournalofHydrology, 2009, 375(3/4): 312-325.

[13]Lancaster B.Rainwaterharvestingfordrylandsandbeyond,Vol. 1:guidingprinciplestowelcomerainintoyourlifeandlandscape[M]. Tucson: Rainsource Press, 2006: 42-44.

[14]van Dijk A, Bruijnzeel L A, Vertessy R A, et al. Runoff and sediment generation on bench-terraced hillsides: measurements and up-scaling of a field-based model [J].HydrologicalProcesses, 2005, 19(8): 1667-1685.

[15]Pandit A, Gopalakrishnan G. Estimation of annual storm runoff coefficients by continuous simulation [J].JournalofIrrigationDrainageEngineering, 1996, 122(4): 211-220.

[16]Baiamonte G, D’Asaro F, Grillone G. Empirical methods to determine average annual runoff coefficient in Sicilian basins [C/OL]//InternationalConferenceofAgriculturalEngineering. Valencia, Spain, 2012. http://m.cigr.ageng2012.org/images/fotosg/tabla-137-C1250.pdf.

[17]Zhang M, Chen H, Wang J, et al. Rainwater utilization and storm pollution control based on urban runoff characterization [J].JournalofEnvironmentalSciences, 2010, 22(1): 40-46.

[18]Gikas G D, Tsihrintzis V A. Assessment of water quality of first-flush roof runoff and harvested rainwater [J].JournalofHydrology, 2012, 466-467: 115-126.

[19]Wainwright J, Parsons A J. The effect of temporal variations in rainfall on scale dependency in runoff coefficients [J].WaterResourcesResearch, 2002, 38(12): 7-1-7-10.

[20]Tang N Y, Che W, Pan G Q. Runoff coefficient analysis for urban stormwater and flood control and utilization [J].ChinaWaterandWastewater, 2009, 25(22): 4-8. (in Chinese)

屋面雨水利用系統量化評估中徑流系數的取值

張 煒 李思敏 唐鋒兵

(河北工程大學城市建設學院, 邯鄲 056038)

為了實現屋面雨水利用系統量化評估中徑流系數的精確取值,通過連續3年(2010—2012年)對河北省邯鄲市不同屋面類型(屋面坡度和材料)及降雨特征(降雨深度和強度)的屋面徑流進行實地監測,得到了各場實際降雨屋面徑流系數的不同取值．研究結果表明,屋面徑流系數的取值分布與各降雨事件的降雨深度相關性較強,其他影響因素對其影響較小．場次徑流系數的取值與降雨深度呈顯著的分段線性關系．根據1960—2008年的日降雨數據資料,計算得出邯鄲市年均屋面徑流系數可近似按照0.62這一常數進行取值．該研究成果可用于屋面雨水利用系統的量化評估及運行分析．

屋面雨水利用系統;場次徑流系數;年均徑流系數;降雨深度

TV121

s：The National Science and Technology Major Project of China (No.2012ZX07203-003), the Major Basic Research Program of Hebei Province (No.12966738D), the Natural Science Foundation of Hebei Province (No.E2014402101).

：Zhang Wei, Li Simin, Tang Fengbing．Estimating runoff coefficient for quantity assessment of roof rainwater harvesting system[J]．Journal of Southeast University (English Edition),2014,30(2):220-224．

10.3969/j.issn.1003-7985.2014.02.015

10.3969/j.issn.1003-7985.2014.02.015

Received 2013-10-22．

Biography：Zhang Wei (1981—), male, master, lecturer, zhangwei1981@hebeu.edu.cn.