Mechanical properties of disc-spring vibration isolatorsbased on boundary friction

Jia Fang Zhang Fancheng

(School of Mechanical Engineering, Southeast University, Nanjing 210096, China)

?

Mechanical properties of disc-spring vibration isolatorsbased on boundary friction

Jia Fang Zhang Fancheng

(School of Mechanical Engineering, Southeast University, Nanjing 210096, China)

To ascertain the influence of the boundary friction on mechanical properties of disc-spring vibration isolators, a load-displacement hysteresis curve formula of disc-spring vibration isolators is derived on the basis of the energy conservation law, as well as considering the effect of the boundary friction. The formula is validated through the finite element analysis and static load tests. On this basis, the effect of the boundary friction on the bearing capacity is researched. Then the dynamic performance of disc-spring vibration isolators is studied by dynamic tests. The experimental results indicate that the boundary friction can promise a larger damping with a ratio of 0.23 for disc-spring vibration isolators. Compared with the loading frequency, the loading amplitude has a greater impact on the energy consumption, dynamic stiffness and damping of vibration isolators. This research can provide valuable information for the design of disc-spring vibration isolators.

disc-spring vibration isolator; boundary friction; hysteresis curve; dynamic stiffness; damping; finite element analysis (FEA)

The disc-spring vibration isolator features its small volume, large bearing capacity, variable stiffness and capability of providing friction damping by itself, thus winning a wide application in the field of nonlinear vibration isolation. Due to the existence of boundary friction, the loading/unloading curves of the vibration isolator do not overlap, which can bear much load on its mechanical properties.

Up to now, various researches have been focused on disc-springs and vibration isolators. Saini et al.[1]investigated the bearing capacity and deformation of disc springs with parabolically varying thickness by theoretical analysis. Fawazi et al.[2]studied the load displacement prediction for a bended slotted disc using the energy method. Curti et al.[3]studied the effect of friction on disc-spring calculation accuracy by the finite element method and experiments. Ozaki et al.[4]analyzed the performance of disc springs with different friction boundaries based on the energy method and the Coulomb friction theory. Xiong et al.[5]proposed a new type of vibration isolator composed of steel wire rope and disc springs and studied the dynamic response of the isolation system. Du et al.[6]explored the dynamic characteristics of a disc-spring shock absorber, pointing out that the shock absorber damping shows some of the nonlinear characteristics. Gong et al.[7]presented a new method for dynamic modelling of the vibration isolator addressing its hysteresis nonlinearity and better damping performance. Peng et al.[8]discussed the effects of cubic nonlinear damping on vibration isolations using the harmonic balance method. However, to the best of our knowledge, no attempt has ever been made to gain insights into the impact of boundary friction on the mechanical properties of disc-spring vibration isolators.

In the present study, a load-displacement hysteresis curve formula of disc-spring vibration isolators is developed, based on the theories or principles of energy conservation and boundary friction. Simulation based on finite element analysis (FEA) and static load tests are conducted for its verification. Dynamic performance of the disc-spring vibration isolator is studied through dynamic load tests. The findings are supposed to be of benefit to the desirable design of disc-spring vibration isolators.

1 Theoretical and Finite Element Analysis of Disc Springs

1.1 Theoretical analysis

The Almen-Laszlo equation[9]is currently a commonly-used formula for the disc spring design. However, it tends to generate conspicuous errors in solution as it ignores the boundary friction and the radial stress. In practice, the friction between stacked springs at the edges or on the surfaces will affect the stiffness estimation of the device due to large friction damping. The disc-spring structure of the vibration isolator is shown in Fig.1. Ignoring the boundary friction, the relationship between the loadP′ and deformationfcan be written as[10]

(1)

Fig.1 Structure diagram of disc spring

ParameterValueElasticmodulusE/Pa2.06×1011Poissonratioν0.3OuterradiusR/mm225Innerradiusr/mm112Thicknesst/mm6.5Freeheighth0/mm7.1

To ascertain the relationship of the frictional dissipation and the deformation, a free body diagram of the disc spring with friction force is presented in Fig.2. In terms of the Almen-Laszlo assumptions, the cross section of the disc spring does not distort, and it merely rotates about a neutral point; thus the sliding displacement in the radial direction and the rotation angleαof the cross section can be expressed by[4]

(2)

wherelis the diagonal length of the cross section;βis the angle between the diagonal and vertical planes. As it is difficult to obtain the actual force acting on the boundary, the friction pressure is replaced by loadp′ in our finite element analysis. When the deformation of the disc spring rises to df, an extra loadp*is required to over-come the frictional energy dissipation. By the law of energy conservation, the frictional energy dissipation should be equal to the work done by the extra load; that is

Fig.2 Force sketch of single disc spring

W=Ef, dW=dEf

(3)

dW=p*df

(4)

dEf=2Fedse=2p′μdse

(5)

whereWis the extra work;Efis the frictional energy dissipation; dW, dEfrepresents the infinitesimal increment;Feis the frictional force; andμis the friction coefficient. As the rotation angleαis very small, Eq.(2) can be simplified into

(6)

And the relationship between the frictional displacement and the deformation is

(7)

Based on Eqs.(3), (4), (5) and (7), the width of the load-displacement hysteresis curve can be calculated by

(8)

Thus, we obtain the load-displacement hysteresis curve formula of the single disc spring as follows:

(9)

where “+” is for loading and “-” for unloading.

1.2 Frictional analysis of disc-spring vibration isolators

The disc-spring vibration isolator can be designed by arranging disc-springs in series or in parallel for different loads. And there must exist friction at the edges and on the surfaces between parallel springs. The structure of the vibration isolator is shown in Fig.3, whereJrepresents the number of disc springs in parallel andIdenotes the number of series of disc springs. A steel plate is used to connect disc-springs in series. Ignoring the friction, the load of the isolator isJp′ when the deformation isIf. In addition, the surface friction displacementsscan also be evaluated as a function of the deformationf. As illustrated in Fig.3, the surface friction displacement is given as

(10)

whereA(x1,y1) andB(x1,y2) are the coordinates at the contact points of disc springs stacked in parallel, which vary with the deformation of the springs. Known from the

Fig.3 Structure of disc-spring vibration isolator (I=2,J=2,O1(xo1,yo1) andO2(xo2,yo2))

researches on the single disc spring, the contact points rotate about the neutral pointO. So based on the coordinate transformation matrix, the rotation matrix of pointsAandBcan be written as

wherexo2=xo1;yo2=yo1+t/sinφ, andφis the angle between the spring and the vertical plane. During the deformation, the location vectors {x1,y1,1} and {x2,y2,1} change with the rotating neutral pointsO1andO2. According to Eqs.(10), (11) and (12), the surface friction displacement can be calculated by

When the deformation of the vibration isolator grows to df, the friction energy dissipation and the extra force overcoming the surface friction can be denoted as

(14)

(15)

And the extra force overcoming the edge friction is

(16)

Thus, we obtain the load-displacement hysteresis curve formula of the disc-spring vibration isolator as

(17)

where “+” is for loading and “-” for unloading.

1.3 Finite element analysis

ANSYS 12.0 is used to analyze the static-load characteristics of a single disc spring and two disc springs in parallel. The FEA models are demonstrated in Fig.4. The axial displacement load is imposed on the top of the models for transient dynamic analysis. Then the loading and unloading conditions with different friction coefficients are simulated to validate the hysteresis curve formula. The results from FEA and the hysteresis curve formula are compared in Figs.5 and 6. As illustrated in Fig.5, similar changes are observed among the results from the FEA, the hysteresis curve formula and the theoretical curve. No overlapping is observable between the loading and unloading curves due to the presence of friction. Fig.6 shows that with the surface friction added, the curves of the FEA and the hysteresis curve formula remain highly consistent. This verifies the accuracy of the formula.

(a) (b)

Fig.4 FEA models of disc spring. (a) Single disc spring; (b) Two disc springs in parallel

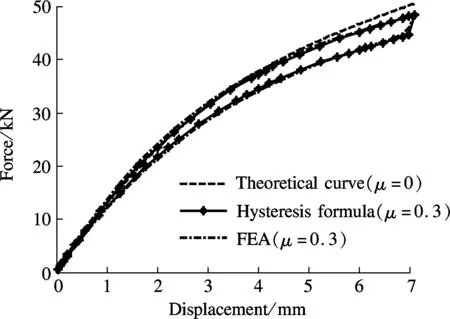
Fig.5 Loading-displacement of the single disc spring

Fig.6 Loading displacement of two disc springs in parallel (μ=0.3)

2 Static Experiment and Analysis

To evaluate the effect of boundary friction on the isolator’s static stiffness, static load deformation resistibility and dynamic features, an intelligent servo hydraulic testing machine is used to carry out the test. The test system consists of the loading test system and the data collection system, as shown in Fig.7. As the disc-spring vibration isolator is composed of two disc springs set in parallel and four groups in series, the same mechanical properties are shared by all the groups. The load-displacement curves of the experiments, the FEA and the hysteresis curve formula are compared in Fig.8, which shows that the theoretical curves differ a lot from the test curves in the initial phase of deformation. With the increase of deformation, the difference gradually narrows. This is because error exists in the assembly process of disc springs. It also shows that the area of load-deformation curves in the experiment is approximately equal to that in the formula with the friction coefficient of 0.3. Therefore, 0.3 can be taken as the boundary friction coefficient of the disc-spring vibration isolator.

Fig.7 Mechanical test system

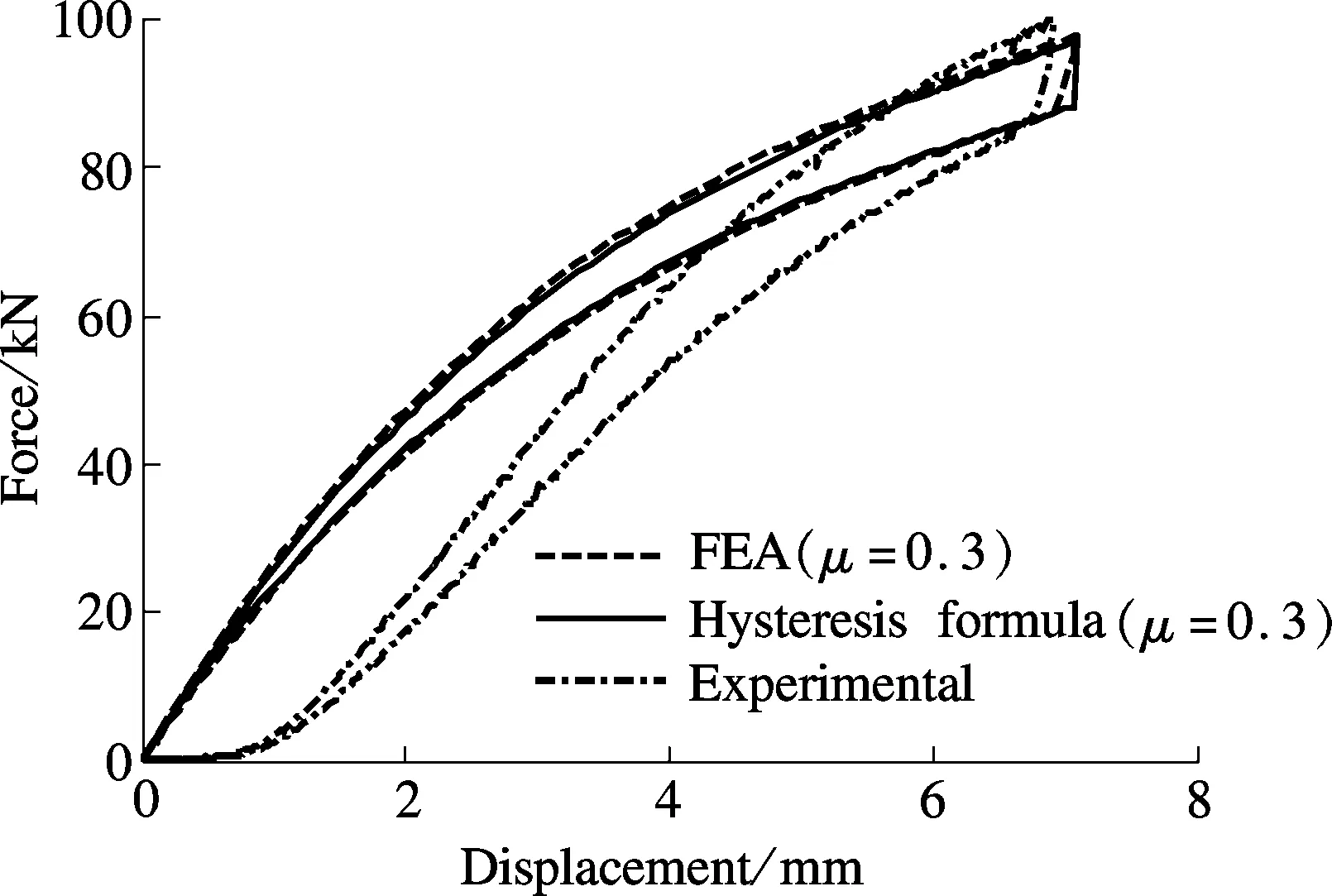
Fig.8 Loading displacement of static load experiment

The loading and unloading stiffnesses of the disc-spring vibration isolator are derived from numerical analysis. CFTOOL, a fitting tool in Matlab, is used to fit the loading/unloading stiffness curves of the experiment. Then the results from the experiment, the hysteresis formula and the theoretical analysis are compared in Fig.9. As shown in Fig.9, the loading and unloading stiffnesses given by the test and the formula are lower than that of the theoretical result which ignores the friction effect. It is a solid evidence that the boundary friction can reduce the stiffness of the disc-spring vibration isolator. The averages of the loading and unloading stiffnesses in different deformations from the theoretical calculation and test results can well reflect the static stiffness of the vibration isolator. The average values of stiffness from the hysteresis formula and the tests are compared. Results show that the maximum and minimum deviations of calculated values and test values are 7.6% and 1.2%, respectively, which proves that the hysteresis formula is of high accuracy and it is capable of reflecting the static load performance of disc-spring vibration isolators accurately.

(a)

(b)Fig.9 Loading/unloading stiffness of disc-spring vibration isolator. (a) Loading stiffness; (b) Unloading stiffness

3 Dynamic Experiment and Analysis

Dynamic stiffness and damping are the key parameters to the design of vibration isolators. Dynamic stiffness reflects the device’s ability to resist deformation under dynamic load, and damping is its capability for energy dissipation. To ascertain the impact of the boundary friction on its dynamic performance, a 50 kN pre-load is slowly applied onto the vibration isolator, followed by the sinusoidal displacement control with the amplitudes of 0.5, 1 and 2 mm and the frequencies of 3, 4 and 5 Hz to obtain its force response.

3.1 Results of dynamic experiment

Results of the dynamic experiment are demonstrated in Figs.10 and 11. As illustrated in Fig.10, with the increasing amplitude, the areas of the hysteretic curves expand. In other words, the larger the displacement, the more the dissipated energy. As shown in Fig.11, with the change of loading frequency, the curve areas remain nearly invariable, which means that the loading frequency has little influence on the ability of energy consumption. For further study, dynamic stiffnessKeand equivalent damping coefficientξeare calculated using the following equations[11]and presented in Tab. 2.

(18)

(19)

whereu+andu-denote the largest and the least vertical deformation;f+andf-represent the vertical forces corresponding tou+andu-; andSis the area of the hysteresis curve.

Fig.10 Hysteretic curves of different amplitudes with a loading frequency of 5 Hz

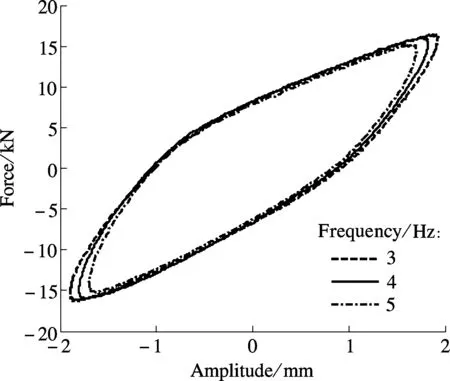
Fig.11 Hysteretic curves of different frequencies with an amplitude of 2 mm

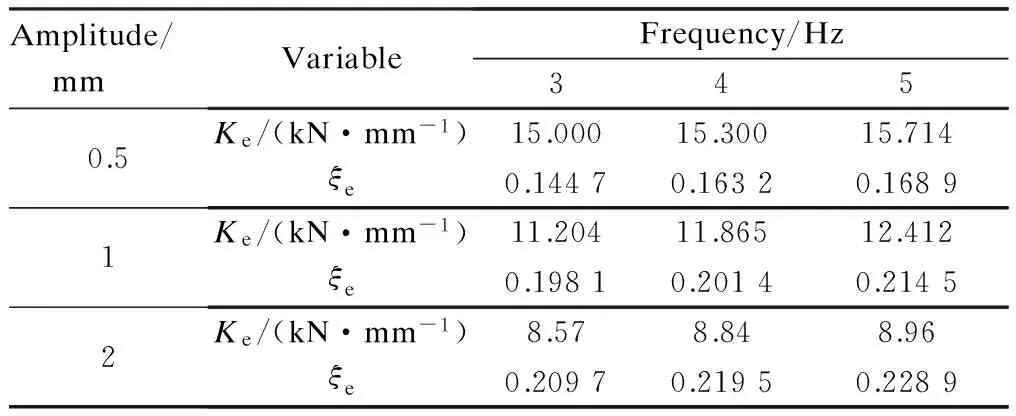
Amplitude/ mmVariableFrequency/Hz3450.5Ke/(kN·mm-1)15.00015.30015.714ξe0.14470.16320.16891Ke/(kN·mm-1)11.20411.86512.412ξe0.19810.20140.21452Ke/(kN·mm-1)8.578.848.96ξe0.20970.21950.2289

3.2 Analysis of dynamic performance

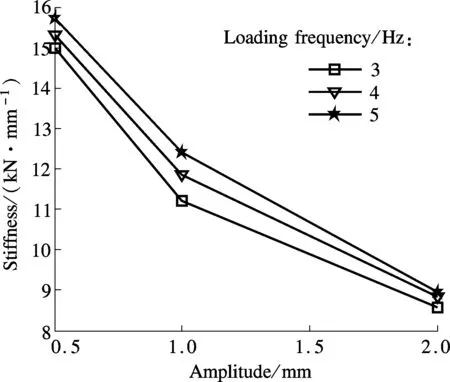
The effect of amplitude on the dynamic stiffness and the equivalent damping ratio is presented in Fig.12. As can be observed, the dynamic stiffness decreases with the increasing loading amplitude while the loading frequency remains constant, which fully reflects the nonlinearity of the disc-spring vibration isolator. In contrast, the equivalent damping ratio rises with the increasing load amplitude, but the rising trend dwindles away gradually. When the amplitude grows from 0.5 to 1 mm and from 1 to 2 mm, the damping ratio goes up by 36.9% and 5.89%, respectively. Apparently, as the damping of the vibration isolator is provided by the boundary friction that relates to the friction coefficient, force and amplitude, it is only af-fected by the amplitude when the friction coefficient and force are invariant. That is why the disc-spring vibration isolator can provide a larger friction damping of up to 0.23.

(a)

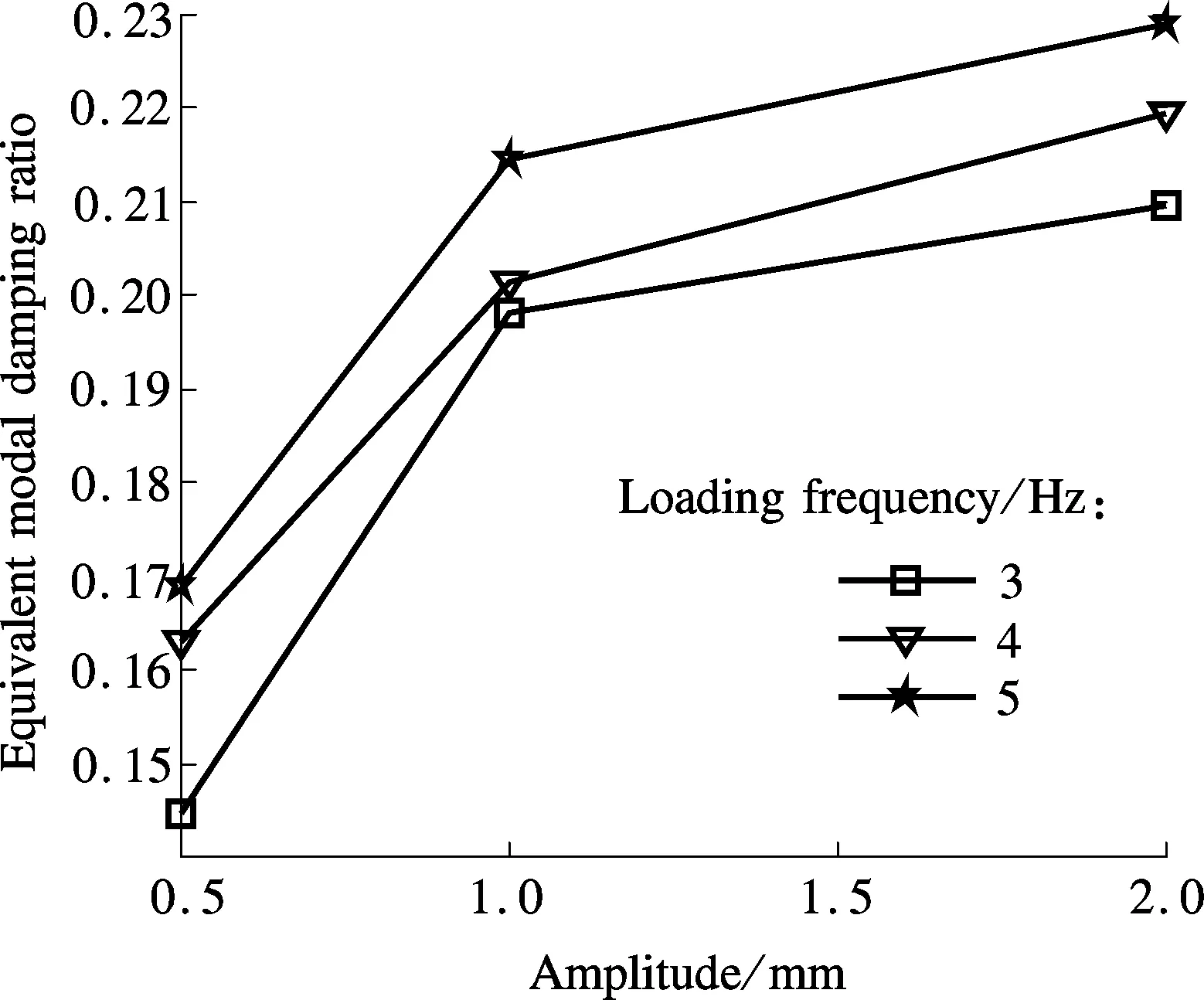
(b)Fig.12 Dynamic performance. (a) Dynamic stiffness; (b) Equivalent damping ratio

Fig.12 also shows that with constant loading amplitude both the dynamic stiffness and the equivalent damping ratio feature a trend of gradual rise with the increase of loading frequency. That is to say, the loading amplitude has a greater effect on the dynamic stiffness and the equivalent damping ratio of the vibration isolator than the loading frequency. It means that the vibration amplitude is a key parameter to the properties of the disc-spring vibration isolator.

4 Conclusion

In the present study, a load-displacement hysteresis curve formula of the disc-spring vibration isolator which considers the boundary friction is developed based on the principles of energy conservation. The validity of the formula is verified and the influence of boundary friction on the static stiffness is also investigated via the finite element simulation and static load tests. The effect of the boundary friction on the isolator dynamic performance is also studied. As revealed by the test results, the boundary friction endows the disc-spring vibration isolator with a larger damping of nearly 0.23. The loading amplitude exerts a larger influence on the isolator’s energy dissipation, dynamic stiffness and damping coefficient than the loading frequency does. This research may provide valuable information for the design of the disc-spring vibration isolator.

[1]Saini P K, Kumar P, Tandon P. Design and analysis of radially tapered disc springs with parabolically varying thickness[J].JournalofMechanicalEngineeringScience, 2007, 221(2): 151-158.

[2]Fawazi N, Lee J, Oh J. A load-displacement prediction for a bended slotted disc using the energy method[J].JournalofMechanicalEngineeringScience, 2012, 226(8): 2126-2137.

[3]Curti G, Montanini R. On the influence of friction in the calculation of conical disk springs[J].JournalofMechanicalDesign, 1999, 121(4): 622-627.

[4]Ozaki S, Tsuda K, Tominaga J. Analyses of static and dynamic behavior of coned disk springs: effects of friction boundaries[J].Thin-WalledStructures, 2012, 59: 132-143.

[5]Xiong Shishu, Li Huisheng, Huang Liting, et al. Design and application of base isolation system for explosive laboratory[J].ExplosionandShockWaves, 2006, 26(2): 145-149. (in Chinese)

[6]Du Junmin, Dai Shuangxian. Research on dynamic characteristics of saucer dampers[J].ConstructionMachineryandEquipment, 2009, 40(11): 15-18. (in Chinese)

[7]Gong Xiansheng, Xie Zhijiang, Luo Zhenhuang, et al. The characteristics of a nonlinear damper for vibration isolation[J].JournalofVibrationEngineering, 2001, 14(3): 90-94. (in Chinese)

[8]Peng Z K, Meng G, Lang Z Q, et al. Study of the effects of cubic nonlinear damping on vibration isolations using harmonic balance method[J].InternationalJournalofNon-LinearMechanics, 2012, 47(10): 1073-1080.

[9]Almen J O, Laszlo A. The uniform-section belleville spring[J].TransASME, 1936, 58(5): 387-392.

[10]Yi Xianzhong. Analysis of basic characteristic parameters of disk springs [J].ChinaPetroleumMachinery, 1995, 23(3): 10-17. (in Chinese)

[11]Chen Heshi. Experimental study of nonlinear assembled isolator for high speed press[D]. Nanjing: School of Mechanical Engineering of Southeast University, 2011. (in Chinese)

基于邊界摩擦的碟簧隔振器力學(xué)性能

賈 方 張凡成

(東南大學(xué)機(jī)械工程學(xué)院,南京 210096)

為研究邊界摩擦對(duì)碟簧隔振器力學(xué)性能的影響,基于能量守恒定律推導(dǎo)了在考慮邊界摩擦?xí)r碟簧隔振器的載荷位移遲滯曲線公式.通過(guò)有限元分析與靜載試驗(yàn)驗(yàn)證了該公式的正確性.在此基礎(chǔ)上研究了邊界摩擦對(duì)碟簧隔振器承載能力的影響,并通過(guò)動(dòng)載試驗(yàn)研究了邊界摩擦對(duì)碟簧隔振器的動(dòng)態(tài)性能的影響.試驗(yàn)結(jié)果表明:邊界摩擦可提供較大的阻尼,使得碟簧隔振器具有良好的阻尼特性,其阻尼比可達(dá)0.23;隔振器的耗能、動(dòng)剛度和阻尼特性對(duì)加載幅值更為敏感,而對(duì)加載頻率敏感度較小.該研究成果對(duì)碟簧隔振器設(shè)計(jì)具有重要的指導(dǎo)意義.

碟簧隔振器;邊界摩擦;遲滯曲線;動(dòng)剛度;阻尼;有限元分析

TP391

Transformation Program of Science and Technology Achievements of Jiangsu Province (No.BA2008030).

：Jia Fang, Zhang Fancheng. Mechanical properties of disc-spring vibration isolators based on boundary friction[J].Journal of Southeast University (English Edition),2014,30(1):39-44.

10.3969/j.issn.1003-7985.2014.01.008

10.3969/j.issn.1003-7985.2014.01.008

Received 2013-08-07.

Biography：Jia Fang (1968—), female, doctor, associate professor, 13851896116@139.com.