基于邊緣接觸時變剛度的輪齒表面剝落動力學模型與響應特征

邵毅敏, 王新龍, 劉 靜, 陳再剛

(重慶大學 機械傳動國家重點實驗室，重慶 400030)

嚙合接觸剛度是齒輪系統中影響系統動態響應的重要因素，目前的研究集中在輪齒故障的動態特性計算方面[1-3]，針對齒面剝落輪齒在嚙出時，剝落邊界和對應輪齒齒面發生邊緣接觸作用，以及這種邊緣接觸作用對嚙合剛度及其動態響應的影響和能量傳遞的影響等研究較少。

本文考慮邊緣接觸作用，建立了“復合剛度計算模型”，提出了輪齒表面剝落缺陷的時變剛度算法，計算了剝落擴展過程中的不同剝落界面形貌的邊緣接觸時線接觸彈性接觸剛度和嚙合剛度，通過對時變信號和頻譜的分析，研究了存在表面剝落的齒輪系統動態響應特征。獲得了表面剝落對于齒輪系統動態響應的影響特性。

1 輪齒表面剝落缺陷的時變剛度算法

表面剝落缺陷輪齒與正常輪齒嚙合過程中，在嚙出剝落邊界時，與其邊緣發生接觸作用，導致齒面接觸力產生突變，直接影響齒對嚙合動態特性，因此，分析邊緣接觸問題，建立考慮邊緣接觸的嚙合剛度計算模型，是研究表面剝落對嚙合剛度及其動態響應影響的重要問題。

本文提出的復合剛度計算模型是同時包含基于勢能原理的嚙合剛度計算模型與邊緣接觸剛度計算模型的綜合嚙合剛度計算模型。

1.1 輪齒表面剝落的復合接觸剛度模型

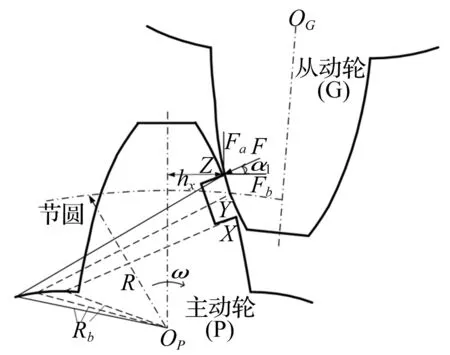
圖1 表面剝落齒對嚙合示意圖

表面剝落齒對嚙合，如圖1所示。剝落區域按照嚙合線法向和切向投影得到齒對嚙合過程中剝落區域的接觸過程示意圖，如圖2和圖3所示。其虛線表示發生邊緣接觸位置。表面剝落齒對嚙合過程接觸剛度情況，如圖4所示，Kn、Ks分別表示沿齒寬方向的漸開線接觸剛度、邊緣接觸剛度。

(1) 在進入剝落邊界之前的正常齒面區域，齒對的嚙合通過漸開線齒面線接觸嚙合，接觸剛度包括沿齒面方向的Kn(如圖4(a))；

(2) 在剝落且非邊界區域(如圖2(b), 嚙合點Y)，齒面與剝落輪齒兩端齒面通過漸開線接觸嚙合，接觸剛度包括兩端的Kn(如圖4(b))；

(3) 在嚙出剝落邊界時(如圖2(c), 嚙合點Z)，齒面與剝落邊界邊緣發生接觸，導致接觸力產生突變，同時齒面與非剝落區域產生漸開線接觸，接觸剛度包括Kn、Ks(如圖4(c))；

(4) 齒對嚙合離開剝落區域，接觸情況和(1)相同(如圖4(d))。因此表面剝落齒對嚙合的接觸過程存在一邊-兩邊-三邊-一邊的變化過程，所以，嚙合剛度K(t)的計算必須要用分段函數表示。

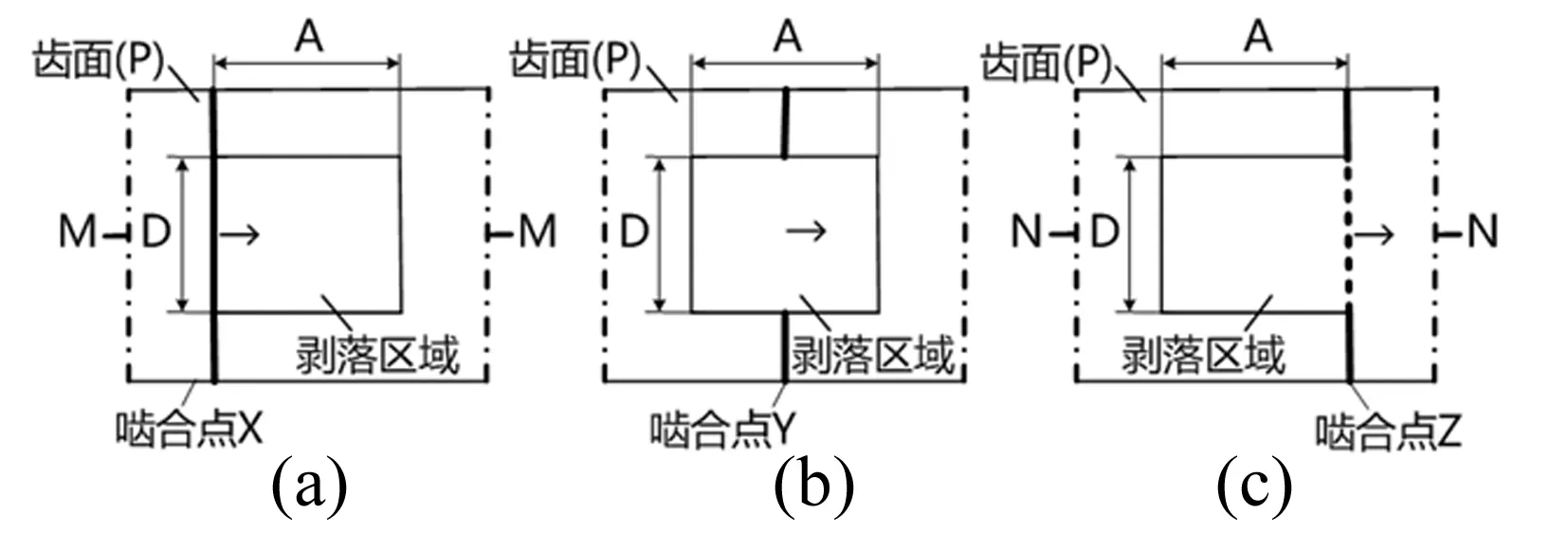
圖2 剝落區域齒對嚙合法向示意圖

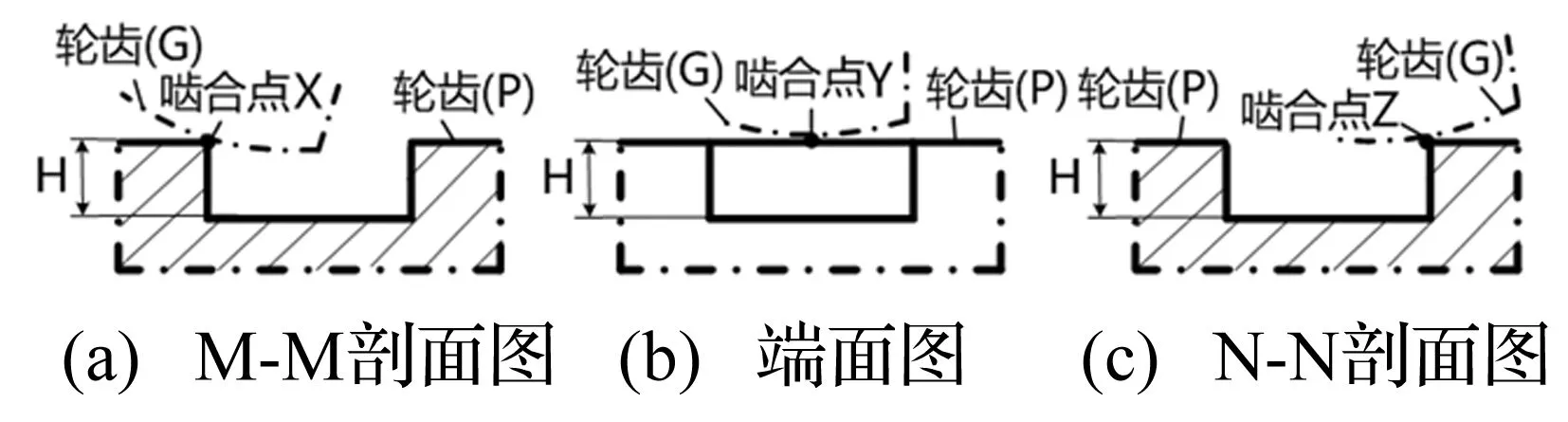
圖3 剝落區域齒對嚙合切向示意圖

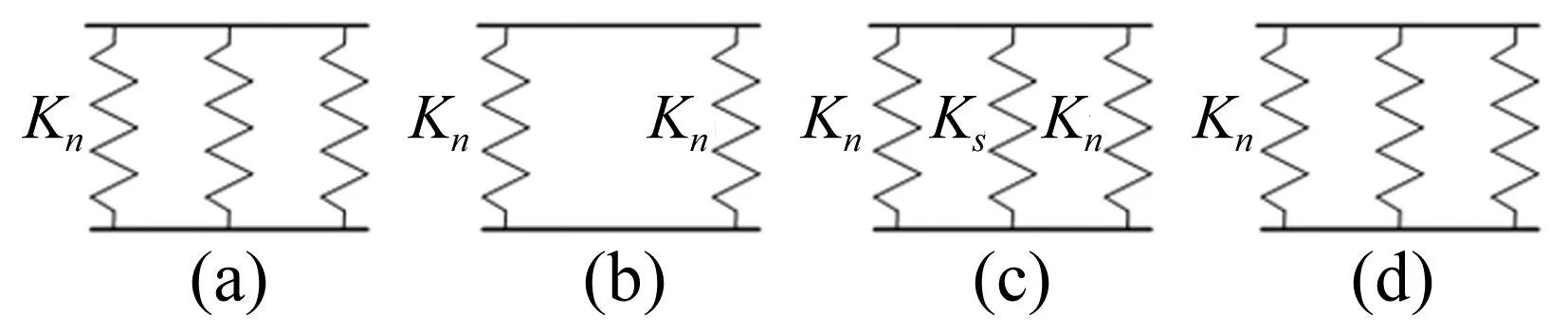
圖4 表面剝落齒對嚙合過程接觸剛度示意圖

齒對嚙合剛度[6]可以表示為式(1)，其中Kh、Kb、Ks、Ka、Kf分別表示接觸剛度、彎曲剛度、剪切剛度、軸向壓縮剛度、基體變形剛度。

K(t)=

(1)

式中:Rs表示剝落邊界漸開線曲率半徑，Rs在剝落擴展的過程中保持常量特性。利用線接觸彈性接觸變形的解析算法[4,5]，計算邊緣接觸剛度，計算有限長線接觸相對應的計算參數ε:

(π/2-θ1)/ε=(π/2-arccosε)/ε=1

(2)

與接觸區域相關的面積系數的計算：

Δ1=(f0-f1)(π/2-θ1)/2

(3)

Δi=(fi-1-fi+1)(θi-θi+1)/2

(4)

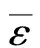
(5)

離散積分：

(6)

光滑彈性體接觸理論中的法向接觸變形計算式為：

δs=ηbp0Kθ1

(7)

式中：η表示和接觸體材料屬性有關的特性系數：

(8)

Kθ1表示第一類全橢圓積分, 其計算式為：

(9)

由式(6)和式(9)，可獲得Kθ1的簡化計算方程：

(10)

p0表示接觸區最大接觸壓力, 計算式為：

p0=3P/(2πLab)

(11)

其中：

(12)

(13)

∑ρ表示主曲率之和：

(14)

漸開線齒對嚙合的接觸剛度沿整個接觸線上可視為近似常數[9]。漸開線齒對嚙合接觸剛度的計算采用式(15)，由式(15)和式(7)可得復合接觸剛度式(16):

(15)

(16)

則齒對在整個嚙合過程的復合接觸剛度Kh計算式表示為如下分段函數：

(17)

式中:α1、αI、αO、LsH、W分別表示任意嚙合壓力角、嚙入剝落邊界壓力角、嚙出剝落邊界壓力角、非剝落輪齒長度、輪齒寬度。

將輪齒視為變截面懸臂梁計算直齒輪輪齒嚙合過程的Kb、Ks、Ka、Kf，則齒對嚙合的彎曲、剪切和軸向壓縮剛度計算式可以表示為[2,6]：

(18)

(19)

齒輪基體變形對于時變嚙合剛度有重要影響，Sainsot等[7]計算得出基體變形剛度計算式：

(20)

(21)

綜合上述，將復合接觸剛度Kh及Kb、Ks、Ka、Kf計算式帶入嚙合剛度公式(17)，并設：

(22)

則整個嚙合過程的復合剛度計算式表示為如下分段函數K(t):

(23)

文獻[6, 8]分片積分計算法，將剝落模型分成正常、故障兩部分分別計算變形剛度，整個輪齒的剛度可以將嚙合剛度在整個輪齒齒寬W積分獲得：

(24)

1.2 接觸剛度計算模型驗證

為了驗證本文邊緣接觸剛度計算模型的正確性，建立了相應的有限元分析模型。利用有限元法和本文提出的邊緣接觸剛度算法分別計算了存在齒面剝落故障的齒輪嚙合副邊緣接觸剛度，其結果如圖5所示。圖5顯示了四種不同剝落寬度的8組邊緣接觸剛度計算結果。兩者計算結果一致，最大誤差僅為4.54%，證明了本文提出的邊緣接觸剛度計算模型的正確性。

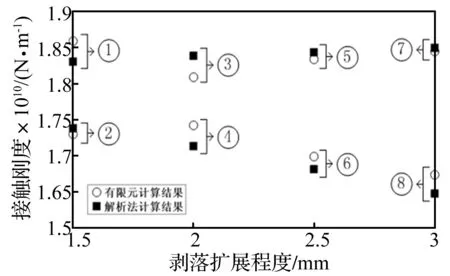
圖5 復合接觸剛度算法結果與有限元計算結果

2 仿真計算條件及仿真結果

2.1 仿真條件

仿真的系統參數，如表1所示。仿真分析輪齒表面剝落缺陷位于小齒輪，表面剝落參數，如表2所示。

2.2 仿真結果

不同剝落寬度(D=45 mm,H=1.0 mm)影響的單雙齒對嚙合剛度曲線、不同剝落長度(A=3 mm,H=1.0 mm)影響的單雙齒對嚙合剛度曲線，分別如圖6和圖7、圖8和圖9所示。橫坐標為嚙合壓力角，實線方塊、虛線方格分別表示考慮邊緣接觸“與”“否”的計算結果，計算結果顯示：隨著剝落寬度擴展，嚙合剛度曲線出現明顯衰減現象，而最大的衰減出現在存在剝落缺陷的輪齒退出嚙合的位置，特別是齒對在嚙出剝落邊界時，由于邊緣接觸作用的影響，導致嚙合剛度發生突變現象。

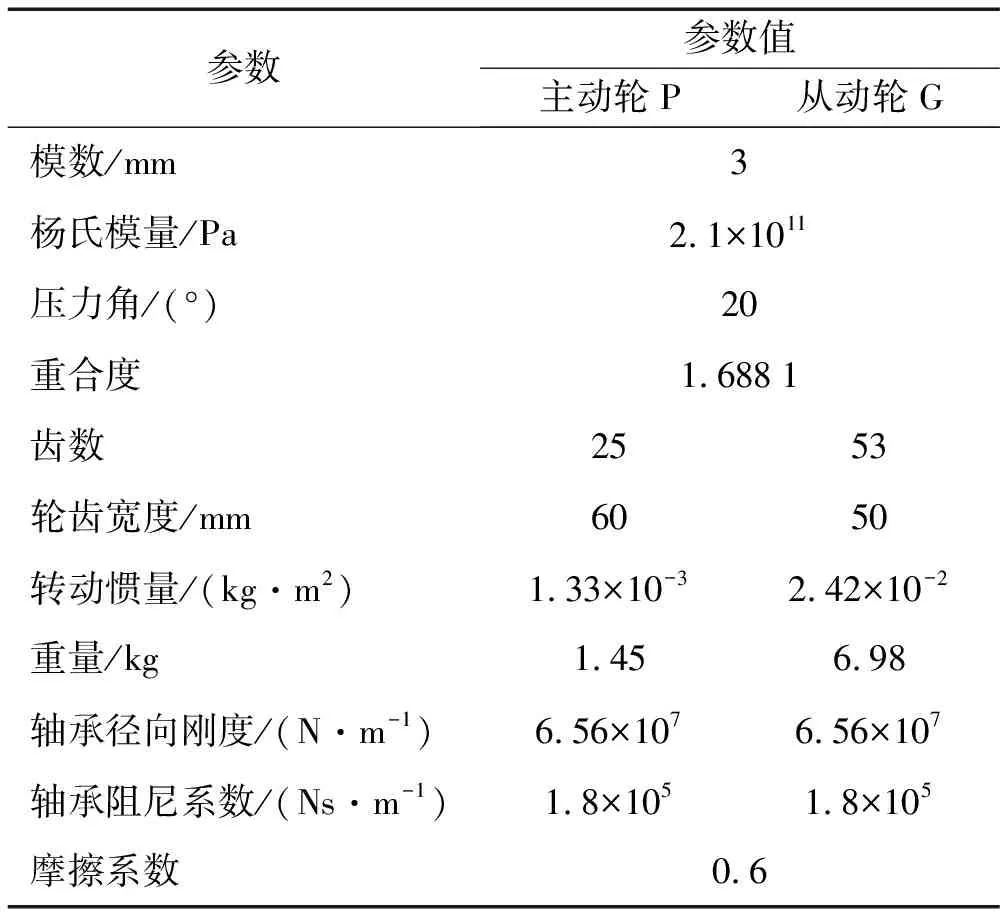
表1 齒輪系統參數

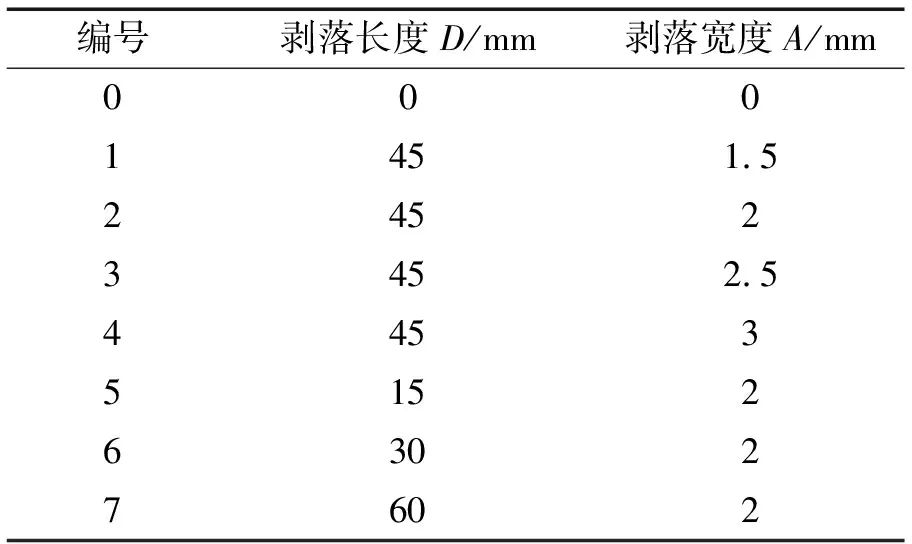
表2 小輪齒表面剝落缺陷仿真參數

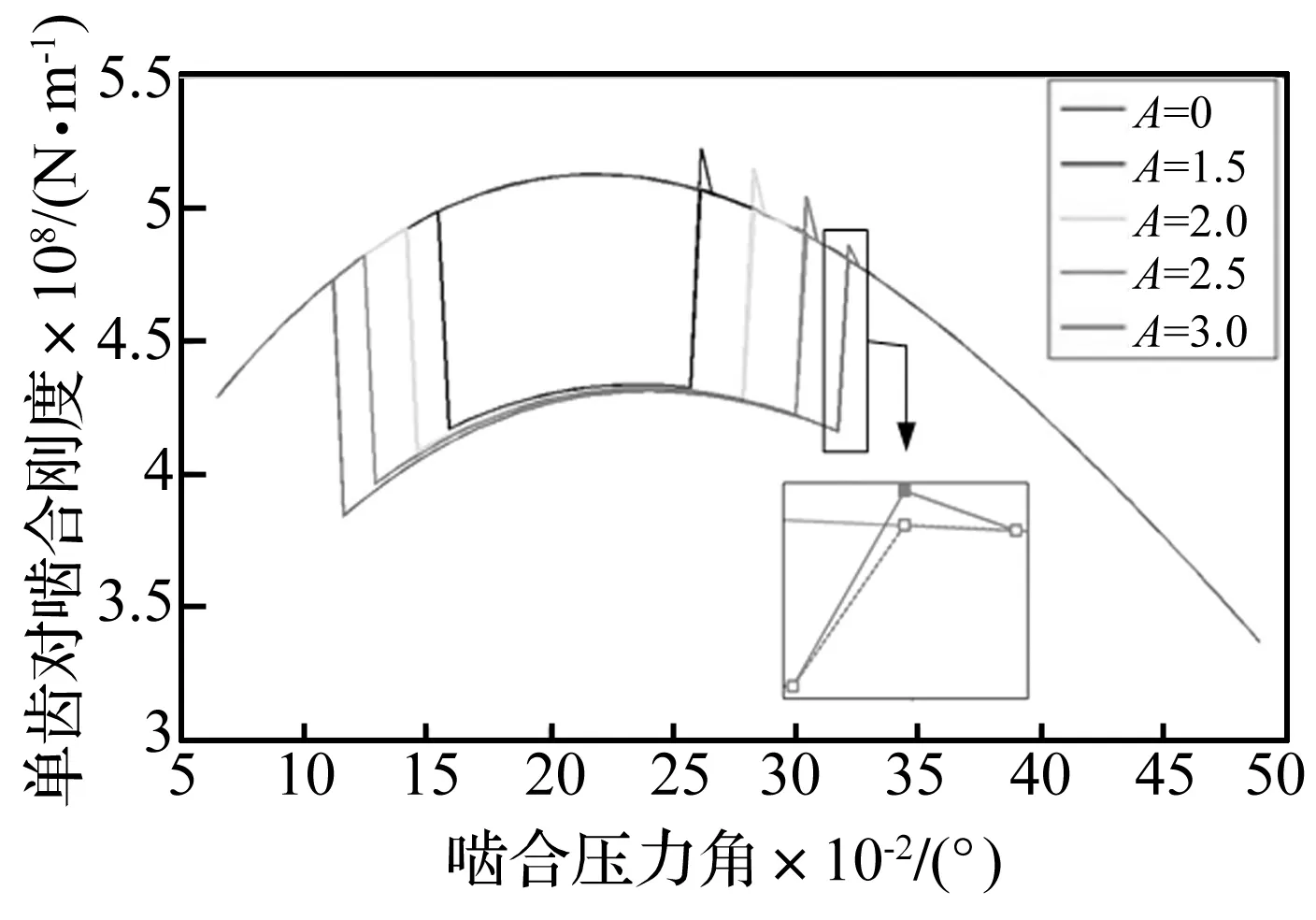
圖6 不同剝落寬度影響的單齒對嚙合剛度曲線

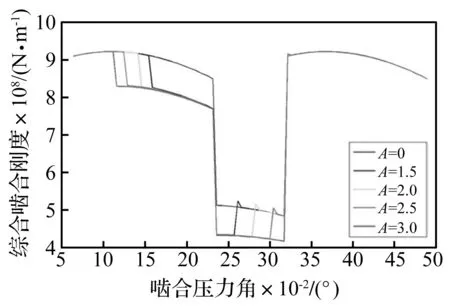
圖7 不同剝落寬度影響的綜合嚙合剛度曲線

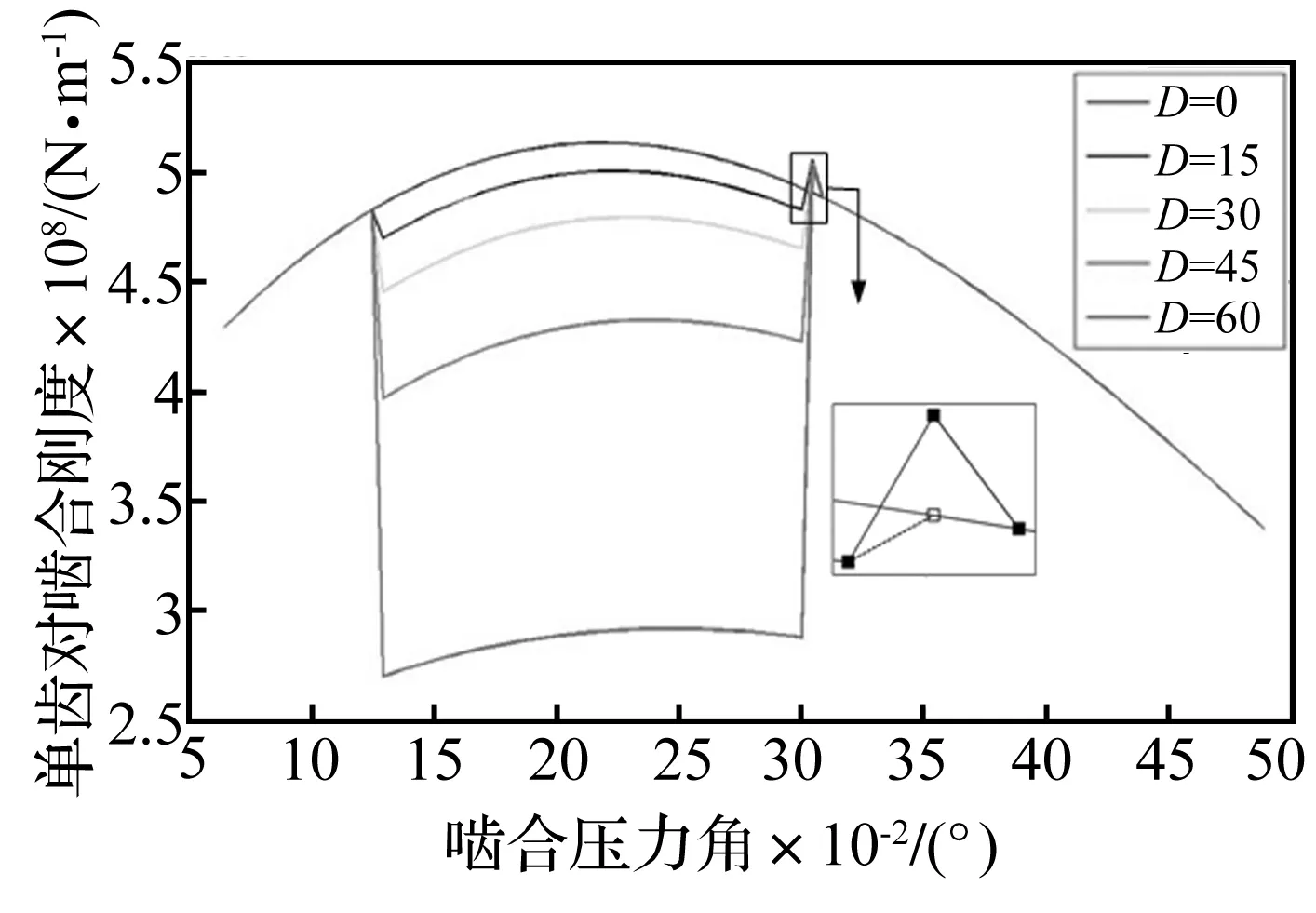
圖8 不同剝落長度影響的單齒對嚙合剛度曲線

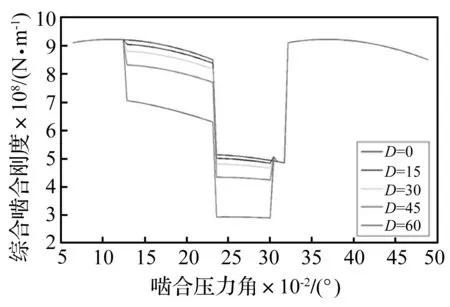
圖9 不同剝落長度影響的綜合嚙合剛度曲線

3 輪齒表面剝落缺陷的動力學響應及特征和實驗研究

3.1 齒輪系統的動力學模型

考慮邊緣接觸的剛度激勵，建立了6自由度考慮阻尼系數的直齒輪箱系統[6]，動力學模型示意圖如圖10所示。Y軸平行于輪齒嚙合線，TP/TG表示驅動/制動扭矩，ΩP/ΩG表示小齒輪/大齒輪的工作轉速，JP/JG表示小齒輪/大齒輪的轉動慣量，KiBj/CIBj表示支撐軸承的剛度和阻尼，i分別表示小齒輪和大齒輪，j分別表示x和y坐標軸方向，mP/mG表示小齒輪和大齒輪質量，K(t)表示時變嚙合剛度，Cm表示輪齒嚙合阻尼，Ff表示存在于嚙合輪齒間的摩擦力。

直齒輪系統的參數，如表1所示。施加到直齒輪系統的負載扭矩為60 Nm，仿真轉動頻率為10 Hz。采用Coulomp摩擦模型，其動力學摩擦系數u參考文獻[6]。

建立系統振動方程式為：

Mx″+Cx′+Kx=F

(25)

(26)

(27)

(28)

(29)

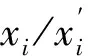
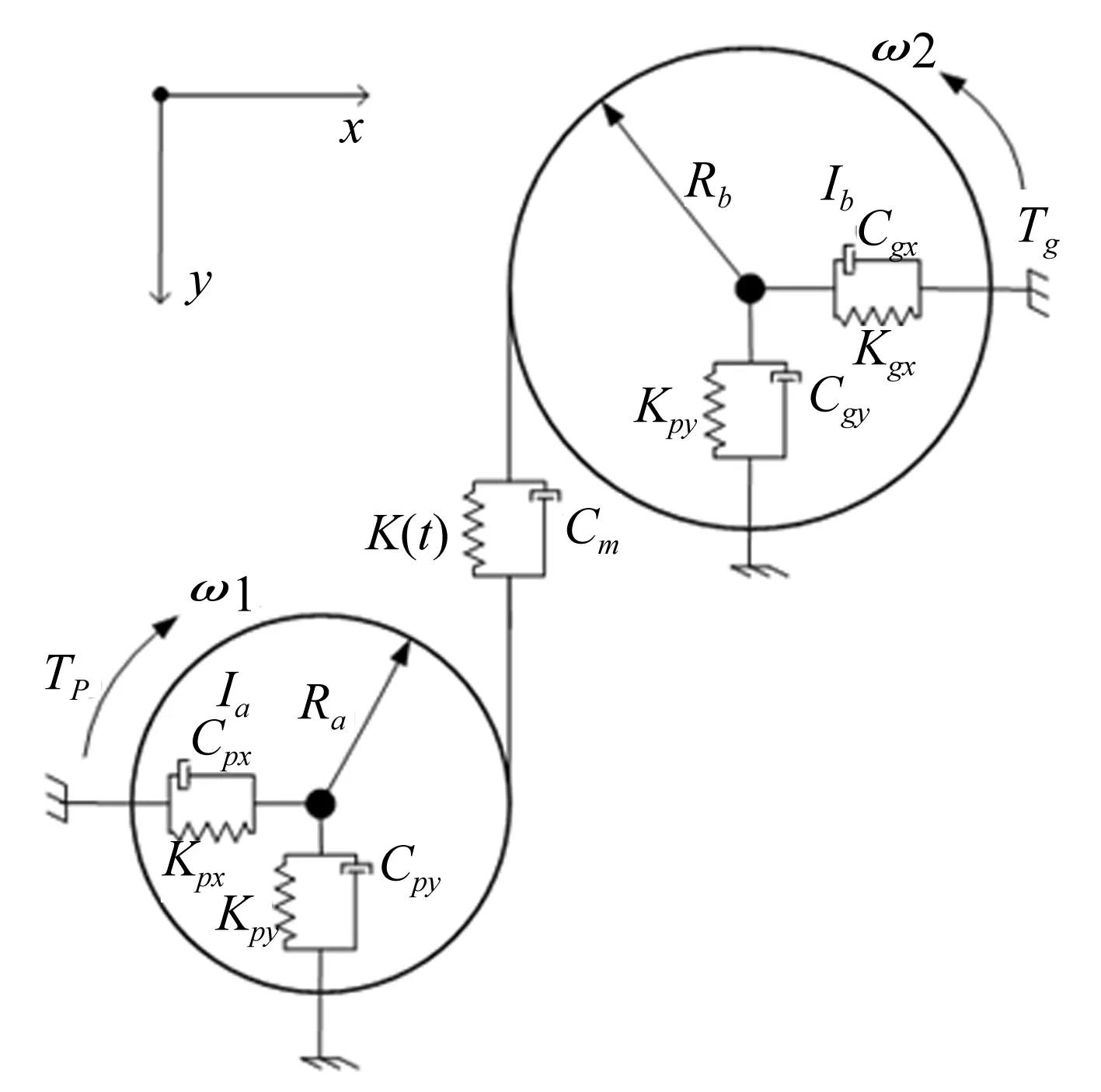
圖10 齒輪系統動力學模型

3.2 輪齒表面剝落缺陷對系統動態特性影響分析

采用龍格-庫塔法求解時變剛度激勵的動力學方程，獲得系統動態響應。

仿真計算直齒輪系統的小齒輪y向動態響應，其正常動態響應時域圖和頻譜圖，如圖11所示，其時域信號平穩，有嚙合頻率和諧頻成分。

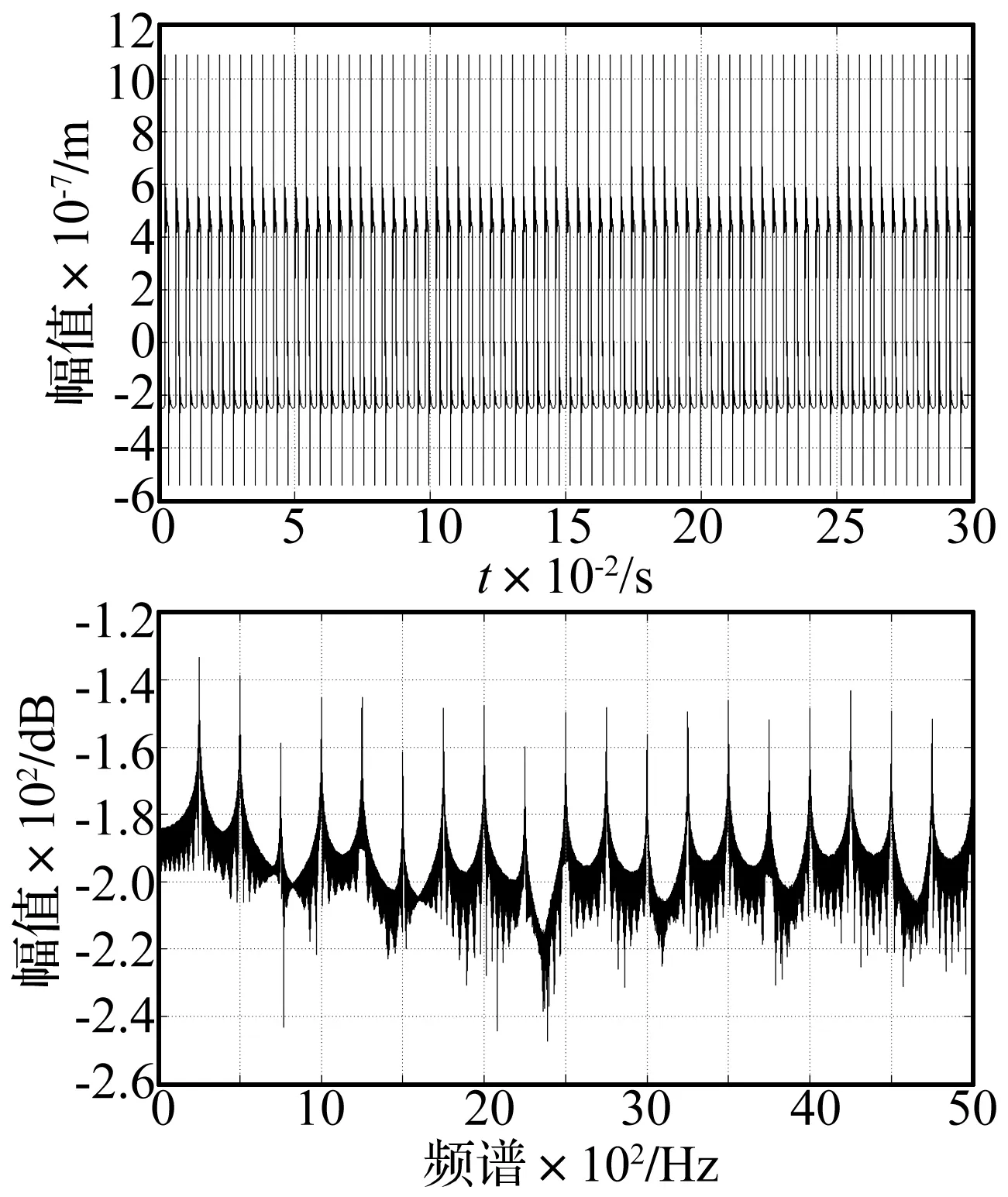
圖11 正常小齒輪y向動態響應時域圖及頻譜圖(D=0 mm,A=0 mm)

穩定狀態的剝落缺陷影響的時域圖和頻譜分別如圖12 (D=45 mm,A=2 mm)、圖13 (D=45 mm,A=3 mm) 和圖14(D=60 mm,A=2 mm)所示。紅色線、藍色線分別表示考慮邊緣接觸和不考慮邊緣接觸的響應。時域分析顯示初期剝落輪齒產生的時域信號特性并不明顯。然而，當剝落寬度和長度擴展到一定程度，出現明顯的沖擊，相鄰沖擊間的間隔時間T(0.1 s)和小齒輪轉動周期(60/600=0.1 s)相同。

包絡解調頻譜顯示剝落缺陷寬度和長度擴展，影響嚙合頻率及其諧頻以及邊頻的變化，其特點是：邊頻明顯增強，而齒輪嚙合頻率及其諧頻幅值增長相對緩慢，邊頻特征比齒輪嚙合頻率及其諧頻對于剝落缺陷擴展更加敏感，其結果與文獻[1]及文獻[3]的有限元計算結論一致，從另一個角度驗證了本研究方法的正確性。

3.3 輪齒表面剝落缺陷實驗與特性研究

為驗證理論模型仿真分析的正確性，利用二級齒輪箱開展輪齒表面剝落缺陷實驗研究。實驗條件如圖15所示：輸入軸轉速600 r/min(即轉動頻率為10 Hz)，采樣頻率為10 kHz；齒面剝落缺陷設置在第二級小齒輪輪齒上，測點布置在第二級小齒輪軸承座上；齒面剝落：小缺陷(D=45 mm，A=2 mm,H=1 mm)和大缺陷(D=60 mm，A=2 mm,H=1 mm)。

齒面剝落小缺陷與大缺陷對應的振動信號時域圖和頻譜分別如圖15、圖16所示。結果表明，齒面剝落缺陷較小時，齒輪系統振動沖擊信號特征不明顯。齒面剝落缺陷越大，齒輪系統振動沖擊越明顯，如圖16所示，相鄰振動沖擊間的間隔時間T(0.101 7 s)與小齒輪轉動周期(1/9.83 s)相同。

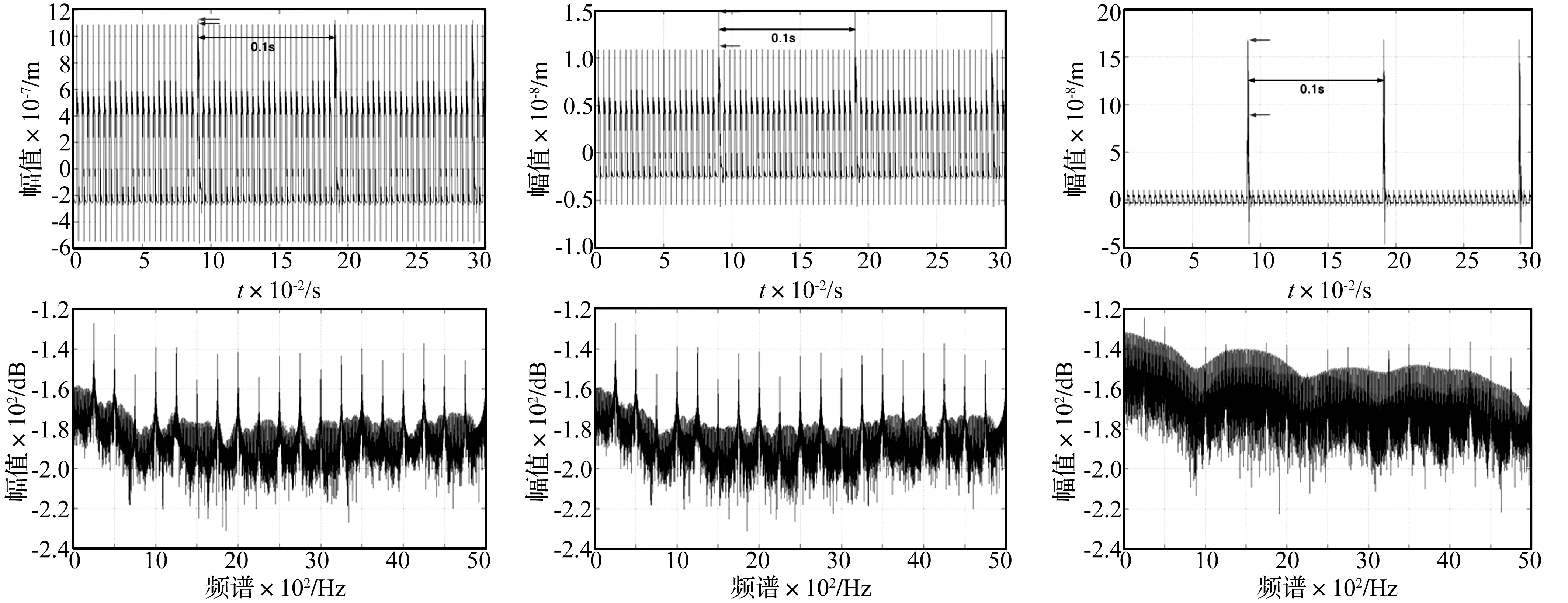
圖12 小齒輪y向動態響應時域圖、頻譜圖(D=45 mm,A=2 mm)

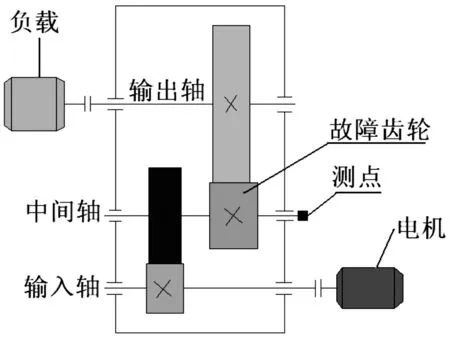
圖15 輪齒表面剝落故障實驗布置圖

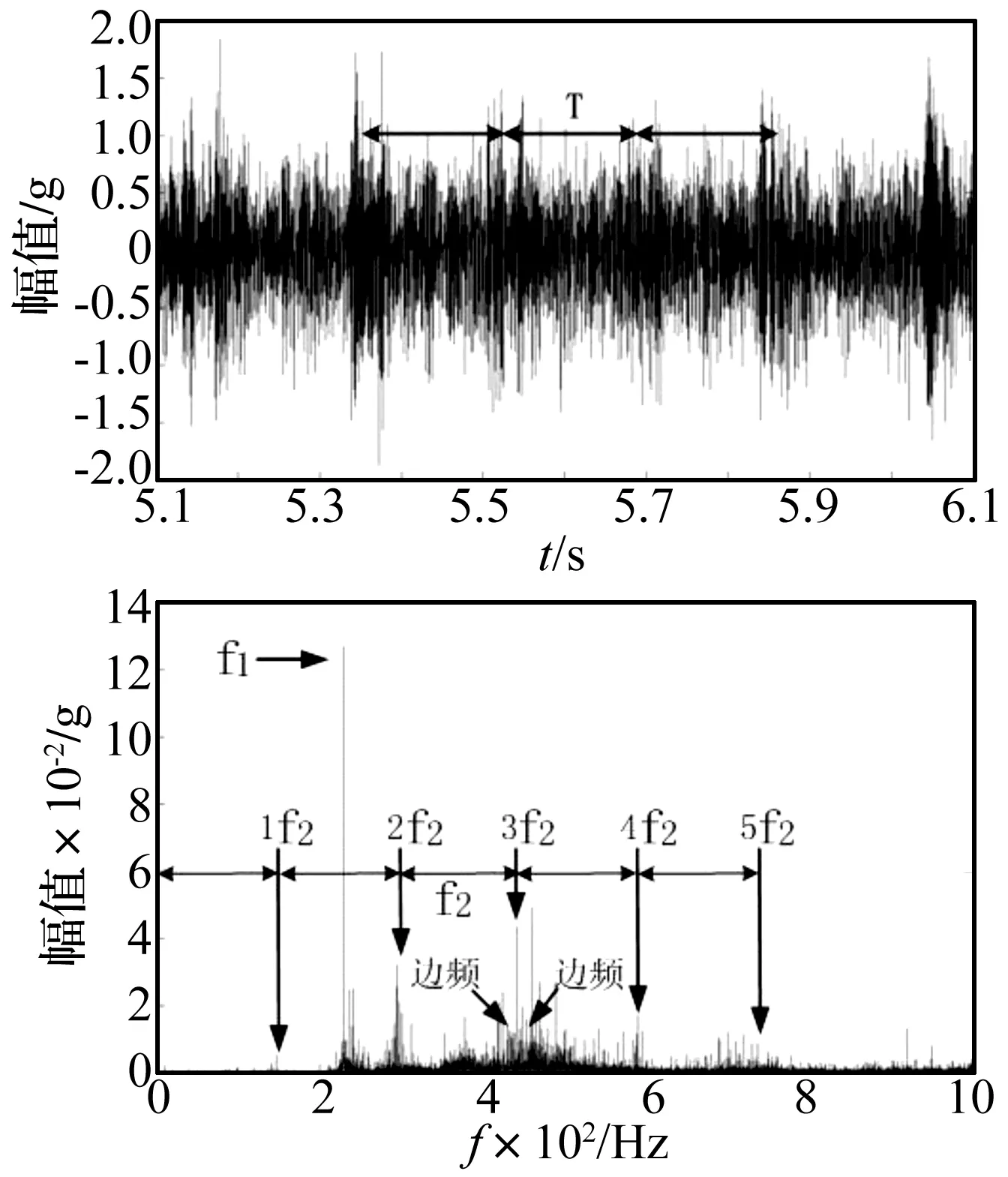
圖16 小齒輪y向實驗動態響應時域圖、頻譜圖(D=45 mm,A=2 mm,H=1 mm)

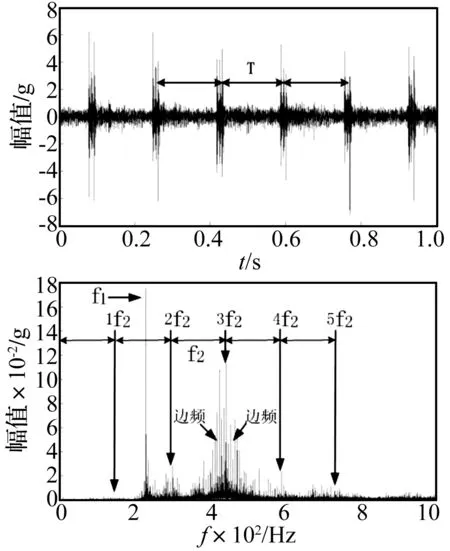
圖17 小齒輪y向實驗動態響應時域圖、頻譜圖(D=60 mm,A=2 mm,H=1 mm)

頻譜中f1表示第一級嚙合頻率(230 Hz)，f2表示第二級(缺陷齒輪)嚙合頻率(147.5 Hz)，含故障的齒輪軸轉頻為5.9 Hz；頻譜顯示，隨著剝落擴展，邊頻(與缺陷齒輪轉頻倍數吻合)明顯增強，而缺陷齒輪嚙合頻率及其諧頻幅值增長相對緩慢，邊頻特性相比齒輪嚙合頻率及其諧頻對剝落缺陷擴展更加敏感。實驗結果和文中3.2節的仿真結果吻合良好，驗證了建立的齒輪剝落缺陷動力學理論模型的正確性。

4 結 論

提出了齒面剝落復合接觸剛度模型，結合勢能原理推導了齒輪副嚙合剛度算法，分析了邊緣接觸對時變剛度激勵以及系統動態響應特性的影響，開展了輪齒表面剝落缺陷實驗研究。仿真與實驗結果表明：缺陷邊緣接觸導致嚙合剛度發生突變，其動態響應信號的嚙合頻率及其倍頻的調制邊頻成分明顯。本文提出的復合剛度模型能夠準確表征剝落缺陷嚙合的動態響應特征，可為在線監測和齒輪故障診斷提供理論支撐。

[1]Chaari F, Baccar W, Abbes M S, Mohamed Haddar, Effect of spalling or tooth breakage on gearmesh stiffness and dynamic response of a one-stage spur gear transmission, European Journal of Mechanics A/Solids,2008,27:691-705.

[2]Wu S Y, Zuo M J, Parey A, Simulation of spur gear dynamics and estimation of fault growth[J].Journal of Sound and Vibration, 2008,317:608-624.

[3]Jia S X, Howard I, Comparison of localised spalling and crack damage from dynamic modelling of spur gear vibrations[J]. Mechanical Systems and Signal Processing,2006,20:332-349.

[4]Xiao H F, Brennan M J, Shao Y M，On the undamped free vibration of a mass interacting with a Hertzian contact stiffness[J].Mechanics Research Communications，2011,38:560-564.

[5]Ding Chang-an, Zhang Lei, Zhou Fu-zhang, et al. Theoretical formula for calculation of line-contact Elastic Contact deformation[J]. Tribology，2001.

[6]Chen Z G, Shao Y M, Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth[J]. Engineering Failure Analysis, 2011.07.006.

[7]Sainsot P, Velex P, Contribution of gear body to tooth deflections-A new bidimensional analytical formula[J]. ASME J. Mec. Des.,2004,126:748-752.SHOCK,2012,31:83-89.

[8]Chen Z G, Shao Y M, Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack[J]. Mechanism and Machine Theory, 2013,62:63-74.

[9]Yang D C H, Su Z S, A rotary model for spur gear dynamics[J]. ASME J. Mech., Trans. Aut. Des.,1985,107:529-535.