Hom-結合超代數的表示和上同調
南 基 洙, 王 春 月,2, 張 慶 成
( 1.大連理工大學 數學科學學院, 遼寧 大連 116024;2.吉林工程技術師范學院 應用理學院, 吉林 長春 130052;3.東北師范大學 數學與統計學院, 吉林 長春 130024 )
?
Hom-結合超代數的表示和上同調
南 基 洙1, 王 春 月1,2, 張 慶 成*3
( 1.大連理工大學 數學科學學院, 遼寧 大連 116024;2.吉林工程技術師范學院 應用理學院, 吉林 長春 130052;3.東北師范大學 數學與統計學院, 吉林 長春 130024 )
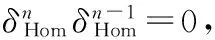
Hom-結合超代數;表示;上同調
0 引 言
結合超代數對很多代數結構研究都具有重要的作用.研究者對結合超代數的研究越來越感興趣.Ayadi等研究了具有非退化、超對稱、不變雙線性型結合超代數的結構和雙擴張[1].Montaner給出了結合超代數的理想與Lie超代數的理想之間的關系[2].Laliena等研究了具有超對合的結合超代數結構與具有反對稱元素的Lie代數結構之間的關系[3].
Hom-代數結構首先出現在Lie代數擬形變中.近年來,關于Hom-代數結構已經涌現了很多研究結果[4-7].Ammar等給出了Hom-結合代數的上同調群[8].Makhlouf等研究了Hom-結合代數的低階上同調群[9].而Ammar等在研究Hom-Lie超代數和Hom-Lie可許超代數的結構時提出了Hom-結合超代數的定義[10],它對研究Hom-Lie超代數起著重要的作用.對于Hom-結合超代數還有許多問題值得研究.本文將Hom-結合代數的上同調群推廣到Hom-結合超代數,主要研究Hom-結合超代數的表示和上同調.
1 基本概念
首先研究Hom-結合超代數的一些基本性質,給出Hom-結合超代數表示的定義.
本文中所有的超線性空間和超代數都是復數域上的超線性空間和超代數,齊次元素x的次數記為|x|.
定義1[2]設A是一個超線性空間,°:A×A→A是一個偶雙線性映射,φ:A→A是一個偶線性映射.對任意的x,y,z∈A,滿足
(x°y)°φ(z)=φ(x)°(y°z)
則稱(A,°,φ)是一個Hom-結合超代數.
設(A1,°1,φ1)和(A2,°2,φ2)是兩個Hom-結合超代數,f:A1→A2是一個偶線性映射.若f滿足
f(x°1y)=f(x)°2f(y),fφ1=φ2f
稱偶線性映射f是一個Hom-結合超代數的同態.
注當φ=id時,Hom-結合超代數是結合超代數.若偶線性映射φ:A→A滿足φ(x°y)=φ(x)°φ(y),則稱(A,°,φ)是一個保運算的Hom-結合超代數.
下面定理給出了由一個結合超代數和一個偶的結合超代數自同態構造一個Hom-結合超代數的方法.
定理1設(A,°)是一個結合超代數,φ:A→A是一個偶的結合超代數自同態,任取x,y∈A,定義運算x°φy=φ(x°y),則(A,°φ,φ)是一個Hom-結合超代數.
證明任取x,y,z∈A,則
(x°φy)°φφ(z)=φ2((x°y)°z)=φ2(x°(y°z))=φ(x)°φ(y°φz)
因此(A,°φ,φ)是一個Hom-結合超代數.
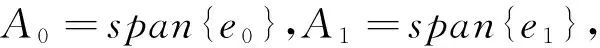
e0°e0=k1e0,e0°e1=k1e1,
e1°e0=k1e1,e1°e1=k2e0;k1,k2≠0
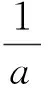
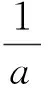
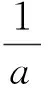
然而(A,°φ)不是一個結合超代數.事實上,當a≠±1時,
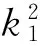
(e0°φe1)°φe1=k1k2e0≠e0°φ(e1°φe1)=a2k1k2e0;
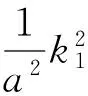
(e1°φe1)°φe0=a2k1k2e0≠e1°φ(e1°φe0)=k1k2e0
命題1設(A1,°1,φ1)和(A2,°2,φ2)是兩個Hom-結合超代數,對任意a1,a2∈A1,b1,b2∈A2,定義一個偶雙線性映射:
°:(A⊕B)×(A⊕B)→(A⊕B)
(a1+b1)°(a2+b2)=a1°1a2+b1°2b2
對任意a∈A1,b∈A2,定義一個偶映射
(φ1+φ2):A1⊕A2→A1⊕A2
(φ1+φ2)(a+b)=φ1(a)+φ2(b)
則(A1⊕A2,°,φ1+φ2)是一個Hom-結合超代數.
證明顯然A1⊕A2是一個超線性空間,φ1+φ2是一個偶線性映射.任取a1,a2,a3∈A1,b1,b2,b3∈A2,由(A1,°1,φ1)和(A2,°2,φ2)是兩個Hom-結合超代數,則有
((a1+b1)°(a2+b2))°((φ1+φ2)(a3+b3))=(a1°1a2)°1φ1(a3)+(b1°2b2)°2φ2(b3)=φ1(a1)°1(a2°1a3)+φ2(b1)°2(b2°2b3)=((φ1+φ2)(a1+b1))°((a2+b2)°(a3+b3))
因此(A1⊕A2,°,φ1+φ2)是一個Hom-結合超代數.
定義2設(A,°,φA)是一個Hom-結合超代數,V是一個超線性空間,φV:V→V是V的一個偶線性映射.在V上定義線性運算·:A×V→V,(x,v)x·v,使得下列條件成立:任取x,y∈A,v∈V,
(1)x·v∈Vθ+μ, ?x∈Aθ,?v∈Vμ;
(2)φV(x·v)=φA(x)·φV(v);
(3)(x°y)·φV(v)=φA(x)·(y·v)稱(V,·,φV) 是一個Hom-左A-模.
同樣可以定義Hom-右A-模.
定義3設(A,°,φA)是一個Hom-結合超代數,V是一個超線性空間,φV:V→V是V的一個偶線性映射.在V上定義線性運算·:V×A→V,(v,x)v·x,使得下列條件成立:任取x,y∈A,v∈V,
(1)v·x∈Vθ+μ,?x∈Aθ,?v∈Vμ;
(2)φV(v·x)=φV(v)·φA(x);
稱(V,·,φV)是一個Hom-右A-模.
若(V,·,φV)既是一個Hom-左A-模又是一個Hom-右A-模,且滿足
φA(x)·(v·y)=(x·v)·φA(y)
則稱(V,·,φV)是一個Hom-A-雙模.
例2(A,°,φA)是一個Hom-A-雙模.
例3設A是一個結合超代數,(V,·)是一個A-雙模,則(V,·)也是一個Hom-A-雙模.事實上,相當于φV=idV.
定義4設(A,°,φA)是一個Hom-結合超代數,V是一個超線性空間,φV:V→V是一個偶線性映射.如果偶線性映射ρφV:A→gl(V)滿足下列條件:
(1)ρφV(φA(x))φV=φVρφV(x);
本次研究中接受放療治療的71例腫瘤患者應用CT模擬定位掃描技術均實現了準確定位靶區,且病灶區域、靶區及毗鄰組織的界限清晰,療程結束后復查CT,并判定療效,結果顯示符合完全緩解的有26例,占36.62%,符合部分緩解的有42例,占59.15%,總有效率達到了95.77%,但仍有2例穩定,1例進展。患者放療期間均未見嚴重不良反應及并發癥。
(2)ρφV(x°y)φV=ρφV(φA(x))ρφV(y)
則稱ρφV是關于φV的(A,°,φA)在V上的一個表示.
如果定義ρφV(x)(v)=x·v(或ρφV(x)(v)=(-1)|x||v|v·x),則Hom-左(右)A-模(V,φV)與表示ρφV一一對應.
命題2設(A1,°1,φ1)和(A2,°2,φ2)是兩個Hom-結合超代數,φ:A2→A1是一個偶的Hom-結合超代數的同態,(V,·,φV)是任意一個Hom-A1-雙模.任取a2∈A2,v∈V,定義
a2·′v=φ(a2)·v,v·′a2=v·φ(a2)
則(V,·′,φV)是一個Hom-A2-雙模.
證明任取v∈V,a2,b2∈A2,則有
φV(a2·′v)=φV(φ(a2)·v)=φ1(φ(a2))·φV(v)=φ(φ2(a2))·φV(v)=φ2(a2)·′φV(v);
(a2°2b2)·′φV(v)=φ(a2°2b2)·φV(v)=(φ(a2)°1φ(b2))·φV(v)=φ2(a2)·′(b2·′v)
因此(V,·′,φV)是一個Hom-左A2-模.
同理可證(V,·′,φV)是一個Hom-右A2-模.
又因為
φ2(a2)·′(v·′b2)=φ(φ2(a2))·(v·φ(b2))=φ1(φ(a2))·(v·φ(b2))=(φ(a2)·v)·φ1(φ(b2))=(φ(a2)·v)·φ(φ2(b2))=(a2·′v)·′φ2(b2)
所以(V,·′,φV)是一個Hom-A2-雙模.
2 Hom-結合超代數的上同調
下面將給出Hom-結合超代數上同調的定義.本章中所有的Hom-結合超代數都是保運算的Hom-結合超代數.對所有齊次元素(a1,a2,…,an)∈An,記
|(a1,a2,…,an)|=|a1|+|a2|+…+|an|
定義5設(A,°,φA)是一個Hom-結合超代數,(V,·,φV)是一個Hom-A-雙模.如果齊次n-線性映射f:?nA→V滿足
(1)f(a1,a2,…,an)∈Vα,其中|f|+|a1|+|a2|+…+|an|=α;
(2)f(a1,a2,…,ai,ai+1,…,an)=-(-1)|ai||ai+1|f(a1,a2,…,ai+1,ai,…,an);
(3)φV(f(a1,a2,…,an))=f(φA(a1),φA(a2),…,φA(an))
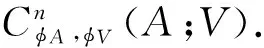
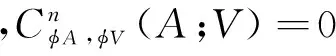
定義6設(A,°,φA)是一個Hom-結合超代數,(V,·,φV)是一個Hom-A-雙模.定義一個偶線性映射
為
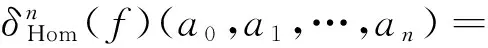
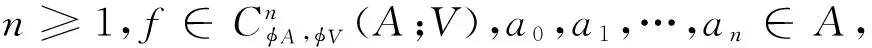
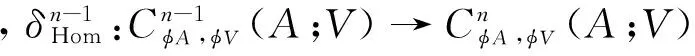
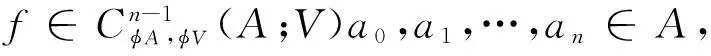
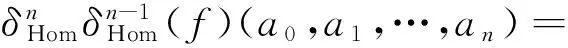
定義7
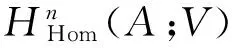
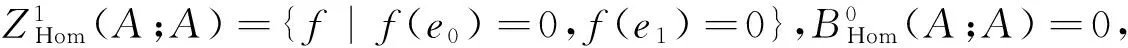
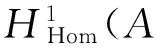
3 結 語
本文給出了Hom-結合超代數的表示和雙模的定義,并以此研究了Hom-結合超代數的上同調.
[1] Ayadi I, Benayadi S. Associative superalgebras with homogeneous symmetric structures [J].CommunicationinAlgebra, 2012,40(4):1234-1259.
[2] Montaner F. On the Lie structure of associative superalgebras [J].CommunicationinAlgebra, 1998,26(7):2337-2349.
[3] Laliena J, Sacristan S. On certain semiprime associative superalgebras [J].CommunicationinAlgebra, 2009,37(10):3548-3552.
[4] Makhlouf A, Silvestrov S. Hom-algebra structure [J].JournalofGeneralizedLieTheoryandApplications, 2008,2(2):51-64.
[5] SHENG Yun-he. Representations of Hom-Lie algebras [J].AlgebrasandRepresentationTheory, 2012,15(6):1081-1098.
[6] Yau D. Hom-algebras and homology [J].JournalofLieTheory, 2009,19(2):409-421.
[7] Yau D. Enveloping algebras of Hom-Lie algebras [J].JournalofGeneralizedLieTheoryandApplications, 2008,2(2):95-108.
[8] Ammar F, Ejbehi Z, Makhlouf A. Cohomology and deformations of Hom-algebras [J].JournalofLieTheory, 2011,21(4):813-836.
[9] Makhlouf A, Silvestrov S. Notes on formal deformations of Hom-associative and Hom-Lie algebra [EB/OL]. (2007-12-19) [2013-12-15]. http://arXiv.org/abs/0712.3130v1.
[10] Ammar F, Makhlouf A. Hom-Lie superalgebras and Hom-Lie admissible superalgebras [J].JournalofAlgebra, 2010,324(7):1513-1528.
RepresentationandcohomologyofHom-associativesuperalgebras
NAN Ji-zhu1, WANG Chun-yue1,2, ZHANG Qing-cheng*3
( 1.School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China;2.School of Applied Sciences, Jilin Teachers′ Institute of Engineering and Technology, Changchun 130052, China;3.School of Mathematics and Statistics, Northeast Normal University, Changchun 130024, China )
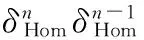
Hom-associative superalgebras; representation; cohomology
1000-8608(2014)06-0702-05
2014-01-04;
: 2014-08-04.
高等學校博士學科點專項科研基金資助項目(201101647);吉林省自然科學基金資助項目(20130101068).
南基洙(1965-),男,教授,E-mail:jznan@163.com;王春月(1979-),女,博士生,E-mail:wang1chun2yue3@163.com;張慶成*(1960-),男,教授,E-mail:zhangqc569@nenu.edu.cn.
O152.5
:Adoi:10.7511/dllgxb201406016

