熱光二階關聯的影響因素實驗研究

田 甲，林海龍，高 祿

(中國地質大學(北京) 數理學院，北京 100083)

1 引 言

1956年，漢勃雷-布朗(R. H. Brown)和特威斯(R. Q. Twiss)為測量恒星角直徑而設計著名的實驗[1]，后來人們就以他們的名字命名該實驗為“HBT”實驗. HBT實驗第一次證實了光的強度關聯效應, 實驗本身也成為測量強度關聯的典型方法,在量子光學發展史上具有里程碑的意義. 1995年,美國馬里蘭大學的Yanhua Shih等人利用自發參量下轉換的糾纏光子對完成了奇特的成像實驗——鬼成像(ghost imaging)[2],此實驗使得在沒有物體的閑散光路中獲得物體的空間信息成為了可能. 當時人們認為這是一種量子現象,只有采用糾纏雙光源才能實現鬼成像. 2002年, Rochester大學的Boyd等人巧妙地利用隨機旋轉的反射鏡反射激光獲得了空間頻率隨機分布的熱光源,通過光場的強度測量獲得了透射物體的鬼成像[3]. 該實驗結果表明鬼成像實驗也可以利用經典光源實現，而并非是量子光源所特有的現象. 這一實驗報道更是引起了科學界的一場爭辯：鬼成像實驗是否是一種量子現象？ 隨后，國內外很多研究組在熱光二階關聯測量方面開展了理論和實驗研究工作[4-7]. 研究結果表明熱光源可以模仿糾纏雙光子源實現鬼干涉、鬼成像等雙光子關聯測量實驗.

在研究熱光二階關聯特性的實驗中，HBT測量是一個必要的實驗基礎，因此對于HBT影響因素的研究極為關鍵. 本實驗中，采用激光照射旋轉毛玻璃形成空間頻率隨機分布的熱光源，通過改變熱光源的橫向尺寸及物光和參考光光程差，研究光源特性及光路設計對熱光二階關聯的影響.

2 實驗原理

HBT的實驗原理如圖1所示. 非相干熱光源發出的光被非偏振分束器分成2束，分別自由傳遞到達探測器D1和D2. 將其中一個探測器探測面上某一固定點的光強值與另一個探測器探測面上各個點的光強值進行強度關聯測量，即可獲得HBT值.

圖1 HBT實驗原理圖

根據高斯矩定理,滿足高斯統計分布光場的高階關聯可以用一階關聯函數表示，則熱光場的二階關聯函數可以表示為

(1)

光場從光源橫截面到探測器的探測面自由傳播的脈沖響應函數可以表示為

(2)

其中k=2π/λ為光場的波數，z是從光源橫截面到探測器的探測面的距離，xj和x0分別表示探測面和光源橫截面的空間橫向坐標. 在近軸近似條件下，式(2)可以寫為

(3)

假設理想情況下，熱光源發出的光具有無窮小的相干長度，熱光源橫截面的一階關聯函數可以表示為

〈E0(x)E0(x′)〉=S0δ(x0-x0′) ,

(4)

這里假設光場強度分布為常量S0. 將式(3)和(4)代入到式(1)中的關聯項，可以得到光場的一階互關聯函數為

(5)

其中r為光源發光面的尺寸半徑. 于是，可以得到HBT實驗的二階關聯函數為

(6)

固定一個探測器，掃描另一個探測器就可以得到

(7)

式(7)表示非相干熱光源HBT實驗測得的二階關聯函數形式，其歸一化形式可以表示為

(8)

從式(8)中可以看到，歸一化HBT曲線的半高寬與光源距探測面的距離z、光源的尺寸r及波長λ有關. HBT曲線的半高寬隨著z的增加而增大，隨r的增加而減小. HBT理論曲線如圖2所示.

圖2 HBT理論曲線圖

3 實驗研究

3.1 實驗裝置

實驗光路如圖3所示. 波長為632.8 nm的激光器發出的激光經過平面鏡M反射，依次通過偏振片P1和P2，它們的作用是保證光源為線偏振光，同時可以組合調節光強. 擴束透鏡N可以調整激光光斑的大小. 經擴束后的激光照射在轉動的毛玻璃G上形成空間頻率隨機分布的贗熱光源. P3為放置在熱光源附近的光闌，用來調節熱光源的橫向尺寸. BS為50/50非偏振分束器，可以把光源發出的光束分為2束，2束光分別自由傳遞到達探測器D1和D2的探測面. 兩探測器的探測面距離熱光源G的距離分別為d1和d2. 2個探測器分別連接計算機中采集卡的端口，由相應的采集程序進行數據采集和測量，并將數據存儲到計算機中.

圖3 HBT實驗裝置圖

依據HBT原理，本實驗所采用的采集方式為：取探測器D1探測面上某一固定點值與另一個探測器D2探測面上的各個點的光強值進行關聯測量，對采集到的數據進行歸一化關聯計算，從而得到光場的二階關聯HBT值.

3.2 實驗過程及結果

首先,固定光闌P3的直徑為3 mm，通過改變探測器D2距離光源的光程，改變物光和參考光兩光路的光程差，測量相應的HBT值. 探測器D1保持位置不變，距離分束器BS的距離為d1=31.80 cm,探測器D2的位置依次變化使光程差分別為Δd=d2-d1=0,5,10,20 cm. 實驗結果如圖4所示. 當Δd=0 cm時，歸一化的HBT值達到了1.935，接近理想值2;隨著探測器到光源光程差的增加，HBT值逐漸減小. 當光程差Δd達到20 cm時，二階關聯的HBT值減到1.221，二階關聯值變得較低. 實驗結果表明：熱光二階關聯隨著2個光路光程差的增大而下降，同時曲線的半高寬也隨之增大，導致二階關聯測量的分辨率降低. 所以在上述熱光二階關聯實驗測量系統中，在光源尺寸是直徑為1 mm的圓形區域情況下，物光和參考光兩光路的光程差不能大于20 cm,否則二階關聯特性將消失.

圖4 HBT值隨光程差變化曲線

其次，固定探測器D1和D2的位置，即d1=d2=31.80 cm. 通過改變光闌P3的直徑即熱光源的橫向尺寸，測量相應的HBT值. 實驗測量結果如圖5所示. 實驗結果表明：當光闌直徑為1 mm時，關聯值達到1.797；隨著光闌直徑的增大，HBT值逐漸減小，當直徑增加到10 mm時，二階關聯值下降到1.361. 由此可見，強度關聯值隨著熱光源橫截面尺寸的增大而降低. 同時，HBT曲線的半高全寬隨著光闌直徑的增加而減小，這說明熱光二階關聯測量系統的分辨率隨著光闌直徑的增加而提高.

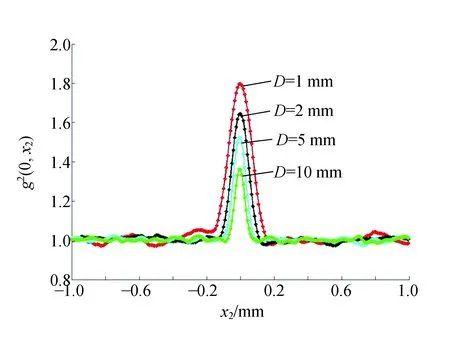
圖5 HBT值隨光闌直徑變化曲線

4 結 論

熱光的歸一化二階關聯HBT值與物光和參考光光程差及光源的橫截面尺寸有緊密聯系. 研究結果表明：隨著熱光二階關聯測量系統中物光和參考光光程差增加，HBT值會隨之降低，而且曲線的半高全寬也隨之增加，導致系統的測量分辨率降低. 隨著光源橫截面尺寸增加，即實驗裝置中光闌P3直徑增大，HBT值也會隨之降低，但是曲線的半高全寬卻隨之減小，系統的測量分辨率提高. 這說明盡管光源橫截面尺寸的增加可以提高熱光關聯系統的測量分辨率，但是要以降低圖像可見度為代價.

參考文獻：

[1] Brown R H, Twiss R Q. Correlation between photons in two coherent beams of light [J]. Nature, 1956,177:27-29.

[2] Pittman T B, Shih Y H, Strekalov D V, et al. Optical imaging by means of two-photon quantum entanglemen [J]. Phys. Rev. A, 1995,52:R3429-R3432.

[3] Bennink R S, Bentley S J, Boyd R W. “Two-photon” coincidence imaging with aclassical source [J]. Phys. Rev. Lett., 2002,89(11):113601-1-4.

[4] Cao De-zhong, Wang Kai-ge. Sub-wavelength Interference in macroscopic observation [J]. Phys. Lett. A, 2004,333:23-29.

[5] GAO Lu, XIONG Jun, ZHANG Shu-heng, et al. Improving visibility of diffraction pattern with pseudo-thermal light [J]. Chin. Phus. Lett. , 2008,25(4):1277.

[6] 李璐，關東石，劉宏超，等. 光的偏振性對Hanbury Browm-Twiss實驗的影響[J]. 量子光學學報，2009(3):201-206.

[7] 高祿，張穎濤，汪凱戈. 相位物體的熱光關聯成像[A]. 第十二屆全國量子光學學術會議論文集[C]. 南昌：2006.