飛機液壓助力器模型分析

周華剛，曹春泉，余慧玲

(中航通飛研究院有限公司系統研究室，廣東珠海519040)

現代大型或快速飛機由于操縱面載荷的增大，普遍采用液壓伺服作動器推動操縱面偏轉，實現飛機的姿態控制。全電傳無機械備份的飛機，采用的是電液伺服作動器，該類作動器采用的是內反饋，在考慮伺服系統設計時主要考慮系統的功率、響應速度等參數，一般不會出現系統不穩定的情況;而使用機械備份的電傳飛機和使用機械助力系統的飛機，由于使用的是外反饋的伺服作動器，也稱助力器，總是會遇到系統參數不匹配導致的系統穩定性問題。這種不穩定現象在蘇聯制米格-19，國產殲6、殲7、殲8、運8等飛機上都有出現。這種不穩定會使操縱面在助力器的推動下產生低頻自激振蕩，容易造成附件損壞、接頭松動，直接影響操縱系統的使用壽命和工作可靠性;對飛機則會影響飛行品質，嚴重時甚至影響飛機的飛行安全［1－3］。

據了解，國內設計生產的使用液壓助力器飛機，都是先安裝了助力器，在試驗中發現了不穩定才去考慮匹配的問題，導致飛機的研制周期延長、成本增加。為此，借鑒國內的研制經驗和既有成果，構建基于數字平臺的飛機操縱面伺服作動系統仿真模型，以數字仿真的方法分析影響系統穩定性的主要因素，在伺服作動器制造和裝機前完成仿真分析工作，為樣件試制和試驗提供初步條件，降低樣件設計試驗成本。

控制系統的設計，特別是工程應用時通常使用的都是線性化的模型，而助力器由于涉及到液壓油的工作問題，其工作是典型的非線性問題。因此本文作者針對此系統建立了非線性模型，并分析了線性模型的不足。

圖1是單腔室液壓助力器的原理圖［4－5］。

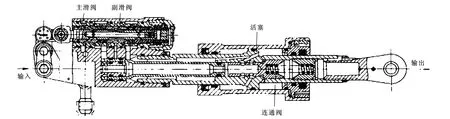
圖1 單腔式液壓助力器原理圖

1 仿真模型的建立及結果分析

1.1 常用模型

助力器由四通閥和液壓缸組成，是最常見的動力機構，其動態特性主要取決于伺服閥、液壓缸和負載，其簡化模型見圖2。在動力機構分析中，假定系統負載為質量、彈簧和黏性阻尼組成的單自由度系統［6－8］。

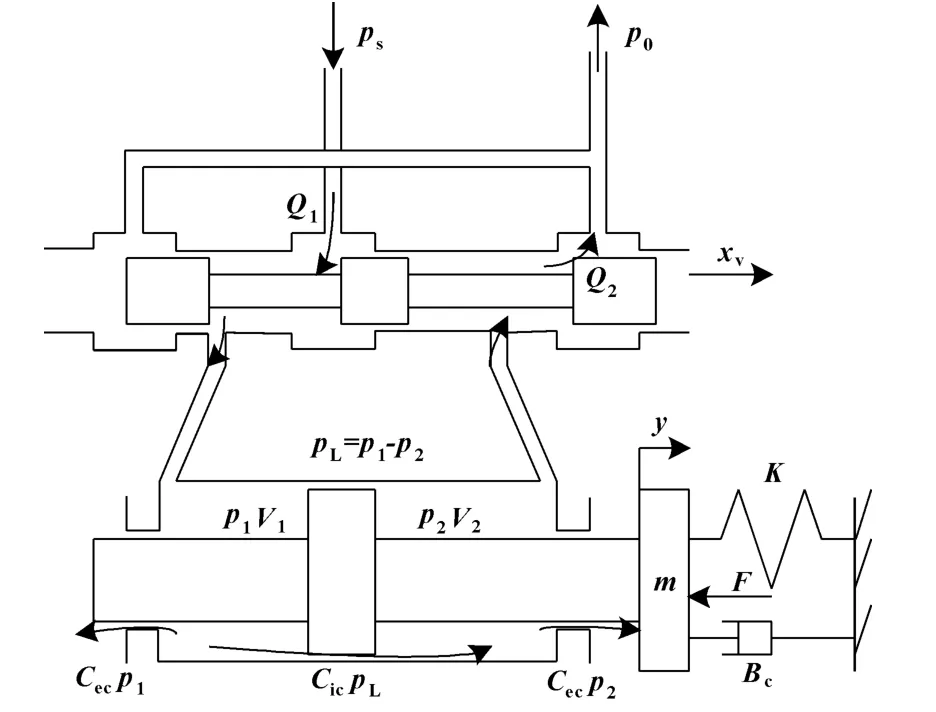
圖2 四通閥控液壓缸動力機構

滑閥運動方程

非線性方程

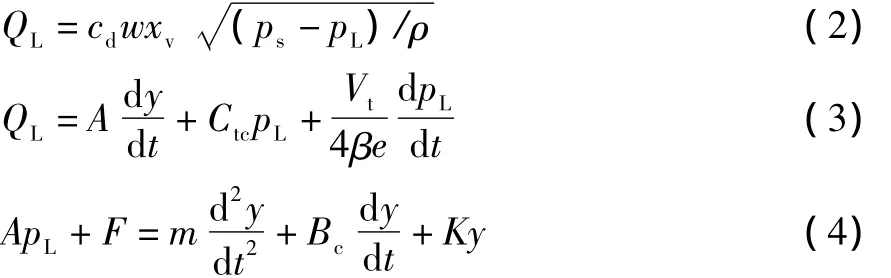
線性化方程

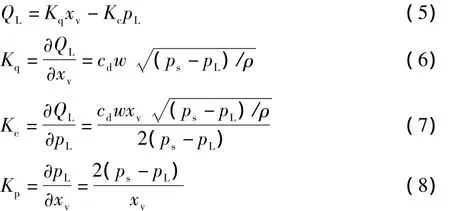
式中:Ki為輸入系數;

Kf為反饋系數;

xi為輸入信號幅值，m;

xf(Y)為輸出信號幅值，m;

cd為流量系數，通過參考資料知其值為0.61～0.62;

xv為滑閥位移，m;

w為滑閥節流窗口面積梯度。若采用整周圓開口，則w=πd，d為滑閥的直徑;

ρ為液壓油的密度，一般為850～1 200 kg/m3;

ps為液壓源的壓力;

pL為液壓缸活塞兩端壓力差;

βe為液體體積彈性模量，Pa，一般取1 225～1 372 MPa;

Kq為一般選用零位條件下的計算值 (QL=0，xv=0，pL=0);

Kc為一般使用節流孔來估算，，r是閥芯與閥套之間的徑向間隙，可取5×10－6m，μ是液體動力黏度，一般取μ=1.37×10－2Pa·s;

Ctc為總泄漏系數，(m3/s)/Pa，Ctc=Cic+Cec/2;

Vt為液壓缸的總液體體積，Vt=A×L，L是活塞的總行程;

m為活塞及負載的總質量，kg;

Bc為黏性阻尼系數，N/(m/s);

K為負載彈簧剛度，N/m;

A為活塞面積，m2;

F為負載力，N。

1.2 線性化方程的傳遞函數

線性化方程的傳遞函數由圖3求出，可推導出活塞輸出位移與滑閥位移及負載間的關系。

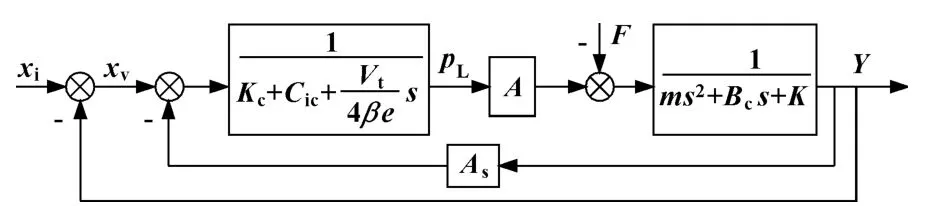
圖3 四通閥控液壓缸動力機構方框圖

利用頻域分析的方法可以判定Kf×Kq/A＜2ζhwh系統才是穩定的［9－10］。轉換為系統參數就是

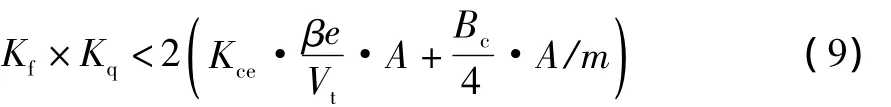
即當系統參數滿足式 (9)時，系統都能達到穩定。

當以參數Ki=0.5，Kf=0.5，F=10 000 N，Kq=0.45(m3/s)/m，Kce=1.7 × 10－11(m3/s)/Pa，A=1.25×10－3m2，m=25 kg，L=0.12 m，Vt=A × L=1.5 ×10－4m3，βe=1 250 ×106Pa，Bc=100 N/(m/s)。進行仿真時，以階躍輸入信號作為輸入時，系統的響應及部分參數見圖4。從圖中可見活塞兩端的壓力差pL達到了600 MPa，而系統的最大輸入壓力才能是20.6 MPa;系統的流量達到了1 000 L/min，這些參數使系統在階躍輸入下形成了穩定的輸出，但實際的助力系統是不能實現上述的兩個參數值的。

圖4 線性系統在階躍輸入下的響應

圖5為線性系統在多種頻率輸入下系統的響應。

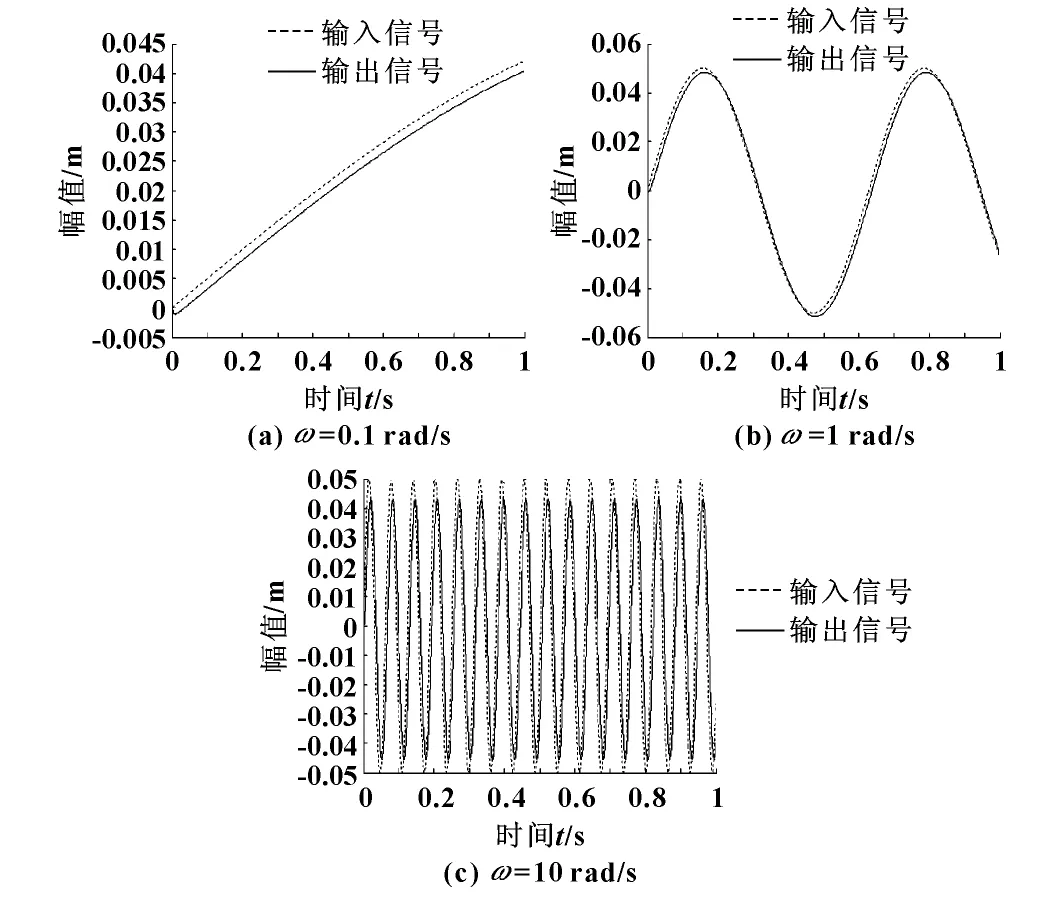
圖5 線性系統在多種頻率輸入下系統的響應

當輸入信號的頻率依次從0.1 rad/s、1 rad/s到10 rad/s時，系統都能有穩定的輸出，仿真結果見圖5。助力器－操縱面系統是一個典型的非線性系統，已經證實了助力器只有在一定頻率范圍內的輸入信號是穩定的，超出該頻率范圍的輸入都不會得到穩定的輸出［11－12］。

上述對線性化模型的仿真，從流量、壓力和頻率響應情況都說明了線性化模型并不能真實反應系統的實際運行情況;因此需要模型進行修正。

1.3 修正后的模型

式 (6)kqxv的表達式已經與流量的非線性表達式 (2)完全相同，這時線性化的方程 (5)卻還需要減去KcpL。若KcpL相對Kqxv是很小的，則可忽略不計，若不是相對很小的，則線性化的方程與非線性方程就有較大的誤差。

例如:系統為0.06 m/s的穩定輸出，需要xv=5.14×10－4m的滑閥開度，其中Kq=0.45(m3/s)/m，Kc=1.5×10－11(m3/s)/Pa，代入式 (5)，得到QL=Kqxv－KcpL≈3.07 L/min。

但同樣的滑閥開度和同樣的負載壓差，代入式(2)的流量方程為:

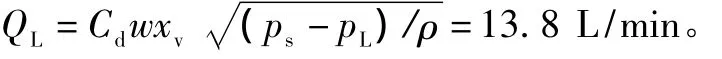
而實際系統需要流量是A˙y=8.33×10－4×0.06×6×104≈3 L/min(不考慮泄漏)。可以看到同樣的參數，非線性方程和線性化方程的流量差別很大。

為此建立助力器輸入腔和輸出腔兩者的方程，分別對兩腔的液壓參數進行仿真和分析。

滑閥流量方程:

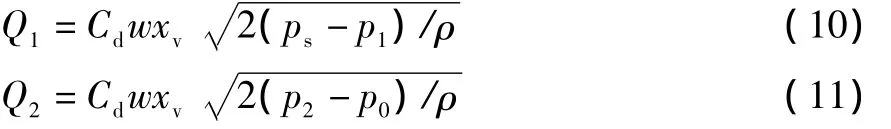
液壓缸連續性方程

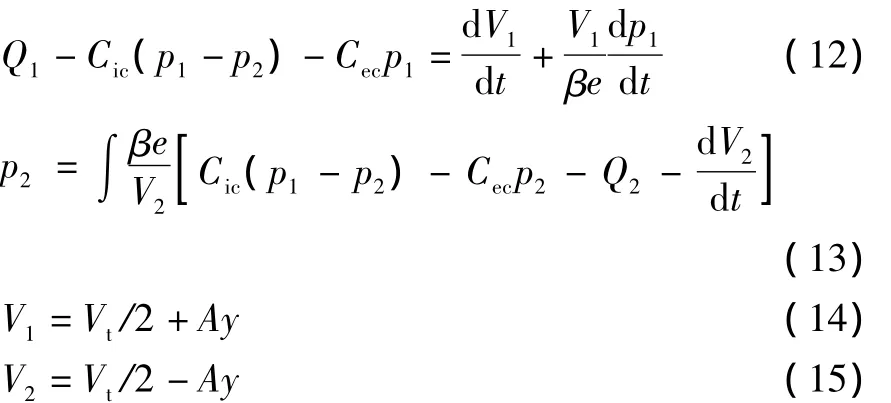
動力機構力平衡方程

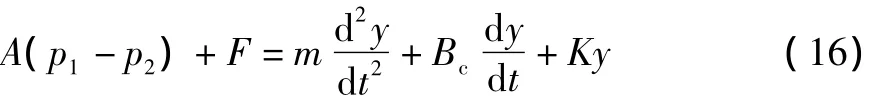
各項仿真參數為:

Cd=0.62，ps=20.6 MPa，p0=1 MPa，ρ=870 m3/s，βe=1 250 MPa，Cic=1 × 10－13(m3/s)/Pa，A=4×10－3m2，F=30 000 N，Vt=1 ×10－3m3，w=π/400 m。

圖6為非線性方程仿真結果，可以看出，系統的壓差、流量等的變化更能真實反映機構的情況，如壓差變化、流量系數、流量壓力系數等。系統速度穩定時的流量要求是24在L/min，系統的泄漏系數是Cic=1×10－13(m3/s)/Pa，在10 MPa的壓差下，流量是0.06 L/min，總流量與圖6中的流量仿真結果24.07 L/min結果一致。這種仿真模型能實時計算流量系數和流量壓力系數，圖6中的仿真結果特別是穩態值與線性化方程的穩定值要求接近。

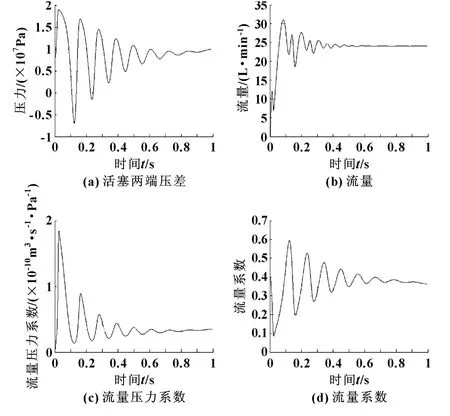
圖6 非線性方程仿真結果

2 結論

通過分別建立進回油腔的仿真模型，對其參數進行仿真更能反映系統的現實情況。現有的線性化模型在初期設計時有一定的作用，但不能真實體現助力器的工作情況，有一定的誤導。根據現有的工作經驗，只有建立全系統的非線性及彈性模型，才能真正地對助力器及系統的設計提供一定的參考。

【1】王占勇，祝華遠，唐有才．飛機液壓助力器的穩定性分析［J］．機床與液壓，2006，34(1):84 －85．

【2】陳召濤，孫秦．液壓助力器動態特性Simulink仿真與優化［J］．機械設計與制造，2006(1):96 －97．

【3】杜來林，鄭勇．影響液壓助力器穩定性的因素及改善措施［J］．液壓氣動與密封，2008(4):17 －19．

【4】吳振順．液壓控制系統［M］．北京:高等教育出版社，2008．5．

【5】王春行．液壓伺服控制系統［M］．北京:機械工業出版社，1987．

【6】郭輝，王平軍，郭濤．基于Simulink的飛機液壓助力器建模與仿真研究［J］．機床與液壓，2007，35(9):222 －223．

【7】李培滋，王占林．飛機液壓傳動與伺服控制［M］．北京:國防工業出版社，1979．

【8】林其昌，王新洲．直-9直升機主液壓助力器穩定性分析［J］．直升機技術．2000(1):32－38．

【9】楊國禎．飛機流體傳動與控制［D］．西安:空軍工程學院，1987．

【10】李永堂，雷步芳．液壓系統建模與仿真［M］．北京:冶金工業出版社，2003．

【11】Ming-Chang．The Adaptive Position Control of an Electro Hydraulic Servo Cylinder［J］．JSMME International Journal，1991(3):370－375．

【12】文韜．某型飛機空中飄擺故障分析及防護措施［J］．長沙航空職業技術學院學報，2007(2):33－35．