基于Omega理論的外嚙合齒輪泵磨損壽命分析

王曉紅，閆玉潔，李秋茜

(北京航空航天大學可靠性與系統工程學院，北京100191)

據統計，液壓系統的故障大約有80%～90%是由油液的污染引起的，其中固體顆粒污染物引起的液壓系統故障占總污染故障的60% ～70%［1］。對于齒輪泵元件，顆粒污染物使得泵的相對運動部件如齒輪端面和側板、齒輪和殼體等零件磨損加劇，使泵的流量減小、壓力降低、功率和效率也相應降低，使泵壽命縮短甚至損壞。按照傳統的液壓泵污染敏感度試驗的要求得到的是液壓泵的流量退化曲線，難以將曲線作為結果應用到實際中，因此需要將試驗結果與相應的理論進行結合，使得結果能夠定量地分析泵的抗污染性能，并反映泵的污染壽命。將Omega理論應用到泵的污染敏感度試驗中，根據外嚙合齒輪泵的磨損泄漏模型得到其流量衰減擬合公式來對試驗數據進行優化，是準確評價其抗污染磨損的性能并預測其污染磨損壽命的一種方法，將為外嚙合齒輪泵進行合理的污染控制、提高液壓系統工作效率提供重要的依據。

1 外嚙合齒輪泵的磨損泄漏模型

研究污染磨損對齒輪泵壽命的影響，可將輸出流量視為其性能下降的基本參數，液壓泵流量降低的原因主要是因磨損所導致的泄漏損失。對于側板有自動補償作用的外嚙合齒輪泵，可以認為齒輪泵內泄量僅為齒頂與殼體的間隙泄漏［2］。

根據Wilson的泵的模型［4］，泄漏量Q等于:

式中:r為齒輪半徑;ω為齒輪角速度;h為泄漏路徑的間隙;μ為油液的動態黏度;L為泄漏路徑的寬度;b為齒輪厚度;p為泵的進口和出口的壓差。

因此，流量退化比為實際流量Qa與理想流量Q0的比值:

經變換可得:

2 Omega理論

Omega理論又稱污染敏感度理論，在這個理論中污染敏感度系數Si作為一個整體參數代表元件對污染物的耐受度，它可以描述單個污染顆粒致使液壓元件產生的性能衰退。因此，在一定油液污染條件下，液壓元件的某一基本性能衰退量就等于流量與所有尺寸區間內的顆粒污染敏感度系數的乘積之和。由此可以建立液壓元件性能退化的基本方程:

式中:P為反映液壓元件基本性能的參數，dPi表示由尺寸區間i內的污染顆粒所造成的性能退化;Si為液壓元件在尺寸區間i的顆粒污染物的敏感度系數;ni為尺寸區間為i的污染顆粒濃度;“－”表示性能下降。

公式 (4)對所有液壓元件因污染顆粒所引起的性能退化均適用，對泵和伺服閥的磨損而言，可將輸出流量視為其性能下降的基本參數，對伺服閥的卡滯可以將伺服閥的死區大小作為其性能下降的基本參數，對作動筒的磨損來說可以將速度作為其性能退化的基本參數。

將流量Q作為泵性能下降的基本參數，則泵的性能退化方程為:

泵在不斷磨損的同時污染顆粒濃度逐漸降低，試驗結果表明能對元件產生磨損的污染顆粒濃度ni隨時間成指數關系變化:

式中:n0，i為尺寸區間i的顆粒污染物的初始濃度;n0，i=ni－ni+1;ni(t)為 t時間段后的污染濃度;τ為顆粒磨損時間常數，一般為顆粒濃度降低到初始濃度的37%所用的時間，大量統計分析表明，無論元件類型、元件大小還是微粒大小間隔，其磨損時間常數都被近似估計為9 min。

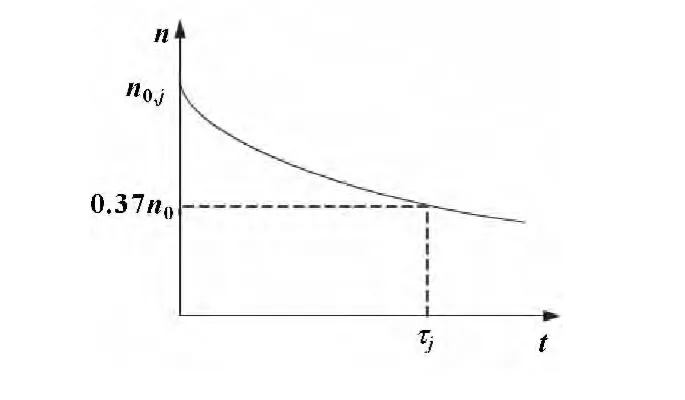
圖1 顆粒磨滅曲線

將公式 (6)代入公式 (5)可得:

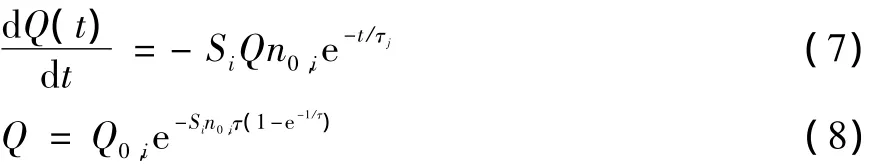
式中:Q0，i為泵的初始流量即額定流量。

當t趨近于正無窮時，泵的最終穩定流量Qf，i為:

由式 (9)可得到污染敏感度系數Si為:

式中:Qf，i為泵的實際輸出流量;Q0，i為泵的初始流量。

在上述方程的基礎上，不同尺寸區間的Si可以通過S1推導出來。S1代表最低尺寸區間的污染敏感度系數，通常為0～5 μm。

暴露在所有污染物分布下元件的流量退化量等于各個尺寸區間的污染物引起的流量退化量之和，其數學方程為:

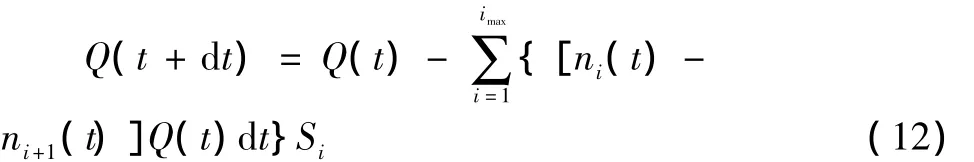
對更高尺寸區間:

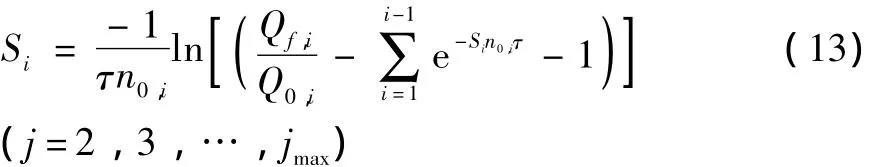
在現場工作條件下顆粒污染物不斷被磨滅，侵入的染物不斷代替由過濾器清除的污染顆粒使得系統保持在一個相對穩定的污染水平，因此油液污染濃度近似不變即:

式中:nf，i為在現場條件下的油液污染濃度，近似為定值。

將公式 (14)代入并積分，得到:

泵的流量從初始值降到最低允許值這段時間即泵的磨損壽命，根據公式 (15)可求得在現場實際條件下，泵的污染磨損壽命計算公式:

3 外嚙合齒輪泵污染磨損壽命分析

3.1 液壓泵污染敏感度試驗方法

通過上面的理論分析，得到外嚙合齒輪泵流量衰減的擬合公式、液壓泵污染敏感度數值與液壓泵污染壽命的計算公式，但是其中的加入污染顆粒前的流量Q0，i、加入污染顆粒后的流量 Qf，i等參數需要進行實際試驗測定。

液壓泵污染敏感度試驗方法是一種在試驗條件下評定液壓泵對污染物敏感程度的強化模擬方法，這種方法最初由美國俄克拉荷馬州立大學流體動力研究中心提出，已被接受為國際標準試驗方法［6］。

改進后的液壓泵污染敏感度試驗系統如圖2所示。

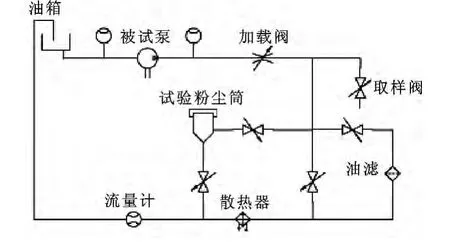
圖2 液壓泵污染敏感度試驗系統

試驗采用標準的ACFTD粉塵或者MTD試驗粉塵。為了縮短試驗時間，污染顆粒濃度應比較高，常用污染顆粒濃度為300 mg/L。試驗以尺寸最小的顆粒等級0～5 μm開始，分別加入油液污染濃度為300 mg/L的0～5 μm的試驗粉塵，使泵在額定工況下運轉，直到流量保持不變并穩定10 min，或運轉時間達到30 min。記錄泵在加入污染顆粒前的初始流量值及運轉一定時間后的流量值，之后將系統的污染顆粒過濾干凈，再分依次注入300 mg/L的0～10 μm，0～20 μm，0 ～ 30 μm，0 ～ 40 μm，0 ～ 50 μm，0 ～ 60 μm，0～70 μm，0～80 μm 的試驗粉塵，重復試驗，記錄流量數據。

3.2 外嚙合齒輪泵的污染敏感度

參考以E.C.Ftich教授為首的流體動力研究中心所得到的一組外嚙合齒輪泵污染敏感度試驗的數據如表1所示。

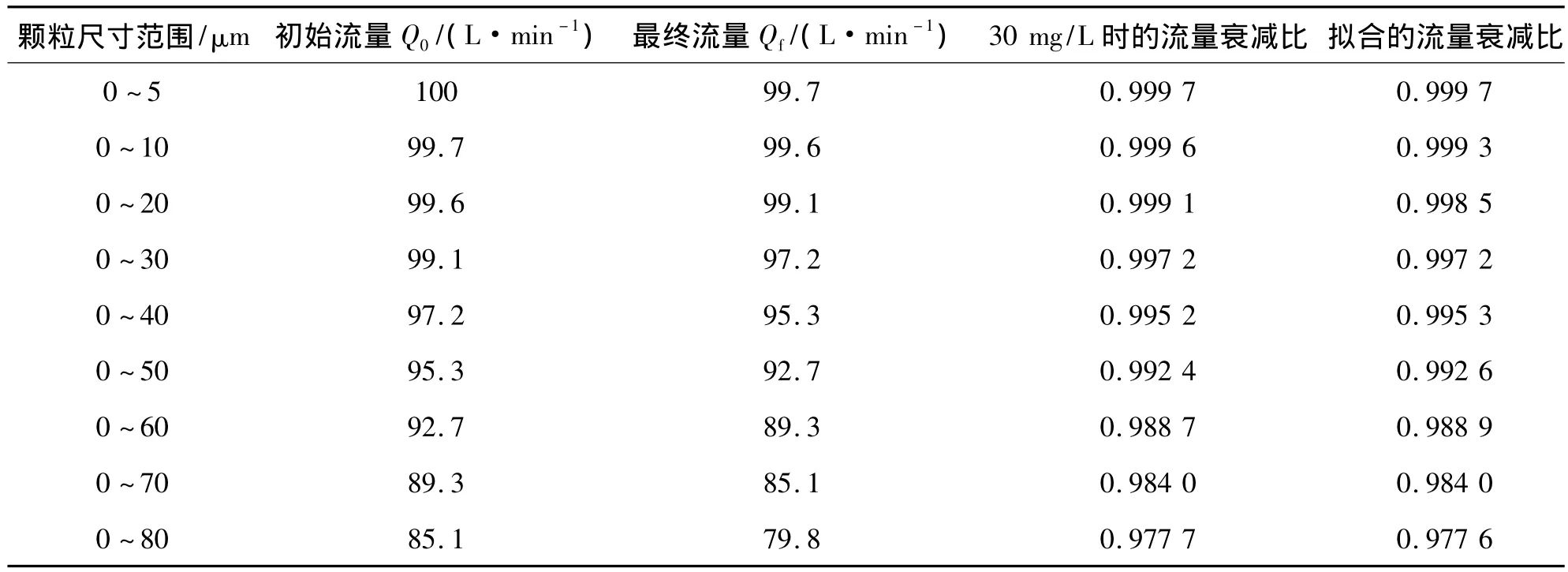
表1 外嚙合齒輪泵污染敏感度試驗數據

為了縮短試驗時間，液壓泵的污染敏感度試驗是在300 mg/L的高污染濃度下進行的，而Omega理論是在應用在污染濃度為30 mg/L的條件下，因此首先需要進行數據的標準化，利用線性模型將300 mg/L條件下的試驗數據變換到30 mg/L條件下:

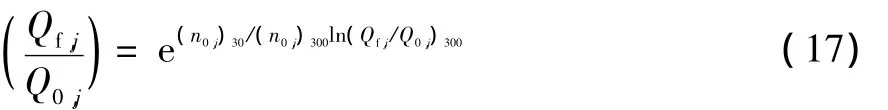
對污染敏感度試驗來說，Q0是每次加入污染顆粒前的流量，Qa為每次加入污染顆粒后的流量。根據外嚙合齒輪泵的磨損泄漏模型，將間隙h替換為侵入微粒的直徑D，可得到:

運用最小二乘法得到如下的方程，經試驗證明，根據這個方法所得出的曲線與實際試驗數據非常接近。

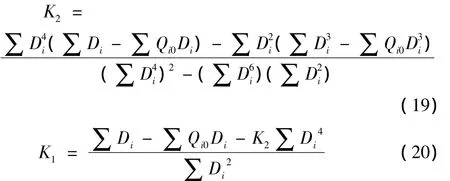
式中:Di為i尺寸范圍內的最大直徑;

Qi0為對系統注入i尺寸范圍污染物后的流量與初始流量之比。

得到這個流量退化擬合曲線之后，運用擬合所得到的 (Qf/Q0)fit數據和標準粉末油液的微粒分布數據代入公式 (11)和公式 (13)來計算泵的磨損污染敏感度系數。

由這組數據得到 K1=6.240 6×10－5;K2=3.401 9×10－8。擬合得到的流量衰減比如表1所示。

得到的齒輪泵的污染敏感度系數如表2所示。

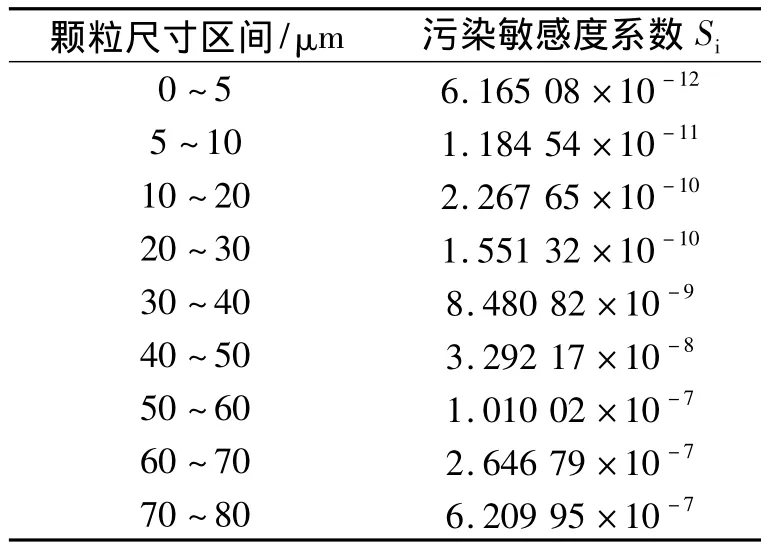
表2 外嚙合齒輪泵的污染敏感度系數

3.3 外嚙合齒輪泵的污染磨損壽命

取流量退化為額定流量的80%時視為泵失效。當油液等級為SAE5、SAE7、SAE9、SAE12時，每毫升油液中各個尺寸區間的顆粒數目如表3所示。

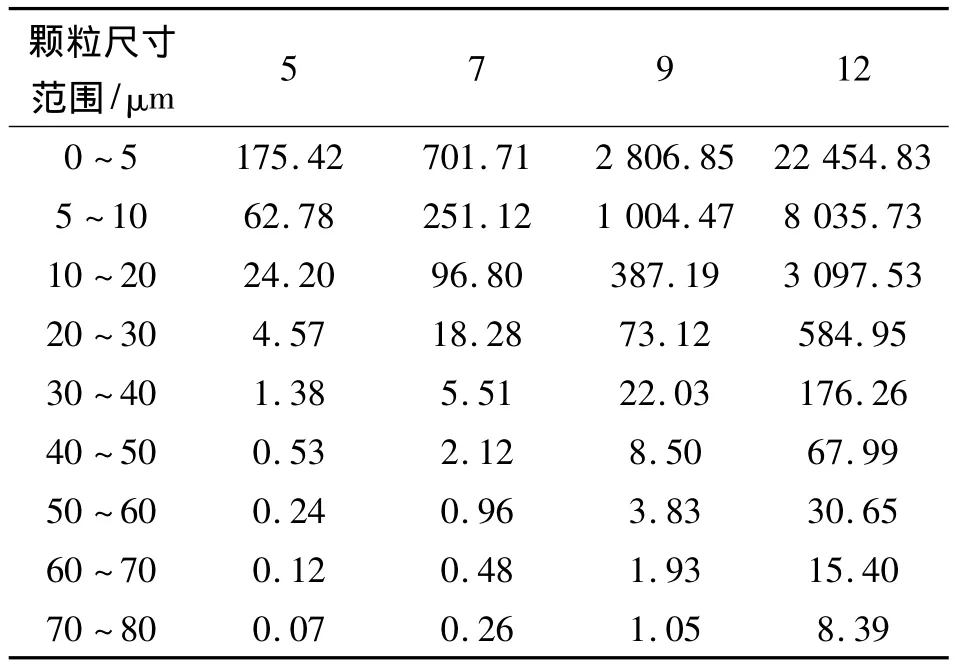
表3 每毫升油液中的顆粒分布

將上一步所求得的泵磨損敏感度數據和油液顆粒數據代入液壓泵的污染磨損壽命計算公式 (16)，可得到泵在SAE5、SAE7、SAE9、SAE12級油液下的污染磨損壽命分別為:SAE5級污染壽命為2 501.27 h;SAE7級污染壽命為625.32 h;SAE9級污染壽命為156.33 h;SAE12級污染壽命為19.54 h。

設置泵在SAE7級油液條件下，分別繪制出液壓泵工作壽命為1 000 h、2 000 h、3 000 h的污染耐受曲線，如圖3—5所示。

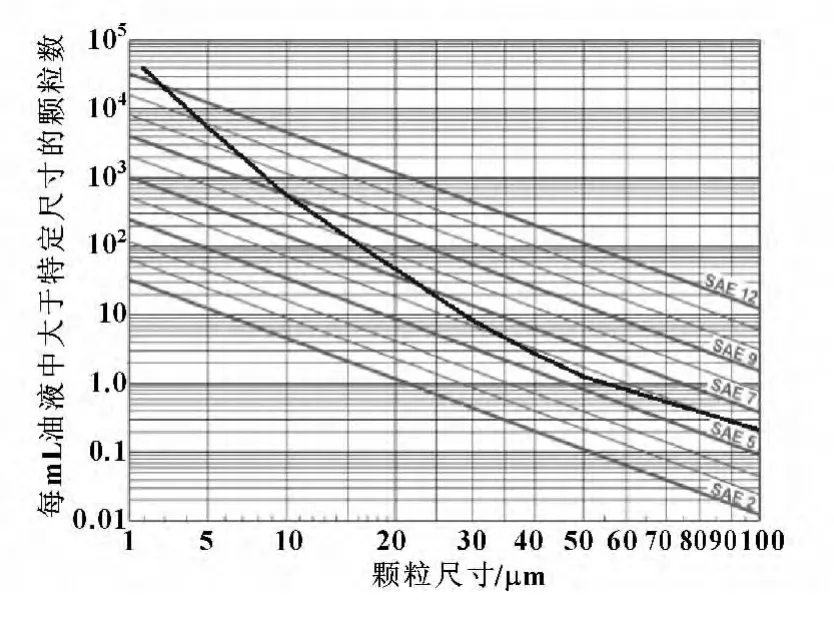
圖3 液壓泵工作壽命為1 000 h的污染耐受曲線

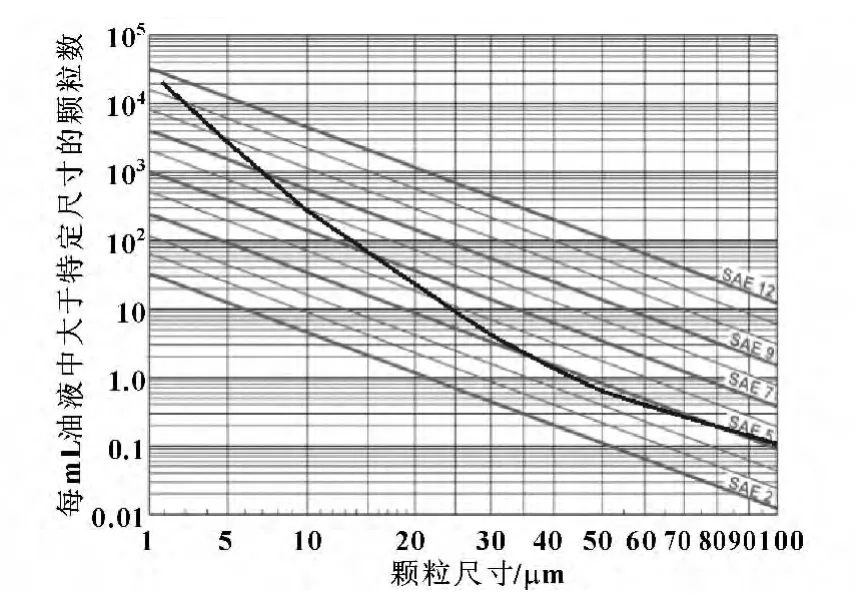
圖4 液壓泵工作壽命為2 000 h的污染耐受曲線

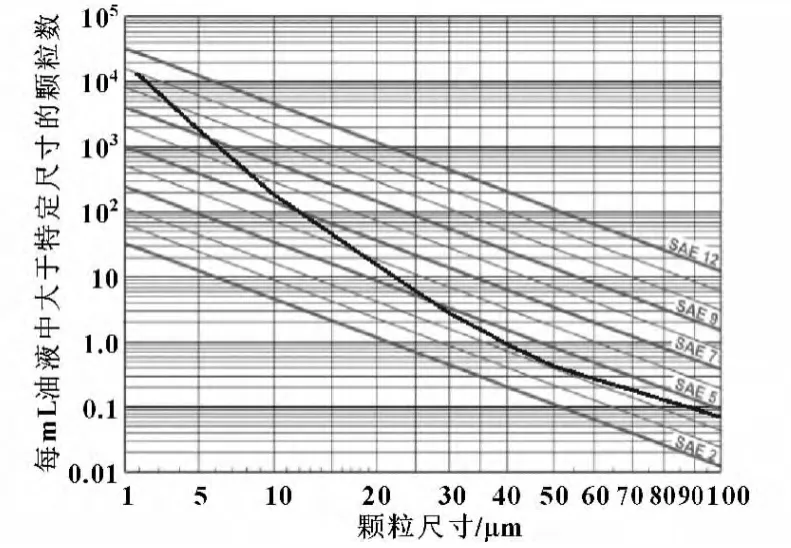
圖5 液壓泵工作壽命為3 000 h的污染耐受曲線

4 結論

在液壓元件污染敏感度試驗的基礎上做出改進并進行延伸，運用Omega理論，利用外嚙合齒輪泵的污染敏感度試驗數據計算獲得其污染敏感度系數和污染磨損壽命，克服了液壓元件污染敏感度理論缺乏對工程實際指導作用的缺點，通過這種方法能夠定量分析和比較各類泵的污染耐受性、預測受試泵在不同顆粒污染等級下的性能變化規律和污染磨損壽命。

【1】王強，涂群章，程建輝，等．液壓系統污染控制［M］．北京:國防工業出版社，2010．

【2】賈瑞清，夏志新．液壓元件污染磨損壽命的實驗室模擬研究［J］．液壓與氣動，1994(3):4－7．

【3】許賢良，趙連春，王傳禮．復合齒輪泵［M］．北京:機械工業出版社，2007．

【4】FITCH E C，HONG I T．Hydraulic System Design for Service Assurance［M］．Okal homa:BYDyne，Inc．，1999．

【5】FITCH E C，HONG I T．Hydraulic System Modeling and Simulation［M］．Okal homa:BarDyne，Inc．，2008．

【6】International Organisation for Standardisation．ISO/DIS9632．Hydraulicfluid Power-Fixed Displacement Pumps-Flow Degradation Due to Classified A．C．Fine Test Dust Contaminant-Test Method［S］．1991．

【7】Society of Automotive Engineers．SAE AS 4059E:2005．Aerospace Fluid Power-Cleanliness Classification for Hydraulic Fluids［S］．2005．

【8】李昆，高亞奎，劉紅．液壓泵污染壽命預測技術研究［J］．航空科學技術，2011(1):49 －52．