基于因子圖的分布式變分稀疏貝葉斯壓縮感知

朱翠濤，楊凡，汪漢新，李中捷

(中南民族大學 智能無線通信湖北省重點實驗室，湖北 武漢 430073)

1 引言

在認知無線電網絡中，動態頻譜共享機制分為覆蓋式（overlay）、共存式（underlay）和混合方式[1]。在這些共享機制中，除了對授權頻譜的使用情況進行檢測外，有關授權用戶的其他信息，如發送功率、位置、個數等也應及時、準確感知，才能避免對授權用戶造成干擾，實現頻譜安全共享。然而，在感知過程中，認知用戶接收的信號可能經歷了深衰落、陰影效應、噪聲等影響，使得單個認知用戶無法準確地對相關信息進行感知。于是，協同感知引起學者們的關注。文獻[2]在平均一致框架下，以相鄰節點的觀測作為約束通優化算法實現協同頻譜感知，利用約束條件迫使網絡中各認知用戶的頻譜感知結果達到全局最優。這種方法在協同用戶數目較多時會造成較大的網絡計算和通信開銷。為了克服此問題，文獻[3]在壓縮采樣的框架下，提出了一種基于一致優化的分布式寬帶頻譜壓縮感知算法，并引入加權的一致平均約束減少約束的數量，由此降低計算開銷及提高算法的收斂速度。為了改善協同頻譜檢測性能，文獻[4]結合一階馬爾可夫過程，通過貝葉斯推理及利用因子圖中的消息傳遞實現協同檢測任務。這些研究工作從不同角度對授權頻譜感知方法進行了深入探索。而在未來的認知無線電網絡中，多種頻譜共享機制會同時存在，為了避免相互干擾，授權用戶的其他信息也應及時感知。為此，文獻[5]提出了基于稀疏貝葉斯壓縮感知的聯合頻譜感知與定位算法，融合中心利用各認知用戶的壓縮測量值直接對授權用戶的信息進行估計。但是，基于相關向量機的稀疏貝葉斯壓縮感知算法復雜度較高，收斂速度慢。針對此問題，筆者在前期工作中[6]，提出了一種變分稀疏貝葉斯壓縮感知方法，改善協同感知性能。由于該工作是基于集中式協同感知，通信負載比較大，且頑健性較差。

基于此，本文在前期工作的基礎上，提出了一種基于因子圖[7]的分布式變分稀疏貝葉斯頻譜感知算法。該方法將聯合頻譜感知問題映射為因子圖模型，通過認知用戶鄰居間的置信傳播實現“軟融合”，且傳遞的信息非壓縮觀測值或本地決策值，而是前一次迭代過程中的融合信息。鄰居間傳遞的信息具有時間和空間相關性，充分利用這種二維相關性，提高認知用戶在低信噪比下的檢測性能。并將變分方法[8]用于稀疏貝葉斯框架中，簡化推理過程。同時，為了降低通信負載，算法在迭代過程中自適應地刪除不收斂的超參數及對應的基函數，從而減少分布式迭代過程中的通信量。

2 信號模型及問題提出

在認知無線網絡中，假定某檢測區域內有 Nch個授權信道，有 Np個處于活動狀態的授權用戶（簡稱PU），且 Np＜＜Nch。PU隨機分布在一定的區域里，其位置坐標表示為分別是橫坐標和縱坐標上的位置分辨率，表示位置識別精度。同時，檢測區域中存在 Nc個認知用戶（簡稱CR），其位置坐標分別表示為。任意CR通過無線信道接收任意授權用戶發射的信號，信號經過無線信道的路徑損耗為[9]

其中， Pt為發射功率， Pr為接收功率。路徑損耗與頻率、距離間的關系為[9]

其中， P0為一常量， n0為路徑損耗指數，由式（1）和式（2）可得接收功率與發射功率、距離及頻率之間的關系為

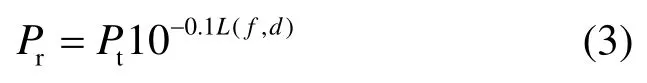
依據式（3），第k個認知用戶通過第i個信道接收在位置(xm, yn)的授權用戶發射的信號功率為

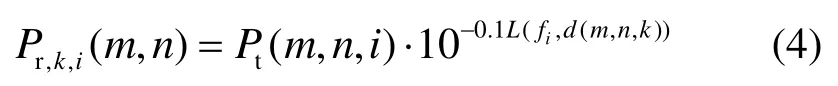
其中， Pt(m,n,i)表示在位置(xm, yn)處的授權用戶經過信道i發射信號的功率， fi表示第i個信道所對應的頻率，d(m,n,k)表示授權用戶與認知用戶k之間的距離，由式得到。那么，第k個認知用戶通過第i個信道接收可能來自各授權用戶的總信號功率為

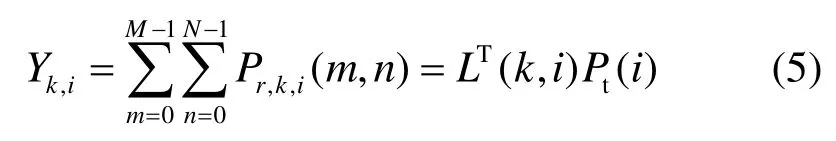
其中， P(i)表示經第i個信道接收可能來自各授權用戶發射信號功率組成的列向量， LT(k,i)表示各授權用戶發射信號的功率經信道i到達第k個認知用戶的路徑損耗組成的行向量。第k個認知用戶可能通過各信道接收的信號功率表示為由式（5）可得認知用戶對授權用戶進行感知的問題模型，用矩陣表示為

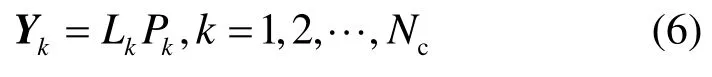
其中，矩陣 Lk中的第 i行表示為0表示1×MN的0向量。

3 壓縮感知模型

式（6）中包含了授權用戶的相關信息，本文采用全分布式的協同感知方法對授權用戶的相關信息進行感知。由于授權頻段的利用率低，認知用戶所接收的信號在頻域具有稀疏性。因此，利用壓縮感知理論，降低對寬帶信號采樣壓力。設第k個認知用戶在時域內檢測到的信號為 rk，根據傅立葉變換理論，可得

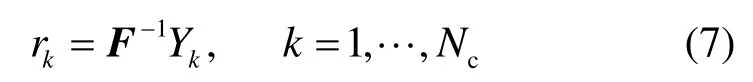
其中， F-1為離散傅立葉逆變換矩陣。由式（6）、式（7）可得

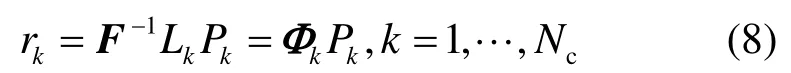
其中，kΦ為測量矩陣，它確定kr與kP之間關系。由于kL表示無線信道的路徑損耗，具有非常強的隨機性，kΦ滿足RIP[10]性質。在實際的傳播環境中存在噪聲干擾，式（8）變換為

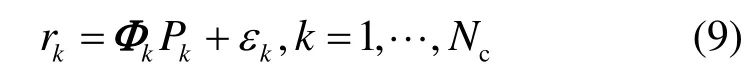
其中，kε表示均值為0，方差為2σ的高斯噪聲向量。針對問題（9），可以將其轉換為凸優化問題進行求解[11]，但是，算法的復雜度較高。本文充分利用貝葉斯推理的優勢，不需要恢復原始信號，直接依據觀測值kr及先驗信息進行相關參數的估計，并通過因子圖和變分方法將全局問題轉換為分布式的局部問題進行簡化求解。

4 變分稀疏貝葉斯推理

4.1 本地稀疏貝葉斯模型

稀疏貝葉斯壓縮感知過程實質上是基于概率圖模型的統計推理過程[12]。因此，可構造一個貝葉斯網絡模型描述線性回歸問題（9）的推理過程，如圖1所示。

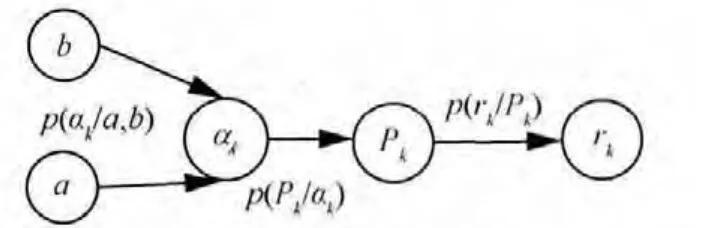
圖1 貝葉斯網絡模型

式（9）中，變量kε服從高斯分布，可推導出未知參量kP的似然函數服從均值為kkPΦ，方差為2σ的高斯分布，即

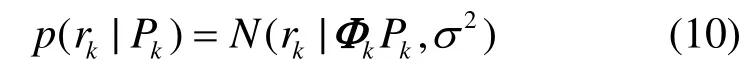
由于授權用戶隨機選擇一個信道進行數據發送，且大部分授權信道是空閑的，所以 Pk具有稀疏性。依據稀疏貝葉斯模型[12]，向量 Pk中的任意元素Pj服從均值為0，方差為αj的高斯分布，即

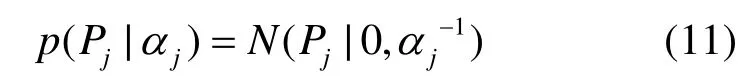
其中，jα為超參數，其物理意義是表示本地子信道的占用情況。當jα的數值變得很大時，根據高斯分布曲線特性，jα對應的jP會迅速衰減為0。又由于關于jα后驗分布大數據出現的概率非常大，這就決定了kP中大部分元素為0，即jα決定jP的稀疏性。由于超參數是變量，而且高斯分布方差的倒數的共軛概率分布為Gamma分布，因此，為超參數jα引入一個Gamma分布，即

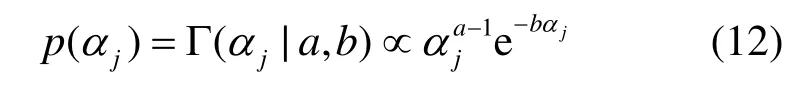
4.2 變分逼近

便于問題分析，在稀疏貝葉斯架構下，先形成協同頻譜感知的全局問題，然后逐步推導出分布式變分稀疏貝葉斯模型。為此，定義全局未知變量的集合為，觀測值集合，由式（9）可以得全局觀測值為

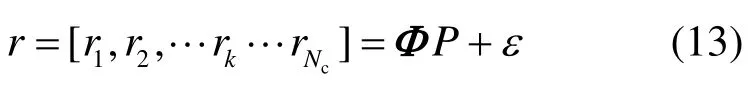
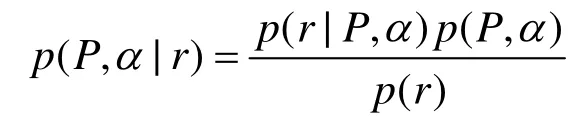
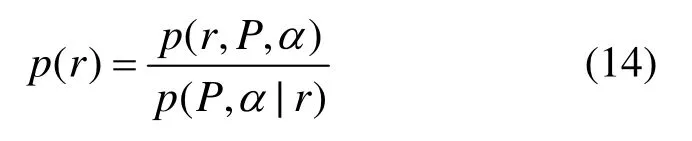
依據變分理論[8]，在式（14）中引入了一個關于變量P、α的q分布，其表達式為

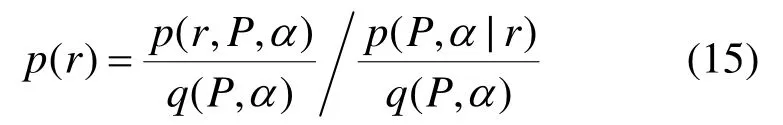
然后對式（15）兩邊取對數，又由于(,)qPα∫dd 1Pα= ，所以，式（15）可以轉換為

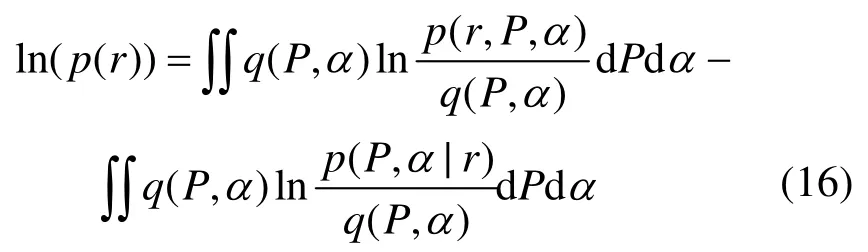
將式（16）簡記為

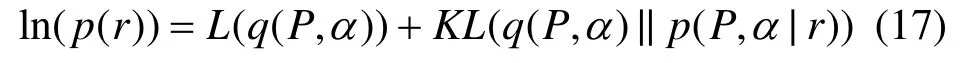
變分貝葉斯方法是通過最小化 KL散度尋找關于變量 P ,α的q分布，而KL散度依賴于難以求解的后驗分布。根據KL散度的特性可知，由式（17）可以推導出

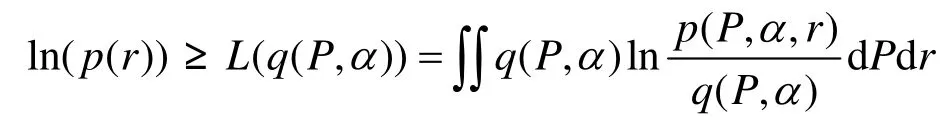
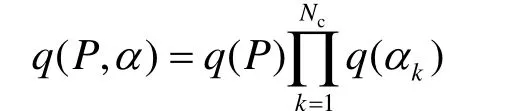
依據文獻[13]可以求得關于變量 P ,α的q分布的迭代優化更新表達式為

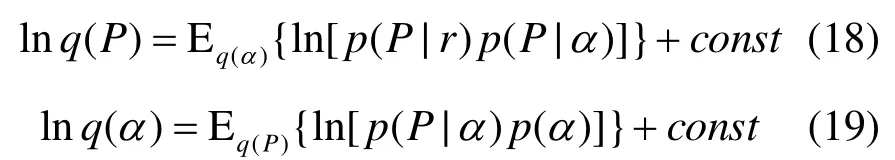
式（18）和式（19）中的 const表示與 P ,α獨立的部分。求解式（18）和式（19），可以得到關于變量 P ,α的q分布為

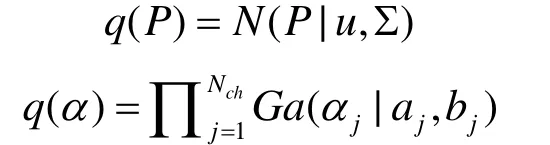
其中，

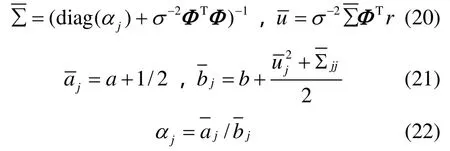
5 因子圖及置信傳播

5.1 因子圖表示

分布式的首要任務是將全局問題下的式（18）和式（19）轉換為分布式形式。如果已知認知網絡中的全局 q(P)分布，即參數u,∑為已知，那么可以根據式（21）在本地計算 q(α)中的參數，根據可以計算超參數α。這就意味著，只要每個認知用戶獲得了 q(P)，就可在本地更新計算q(α)。因此，只需將式（18）分解為分布式形式即可。為此，本文引入因子圖模型，通過和積算法實現鄰居間消息傳遞。引入 Nc個超參數向量分別與認知節點相對應，通過消息傳播使，即獲得 q(P)。

因子圖是一種用來描述如何將多變量的全局函數分解成多個局部函數乘積形式的雙向圖。利用因子圖模型刻畫式（18）的分布式形式，通過在相應的因子圖上分布地進行消息傳遞，實現q(Pk) = q (P)。相應的因子圖模型，如圖2所示。

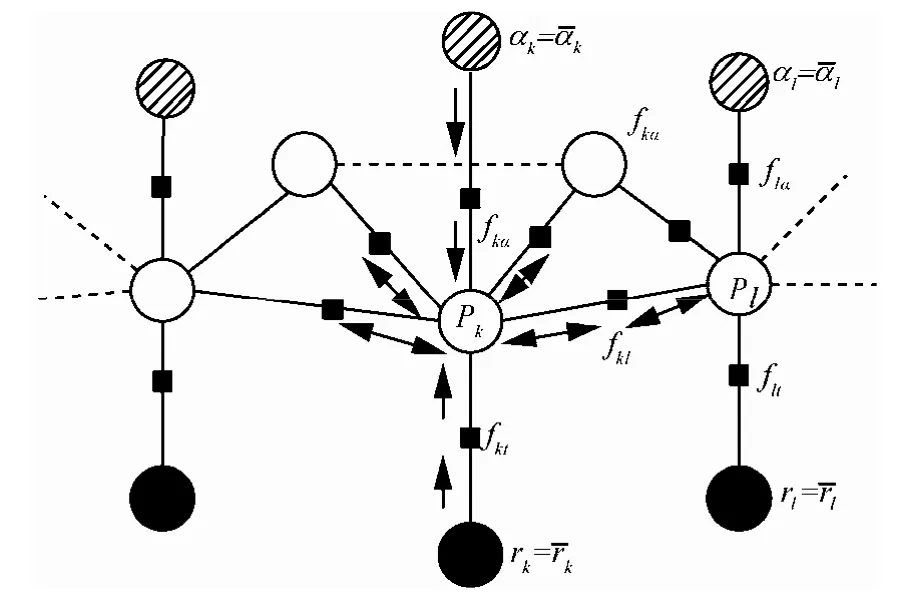
圖2 分布式稀疏貝葉斯因子

圖2 由節點（用圓表示）和因子（用黑方塊表示）組成，節點表示變量，因子表示節點之間的概率約束關系。其中，節點分為3個層次，最頂層是包含了所有認知用戶中的超參數集合，中間層是由未知參量集合組成，最下層由觀測向量的集合組成。其中，認知用戶間通過耦合因子 fkl進行信息交互。在因子圖中，對于任意認知用戶k，節點αk與節點Pk間的因子定義為[14]

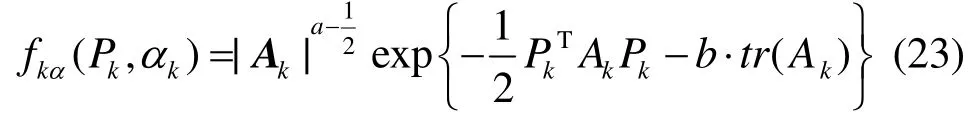
其中， Ak是由超參數組成的對角矩陣。節點 Pk與節點 rk間的因子定義為

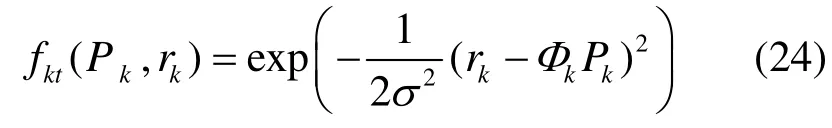
為了實現相鄰認知用戶間進行信息交互，在相鄰認知用戶間定義耦合因子為

其中，β為耦合參數，β值越大，相鄰節點間的耦合性越強。

5.2 置信傳播及q(Pk)分布式求解

依據圖2消息傳播過程為：首先，從節點αk到因子發送消息δ(αk-αk)為二元指示函數，即

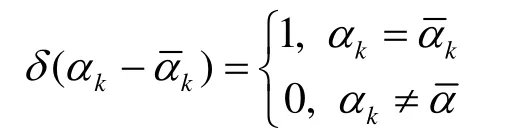
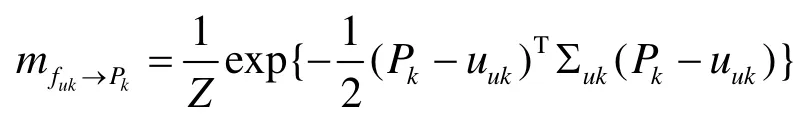
根據和積算法，關于 Pk的邊緣分布可以表示為接收到所有消息的乘積并歸一化，即

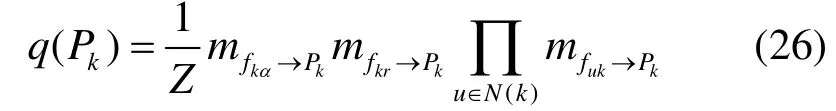
依據式（26）可推出 q(Pk) 的分布為高斯分布，即

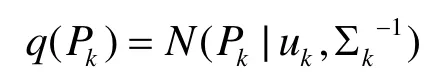
從節點 Pk到其他鄰節點 Pl發送的消息定義為

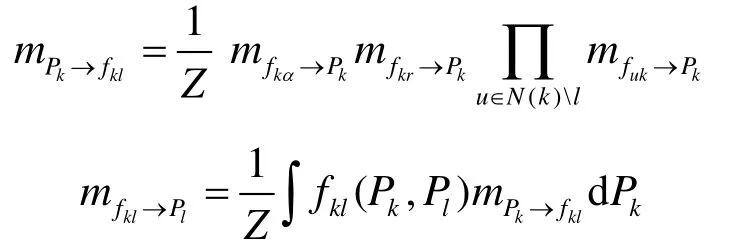
由此可以推導出相鄰節點間傳遞消息的均值和方差為

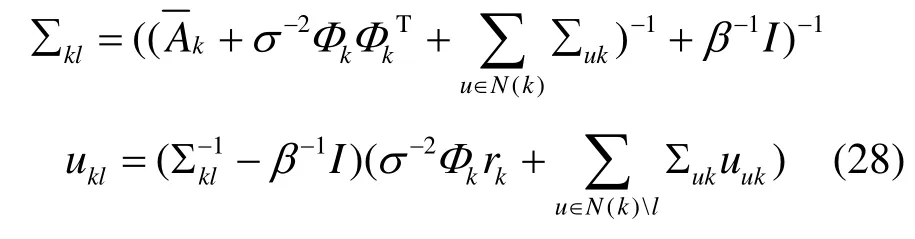
5.3 算法總結

各認知用戶在計算邊緣分布 q (Pk) 時，消息在鄰居之間相互傳播會形成環，為了使算法能夠收斂，本文采取的主要措施為：1）各節點同步更新消息；2）尋找合適的收斂條件。依據式（27），第k個認知用戶所對應的邊緣參數在第I次迭代中的表達式為

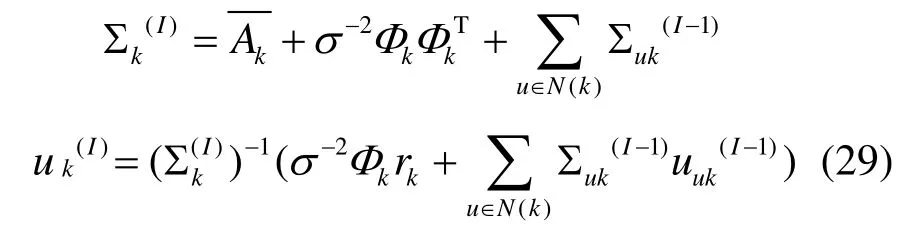
同樣，根據式（28）定義在第I次迭代中相鄰2個節點k、l間傳遞消息的均值與方差為

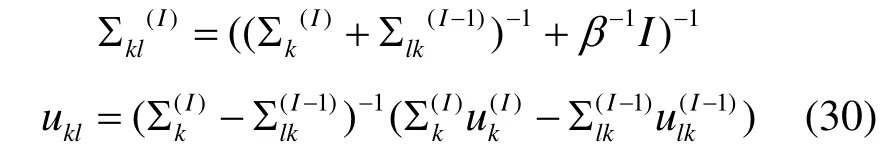
算法的具體步驟如下。

4) 計算邊緣參數∑k、uk，更新超參數αk,j。如果超參數大于門限值thθ時，刪除此超參數及相應的基函數。根據變分稀疏貝葉斯收斂條件判斷變分貝葉斯學習算法是否收斂，若不收斂跳轉到步驟2）。

5) 用循環可信度傳播算法計算最后的邊緣參數，結束算法。

6 算法性能分析

6.1 收斂性

根據式（20）和式（22）迭代尋找變量P的q分布時，會導致不相關的超參數α不收斂。為了簡化計算以及算法快速收斂，本文對超參數α設置門限值，算法在迭代過程中刪除不收斂的超參數以及相應的基函數。在分布式變分稀疏貝葉算法中引入了循環可信度傳播，為了確保算法的收斂性，本文采取同步工作機制，各CR同步更新消息。同時，通過大量實驗，尋找最佳的收斂條件，具體為：第I次迭代計算的邊緣參數 uk(I)和 ∑k(I)與前一次計算結果的絕對值差小于 1 0-3作為算法收斂的收斂條件。

6.2 算法復雜度

算法復雜度與迭代次數、相鄰節點個數及消息大小有關。假定認知用戶k的相鄰用戶有N(k)個，傳播消息大小為H，那么節點k接收的總消息大小為 H N(k)。節點k加上自身的檢測消息大小為假定迭代次數為I，則算法總的復雜度為

6.3 通信負載

相鄰節點間互相傳遞消息，實現消息共享。但是隨著消息傳播，網絡負載也會增加。本文在實現過程中，相鄰CR之間傳遞估計值，而不是原始的觀測數據。同時為了進一步降低網絡負載，本文在算法的迭代過程中自適應地逐步刪除不收斂的超參數以及基函數，減小相鄰用戶間的通信量，從而降低網絡負載。

7 實驗及分析

為了驗證算法的有效性，在MATLAB仿真平臺上進行了數字仿真實驗。在后繼的所有仿真實驗中，設定認知網絡中待感知的頻率范圍為[0,…,800] MHz，分為 20個子信道。并假設存在8個授權用戶分布在10×10區域內，，每個授權用戶的發射功率定義在[10,30] mW區間內隨機取值。在此區域里分布了3個認知用戶，分別設置在(6.1, 8.2)，信噪比為-5 dB。耦合參數，門限值利用本文提出的分布式變分稀疏貝葉斯算法進行頻譜檢測，認知用戶CR1檢測的結果如圖3所示。其他認知用戶CR2和CR3也有類似的檢測結果。通過大量實驗，算法迭代次數平均為4次。

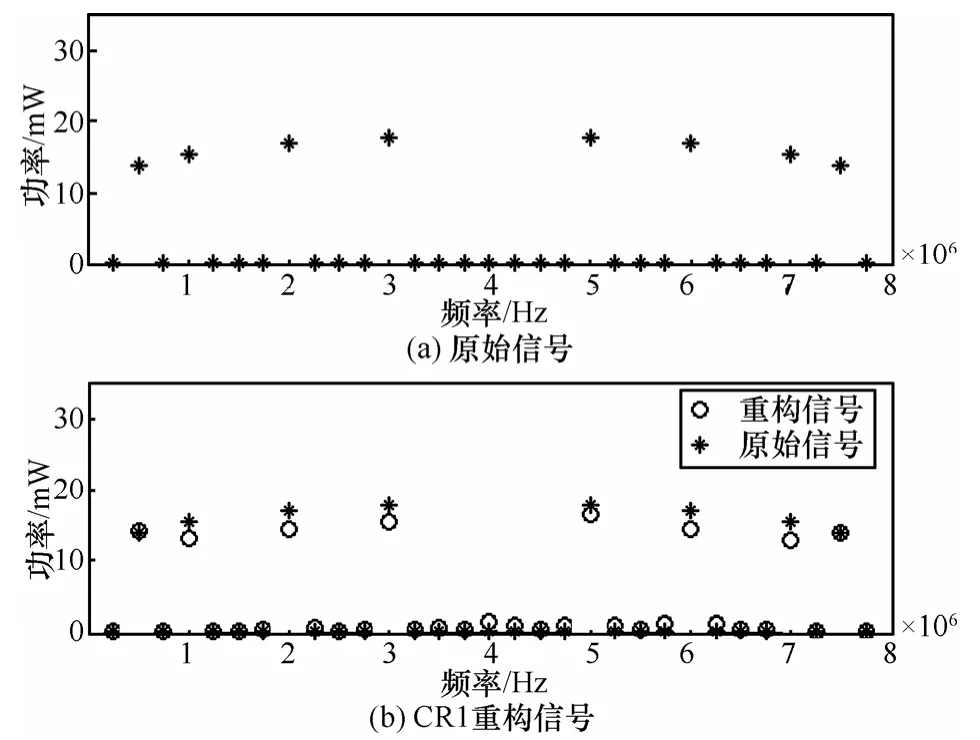
圖3 認知用戶CR1重構結果與原始信號比較

在相同的設置環境下，利用三維坐標對授權用戶的位置信息，以及相應信道的占用情況進行了檢測。圖4為CR1檢測到的有關授權用戶信息，圖中星號代表授權用戶在地理坐標上實際的信道使用情況，圓圈代表CR用戶能夠檢測到的授權用戶在地理坐標上實際的信道使用情況。從實驗結果可以看到，CR1用戶能檢測出授權用戶的位置信息及占用的信道。同樣，其他CR用戶也有類似的檢測結果。

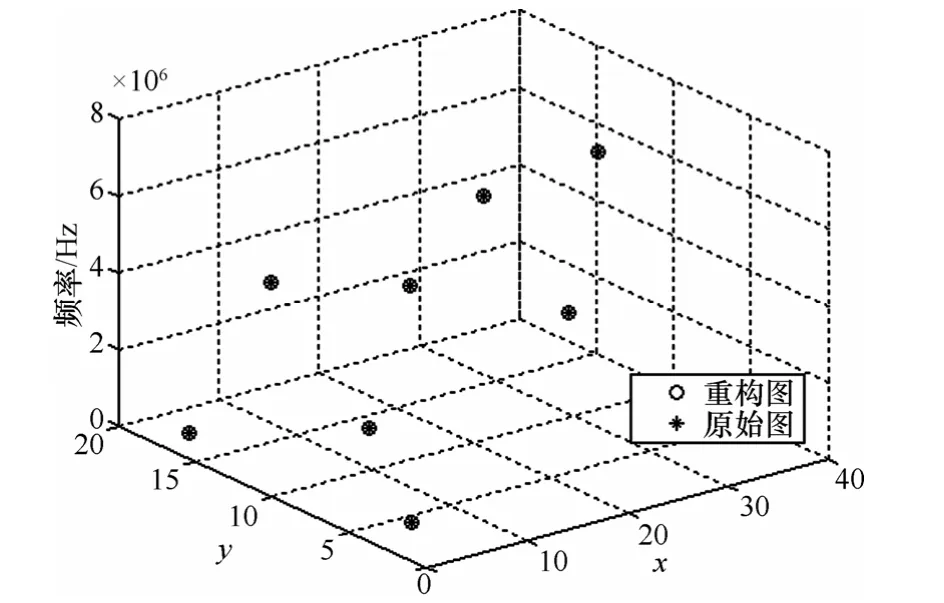
圖4 CR1用戶檢測的授權用戶信息

在此基礎上，又驗證了所提算法在不同采樣率，不同信噪比下的檢測性能。信噪比分別設為0 dB、5 dB、-5 dB下，采樣率分別為0.2、0.3、0.4、0.5、0.6、0.7、0.8。各認知用戶的檢測概率和誤檢測概率，其中，CR1檢測概率結果如圖5和圖6所示。

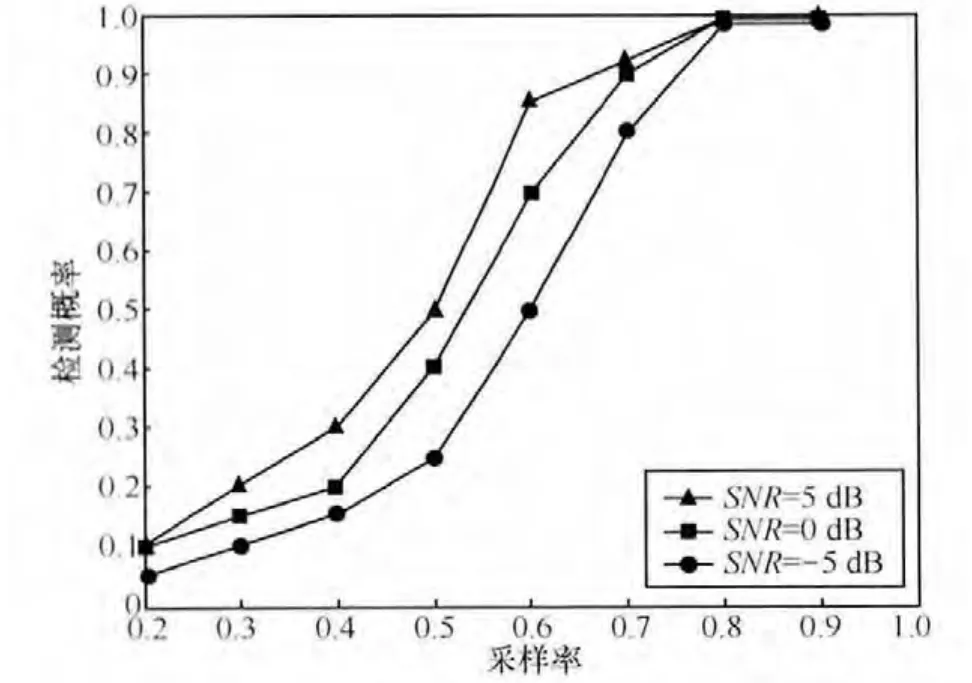
圖5 不同采樣率下的檢測概率

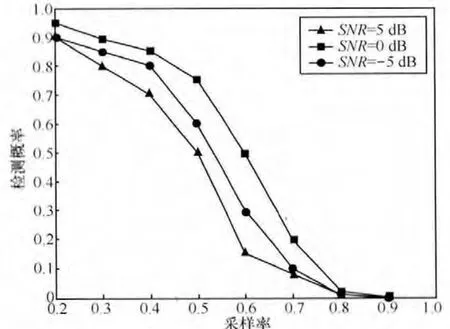
圖6 不同采樣率下的誤檢概率

從實驗結果可知，隨著采樣率增加，檢測概率隨著增加，誤檢測概率隨著降低。為了減輕對寬帶信號采樣壓力，本文在協同感知算法中引入了壓縮采樣，由此導致了感知算法性能的退化。

同時，在SNR=5 dB，壓縮比為50%，3個協同認知用戶，耦合參數β和門限值thθ取不同值情況下，從均方誤差 MSE和 ROC(receiver operating characteristic)2個方面，將本文提出的基于因子圖的分布式變分稀疏貝葉斯壓縮感知(DVSBL)算法與集中變分稀疏貝葉斯壓縮感知(CVSBL)算法[6]，以及基于相關向量機的集中式稀疏貝葉斯感知(CSBL)算法[5]進行了對比分析，如表1和圖7所示。

在基于因子圖的分布式變分稀疏貝葉斯算法中存在β和thθ2個參量，取值的大小會影響算法的感知精度，而在集中式算法中只存在參數thθ。當thθ相同，β取不同值時，CVSBL算法的MSE相同，DVSBL算法有所變化。當β和thθ增大時，DVSBL算法的性能趨于最優。表1中的數值為多次實驗結果的平均值。

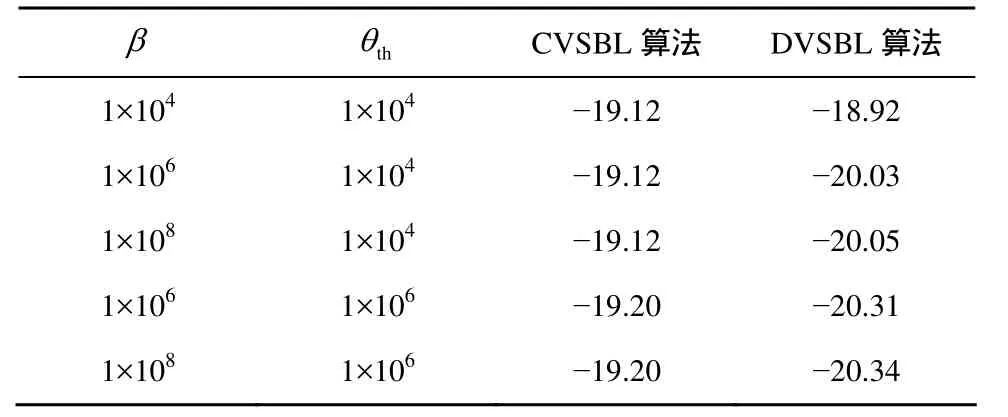
表1 不同β和thθ情況下2種算法的MSE比較/dB

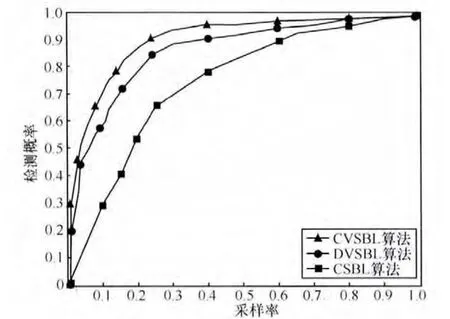
圖7 3種感知算法的ROC比較

從圖7實驗結果可以看出，CVSBL感知方法的效果最好，但由于所有認知節點要將本地的觀測值傳給融合中心，通信負載大，頑健性差。CSBL算法具有較高的計算復雜度，并擁有CVSBL算法的缺陷。本文提出的DVSBL方法，在沒有融合中心的前提下，它的ROC 性能近似最優，且算法復雜度和通信負載較低。

8 結束語

在未來的認知無線電網絡中，多種共享機制會并存。要實現安全的頻譜資源共享，必須對授權用戶及頻譜的占用情況及時、準確感知。但是，由于無線信道的復雜性和不確定性，使得相關信息的準確感知面臨許多困難。針對此問題，本文探索性地將因子圖引入到分布式頻譜感知模型中，并采用變分近似降低計算復雜度。同時算法在計算過程中，不需要稀疏參數間交叉調整，進一步提高計算速度。

[1] CHAKRAVARHY V, LI X, WU Z, et al. Novel overlay/underlay cognitive radio waveforms using sd-smse framework to enhance spectrum efficiency-partⅡ: analysis in fading channels[J]. IEEE Transactions on Communications, 2010, 58(6):1868-1876.

[2] ZHI T. Compressed wideband sensing in cooperative cognitive radio networks[A]. The IEEE Global Communications Conference [C]. New Orleans, LA, USA, 2008.

[3] 曾凡仔，劉潔，李仁發等. 基于一致優化的分布式寬帶合作頻譜感知算法[J]. 通信學報,2011,32(9):147-152.ZENG F Z, LIU J, LI R F, et al. Distributed cooperative spectrum sensing based on consensus optimization[J]. Journal on Communications, 2011,32(9):147-152.

[4] WANG Z X, YANG T. Markov compressive sensing in cognitive radio using factor graph[J]. Information and Electronic Engineering, 2012,10(4):396-400.

[5] XUE L, STEVEN H, ZHU H, et al. Bayesian compressed sensing based dynamic joint spectrum sensing and primary user localization for dynamic spectrum access[A]. The IEEE Global Communications Conference[C]. Houston, Texas, USA. 2011.

[6] 朱翠濤，楊凡. 基于變分稀疏貝葉斯學習的頻譜檢測方法[J]. 中南民族大學學報(自然科學版), 2013, 32(1):65-69.ZHU C T，YANG F. Spectrum detection based on variational sparse Bayesian learning[J]. Journal of South-Central University for Nationalities(Nat Sci Edition), 2013, 32(1):65-69.

[7] KSCHISCHANG F R, FREY B J. Factor graphs and the sum-product algorithm[J]. IEEE Transactions on Information Theory, 2001, 47(2):498-519.

[8] BISHOP C M, TIPPING M E. Variational relevance vector machines[A]. Proceedings of the 16th Conference on Uncertainty in Artificial Intelligence[C]. San Francisco, CA, USA, 2000. 46-53.

[9] RAPPPOT T S. Wireless Communications: Principles and Practice[M].Prentice Hall PTR, 2002.

[10] HONG S. Direct spectrum sensing form compressed measurements[A].The IEEE Conference for Military Communications[C]. California,USA, 2011. 1187-1192.

[11] BAZERQUE J A, GIANNAKIS G. B. Distributed spectrum sensing for cognitive radio networks by exploiting sparsity[J]. IEEE Transactions on Signal Process, 2010, 58(3):1847-1862.

[12] JI S, XUE Y, CARIN L. Bayesian compressive sensing[J]. IEEE Transactions on Signal Process, 2008, 56(6):2346-2356.

[13] BISHOP C M. Pattern Recognition and Machine Learning(Information Science and Statistics)[M]. Singapore: Springer,2006.

[14] BUCHGRABER T, SHUTIN D. Sparse Bayesian consensus based distributed field estimation[A]. The 5th International Conference on Signal Processing and Communication Systems[C]. Honolulu, USA, 2011.