基于判別性降維的字典學習在人臉識別的應用

李 行

(廣西教育學院數計系，廣西南寧 530023)

人臉圖像通常是高維度的，這會導致存儲空間大并且增加了計算量［1］，同時降低了人臉識別的判別性［2］。因此，學者們提出了許多降維(Dimensionality Reduction，DR)技術來降低人臉圖像的維度和加強判別特征，這些方法很容易使用，但是，用于解決表情和姿勢改變問題時并不是很高效，當訓練樣本不充足時，這些方法學習到的子空間將會有偏差［3］。

人臉識別(Face Recognition，FR)的子空間方法中，通常使用最近鄰(Nearest Neighbor，NN)分類器［3］和 SVM 進行分類［4］。最近提出了一種新的人臉分類方案，基于分類的稀疏表示(Sparse Representation Coding，SRC)［5］。SRC分類器顯示出非常有競爭性的性能，但是當每類的訓練樣本不充足時，它的性能會下降。前人已經開展了許多工作來調查SRC中的降維問題，例如文獻［6］為SRC中的降維問題提出了一種無監督的學習方法，相對于PCA和隨機投影實現了更高的識別率，也因此驗證了一個設計良好的降維方法可能有益于稀疏分類方案。文獻［7］中提出了一種元臉學習(MFL)算法來表示訓練樣本，它通過學習每個類獲得一系列“元臉”。基于經典KSVD算法［8］，文獻［9］介紹了一種DKSV算法對查詢圖像編碼，它利用編碼系數進行分類工作。文獻［10］提出了一種監督式算法對圖像分類任務來學習一個字典和一個分類器。文獻［11］提出了一種類獨立監督式同步正交匹配追捕方案，它解決了當類內維度增加時的字典學習問題。最近，文獻［12］提出了一種Fisher判別字典學習(Dictionary Learning，DL)算法來解決基于模式分類的稀疏表示，它相對于其他基于模式分類方案的字典學習顯示出了具有競爭力的性能。

上述文獻表明，聯合DR和DL過程可以實現更高效的識別。因此，本文提出了基于判別降維的字典學習(DDR－DL)方法來利用訓練樣本中高效、魯棒的判別信息，使來自不同類的人臉圖像的特征可以通過一個子空間中的字典高效地分開。實驗結果表明了所提算法的有效性及高效性。

1 算法設計

1.1 模型

為了更高效地利用訓練集A中的判別信息，本文提出了學習DR矩陣P和字典D，這樣可以實現一個更精確的分類。對于投影矩陣P，本文期望它可以保存A的能量同時使不同的類Ai在由P定義的子空間中可分割。為此，本文提出了一種正交投影矩陣，它可以同時最大化A的總散射和A的類間散射。對于字典D，期望它能夠如實地表示降維數據集PA，同時使來自相同類的樣本更靠近由跨越D空間中的其他樣本。基于以上考慮，本文提出了聯合判別式降維和字典學習(DDR－DL)模型來最優化P和D，即

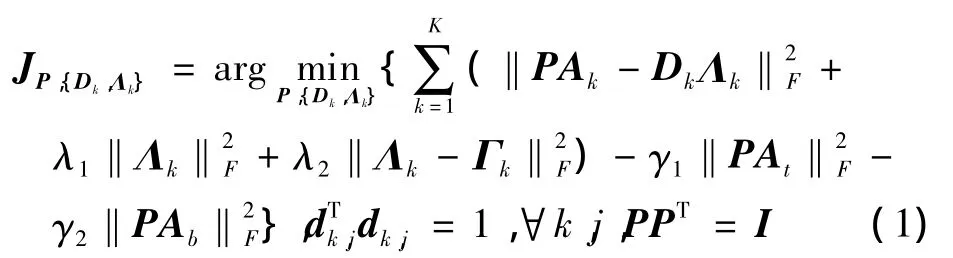
式中:Dk是類k的子字典，D=［D1，D2，…，DK］產生了全部字典;Λk表示Dk上PAk的編碼系數矩陣;At表示集中訓練集，如At=A－M，M的每一列表示A中所有樣本的平均向量m;Ab是A的特定類的集中數據集，如Ab=［M1－M，…，MK－M］，MK的每列是Ak中樣本的平均向量mk;Γk是一個矩陣，它的每列表示Λk中每列的平均值;λ1，λ2，γ1和 γ2是正標量。字典 Dk的每個原子dk，j要求有單位規范。

式(1)中的DDR－DL模型，目標投影P和字典D會使得訓練樣本大于類間的距離，小于類間的變化。理想地，如果P和D可以得到較好的優化，可以獲得查詢樣本y更準確的分類。接下來討論如何做到式(1)的最小化。

1.2 最優化

式(1)中的DDR－DL目標函數是非凸的。本文使用一個兩級選擇性方向方法來解決，將全部最優化分割為兩個子問題;固定投影矩陣P，解決字典D和系數Λ;固定D和Λ來更新P。選擇性和迭代地解決這兩個子問題，然后在一個較優點停止以得到P和D的局部最優方案。因為算法僅可以得到一個局部最優解，不同的P和D的初始化會導致不同的最終解。本文的算法使用PCA來初始化P，利用原始訓練集來初始化D。如果隨機地初始化D，可以實現相同的分類率，盡管已解決的D對于不同的初始化是不同的。后面將展示全局最優化算法。具體步驟為:

1)初始化P。利用PCA來初始化P，也就是說，初始P訓練數據A的PCA轉換矩陣。

2)固定P，解決D和Λ。這種情況下，式(1)中的目標函數變為

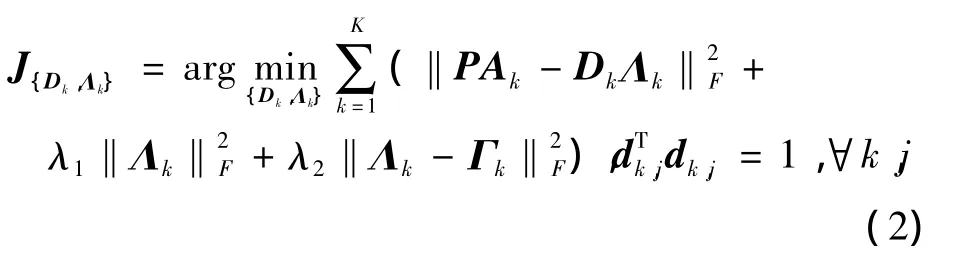
顯然，上面的目標函數可以分割為K個子問題，可以單獨最優化每組{Dk，Λk}為

Dk和Λk同樣是選擇性和迭代地得到解決。為了使最優化更簡單，本文初始化Dk為0，在接下來的迭代中Γk可以計算為更新系數矩陣Λk的列平均矩陣。因此，Γk可以看作是每次迭代中的一個最優化Dk和Λk的已知常數矩陣。

從Dk的一些初始化中(例如隨機初始化)可以計算編碼系數Λk。在每次迭代中，一旦給定Dk，便可容易地得到Λk的易于分析的解

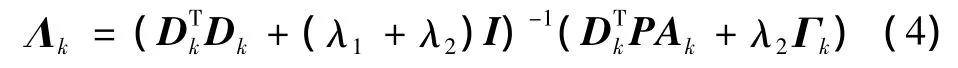
當獲得Λk時，字典Dk接著可以得到更新［6］。

經過若干次迭代后，可以獲得所有的Dk和Λk，因此可以獲得全部字典D和關聯系數矩陣Λ。

3)固定D和Λ，更新P。定義X=DΛ，式(1)中的目標函數可以表示為

上面的子目標函數JP是自身非凸的，它將有一個局部最小值，首先，因為PPT=I，將有

為了解決上面在目前迭代h的最小化問題，本文使用φ(P(h－1))接近式(7)中的φ(P)，其中P(h－1)是迭代h－1次獲得的投影矩陣。通過使用特征值分解(EVD)技術，得到

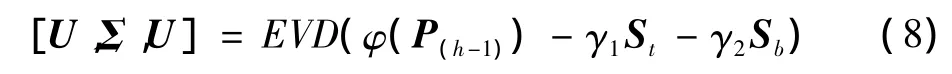
式中:Σ 是(φ(P(h－1))－γ1St－γ2Sb)的特征值形成的對角矩陣。然后可以將更新的P作為U中最重要的l個特征向量，例如，定義P(h)=U(1:l，:)。但是，這樣P的更新將會很大，使得式(1)中的整個系統的優化不穩定。因此，本文選擇在每次更新中逐步更新P，定義

式中:c是一個小的正數來控制迭代中P的變化。

4)停止迭代。如果到達最大迭代數，或者鄰近迭代目標函數JP，{Dk，Λk}之間的差別小于一個預設值ε，然后停止并輸出P和D。否則回到步驟2)。

1.3 DDR－DL模型的收斂

式(1)中提出的DDR－DL模型對于未知變量是聯合非凸的，因此1.2節中提出的最優化算法可以至多到達一個局部最小值。在步驟2)中，當另一個是固定時，子問題對于每個{Dk，Λk}是凸的，該算法將會使該問題產生一個局部最小值。但是，在步驟3)中，式(6)對于式(4)中的原始子問題是一個近似化描述，因此獲得的解僅是子問題中的局部最小值的一個近似。總之，本文算法的收斂不能得到保證，但是根據經驗可以得到一個穩定解。

使用AR數據庫和MPIE數據庫作為例子來說明DDR－DL的最優化過程。人臉圖像的維度降至300，在兩個數據庫中，目標函數JP，{Dk，Λk}對迭代次數的曲線分別在在圖1a和圖1b中描述，其中，參數值為λ1=λ2=0.005，γ1=10，γ2=1 。

圖1 DDR－DL算法在AR和MPIE數據庫中的收斂曲線

從圖1可以看出，經過若干次迭代(如6次迭代)，目標函數的值會變得穩定，它僅在小范圍內變動。通常，迭代會在15次之內停止。實驗結果同樣表明停止多或少的迭代的最小化，得到的投影P和字典D將會產生幾乎相同的FR率。這說明盡管提出的DDR－DL算法不能產生理想的收斂，它對迭代次數并不敏感，實驗設置最大迭代次數為15，表現效果良好。

1.4DDR－DL分類方案

得到投影矩陣P后，查詢樣本y可以通過Py投影到一個更低維度空間中，然后更低維度特征Py可以在字典D上編碼。這里采用帶有編碼用的l2—基準規則化的聯合表示模型

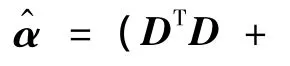
當計算得到編碼向量，可以基于每類的重構剩余來實施分類，像 SRC［6］或 CRC［10］中那樣。但是，在提出的DDR－DL算法中，每個類的編碼向量Λk的平均值同樣可以通過學習得到，可以表示為uk，和uk之間的距離對于分類同樣有幫助，因此，本文采用文獻［3］中的分類器來進行最后的分類工作

式中:ω是平衡2個項的常數。最終的分類是利用identity(y)=arg mink{ek}實施的。

2 實驗分析

所有的實驗均在4 Gbyte內存Intel(R)Core(TM)2.93 GHz Windows XP機器上完成，編程環境為MATLAB 7.0。

實驗利用AR和MPIE兩大通用人臉識別數據庫來驗證提出的DDR－DL算法的性能，并與SRC框架下的字典學習和/或降維方法的表示算法進行比較，包括DRSRC［6］，MFL － SRC［6］，PCA+SRC［7］，PCA+CRC［8］，FDDL［9］，LDA+SRC［10］，LDA+CRC［11］方法，每個數據庫中，首先測試這些比較方法對于訓練樣本數量的魯棒性，然后顯示特征取不同維度時的結果。

2.1 參數選擇

式(1)中的 DDR －DL 模型中有 4 個參數 λ1，λ2，γ1，γ2。這4個參數都有非常清楚的物理含義，它們可以只帶這些參數的設置。(λ1，λ2)是用來更新投影矩陣P和編碼系數Λk，(γ1，γ2)是用來更新降維中的投影矩陣。因此在參數選擇中，可以決定 (λ1，λ2)，然后確定 (γ1，γ2)。從式(3)可以看出λ1和λ2的設置可以同時規則化編碼系數Λk并通過最小化Λk的類間散射介紹判別性。因為Dk的每個原子(如列向量)有一個單元l2—基準，可以基于實驗經驗設置λ1=λ2=0.005。

參數γ1，γ2的設置和降維投影矩陣P的學習有關。它們相對于λ1，λ2應該設置得更大一些，因為如果僅有式(1)中的3項工作時會得到不重要的解(如P≈Null(A)，也就是PA≈0)，設置γ1=10，γ2=1 ，主要用來最大化訓練樣本的總散射，同時介紹一些類間的判別。在測試階段，通過經驗設置所有實驗中的標量λ(參考式(10))為0.001 和 ω (參照式(11))為0.01。

2.2 AR人臉數據庫

AR數據庫由來自126人的超過4 000張正面圖像，對于每個人，提取26張來自2個單獨部分的圖像，圖2所示為AR人臉庫的樣本示例。

圖2 AR數據庫的樣本示例

實驗使用包含50位男性和50位女性的6種光照和8種表情變化的數據集，從每個對象中隨機選取2～7個樣本進行訓練，其他樣本用來作為查詢樣本，將所有的樣本投影到一個550維子空間中(將LDA+SRC和LDA+CRC方案中的樣本投影到一個99維子空間中)。重復實驗50次來計算平均識別率和相應的標準偏差。對比方法的FR率在表1中顯示。

表1 在AR數據庫上不同數量訓練樣本的識別率

從表1可以看出，當每類的訓練樣本不是很小時，如每個類7個樣本，所有方法的識別率下降，特別是LDA+SRC和LDA+CRC。這主要是由于LDA對訓練樣本數敏感。提出的DDR－DL在所有方法中實現了最高的FR率。特別地，它對于小的樣本問題不敏感。當每類的訓練樣本數相對較高例如每類6或7個樣本，DDR－DL的識別率和FDDL十分相近，但是，當訓練樣本數相對較低時例如每類2～5個樣本，DDR－DL和其他方法的差距將會變大。總之，DDR－DL的性能是很穩定的。

接著評估不同維度下的DDR－DL的性能。從每個對象中隨機選擇4個樣本進行訓練，所有剩下的圖像作為查詢圖像，各種方法的不同特征維度的識別率如表2所示。

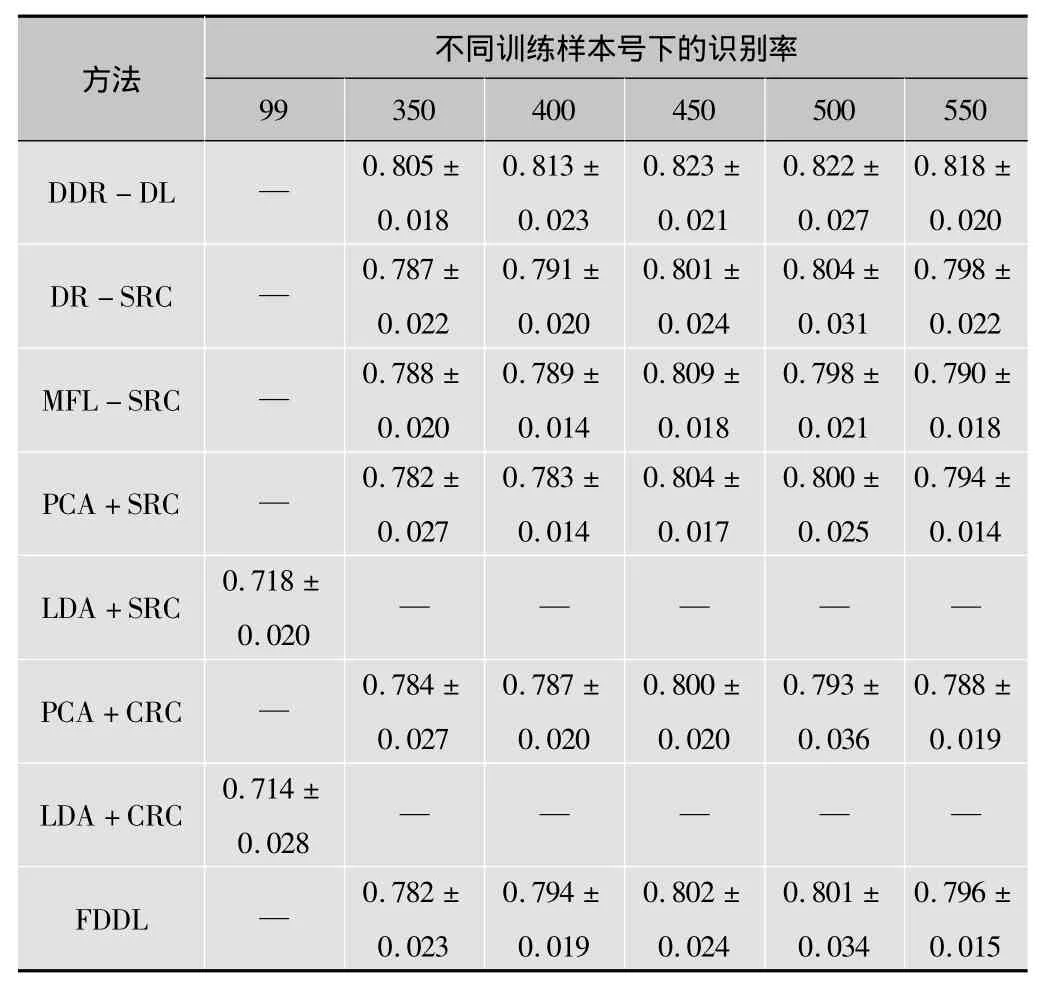
表2 在AR數據庫中不同特征維度的識別率

從表2可以看出，DDR－DL在平均值上優于其他方法，當維度相對較低時，例如350，所有的方法(除了LDA+SRC和LDA+CRC)有相似的結果。隨著特征維度的升高，例如超過450，本文的DDR－DL相對于其他方法表現出了明顯的提高。

2.3 MPIE人臉數據庫

卡內基梅隆大學(Carnegie Mellon University，CMU)的多重PIE數據庫(MPIE)包含4個部分的337個不同對象的人臉圖像，同時涵蓋了表情、光照的變化，實驗選用第一部分的所有249個對象的人臉圖像，圖3所示為MPIE人臉庫的樣本示例。

圖3 MPIE數據庫的樣本示例

實驗從MPIE人臉庫的每個對象中隨機選擇2～7個樣本作為訓練集，其他的圖像作為查詢集，并投影到一個550維的子空間中(方案LDA+SRC和LDA+CRC投影到248維的子空間中)。同樣，所有的實驗重復50次來計算FR率的平均值和標準偏差。表3顯示了不同方法的結果。

從表3可以總結出與AR數據庫相似的結論，即提出的DDR－DL方法實現了最高的識別率，當訓練樣本數不是很充足的時候，相對于其他方法，所提方法的識別效果更佳。

表3 在MPIE數據庫上不同數量訓練樣本的識別率

表4列出了對比方法在不同維度特征上的識別率。隨機取4張人臉圖像用于訓練，剩下的所有圖像用于測試，同樣重復執行50次。

表4 在MPIE數據庫中不同特征維度的識別率

從表4可以得出，與在AR數據庫中觀察的結果相似，隨著維度的增加，相比于其他方法，本文提出的DDRDL方法有明顯改善，同時，LDA+SRC和LDA+CRC在MPIE上有較好的性能，因為所使用的MPIE是含有249個不同類別的大型數據庫，它允許LDA利用足夠多的投影來對查詢樣本進行分類。

2.4 性能分析

為了更好地體現所提方法的優越性，這里分析了所提方法的計算復雜度，包括訓練時間復雜度、測試時間復雜度及空間復雜度，并與其他線性方法進行了比較，比較結果如表5所示，其中，m，n分別表示圖像矩陣的行數和列數，L，M，N分別表示投影向量數、測試樣本數、訓練樣本數。

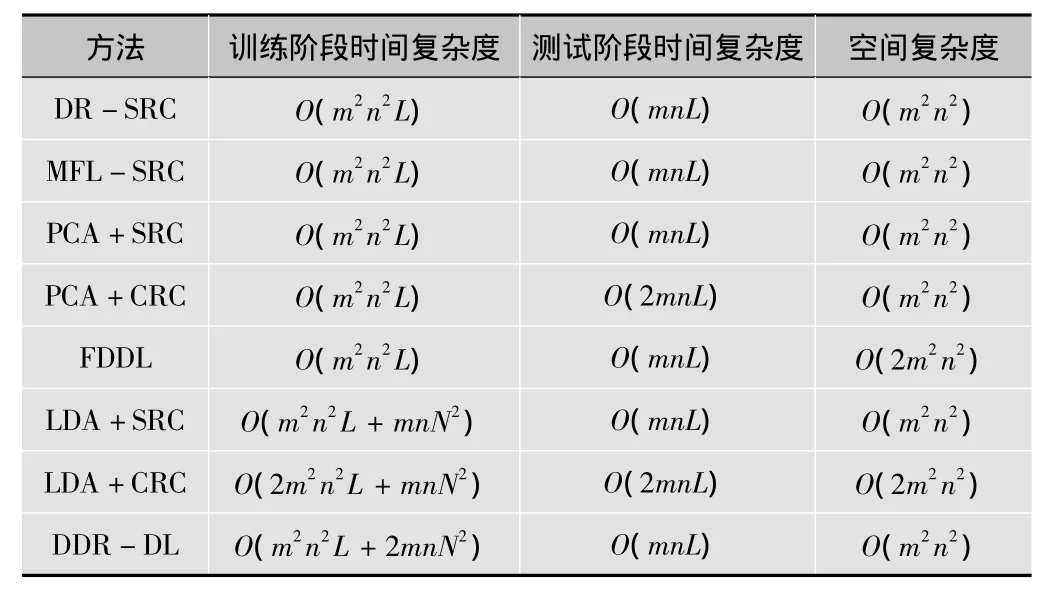
表5 各個方法的時間復雜度比較

從表5可以看出，所提方法在訓練階段的時間復雜度稍高，但是與LDA+CRC、LDA+SRC方法相比還是有明顯的優勢，測試階段的時間復雜度、空間復雜度都不比其他方法遜色，甚至比LDA+CRC方法低得多。

綜上可知，所提方法與 DR-SRC［6］，MFL-SRC［6］，PCA+SRC［7］，PCA+CRC［8］，FDDL［9］，LDA+SRC［10］，LDA+CRC［11］方法相比，雖然在復雜度方面沒有很大的改善，但是在識別率方面有了很大的提高。

3 總結

本文提出了人臉識別中一種基于判別性降維的字典學習(DDR-DL)方法，與很多注意力集中在字典學習(DL)或使用PCA和LDA進行降維(DR)的方法不同，DDR-DL通過將它們耦合進行統一的框架來最小化功率，兼顧了DR和DL處理的相互作用。實驗結果表明，提出的DDR-DL方法優于其他幾種先進的人臉識別方法。

未來會改變不同的初始參數設置，探索更多的參數變化對方法性能的影響，并結合其他的基礎方法，在提高人臉識別率的同時，注重改善識別的效率，以適應現實生活中的實時交互。

:

［1］孫吉貴，劉杰，趙連宇.聚類算法研究［J］.軟件學報，2008，19(1):48-61.

［2］WRIGHT J，YANG A Y，GANESH A，et al.Robust face recognition via sparse representation［J］.IEEE Trans.Pattern Analysis and Machine Intelligence，2009，31(2):210-227.

［3］楊關，馮國燦，陳偉福，等.紋理分析中的圖模型［J］.中國圖象圖形學報，2011，16(10):1818-1825.

［4］HAFIZ F，SHAFIE A A，MUSTAFAH Y M.Face recognition from single sample per person by learning of generic discriminant vectors［J］.Procedia Engineering，2012，45(2):465-472.

［5］喬立山，陳松燦，王敏.基于相關向量機的圖像閾值技術［J］.計算機研究與發展，2010，47(8):1329-1337.

［6］GUANG N，TAO D，LUO Z，et al.Online nonnegative matrix factorization with robust stochastic approximation［J］.IEEE Trans.Neural Networks and Learning Systems，2012，23(7):1087-1099.

［7］王佳奕，葛玉榮.基于Contourlet及支持向量機的紋理識別方法［J］.計算機應用，2013，33(3):677-679.

［8］WRIGHT J，YANG A Y，GANESH A，et al.Robust face recognition via sparse representation［J］.IEEE Trans.Pattern Analysis and Machine Intelligence，2009，31(2):210-227.

［9］ZHANG Z，WANG J，ZHA H.Adaptive manifold learning［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2012，34(1):131-137.

［10］HE R，HU B G，YUAN X T.Robust discriminant analysis based on nonparametric maximum entropy［J］.Advances in Machine Learning，2009，54(3):120-134.

［11］文喬龍，萬遂人，徐雙.Fisher準則和正則化水平集方法分割噪聲圖像［J］.計算機研究與發展，2012，49(6):1339-1347.

［12］ZHONG L W，KWOK J T.Efficient sparse modeling with automatic feature grouping［J］.IEEE Transactions on Neural Networks and Learning Systems，2012，23(9):1436-1447.