基于改進混沌理論和ACPSO-LSSVR的短期負荷預測

孫景文，常鮮戎

(華北電力大學 電氣與電子工程學院，河北 保定 071003)

0 引言

短期負荷預測是負荷預測的重要組成部分，是針對未來一天到數天各時段負荷的研究，對于機組最優組合、經濟調度和最優潮流等有著重要的意義[1]。因此，提高短期負荷預測的精度很有必要。

由于負荷的隨機因素太多，非線性極強，而傳統的負荷預測方法如回歸分析、灰色預測、相似日法等難以達到精度要求。智能算法如神經網絡、支持向量機、模糊粗糙集理論、混沌理論等的出現為負荷預測帶來了新的契機。

支持向量機SVM(Support Vector Machines)是基于Vapnik等提出的統計學習理論，最初用于解決分類問題，隨著不敏感損失函數的引入，開始用于解決回歸問題，即支持向量回歸機SVR(Support Vector Regression)。SVR已經廣泛應用于時間序列預測領域[2，3]，當然也包括電力負荷預測領域[4，5]。由于基本的 SVR需要求解的是二次規劃問題，數據樣本較大時求解比較慢，因此實用階段受到了一定的限制。最小二乘支持向量機LSSVR(Least Square Support Vector Regression)[6]將SVR中的損失函數設定為最小二乘損失函數，將不等式約束轉化為等式約束，從而使得問題求解變成線性KKT(Karush-Kuhn-Tucker)方程組的求解，求解速度很快。LSSVR用于負荷預測有兩個關鍵因素:(1)訓練樣本即輸入輸出選取;(2)LSSVR的正則化參數和核函數參數選取。

針對關鍵因素 (1)，本文擬采用改進混沌理論解決。通過求解最大李雅普諾夫指數可以判斷電力負荷序列屬于混沌序列[7]，因此可以用重構相空間理論將一維負荷序列映射到高維空間中去。SVR的核心思想正是利用核函數將低維輸入映射到高維空間，與混沌理論有相似之處。文獻[7]和[8]都指出，數值測試表明，按照經典混沌理論選擇的嵌入維數和延遲時間一般都不是負荷預測需要的合適參數。因此，有必要尋找合適的方法來進行參數優選。

針對關鍵因素 (2)，本文擬采用ACPSO(A-daptive Chaos Particle Swarm Optimization)來解決。LSSVR的參數選擇對于預測的精度來說非常重要，因此必須進行認真精確的尋找。文獻[9]采用交叉驗證的思想進行最優參數的選取，但是效率不高;文獻[10]采用粒子群算法進行參數優化，但基本的粒子群算法易陷入局部極小，搜索后期速度緩慢，效果也不甚理想。ACPSO是基本PSO的改進算法，針對PSO的缺點，引入自適應策略和混沌思想，有效提高PSO的算法性能。

因此，為了提高短期負荷預測的精度和速度，本文提出了基于改進混沌理論和ACPSO-LSSVR的預測模型。首先利用改進混沌理論優選LSSVR的訓練樣本即輸入輸出，然后利用ACPSO優選LSSVR的參數，最后利用LSSVR進行快速的負荷預測。實例分析驗證了該方法的有效性。

1 改進混沌理論

重構相空間過程中，嵌入維數m、延遲時間τ和預測參考點的正確選取是重構成功的關鍵。

1.1 嵌入維數和延遲時間的選取

關于嵌入維數和延遲時間的選取，已經有很多成熟的理論方法，如G-P法、偽最近鄰域法、真實矢量場法和Cao氏法確定嵌入維數;自相關法、改進自相關法和互信息法確定延遲時間[11]。上述方法均是將二者的求取獨立計算，而近年來學者指出影響重構質量的是嵌入窗寬，即 (m-1)τ。基于此，kim，Eykholt和Salas提出C-C方法[12]，如下:

將原始時間序列x(i)，i=1，2，…，N分成t個不相交的子序列，長度l=[N/t]([]表示取整):

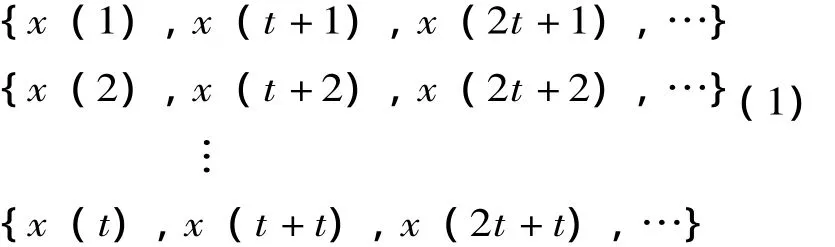
計算每個子序列的統計量S(m，N，r，τ):

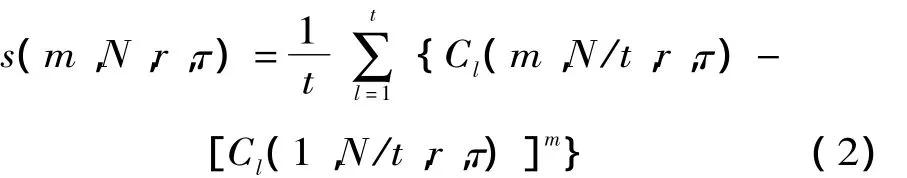
式中:Cl是第l個子序列的關聯積分，定義如式(3):

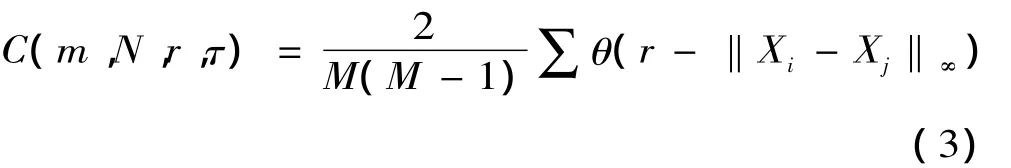
局部最大間隔可以取S的零點或對所有的半徑r相互差別最小的時間點。定義差量如式 (4):

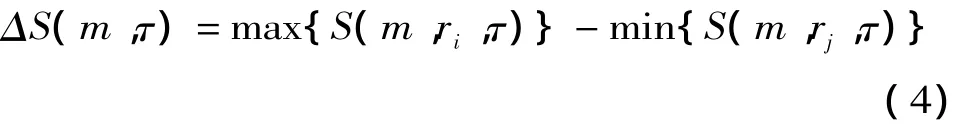
根據統計學原理，m取值在2～5之間，r取值在σ/2～2σ之間。σ是時間序列的均方差。得到方程如式 (5):

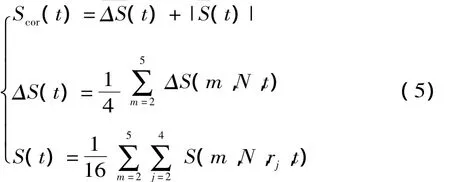
傳統C-C法認為S(t)的第一個過零點或ΔS(t)的第一個極小點就是最優延遲時間τ，Scor(t)的全局最小點就是嵌入窗寬τw。

以Lorenzs混沌系統為例，得到C-C法確定的m，τ和τw如表1。由表1可以看出，S(t)的第一個零點與ΔS(t)的第一個極小點一般不相等，得出的延遲時間相差很多，并且S(t)的第一個零點確定的延遲時間不穩定。同時，Scor(t)曲線上 (限于篇幅，此處略去)存在一些與最小點很接近的局部極小點，它們的存在對于尋找最小點很不利[13]。

表1 C-C法確定洛倫茲混沌序列

鑒于C-C法存在的不足，本文作出如下改進:(1)由于ΔS(t)確定的延遲時間很穩定，僅以其作為延遲時間的選擇依據;(2)定義S1(m，τ)=std{S(m，r，τ)}，這比采用公式 (4)可以更全面衡量全部相點的均勻性。定義Scor2(t)=S1(t)+|S(t)|，發現其一般有比較明顯的周期性，因此，以Scor2(t)的周期作為嵌入窗寬。用改進方法求Lorenz序列的m，τ和τw如表2。

1.2 鄰近相點的選取

混沌預測方法包括全局預測和局域預測。全局預測需要滿足所有訓練相點，這導致了其高度復雜性，很難實用。因此，本文選擇局域預測法。但是，局域預測需要尋找與待預測相點鄰近的若干相點，來擬合非線性函數。因此，鄰近相點的選取至關重要。

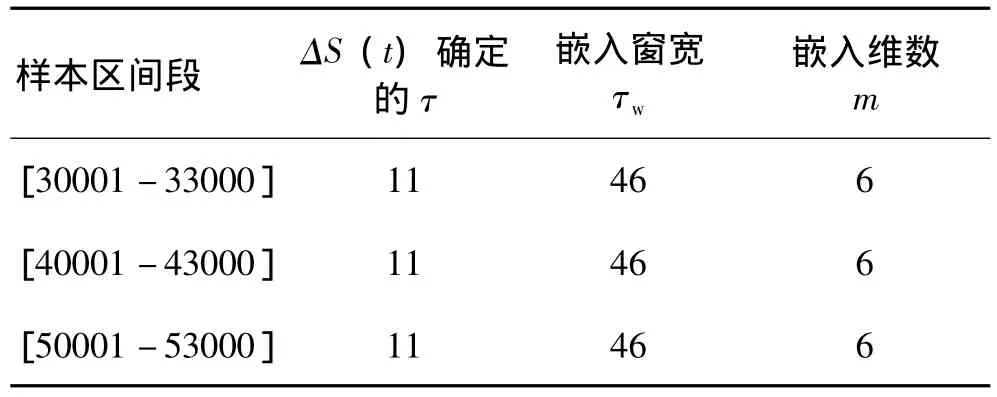
表2 改進C-C法確定洛倫茲混沌序列

多數選取方法是依據相點間的歐氏距離來衡量鄰近程度，即用各相點與預測中心點的歐式距離大小來選取鄰近點，但這種做法很容易引進“偽鄰近相點”，即當前距離接近，并不意味著相點的演化趨勢接近，因此應該以歐氏距離和相點演化趨勢兩個標準進行衡量。方法如下:

(1)依據歐式距離尋找與預測中心點XM接近的K個待優選的初始鄰近相點Xi1(i=1，2，…，k);

(2)向前追蹤K個待優選的初始鄰近相點的歷史情況，本文選擇追蹤兩步，看是否與預測中心相點在演化過程“一直鄰近”，若出現不鄰近情況，則認為該鄰近相點是偽鄰近點，剔除;

(3)經過 (1)和 (2)保留下來的相點才是真正的鄰近相點，以它們作為訓練樣本。

2 最小二乘支持向量機LSSVR

LSSVR不同于標準SVR在于它把不等式約束變成等式約束，并且將經驗風險由偏差的一次方變為二次方，將求解二次規劃問題轉化為求解線性方程組的問題。

對于給定的訓練樣本集 (xi，yi)，i=1，…，l，xi∈Rn，yi∈R，利用高維空間里的線性函數來擬合:

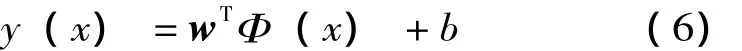
式中:Φ()代表非線性映射。把數據樣本從輸入空間映射到高維特征空間，使輸入空間中的非線性擬合問題變為高維空間中的線性擬合問題。根據結構風險最小化原理，綜合考慮擬合誤差和函數復雜度，回歸問題可以表示為約束優化問題:

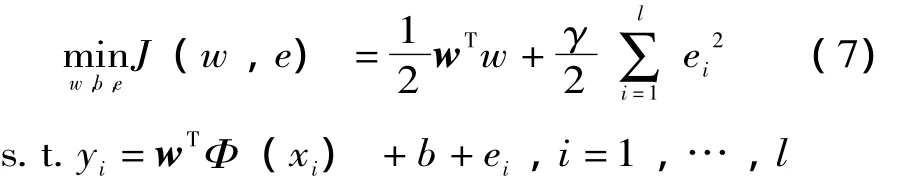
式中:γ為正則化參數;b為偏差。為了求解

(7)式的優化問題，將有約束優化問題轉化為無約束優化問題，建立下述Lagrange函數:

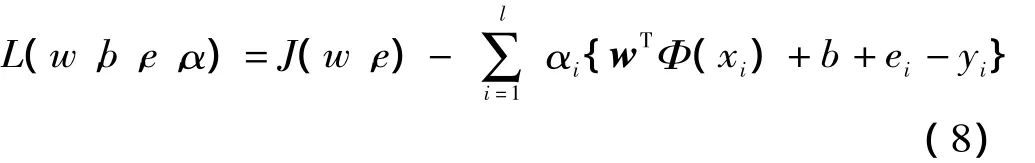
式中:αi是 Lagrange乘子，根據 Karush-Kuhn-Tucker最優條件，消去ei和w后，得到如下線性方程組:

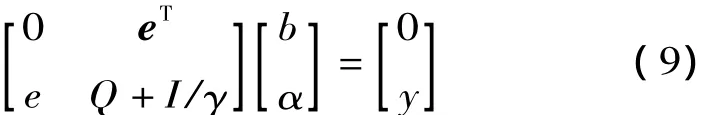
求解式 (9)可以得到b和α，最后可得如下預測模型:

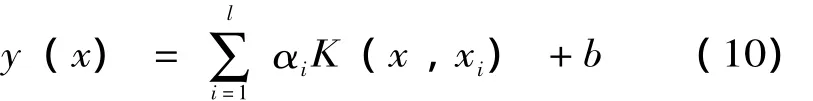
由上可知，LSSVR具有更小的計算復雜度，并且需要確定的參數僅有兩個γ和σ。

3 自適應混沌粒子群算法ACPSO

粒子群算法是由美國心理學家Kennedy和電氣工程師Eberhart于1995年提出的一種模擬鳥類群體覓食行為的仿生智能算法，是基于群體智能的隨機尋優算法[14]。

3.1 標準粒子群PSO

假設在D維的搜索空間，有一群體，其粒子數為m，xi=(xi1，xi2，…，xiD)表示第i個粒子的位置，vi= (vi1，vi2，…，viD)表示第i個粒子的飛行速度，Pi= (pi1，pi2，…，piD)表示第 i個粒子經歷過的最好位置，即適應度值最優，Pg=(pg1，pg2，…，pgD)表示所有粒子經歷過的最好位置。每次迭代粒子根據下面公式更新自己的速度和位置:

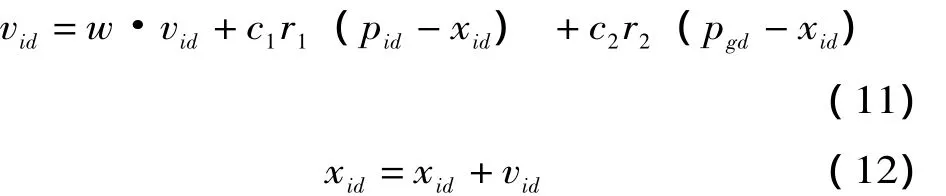
式 (11)中:w表示慣性權重，取0.1-0.9;c1和c2表示學習因子，一般均取2;r1和r2是[0，1]之間隨機數。公式由3部分組成，第一部分是粒子之前的速度;第二部分是“認知”部分，代表粒子本身的思考，僅考慮自身的經驗;第三部分是“社會”部分，代表著粒子之間的社會信息共享。

粒子在搜索過程中，速度和位置都有一定的限制，即 vimin≤vi≤vimax，ximin≤xi≤ximax，如果超出，就取邊界值。

3.2 混沌粒子群CPSO

3.1中提出的基本PSO，其搜索過程有兩點明顯不足:(1)初始化粒子是隨機的，隨機過程雖然大多能保證粒子初始分布較均勻，但對于粒子質量卻不能保證，影響收斂;(2)迭代過程中，當粒子位置、個體極值和群體極值3個接近時，速度更新由wvid決定。由于w＜1，粒子速度越來越慢，接近于零，失去全局搜索能力，最后導致陷入局部極小。

一般來說，由確定性方程得到的具有隨機性的運動狀態叫做混沌。混沌具有隨機性和遍歷性。將混沌思想引入PSO主要體現在兩個方面:(1)采用混沌序列初始化粒子的位置和速度，從中擇優選取初始群體;(2)以當前群體搜索到的最優位置為基礎產生混沌序列，以混沌序列中的最優位置粒子取代群體中任一個粒子的位置。

一般以Logistic方程確定的混沌系統對PSO進行改進，方程為

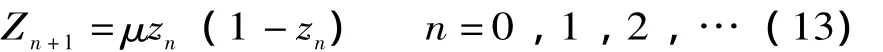
μ為控制參數，建議取4，初值z0∈[0，1]，具體的改進過程參見文獻[15]。

3.3 自適應粒子群APSO

在標準PSO中，w對于算法收斂有重要影響:w值大有利于全局搜索，有利于保持粒子多樣性;w值小有利于局部搜索，粒子多樣性逐漸喪失。保持群體多樣性是算法能夠收斂到全局最優的前提，而標準PSO的迭代是多樣性逐漸喪失的過程，因此本文提出自適應調整w的改進方法。

假設群體規模是m，若favg是粒子當前適應度平均值，則

式中:fi是第i個粒子的當前適應度值。設最優粒子適應度值為fg，并且將適應度值優于favg的粒子再次求平均得到favg1。由此可將群體根據適應度值差異分為3個子群，分別采用不同的自適應操作，使群體始終保持多樣性。w小的粒子用來局部尋優，加速收斂;w大的粒子早期用來全局尋優，后期用來跳出局部極小，避免早熟收斂。

適應度值為fi的粒子，w調整如下:

(1)fi優于favg1:該粒子已接近全局最優，所以應被賦予較小w，加速向全局最優收斂，公式如下:

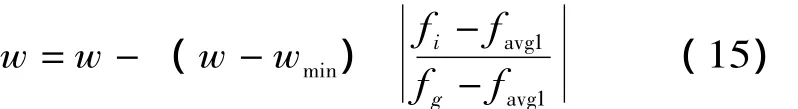
(2)fi優于favg但次于favg1:該粒子是群體中一般的粒子，具有良好的全局尋優和局部尋優能力，以遞減策略進行調整:

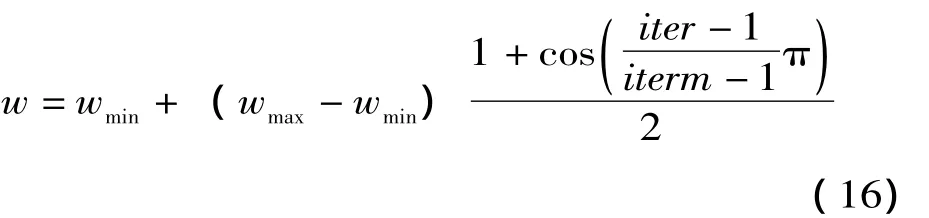
(3)fi次于favg:該粒子是群體中較差的粒子，w的調整參考文獻[16]來進行:

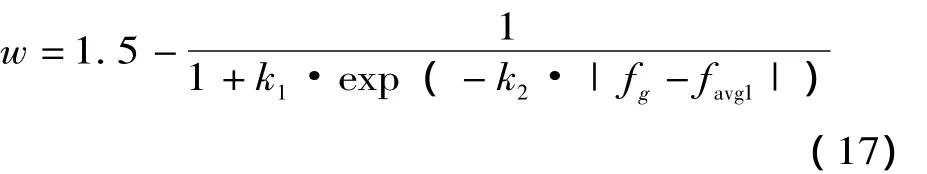
算法停滯時，如果粒子分布分散，則|fgfavg1|較大，式 (17)中w會減小，加強局部尋優;如果粒子分布密集，則|fg-favg1|較小，式(17)中w會增大，粒子全局尋優能力加強，有效跳出局部最優。

3.4 ACPSO算法流程

ACPSO是將混沌思想和自適應思想融合進標準PSO中產生的改進算法，流程如下:

Step1:初始化最大迭代次數iterm，群體規模m，位置和速度的上下限，終止閾值ε，混沌初始化粒子的位置和速度;

Step2:計算粒子適應度值fi，若fi優于Pi的適應度值，則替換Pi;若fi優于Pg的適應度值，則替換Pg;

Step3:根據公式 (11)、(12)更新粒子的位置和速度;

Step4:對最優位置Pg進行混沌優化，得到性能最好的可行解，替換任一粒子;

Step5:判斷終止條件是否滿足。滿足轉向Step7，否則轉向Step6;

Step6:根據粒子適應度值采取相應的w調整策略，按照式 (15)、(16)、(17);

Step7:滿足終止條件，算法結束。

4 算例分析

本文以2001年歐洲智能技術網絡舉辦的關于電力負荷預測技術大賽的原始數據為例，檢驗本文所提出方法的有效性。

原始數據為1997年和1998年兩年的每30 min一次的電力負荷值。本文選取1998年1月1日至1998年3月31日的電力負荷進行驗證。其中1月1日至2月28日負荷作為訓練樣本，3月1日至3月24日為檢測樣本，3月25日至3月31日為待預測樣本。

4.1 嵌入維數和延遲時間的確定

對于實際的電力負荷來說，預測之前首先要做的工作就是判斷其是否為混沌序列。最大李雅普諾夫指數一般用來進行混沌的判別，混沌序列的最大李雅普諾夫指數大于零。通過采用小數據量法[11]對實際電力負荷進行判別，其最大李雅普諾夫指數為0.023。

通過采用改進的C-C法進行嵌入維數和延遲時間的選取，得到m=4，τ=16，τw=48。文獻[7]指出，對于24 h的負荷序列來說，τ=8在數值測試中誤差相對較小，而對于本文中48 h的負荷序列，正好是 τ=16，很吻合。文獻[8]指出，嵌入窗寬τw不應該是 (m-1)τ，而應該是(m+1)τ/3。因此，本文固定τ=16不變，將m取值限定為3～10，以測試樣本預測誤差為衡量標準，選擇最優的m。結果如表3，mse表示平均誤差。

表3 不同m對應的測試誤差

4.2 鄰近相點的選取

本文采用1.2節提出的選取方法對鄰近相點進行選取:首先確定用于局域預測的鄰近相點的個數，鄰近相點個數太少不利于規律的尋找，而鄰近相點的個數太多又會導致訓練時間的增加，并且使得一些偽鄰近相點進入到訓練樣本中，影響預測的精度。本文根據文獻[17]中采用的HQ準則 (Hannan-Quinn準則，即漢南-奎因準則)進行鄰近相點個數的確定，得出鄰近相點個數為30。然后，本文先將鄰近相點個數確定為50個，即“粗選取”，追蹤這50個相點的演化軌跡，根據歐式距離和演化情況選取其中最優的30個，即“細選取”。最后，以這30個相點作為訓練樣本對SVR進行訓練，對待預測點進行預測。

4.3 基于ACPSO-LSSVR的預測

由于需要預測未來24 h即48點的負荷，預測分為單步遞歸預測和多步預測兩種方式。本文采用單步遞歸預測，即每次預測一個點，然后將該預測點作為已知負荷加入到序列中，預測下一個點，以此類推，直至48個點全部預測完畢。

本文采用ACPSO進行SVR參數優選時，懲罰因子γ/2限定范圍是[1，500]，核函數寬度2σ2的限定范圍是[0.01，10]。

為了更直觀地說明預測效果，本文將3月25日至3月31日的待預測樣本每天的預測均方誤差mse，單點最大預測誤差max和單點最小誤差min統計如表4。將3月25日的每點預測情況作圖如圖1。

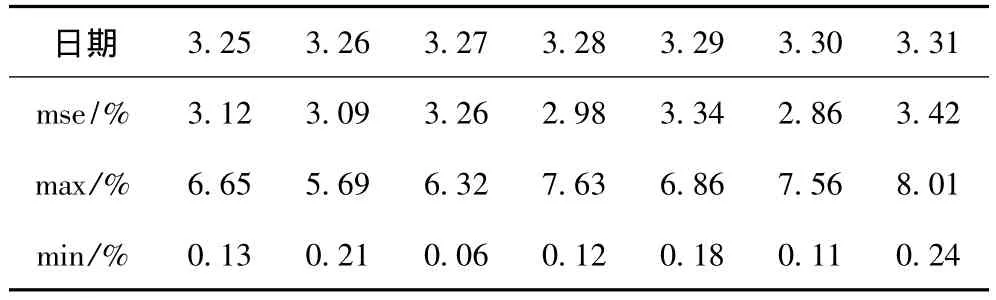
表4 3月25日至3月31日預測誤差

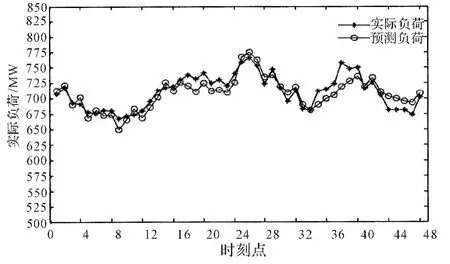
圖1 3月25日每點預測情況

為了說明本文提出的方法的有效性和改進效果。本文分別以網格搜索法確定最優參數的LSSVR方法 (簡稱LSSVR)，以標準PSO確定最優參數的LSSVR方法 (簡稱PSO-LSSVR)，以ACPSO確定最優參數的傳統SVR方法 (簡稱ACPSOSVR)分別對同樣的電力負荷進行預測，從精度和速度兩個方面進行比較，結果如表5。

由表5可以看出，本文提出方法不論是預測精度還是預測速度都有優勢。比較預測精度可以看出，采用ACPSO優化參數之后，精度能夠得到提高，二者預測精度比用網格搜索法和標準PSO的預測模型精度要高。比較預測時間可以看出，除了網格搜索法的LSSVR(因為網格搜索要進行大量的重復試探性計算)，采用LSSVR比采用SVR所耗費的時間少很多，驗證了采用LSSVR提高計算速度的可行性;而采用LSSVR的預測方法中，ACPSO所用的預測時間最短，驗證了采用優化算法優化參數的可行性。

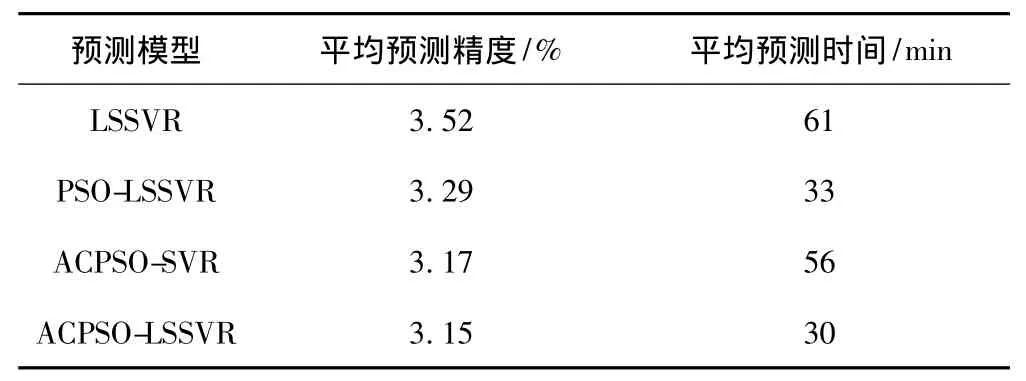
表5 4種不同預測方法比較

5 結論

本文針對目前常用的混沌理論存在的相空間重構不準確以及鄰近點選擇不準確的缺點，提出了改進C-C法進行相空間重構和追蹤鄰近相點演化軌跡排除“偽鄰近點”的改進混沌理論;針對傳統的SVR求解速度慢以及參數難以確定的缺點，提出采用LSSVR加快求解速度和ACPSO確定最優參數的ACPSO-LSSVR。對于實際負荷的預測分析證明了該方法的有效性和實用性。但是，目前對于負荷預測的精度和速度要求甚高，如何進一步提高預測精度和預測速度仍然是負荷預測的關鍵問題和難題。

[1]康重慶，夏清，劉梅.電力系統負荷預測[M].北京:中國電力出版社，2007.

[2]崔萬照，朱長純，保文星，等.混沌時間序列的支持向量機預測[J].物理學報，2004，53(10):3303-3310.

[3]謝宏，魏江平，劉鶴立.短期負荷預測中支持向量機模型的參數選取和優化方法[J].中國電機工程學報，2006，26(22):17-22.

[4]陸寧，武本令，劉穎.基于自適應粒子群優化的SVM模型在負荷預測中的應用[J].電力系統保護與控制，2011，39(15):43-47.

[5]王奔，冷北雪，張喜海，等.支持向量機在短期負荷預測中的應用概況[J].電力系統及其自動化學報，2011，23(4):115-121.

[6]唐杰明，劉俊勇，楊可，等.基于灰色模型和最小二乘支持向量機的電力短期負荷組合預測[J].電網技術，2009，33(3):63-68.

[7]楊正瓴，林孔元.短期負荷預測相空間重構法參數優選的數值測試與分析[J].電力系統自動化，2003，27(16):40-44.

[8]谷子，唐巍.電力短期負荷時間序列混沌相空間重構參數優選法[J].中國電機工程學報，2006，26(14):18-23.

[9]李元誠，方廷健，于爾鏗.短期負荷預測的支持向量機方法研究[J].中國電機工程學報，2003，23(6):55-59.

[10]李文元，閆海華，姚宏杰.粒子群優化的最小二乘支持向量機在通信裝備故障預測中的應用[J].微電子學與計算機，2013，30(2):99-102.

[11]韓敏.混沌時間序列預測理論與方法[M].北京:中國水利水電出版社，2007.

[12]Kim H S，Eykholt R，Salas J D.Nonlinear dynamics，delay times，and embedding windows[J].Physical D，1999，12:48-60.

[13]陸振波，蔡志明，姜可宇.基于改進的C-C方法的相空間重構參數選擇[J].系統仿真學報，2007，19(11):2527-2530.

[14]段海濱，張祥銀，徐春芳.仿生智能計算[M].北京:科學出版社，2011.

[15]高鷹，謝勝利.混沌粒子群優化算法[J].計算機科學，2004，31(8):13-15.

[16]吳浩揚，朱長純，常炳國，等.基于種群過早收斂程度定量分析的改進自適應遺傳算法[J].西安交通大學學報，1999，33(11):27-31.

[17]高俊杰.混沌時間序列預測研究及應用[D].上海:上海交通大學，2013.

[18]何洋，鄒波，李文君，等.基于混沌理論的電力系統短期負荷預測的局域模型[J].華北電力大學學報，2013，40(4):43-50.

[19]朱麗仙，苑津莎，張英慧.基于粗糙集和支持向量機的電力系統短期負荷預測[J].電力科學與工程，2010，26(2):32-35.