誤差修正機制轉(zhuǎn)換模型的貝葉斯估計

丁 輝，王咪咪

(滁州學(xué)院 數(shù)學(xué)科學(xué)學(xué)院，安徽 滁州 239000)

0 引言

誤差修正模型(ECM)既能描述不同時間序列變量之間的長期均衡關(guān)系，又能反映出時間序列變量間的短期非均衡關(guān)系向長期均衡關(guān)系修正的機制，是分析時間序列變量之間長期和短期綜合影響的一個強有力的工具。然而在現(xiàn)實經(jīng)濟實體中，由于市場上存在著交易費用與經(jīng)濟政策的突變，導(dǎo)致時間序列變量之間的長期均衡關(guān)系并不是一直都存在，發(fā)生了結(jié)構(gòu)機制上的突變。而針對結(jié)構(gòu)機制上的突變這種現(xiàn)象，Hamilton［1］提出了馬爾科夫機制轉(zhuǎn)換模型(MS模型)。該模型可以有效地描述經(jīng)濟變量在不同機制下的行為特征。因此將馬爾科夫轉(zhuǎn)換機制引入到誤差修正模型中，便形成了誤差修正機制轉(zhuǎn)換模型(簡稱MSECM)。該模型既有效地描述了變量之間的長期和短期綜合關(guān)系，又解決了現(xiàn)實經(jīng)濟實體中協(xié)整關(guān)系的機制改變難題，因此在經(jīng)濟領(lǐng)域中得到了廣泛的應(yīng)用。

到目前為止，關(guān)于誤差修正機制轉(zhuǎn)換模型甚至馬爾科夫機制轉(zhuǎn)換模型的參數(shù)估計方法主要是極大似然估計法或者近似極大似然估計法［2］。極大似然估計方法屬于經(jīng)典估計方法，并沒有結(jié)合樣本數(shù)據(jù)的先驗信息。而貝葉斯估計法相對于經(jīng)典估計，結(jié)合了數(shù)據(jù)的信息與參數(shù)的先驗信息，而且還能對缺失數(shù)據(jù)、截尾數(shù)據(jù)等進行簡明化處理，因此相對與其他經(jīng)典估計具有無與倫比的優(yōu)勢。下面將使用貝葉斯估計法來估計誤差修正機制轉(zhuǎn)換模型中的未知參數(shù)。

1 誤差修正機制轉(zhuǎn)換模型及其相關(guān)概念

假設(shè){xt}、{yt} 是兩個一階單整時間序列，即xt～I(1)，yt～I(1)。并設(shè)x1，x2，…，xn;y1，y2，…，yn分別為這兩個序列的觀測值。誤差修正機制轉(zhuǎn)換模型的形式如下:

當(dāng)xt、yt之間存在協(xié)整關(guān)系時，則xt、yt滿足誤差修正模型，即:

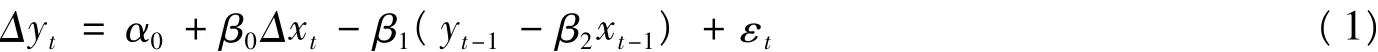
其中ecm=yt-1-β2xt-1為誤差修正項，Δyt=yt-yt-1，Δxt=xt-xt-1，隨機誤差項εt是一個白噪聲過程，它們相互獨立，且都服從正態(tài)分布N(0，σ2)。

當(dāng)xt、yt之間不存在協(xié)整關(guān)系時，則xt、yt不存在長期均衡關(guān)系，即β1=0，模型變?yōu)?/p>

為了簡化誤差修正機制轉(zhuǎn)換模型的形式，引入機制變量st，當(dāng)st=1時表示xt、yt存在協(xié)整關(guān)系，當(dāng)st=0時表示xt、yt不存在協(xié)整關(guān)系，且機制變量st滿足:

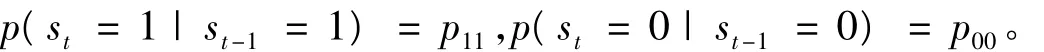
于是誤差修正機制轉(zhuǎn)換模型的一般形式表達如下:

其中 εt～ N(0，σ2)。

2 誤差修正機制轉(zhuǎn)換模型的貝葉斯估計

2.1 模型簡化

為了對該模型應(yīng)用貝葉斯估計，對該模型進行進一步的簡化。令

則模型簡化為:

2.2 參數(shù)的先驗分布

為了消除信息不準確時先驗分布對貝葉斯估計帶來的估計影響，采取無信息先驗分布［3］。

假設(shè)參數(shù)β服從均勻分布，即f(β)∝1;

參數(shù)σ2服從均勻分布，即f(σ2)∝1;

參數(shù)p11服從均勻分布U(0，1)，即f(p11)∝1;

參數(shù)p00服從均勻分布U(0，1)，即f(p00)∝1。

2.3 模型的似然函數(shù)

模型(4)的似然函數(shù)為

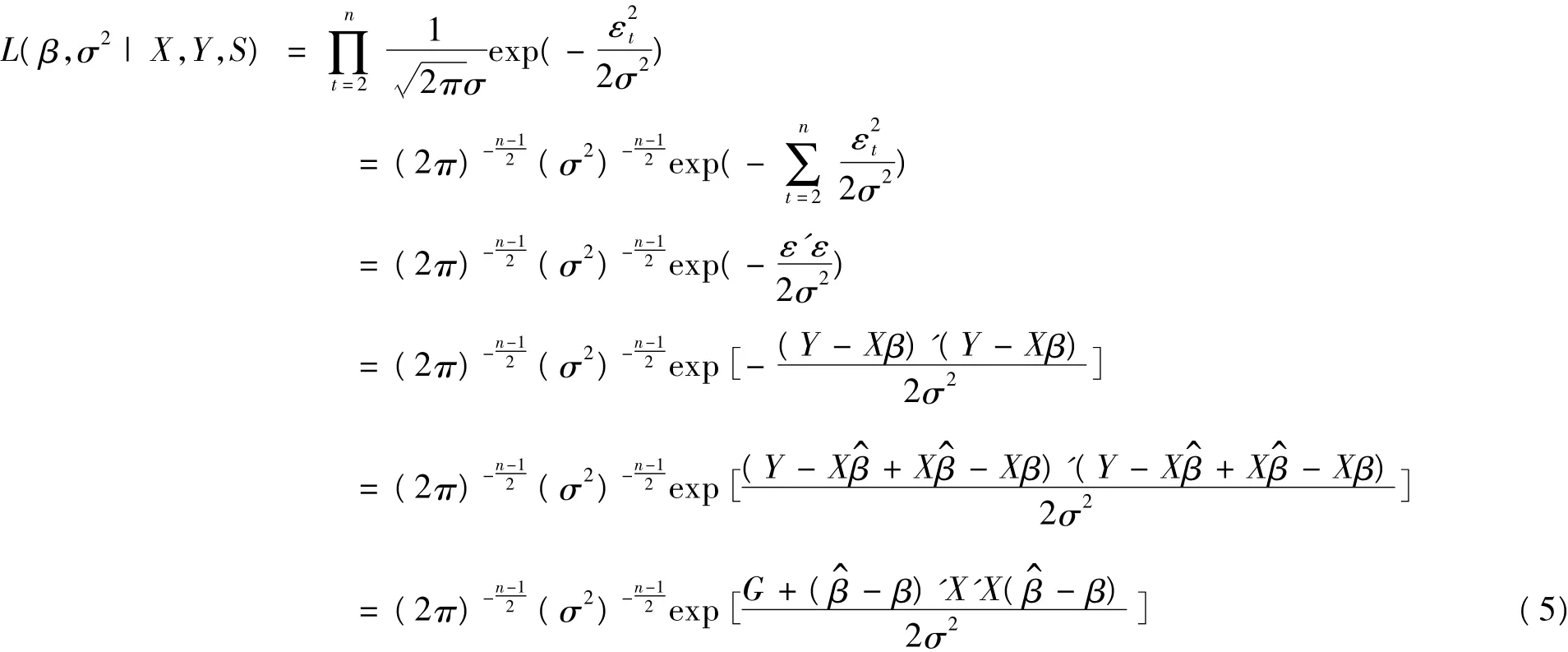
2.4 參數(shù)的后驗分布

機制變量S的分量之間高度相關(guān)，因此若使用滿條件后驗分布去實現(xiàn)機制變量S的估計是無效的［4］。為此，采用 Frühwirth-Schnatter［5］和 Carter、Kohn［6］提出的 FFBS 算法來實現(xiàn)機制變量 S 的估計。

令 Xt=(x1，x2，…，xt)'，Yt=(y1，y2，…，yt)'，則由貝葉斯定理可知

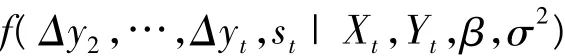
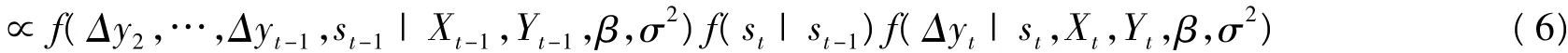
FFBS具體算法:首先計算pn(0)，并從均勻分布U(0，1)中產(chǎn)生隨機數(shù)，若該隨機數(shù)小于pn(0)，則sn=0，否則sn=1;然后根據(jù)(7)式得到的概率，按照完全相同的方法從后往前依次抽取sn-1，sn-2，…，s1，即得到機制變量S的抽樣。

機制變量S求出后，則有β，σ2的聯(lián)合后驗分布為

對(8)式關(guān)于β積分，得σ2的后驗分布為

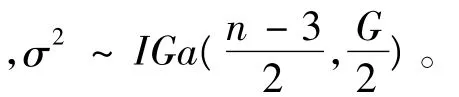
對(8)式關(guān)于σ2積分，得β的后驗分布

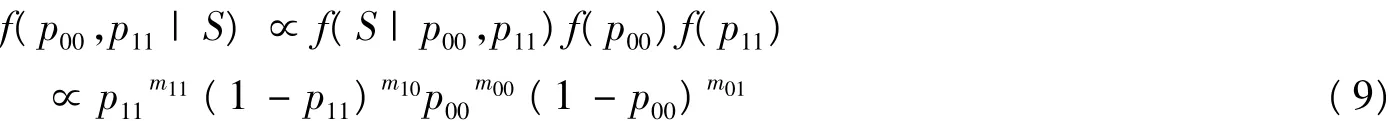
其中mij(i=0，1;j=0，1)表示機制變量st從機制i變化到機制j的次數(shù)。

對(9)式關(guān)于p00積分，得p11的后驗分布

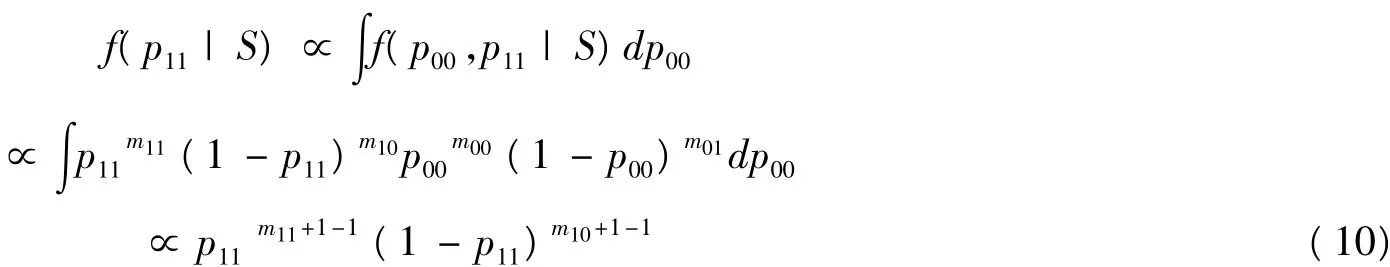
即參數(shù)p11服從Beta分布，p11～beta(m11+1，m10+1)。

對(9)式關(guān)于p11積分，得p00的后驗分布

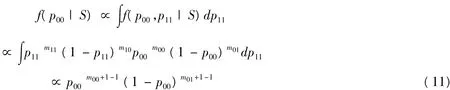
即參數(shù)p00服從Beta分布，p00～beta(m00+1，m01+1)。

至此，模型中各個參數(shù)的后驗分布均已求出，因此可以使用基于Gibbs抽樣的貝葉斯估計技術(shù)［7］對模型進行參數(shù)估計。現(xiàn)將該模型貝葉斯估計的算法說明如下:

Step1:給定 β，σ2的初值 β(0)，σ2(0)，令i=1。

Step 2:使用FFBS抽樣算法抽取狀態(tài)變量S(i)。

Step 5:從beta(m11+1，m10+1)抽取參數(shù)

Step 6:從beta(m00+1，m01+1)抽取參數(shù)

Step 7:令i=i+1，回到步驟3。

將Step 2至Step 7運行T次，直至參數(shù)估計的馬氏鏈收斂為止，并且將參數(shù)估計的前M次取值舍去，用以消除參數(shù)初值對估計造成的影響。

3 統(tǒng)計模擬

為了測試誤差修正機制轉(zhuǎn)換模型的貝葉斯估計方法的性能，設(shè)定模型如下:

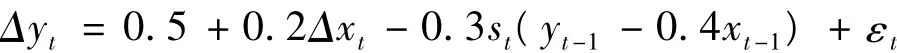
其中 εt～N(0，0.01)，p00=0.93，p11=0.96。

使用統(tǒng)計軟件隨機生成了500組上述模型的時間序列數(shù)據(jù)，接著對該時間序列數(shù)據(jù)應(yīng)用上述貝葉斯估計方法進行估計，一共迭代10000次，接著刪除前面的2000次數(shù)值，用以消除初值對參數(shù)估計的影響，得到各個參數(shù)估計的圖(由于篇幅限制，這里僅給出S、α0、β0的參數(shù)估計圖)。

由圖1、圖2可以看出機制變量S的真實值與S的估計值除去幾個個別值之外估計非常準確，估計效果較好。

由圖3、圖4可以看出可以α0、β0及其他參數(shù)的參數(shù)估計值均已收斂，接著進一步求出各個參數(shù)估計結(jié)果，如表1所示:

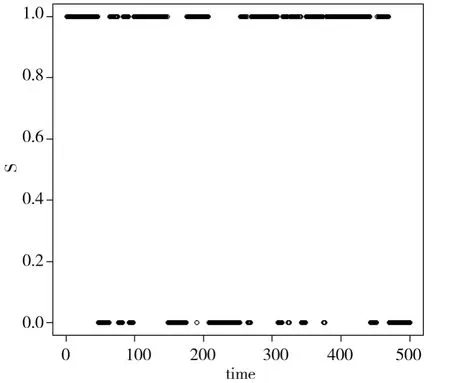
圖1 機制變量S的真實值

圖2 機制變量S的估計值

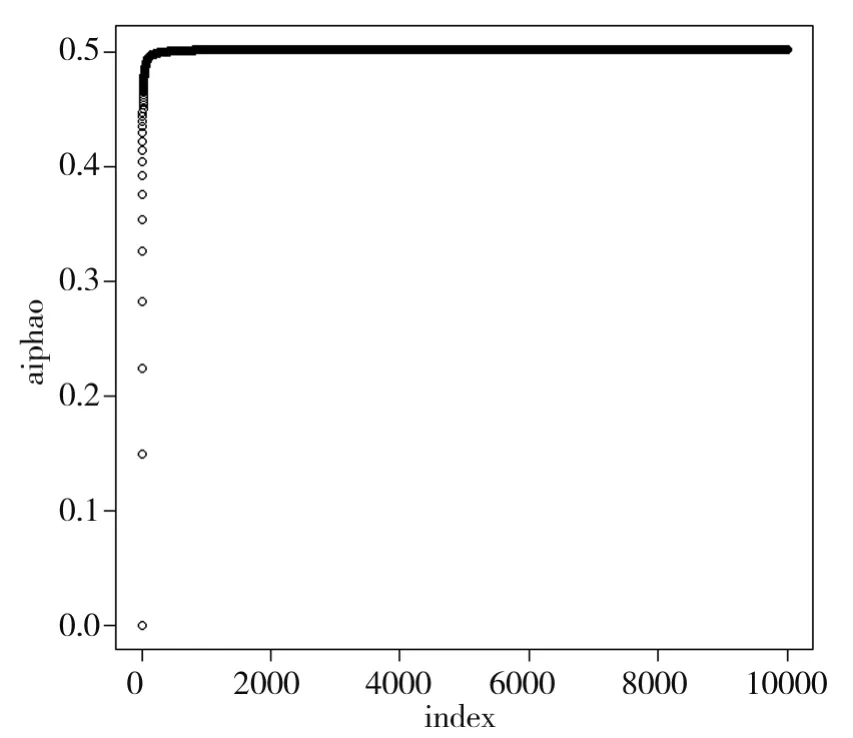
圖3 變量α0的估計值

圖4 變量β0的估計值

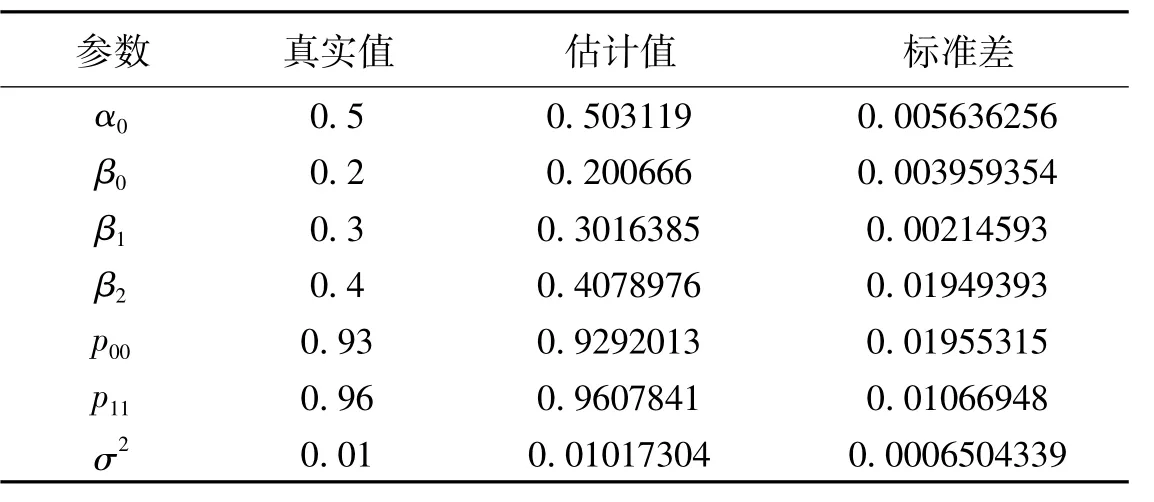
表1 誤差修正機制轉(zhuǎn)換模型的參數(shù)估計

由表1可以看出，使用的貝葉斯估計法可以穩(wěn)健的估計出誤差修正機制轉(zhuǎn)換模型的參數(shù)，該貝葉斯估計方法是可靠的。

4 結(jié)論

誤差修正機制轉(zhuǎn)換模型是金融時間序列模型中應(yīng)用較為廣泛的一類。不同于經(jīng)典的極大似然估計方法，通過無信息先驗分布的設(shè)定，借助于FFBS算法和貝葉斯定理求出各個未知參數(shù)的后驗分布，并且使用基于Gibbs抽樣的貝葉斯估計技術(shù)實現(xiàn)了參數(shù)估計，由統(tǒng)計模擬的效果來看，該方法估計效果較好，對于今后機制轉(zhuǎn)換模型的深入討論提供了重要的參考工具。

［1］Hamilton.A New Approach to the Economic Analysis of Nonstationary Time Series and the Business Cycle［J］.Econometrica，1989，57(2):357-384.

［2］原子霞，楊政.馬爾科夫協(xié)整回歸模型的動態(tài)濾波估計［J］.控制理論與應(yīng)用，2013，30(3):360-364.

［3］鄒鯤，廖桂生，李軍.等.基于Bayes框架的復(fù)合高斯雜波下穩(wěn)健檢測［J］.電子與信息學(xué)報，2013(7):1555-1561.

［4］G.E.B.Archer and D.M.Titterington.Parameter Estimation for Hidden Markov Chains［J］.Journal of Statistical Planning and inference，2002，108(1):365-390.

［5］Frühwirth-Schnatter.Data augmentation and dynamic linear models［J］.Journal of Time Series Analysis，1994，15(2):183-202.

［6］Carter，Chris，Robert Kohn.On Gibbs sampling for state space models［J］.Biometrika，1994，81(3):541-553.

［7］茆詩松，王靜龍，濮曉龍.高等數(shù)理統(tǒng)計［M］.2版.北京:高等教育出版社，2006.