具有未知死區(qū)的SⅠSO非仿射非線性系統(tǒng)間接自適應(yīng)模糊控制

周衛(wèi)東，廖成毅，鄭 蘭，程 華

(1.哈爾濱工程大學(xué)自動(dòng)化學(xué)院，150001哈爾濱;2.齊齊哈爾市建華機(jī)械有限公司，161006黑龍江 齊齊哈爾)

在工業(yè)過(guò)程中經(jīng)常遇到死區(qū)現(xiàn)象，其非線性特性會(huì)嚴(yán)重影響控制系統(tǒng)的性能，甚至可能導(dǎo)致系統(tǒng)不穩(wěn)定.因此，許多學(xué)者對(duì)具有未知死區(qū)非線性輸入的系統(tǒng)作了大量研究，并取得了一定的成果［1-13］.文獻(xiàn)［1-2］針對(duì)一類(lèi)具有死區(qū)環(huán)節(jié)的非線性系統(tǒng)提出構(gòu)造死區(qū)反函數(shù)來(lái)補(bǔ)償死區(qū)環(huán)節(jié)對(duì)系統(tǒng)帶來(lái)的影響，但是該方法中不光滑的反函數(shù)可能會(huì)導(dǎo)致系統(tǒng)發(fā)生抖振現(xiàn)象.Zhou J.等通過(guò)設(shè)計(jì)光滑的死區(qū)反函數(shù)避免了抖振問(wèn)題［3-4］.文獻(xiàn)［5-6］分別針對(duì)運(yùn)動(dòng)控制系統(tǒng)和直流電機(jī)系統(tǒng)提出了模糊設(shè)計(jì)方法，即根據(jù)專家經(jīng)驗(yàn)設(shè)計(jì)基于模糊邏輯系統(tǒng)的死區(qū)補(bǔ)償器，利用模糊方法構(gòu)造控制器，然而該方案會(huì)過(guò)度地依賴于專家經(jīng)驗(yàn)，當(dāng)找不到合適的描述死區(qū)非線性特性的模糊規(guī)則時(shí)，不能利用這種方法處理死區(qū)問(wèn)題.在文獻(xiàn)［7-9，11-13］中，死區(qū)被分解為一個(gè)線性項(xiàng)和一個(gè)有界的擾動(dòng)類(lèi)似項(xiàng)，然后利用魯棒控制技術(shù)設(shè)計(jì)控制器，取得了理想的控制效果.上述研究均是針對(duì)仿射非線性系統(tǒng)，而大多數(shù)實(shí)際系統(tǒng)如飛控系統(tǒng)、化學(xué)反應(yīng)控制系統(tǒng)等都是非仿射系統(tǒng)，近年來(lái)非仿射非線性系統(tǒng)的研究取得了很多成果［14-17］，遺憾的是針對(duì)非仿射非線性系統(tǒng)的研究，幾乎沒(méi)有人考慮含有死區(qū)輸入的情況.

本文針對(duì)一類(lèi)具有未知死區(qū)輸入環(huán)節(jié)的SISO非仿射非線性系統(tǒng)，給出了一種間接自適應(yīng)模糊控制方法.當(dāng)系統(tǒng)狀態(tài)可測(cè)時(shí)，采用模糊邏輯系統(tǒng)逼近系統(tǒng)中的非線性函數(shù)，構(gòu)造了間接自適應(yīng)模糊控制器.當(dāng)系統(tǒng)狀態(tài)不可測(cè)時(shí)，設(shè)計(jì)觀測(cè)器估計(jì)跟蹤誤差，基于估計(jì)得到的狀態(tài)設(shè)計(jì)間接自適應(yīng)模糊輸出反饋控制器.最后利用Lyapunov穩(wěn)定性定理證明了跟蹤誤差收斂到零的某一鄰域，同時(shí)保證閉環(huán)系統(tǒng)所有信號(hào)有界.

1 問(wèn)題描述

考慮如下一類(lèi)SISO非仿射系統(tǒng)

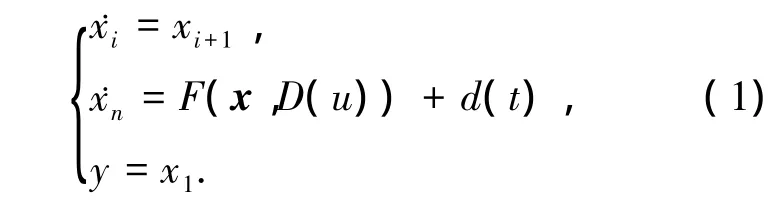
其中:u∈R為系統(tǒng)輸入量，y∈R為系統(tǒng)輸出量，x=［x1，…，xn］T∈Rn為系統(tǒng)的狀態(tài)向量，d(t)為外界干擾且存在常數(shù) d 滿足 |d(t)|≤ d，F(xiàn)(x，D(u))為光滑的未知函數(shù)，D(u)為參數(shù)未知的死區(qū)輸入．

控制目的:設(shè)計(jì)控制器使得系統(tǒng)輸出y跟蹤指定期望軌跡yd，同時(shí)閉環(huán)系統(tǒng)所有信號(hào)均有界．

假設(shè)1 對(duì)于任意x∈Ωx?Rn，存在大于零的常數(shù)g使得函數(shù)，滿足條件g＜g(x)≤成立，其中Ωx為系統(tǒng)的可控域．

假設(shè)2 yd(t)及其對(duì)時(shí)間導(dǎo)數(shù)y(i)d(t)為有界的光滑函數(shù)，i=1，2，…，n．

假設(shè)3 對(duì)于任意x∈Ωx?Rn存在常數(shù)gr使得|·g(x)|≤gr成立．

輸入為u輸出為D(u)的死區(qū)模型描為

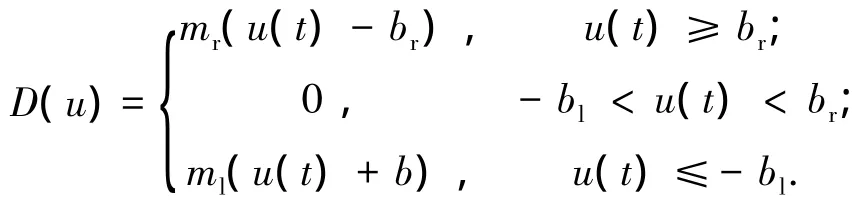
死區(qū)模型滿足條件:1)死區(qū)輸出D(u)不可測(cè);2)死區(qū)參數(shù)未知，滿足0≤br≤br，0≤bl≤bl，0＜ml≤ml，0＜mr≤mr．

將未知死區(qū)轉(zhuǎn)化為

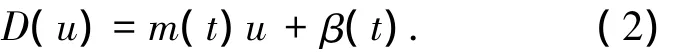
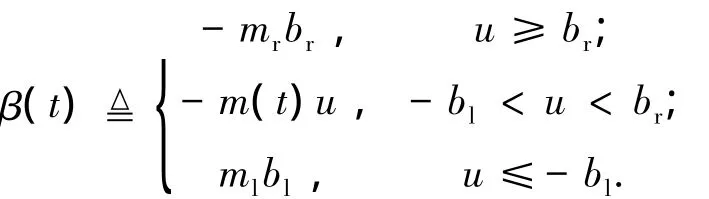
2 自適應(yīng)模糊控制器設(shè)計(jì)

首先利用中值定理將非仿射非線性形式轉(zhuǎn)化為仿射非線性形式，有

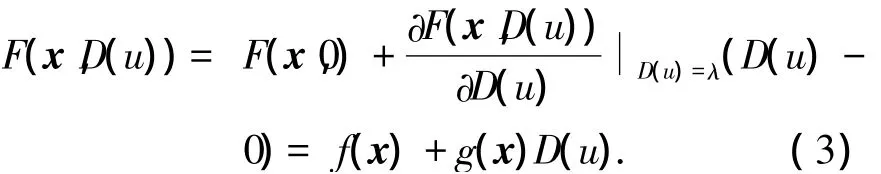
其中:f(x)=F(x，0)，λ ∈［0，D(u)］，

結(jié)合式(2)，系統(tǒng)(1)可轉(zhuǎn)換為

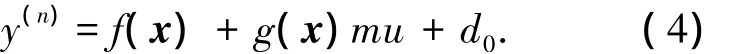
其中:d0=g(x)β(t)+d(t)，則存在大于零的常數(shù)0使得 |d0|≤0．

針對(duì)經(jīng)轉(zhuǎn)化得到的仿射非線性系統(tǒng)，分系統(tǒng)狀態(tài)可測(cè)與不可測(cè)兩種情況進(jìn)行分析.

2.1 系統(tǒng)狀態(tài)可測(cè)

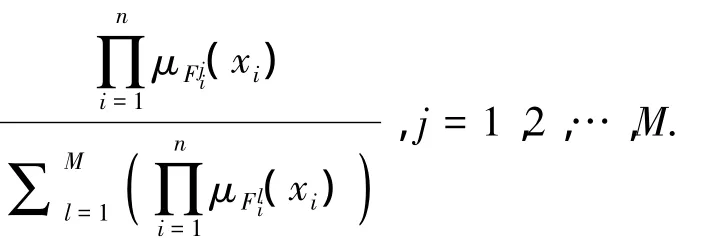
根據(jù)模糊邏輯系統(tǒng)的萬(wàn)能逼近特性［18］，存在最優(yōu)逼近參數(shù)分別滿足

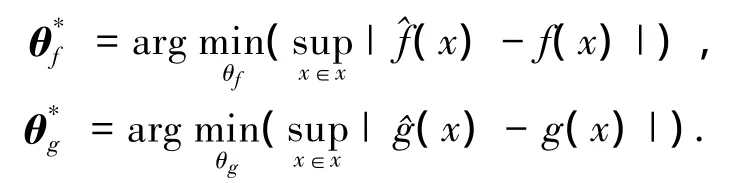
估計(jì)誤差為

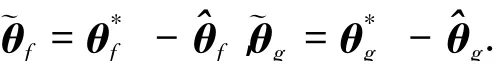
定義最優(yōu)逼近誤差為

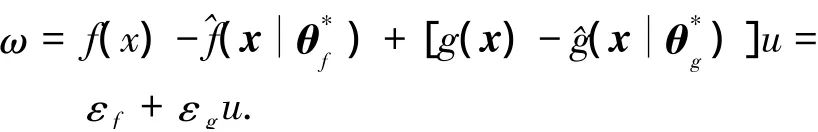
定義跟蹤誤差e=yd-y，則誤差向量e=［e，，…，e(n-1)］T．

由式(3)有系統(tǒng)跟蹤誤差方程為

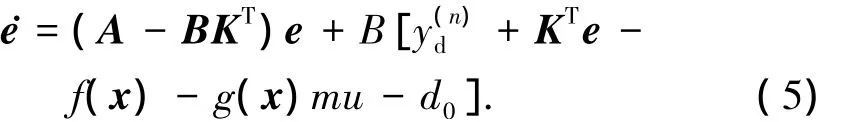
式中:B=［0…01］T，

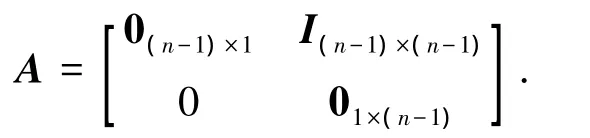
選擇向量 K= ［kn，kn-1，…，k1］T使得 sn+k1sn-1+k2sn-2+kn為Hurwitz多項(xiàng)式．因此A1=A-BKT為穩(wěn)定的矩陣，即給定一個(gè)正定對(duì)稱矩陣P，存在正定矩陣Q滿足Lyapunov方程

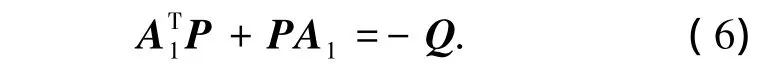
定理1 對(duì)于系統(tǒng)(1)，采用如下控制律與自適應(yīng)律，可以使得系統(tǒng)輸出跟蹤給定期望信號(hào)，同時(shí)保證閉環(huán)系統(tǒng)所有信號(hào)均有界.

控制律為

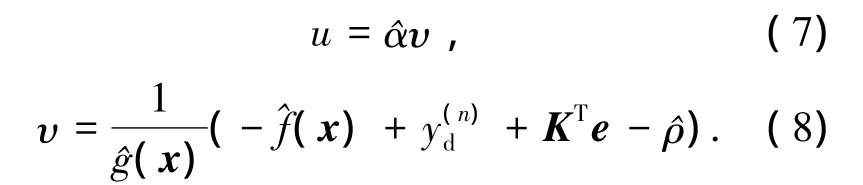
自適應(yīng)律為

其三，巡檢工作不到位。在城市燃?xì)夤艿劳度脒\(yùn)行之后，城市燃?xì)夤艿老嚓P(guān)單位承擔(dān)著管道運(yùn)行維護(hù)的責(zé)任，它們需要組織人員對(duì)管道日常運(yùn)行進(jìn)行巡檢，及時(shí)發(fā)現(xiàn)并排除一些潛在的安全隱患或是突發(fā)問(wèn)題，這樣可以最大程度的避免燃?xì)庑孤妒鹿实陌l(fā)生。然而在實(shí)際工作中，管道運(yùn)行巡檢工作不到位的情況十分常見(jiàn)，這也為燃?xì)庑孤堵裣铝穗[患。

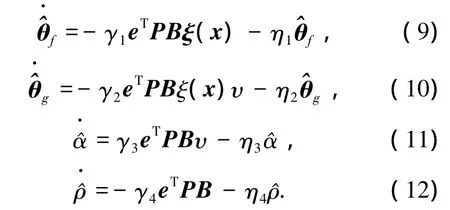
證明 取如下Lyapunov候選函數(shù)

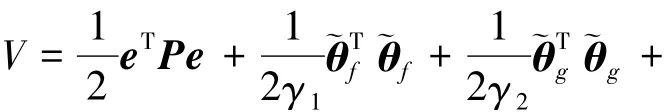
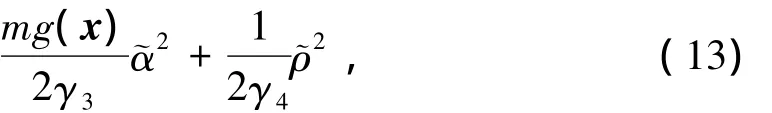
對(duì)V求時(shí)間的導(dǎo)數(shù)并結(jié)合(5)、(6)可得

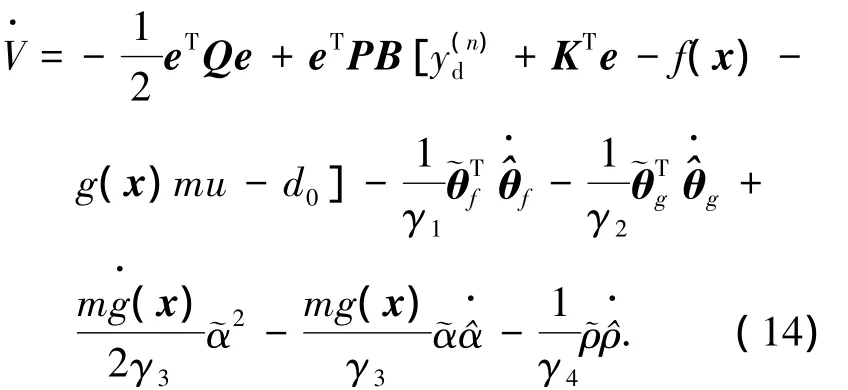
將控制律式(7)、(8)以及自適應(yīng)律式(9)～(12)代入式(14)整理可得

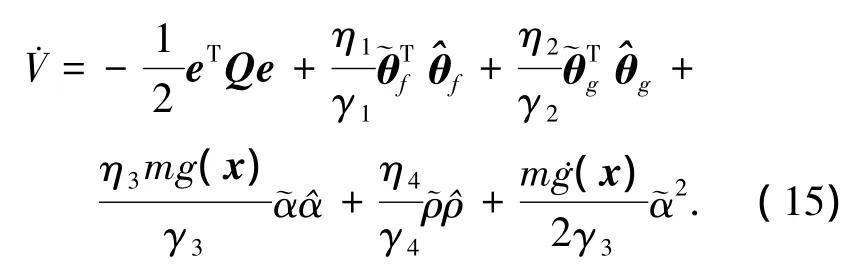
根據(jù)假設(shè)1和假設(shè)3，利用不等式性質(zhì)整理式(15)有

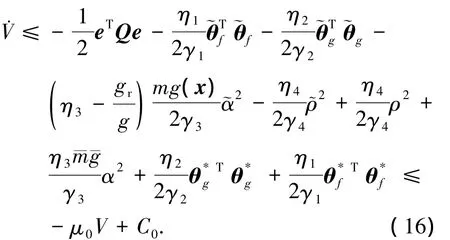
其中:μ0=，選取 η3使得 η3-＞0．

由式(16)可得

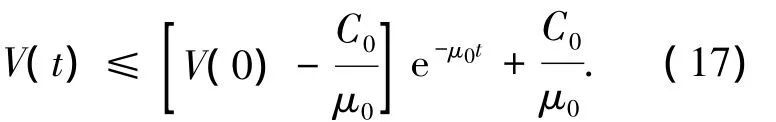
2.2 系統(tǒng)狀態(tài)不可測(cè)

在實(shí)際工程中，通常只有系統(tǒng)輸出可測(cè)，而系統(tǒng)狀態(tài)通常是不可測(cè)量的，即y可測(cè)，=［x2，…，xn］T不可測(cè)．此時(shí)只能利用狀態(tài)的估計(jì)=［1，…，n］T設(shè)計(jì)間接自適應(yīng)模糊控制器．

跟蹤誤差向量為e=［e，，…，e(n-1)］T，定義

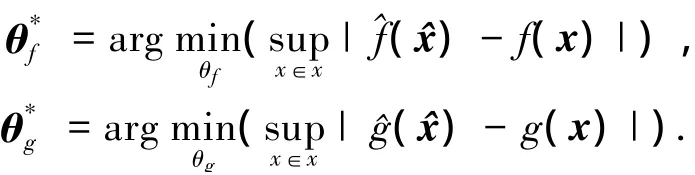
參數(shù)誤差為

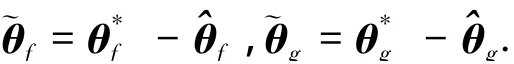
定義f(x)和g(x)的最優(yōu)逼近誤差為

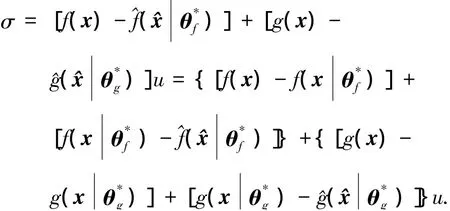
由式(4)可得系統(tǒng)跟蹤誤差方程為

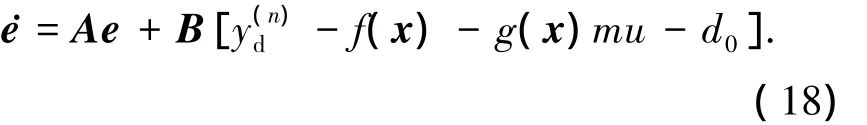
設(shè)計(jì)誤差觀測(cè)器為

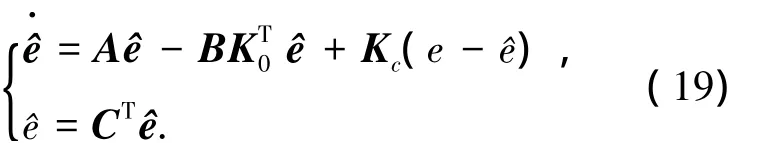
式中:C=［1，0，…，0］T為反饋增益為觀測(cè)器增益，選擇K0、Kc分別使A-、A-KcCT為穩(wěn)定矩陣．

假設(shè)4 正定矩陣P1和P2分別滿足方程

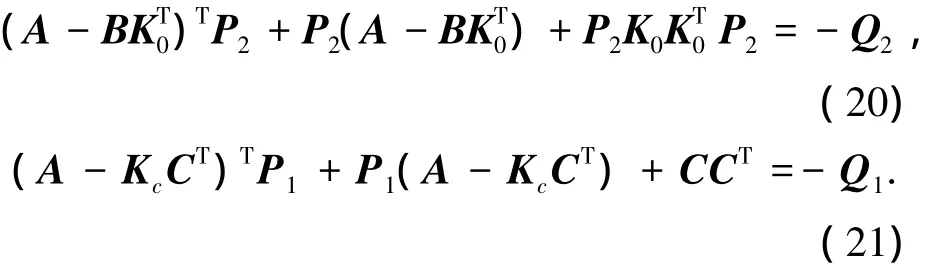
由式(18)、(19)可得

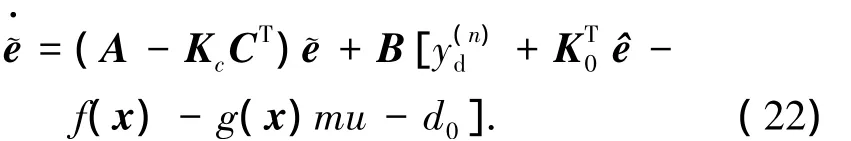
定理2 對(duì)于系統(tǒng)(1)，當(dāng)系統(tǒng)狀態(tài)不可測(cè)時(shí)，采用如下控制律和自適應(yīng)律，可以使得系統(tǒng)輸出跟蹤給定期望信號(hào)，同時(shí)保證閉環(huán)系統(tǒng)所有信號(hào)均有界.

控制律

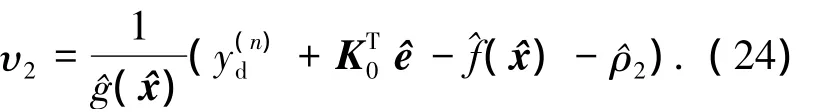
自適應(yīng)律

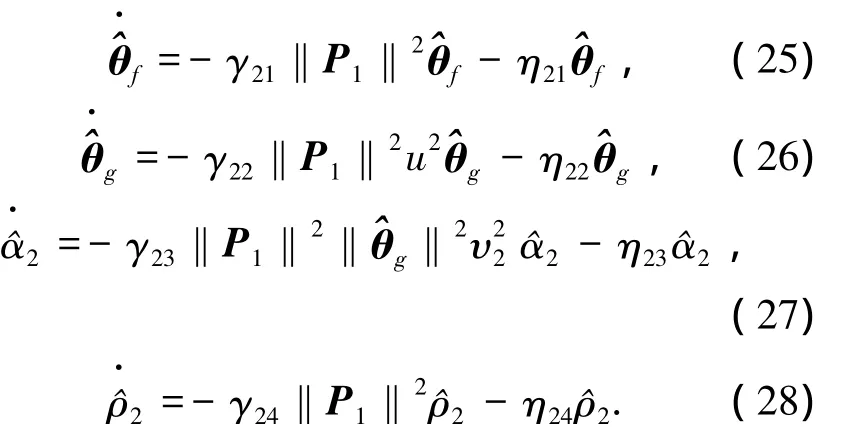
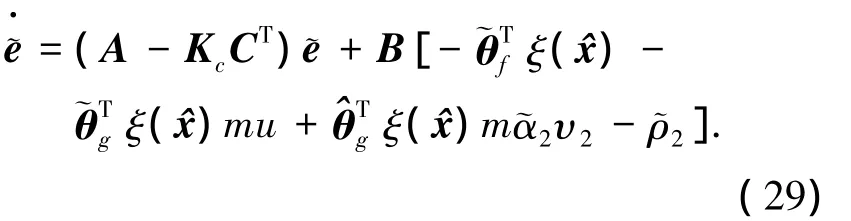
構(gòu)造如下Lyapunov候選函數(shù)

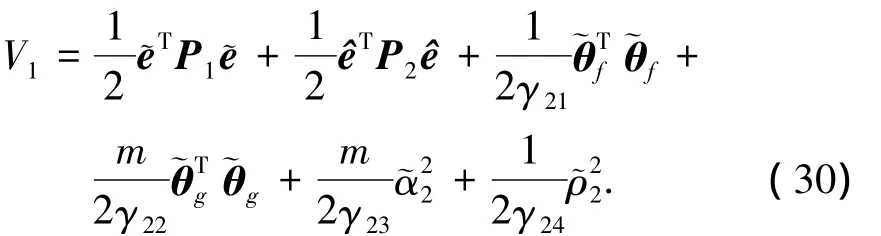
求V1關(guān)于時(shí)間的導(dǎo)數(shù)

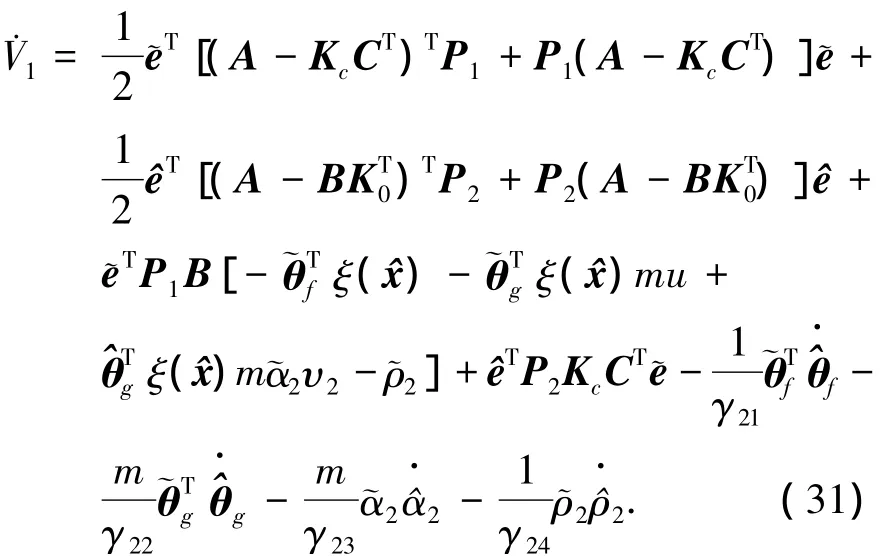
將式(20)、(21)代入式(31)有

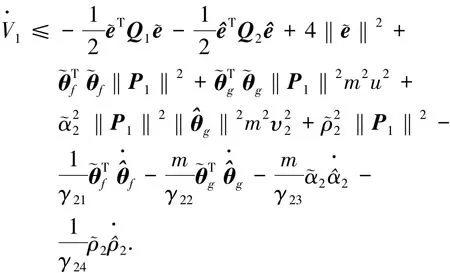
整理可得

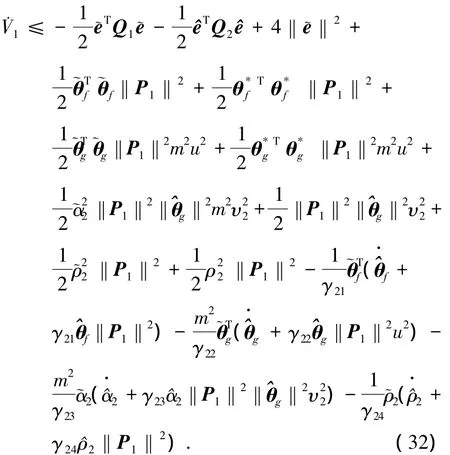
假設(shè)存在常數(shù) M、N、?分別滿足不等式|u|≤M，|υ|≤N，‖θg‖2≤?．將自適應(yīng)律式(25)～(28)代入式(32)整理有

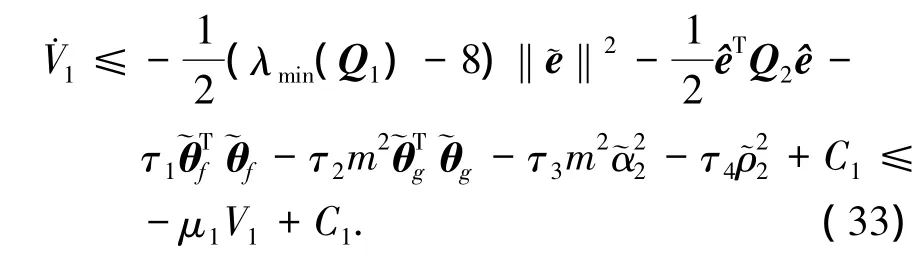
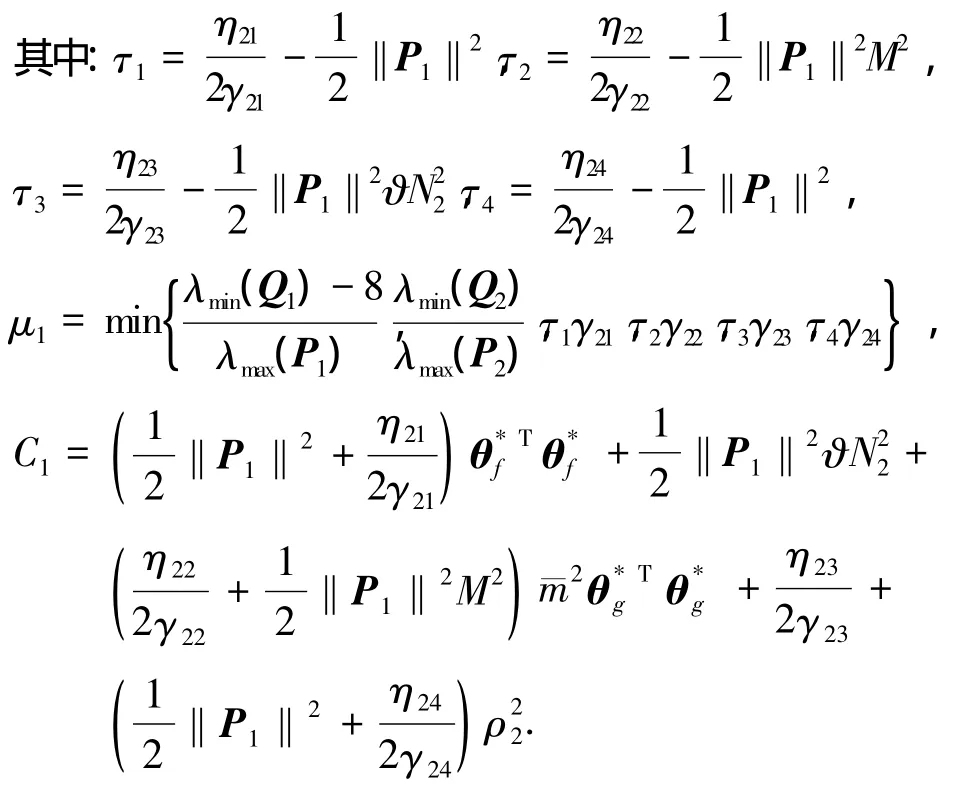
對(duì)式(33)兩端求積分有

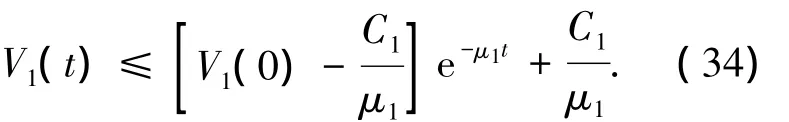
3 仿真結(jié)果

考慮如下非仿射非線性系統(tǒng)

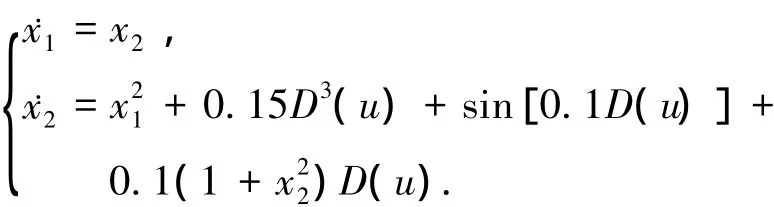
仿真目的是驗(yàn)證所設(shè)計(jì)控制器能使系統(tǒng)的輸出y跟蹤期望軌跡yd=sin(t)．仿真實(shí)驗(yàn)將分系統(tǒng)狀態(tài)可測(cè)與不可測(cè)兩種情況進(jìn)行．其中死區(qū)D(u)定義為

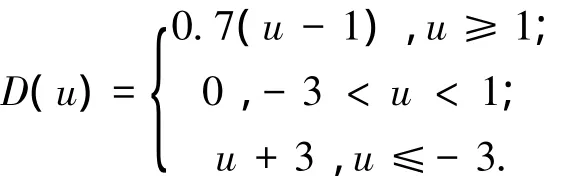
模糊隸屬度函數(shù)選取分別為

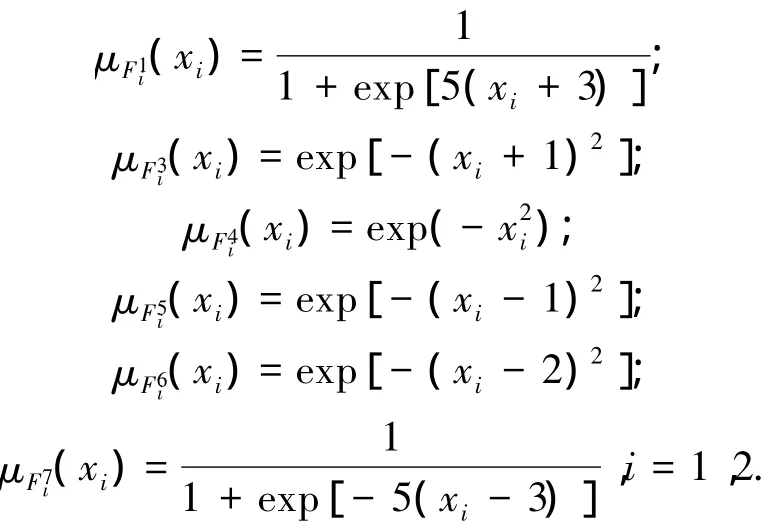
狀態(tài)可測(cè)時(shí)，參數(shù)取值:γ1=0.01、γ2=0.01、γ3=0.01、γ4=0.01、η1=0.08、η2=0.08、η3=0.08、η4=0.08、K=［2510］T、P=．仿真過(guò)程中初值設(shè)定(0)=0.1(0)= ［0.1…0.1］1×49、x1(0)=1、=［0.1…0.1］1×49、x2(0)=0．仿真時(shí)間為30 s，仿真結(jié)果如圖1～3所示．

狀態(tài)不可測(cè)時(shí)，參數(shù)取值:γ21=0.01、γ22=0.01、γ23=0.01、γ24=0.01、η21=0.001、η22=0.001、η23=0.001、η24=0.001、K0=［104］T、Kc=［45］T、P1=．仿真初值設(shè)定:［0.1…0.1］1×49(0)=［10］T．仿真時(shí)間取為30 s，結(jié)果如圖4～6所示.

由圖1和圖4可以觀察到系統(tǒng)輸出跟蹤期望信號(hào)的軌跡，結(jié)合跟蹤誤差圖2和圖5，可以得出結(jié)論，利用本文所設(shè)計(jì)的控制器，可以使得系統(tǒng)完成跟蹤任務(wù)，即跟蹤誤差收斂于零的某一鄰域.圖3和圖6則分別給出了兩種情況下系統(tǒng)控制輸入的軌跡曲線.經(jīng)上述分析，本文給出的控制器能夠使得系統(tǒng)輸出跟蹤給定軌跡，并同時(shí)保證了跟蹤誤差收斂以及控制輸入有界.

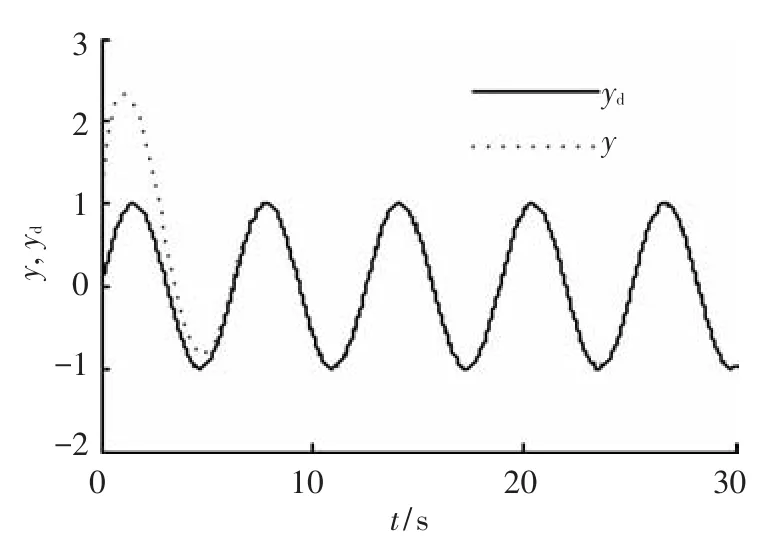
圖1 狀態(tài)可測(cè)時(shí)期望輸出與實(shí)際跟蹤曲線

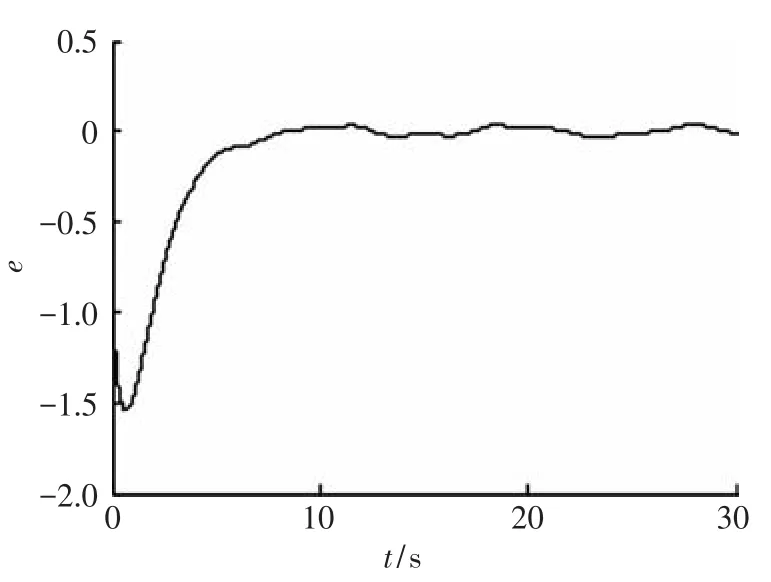
圖2 狀態(tài)可測(cè)時(shí)跟蹤誤差曲線

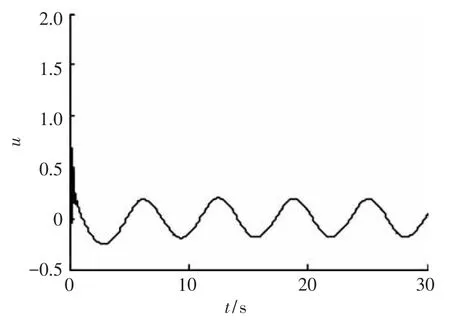
圖3 狀態(tài)可測(cè)時(shí)系統(tǒng)控制輸入曲線

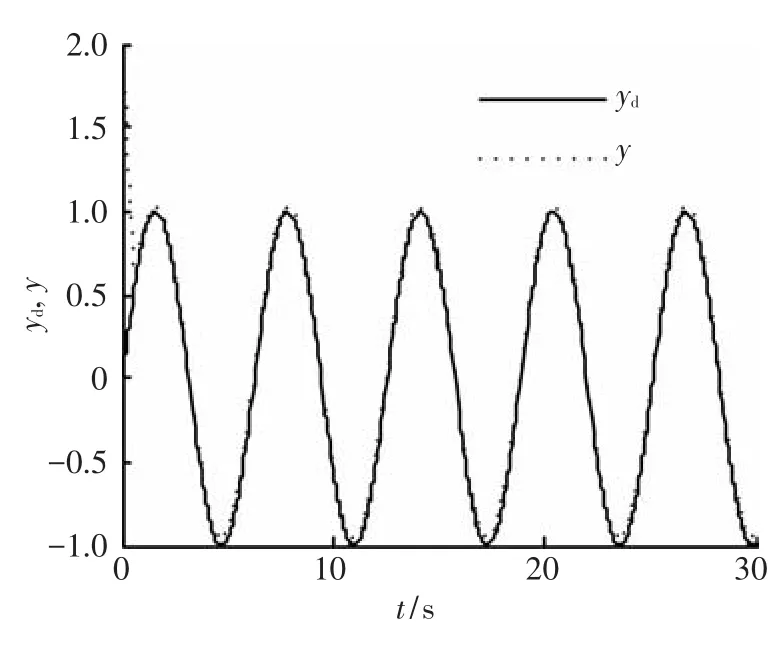
圖4 狀態(tài)不可測(cè)時(shí)期望輸出與實(shí)際跟蹤曲線

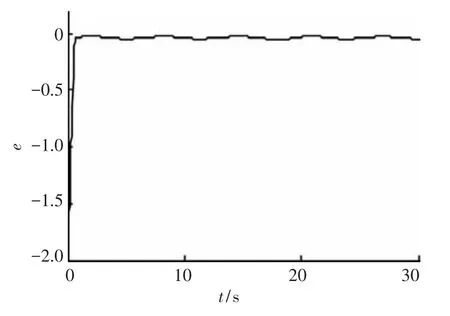
圖5 狀態(tài)不可測(cè)時(shí)跟蹤誤差曲線

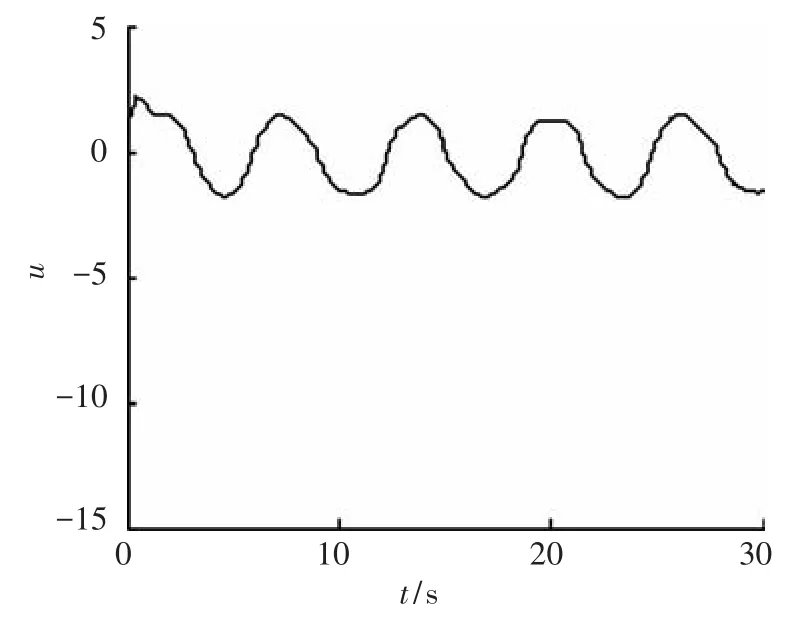
圖6 狀態(tài)不可測(cè)時(shí)系統(tǒng)控制輸入曲線

5 結(jié) 論

1)研究了一類(lèi)含有未知死區(qū)輸入環(huán)節(jié)的SISO非仿射非線性系統(tǒng)控制器設(shè)計(jì)問(wèn)題，給出了在系統(tǒng)狀態(tài)可測(cè)與不可測(cè)兩種情況下的控制器設(shè)計(jì)方案.

2)通過(guò)Lyapunov定理證明了具有未知死區(qū)的SISO非仿射非線性閉環(huán)系統(tǒng)的穩(wěn)定性，跟蹤誤差收斂，同時(shí)保證了所有系統(tǒng)均有界.

［1］CHO H，BAI E.Convergence results for an adaptive dead zone inverse ［J］.Int J Adapt Control Signal Processing，1998，12(5):451-466.

［2］TAWARE A，TAO Gang，TEOLIS C.Design and analysis of a hybrid control scheme for sandwich nonsmooth nonlinear systems［J］.IEEE Trans Autom Control，2002，47(1):145-150.

［3］ZHOU Jing，WEN Changyun，ZHANG Ying.Adaptive output control of nonlinear systems with uncertain deadzone nonlinearity ［J］.IEEE Trans Autom Control，2006，51(3):504-511.

［4］ZHOU Jing，SHEN X Z.Robust adaptive control of nonlinear uncertain plants with unknown dead-zone［J］.IET Control Theory Appl，2007，1(1):25-32.

［5］LEWIS F L，TIM W K，WANG L Z，et al.Dead-zone compensation in motion control systems using adaptive fuzzy logic control［J］.IEEE Trans Contr Syst Technol，1999，7(6):731-742.

［6］JANG J O.A dead-zone compensator of a DC motor system using fuzzy logic control［J］.IEEE Trans Man，Systems and Cybernetics:Applications and Reviews，2001，31(1):42-48.

［7］WANG Xingsong，SU Chunyi，HONG H.Robust adaptive control of a class of linear systems with unknown dead-zone ［J］.Automatica，2004，40(3):407-413.

［8］張?zhí)炱剑釗P(yáng)，梅建東.帶有未知死區(qū)模型的魯棒自適應(yīng)模糊控制［J］.控制與決策，2006，21(4):367-370.

［9］IBRIR S，XIE Wenfang，SU Chunyi.Adaptive tracking of nonlinear systems with non-symmetric dead-zone input［J］.Automatica，2007，43(3):522-530.

［10］沈啟坤，張?zhí)炱?具有未知非線性死區(qū)的自適應(yīng)模糊控制［J］.控制與決策，2007，22(6):689-692.

［11］HUA Changchun，WANG Qingguo，GUAN Xinping.Adaptive tracking controller design of nonlinear systems with time-delays and unknown dead-zone input［J］.IEEE Trans Autom Control，2008，53(7):1753-1759.

［12］ADLOO H，NOROOZI N，KARIMAGHA P.Observer based model reference adaptive control for unknown time-delay chaotic systems with input nonlinearity ［J］.Nonlinear Dynamic，2012，67:1337-1356.

［13］TONG Shaocheng，LI Yongming.Adaptive fuzzy output feedback control of MIMO nonlinear systems with unknown dead-zone inputs［J］.IEEE Trans Fuzzy Syst，2013，21(1):134-146.

［14］LABIOD S，GUERRA T M.Adaptive fuzzy control of a class of SISO nonaffine nonlinear systems［J］.Fuzzy Sets Syst，2007，158(10):1126-1137.

［15］WEN Jie，JIANG Changsheng.Adaptive fuzzy controller for a class of strict-feedback nonaffine nonlinear systems［J］.Journal of Systems Engineering and Electronics，2011，22(6):967-974.

［16］MAO Zhizhong，XIAO Xiaoshi.Decentralized adaptive tracking control of nonaffine nonlinear large-scale systems with time-delays ［J］.Inf Sci，2011，181(23):5291-5303.

［17］BOULKROUNE A，MSAAD M，F(xiàn)ARZA M.Adaptive fuzzy tracking control for a class of MIMO nonaffine uncertain systems ［J］.Neurocomputing，2012，93:48-55.

［18］WANG Lixin.A course in fuzzy systems and control［M］.Englewood Cliffs，NJ:Prentice Hall，1997.