GPS高程平面擬合法的應用

常紅斌，蘇恒

(1.新疆電力設計院，新疆烏魯木齊 830000;2.武漢市測繪研究院，湖北武漢 430022)

1 引言

目前，水準測量和三角高程測量是高程傳遞的兩種最常見的手段，GPS水準高程擬合是眾多測量專業研究的一種新的高程測量方法，也在一些工程中得到了很好的應用。常規的高程測量方法勞動強度大，投入的人力物力多，操作復雜，效率低下，發生錯誤時不易查找，尤其是長距離的高程傳遞更是非常辛苦，而GPS水準高程恰恰可以解決以上難題，簡單又經濟。

2 GPS高程擬合概述

眾所周知，GPS高程是相對于WGS84橢球的高度，稱為大地高H84，而我們常用的高程系統是正常高Hr，是相對于似大地水準面的高度，兩者之間的差距通常稱為高程異常ζ，三者的關系為:

似大地水準面是一個與地球形狀比較接近的不規則的曲面，所以如何求得高精度的大地高和高程異常是我們大家一直探討的問題［1］。靜態GPS高程測量通過延長觀測時間、增加觀測時段和避開多路徑效應等手段可以得到高精度的大地高。而高程異常的推算相對比較復雜，常用的方法大致可分為:①多項式曲線擬合法;②三次樣條曲線擬合法;③Akima曲線擬合法;④多項式曲面擬合法;⑤多面函數曲面擬合法;⑥移動曲面擬合法等。前3種方法適用于GPS控制網布設成測線時使用，后3種方法適用于GPS控制網布設成網狀時使用［2］。目前工程測量應用中最常用的是多項式曲面擬合法，此方法又分為平面擬合法和二次曲面擬合法，基本原理是:在一定區域內，高程異常呈平緩變化，利用測區內一定數量已知點的大地高和正常高求解出各點的高程異常值，將這些高程異常值近似看作一定范圍內各點坐標的曲面函數，用這一函數計算其余GPS點的高程異常和正常高。這一模型函數可以表達為:

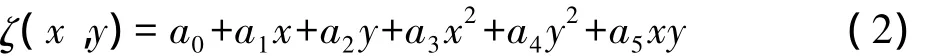
當測區內已知點數少于3個時，只能求出a0一個系數，當已知點數大于3個且小于6個時，可以求解出平面擬合中的a0、a1、a2三個系數，當已知點數大于6個時，可以求解出曲面擬合中的所有系數［3，4］。平面擬合法一般適用于高程異常變化平緩的平地或低丘地區，二次曲面擬合法適用于高程異常呈拋物單曲面地區，或似大地水準面呈兩個以上凹凸面時使用，但已知點數量要達到6個以上且均勻分布于整個測區［5］，所以當控制點稀少的地方且地形趨勢變化不大的地方用GPS高程平面擬合的方法較適用。為此我們通過工程實例對這一方法進行了驗證和總結。

3 目前工程應用

現在，大多數工程都以曲面擬合法為主。一般作業步驟如圖1所示:

在選取GPS高程擬合點時應選取均勻分布于測區周圍的點和具有地形特征的點，做平面擬合時至少需要3點以上，做曲面擬合時應至少選取6點以上。內符合精度是將參與計算的高程點的異常值與計算后得到的異常值進行比較，求出殘差，按相應公式求解出內符合精度。外符合精度是將沒參與擬合的GPS水準高程和擬合過的高程值進行比較，求解出擬合殘差，按相應公式求解出外符合精度［6，8］。

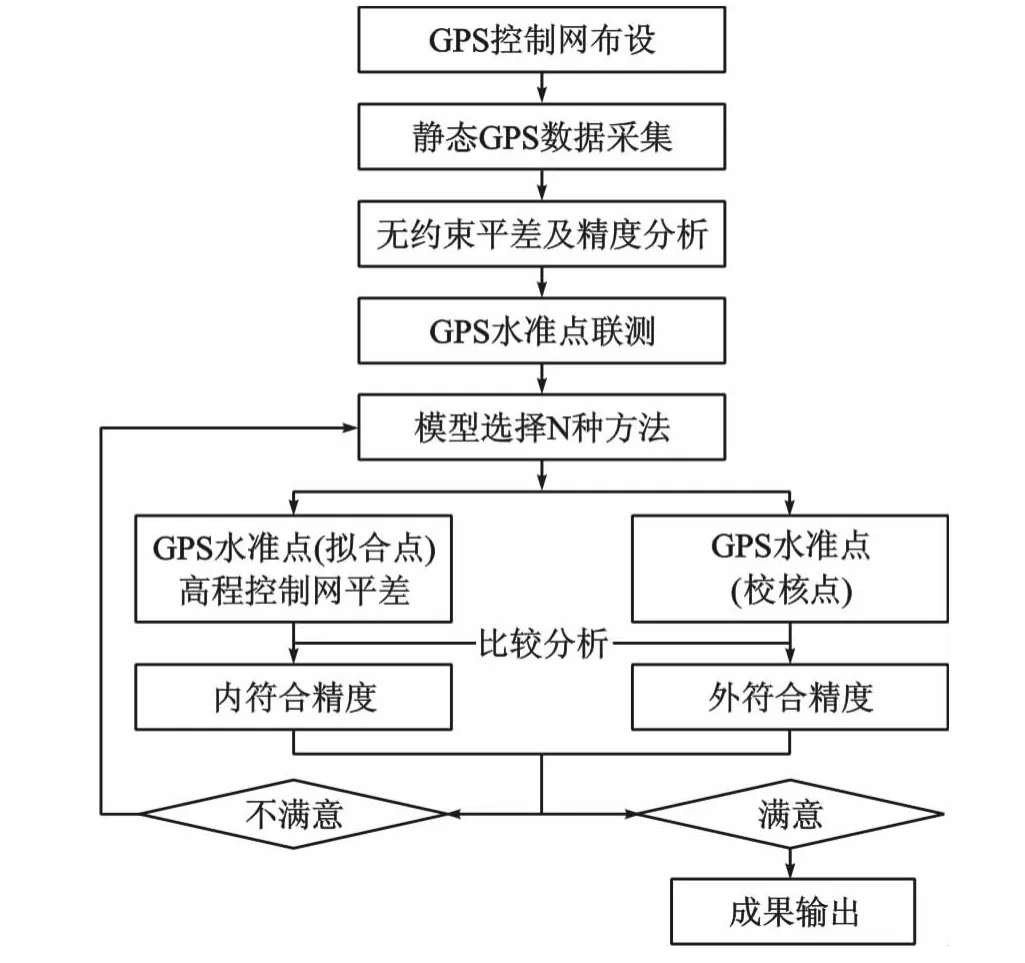
圖1 GPS水準作業流程圖

4 工程實例

4.1 測區概況

工程實例測區位于某市附近，由于當地控制點遭到嚴重破壞，且是冬天，天氣寒冷，積雪較厚，為水準聯測工作帶來極大困難，但為驗證此方法的可行性，為以后工作提供經驗，作者單位還是做了四等水準的測量工作。經實地踏勘后只找到離測區相對最近的4個可靠且保存完好的控制點，其中GL與TYC為一等水準高程，YSG與GTL為三等水準高程，高程基準為1985國家高程基準，4點之間地形基本都為平地，地面起伏比較平緩，測區位于4點范圍內。內業經基線解算和無約束平差后得到4個水準點的高程異常值，數據如表1所示:

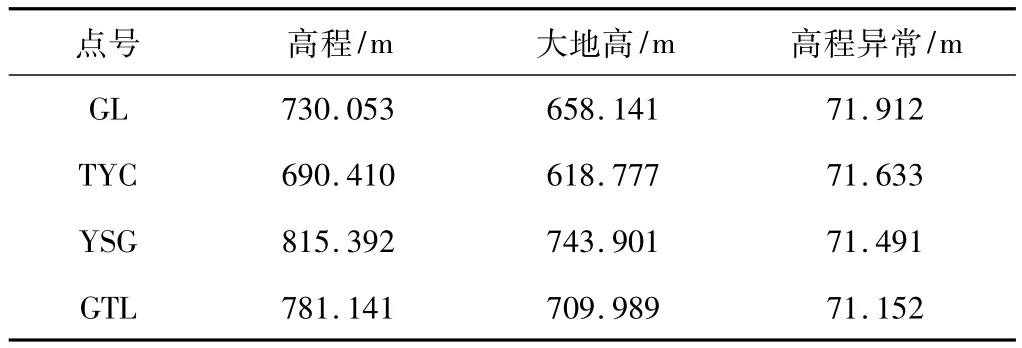
控制點高程異常值 表1

從表1可以看出該地區的高程異常變化比較平緩，4個已知水準點間距離較遠，最近約為 16 km，最遠約為 27 km，測區內布設E01－E05，本工程要求做測區內的控制測量工作，高程基準要求1985國家高程基準，控制網分布圖如圖2所示:

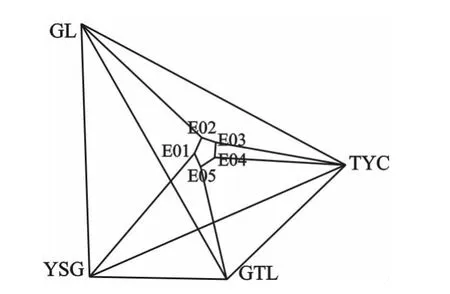
圖2 控制網分布圖

4.2 水準聯測

本工程水準測量路線為一附合路線，順序為GL－E01－E02－E03－E04－E05－TYC，外業施測按四等水準要求進行施測，內業采用Power Adjust 2005軟件進行平差，經平差后得各點的高程值，具體過程略，數據如表2所示。

測區內高程控制點成果 表2

4.3 GPS網觀測

由于收集到的控制點距離較遠，所以本次外業施測均采用雙時段觀測，每個時段觀測時間都大于60 min，使用5臺雙頻GPS接收機進行同步觀測，儀器高量測至毫米，外業觀測完后對數據采用中海達軟件進行數據處理，模型采用平面高程模型。

4.4 不同網形結構數據處理分析［7］

由于本次所有觀測點精度相同，所以檢測點就任意選取測區中的E01和E04作為檢測點。

(1)選取任意一個控制點構網進行高程擬合，檢查其余已知點及E01與E04，高程中誤差均在 2 m左右，擬合高程數據不可用。

(2)選取任意兩個控制點構網進行高程擬合，檢查其余已知點及E01與E04，高程中誤差均在 1 m左右，擬合高程數據不可用。

(3)選取GL、TYC、GTL三個控制點構網進行高程擬合，檢查另一已知點及E01與E04，最大高程中誤差為 0.004 m，測區位于擬合范圍內，擬合高程可以滿足四等水準測量精度要求。

(4)選取GL、TYC、YSG三個控制點構網進行高程擬合，檢查另一已知點及E01與E04，最大高程中誤差為 0.003 m，測區位于擬合范圍內，擬合高程可以滿足四等水準測量精度要求。

(5)選取GL、YSG、GTL三個控制點構網進行高程擬合，檢查另一已知點及E01與E04，最大高程中誤差為 0.007 m，測區位于擬合范圍外，但距離擬合范圍較近，擬合高程數據精度可能不滿足四等水準測量精度要求，但可以滿足等外水準測量精度要求。

(6)選取GTL、TYC、YSG三個控制點構網進行高程擬合，檢查另一已知點及E01與E04，最大高程誤差為 0.005 m，測區位于擬合范圍外，但距離擬合范圍較遠，擬合高程數據精度不能滿足四等水準測量精度要求，也不滿足等外水準測量精度要求。

(7)選取4個控制點構網進行高程擬合，檢查E01與E04，最大高程中誤差為 0.003 m，測區位于擬合范圍內，擬合高程可以滿足四等水準測量精度要求。

不同網形擬合的誤差統計如表3所示:

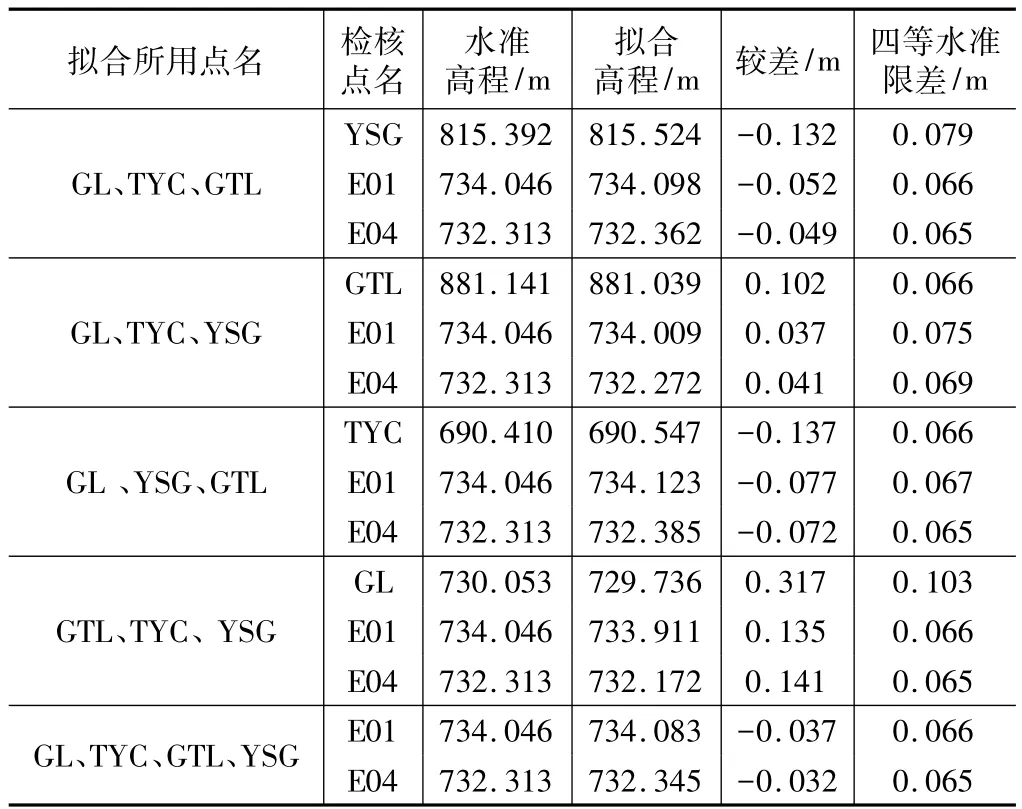
誤差統計表 表3

(8)選取4個已知點和測區內任意一點或兩點進行擬合，其余點擬合高程與水準高程都非常接近，誤差均在毫米級，這是由于測區比較小而且比較平，所以高程擬合的精度較高。

5 結論

(1)在控制點稀少且高程異常變化平緩的區域或聯測水準有困難的情況下，可以用GPS高程平面擬合的方法代替四等水準，但高程擬合至少需要3個點，且測區應分布于3個點組成的擬合范圍內。

(2)對高程擬合外的高程精度將隨著距離擬合面的增大而降低，不能滿足四等水準測量精度要求，但距離原擬合面較近時可以滿足普通水準的精度要求。

(3)對超出高程擬合外的高程中誤差不可信［9］。

(4)結合以往案例和相關資料得知，GPS高程擬合的精度主要取決于:GPS大地高的精度、GPS水準聯測精度、GPS水準點分布情況及數量、高程擬合模型的選擇等四大因素。

在以上因素都能保障的情況下，GPS高程擬合精度可以達到四等水準測量的精度要求。

［1］徐紹銓，張華海，楊志強.GPS測量原理及應用［M］.武漢:武漢大學出版社，2004.

［2］王明華，李浩.GPS高程擬合的模型優選［OL/DB］.中國科技論文在線，2005.

［3］趙云，曹先密.平坦地區GPS高程異常擬合方法研究［J］.測繪工程，2010，19(3):24～25.

［4］郟紅偉.GPS水準測量應用探討［J］.測繪通報，2005(8):29～52.

［5］南親江，卜建陽.GPS高程曲面擬合算法的精度分析［J］.現代測繪，2008，31(4):17～19.

［6］蔡慶立.基于二次曲面擬合的區域似大地水準面確定［J］.礦山測量，2010(4):24～26.

［7］伍青云.GPS高程擬合的方式及可靠性分析［J］.現代測繪，2006(4):29～31.

［8］沈云中，高達凱，張興福.GPS水準點優化選擇法［J］.工程勘察，2004(6):49～51.

［9］鄧連利.在GPS測量中起算點對高程精度的影響分析［J］.西部探礦工程，2012(5):145～146.