最大準則優化技術在貼體網格中的應用

賈艷艷，邢學軍，史基安，孫國強

1中國科學院油氣資源研究重點實驗室，蘭州 730000

2中國科學院大學，北京 100049

3中國石油冀東油田公司，唐山 063004

1 引言

目前我國油氣勘探已轉移到西部地區，西部地區劇烈起伏的地形給地震勘探提出了嚴峻的挑戰，經典反射地震勘探技術在復雜地表地區不再適用，地震波數值模擬中的網格法由于具有對地形和介質靈活劃分的特點成為解決此類問題最有效的方法.網格法以結構網格或非結構網格對模擬對象進行離散，一般而言，基于非結構網格的模擬方法要比基于結構網格的模擬方法需要更多計算量（董良國，2005；王雪秋和孫建國，2008；朱多林和白超英，2011；孫小東等，2012）.貼體網格是為適應復雜幾何邊界而出現的一種結構網格，該網格已在計算流體力學中廣泛應用，目前也在地球物理模擬中推廣應用（孫章慶等，2009；孫建國和蔣麗麗，2009；蘭海強等，2011；Lan and Zhong，2011；劉一峰和蘭海強，2012）.貼體網格生成方法主要有代數法、插值法、保角變換法和偏微分方程法（陶文銓，2001；蔣麗麗和孫建國，2008）.這些方法生成貼體網格時，必須首先給定離散的邊界條件.目前對面向地質條件的貼體網格生成技術研究不足，尤其在生成網格時對邊界離散優化方法研究不足.邊界的離散優化問題可描述為給定節點量的曲線逼近和曲面網格優化問題，本文研究內容集中在給定節點量的曲線逼近和曲面網格優化方法，以解決在地質條件下的貼體網格生成中的邊界離散問題.

在數值模擬和可視化技術中，曲線和曲面分別以折線段和四邊形去逼近.雖然學者對曲線逼近和曲面網格優化做了很多研究，大部分研究都是自由曲線曲面的造型技術（吳福鳴和潘日晶，2011；甘屹等，2002）.雖然理論相對成熟，但并不適合給定幾何形狀和節點量的曲線逼近和曲面網格優化.文中，我們提出最大長度準則、最大面積準則、最小距離修正法和限定網格步長的優化算法，以實現曲線逼近和曲面網格優化，為貼體網格生成提供高質量的離散邊界.

曲線作為平面和曲面的邊界，在二維貼體網格生成時必須先根據節點量完成曲線離散，離散結果要盡可能的逼近曲線形狀.最常逼近曲線的方法有樣條法、圓弧法和直線段法（王振祿等，2007；孫彤和童小華，2010；鄭永前等，2011）.雖然貼體網格在物理域上是以曲線作為邊界，但在網格生成時并不會關心相鄰節點間曲線形狀.因此，利用樣條曲線段和圓弧段逼近曲線的方法在貼體網格生成中很少應用，目前生成網格時主要用直線段來逼近曲線.直線段逼近曲線的方法主要有：等間距法、等步長法、等誤差法.等間距法無法自動實現復雜曲線形狀的逼近，等誤差法無法限定節點數量，故只有等步長法適合給定節點量的曲線逼近.等步長法具有實施簡單、效率高的特征，但在實施過程中沒有考慮曲線形狀特征.本文依據最大長度準則實現定節點量的直線段逼近曲線，根據該準則離散優化的折線段能很好地反應原曲線的幾何形狀，該準則對機械加工、數值模擬、曲線顯示都具有重要意義.

曲面作為三維幾何體的邊界，通常以三角形和四邊形進行曲面離散.三維貼體網格邊界以四邊形結構網格形式離散.通常離散方法有插值算法、NURBS曲面逼近、偏微分方程法等（朱心雄，2001；楊旭東等，2002；吁日新和朱自強，2003；梅中義和范玉青，2003）.這些方法均不含對網格的優化過程，目前曲面網格主要的優化方法有：Laplacian光順方法、等參數修勻法（田紅等，2009）.Laplacian光順方法將內部節點移至與其相鄰共線結點坐標的平均值處，等參數修勻是將網格內部節點的坐標修改為相鄰共面結點坐標的平均值.這兩種優化方法都沒有考慮優化對曲面網格形狀特征的影響，文中，我們提出一種新的四邊形曲面結構網格的優化算法，最大面積準則優化法.在不改變網格拓撲結構和節點數量的條件下使得網格能最多的描述幾何體的邊界形狀.最大面積準則優化的網格不適用于數值計算，文中提出了限定網格步長的優化算法，可優化數值計算的網格.

最大準則的優化問題求解費時.為解決此問題我們提出改進型單粒子優化算法.單粒子優化算法的思想來源于粒子群優化算法，粒子群優化算法（Particle Swarm Optimization algorithm，PSO），也可以稱為微粒群算法，最早是由美國的心理學研究者Kennedy博士和從事計算智能研究的Eberhart于1995年提出的一種基于群智能的隨機搜索算法（Kennedy and Eberhart，1995）.該算法最初是受到鳥類群體活動規律性的啟發，進而利用群體智能建立的一個簡化模型.由于該算法概念簡明、實現方便、收斂速度快、參數設置少，是一種高效的搜索算法，近年來受到學術界的廣泛重視.但在優化復雜高維多模函數時，PSO算法很容易陷入局部最優，并出現早熟收斂現象.為了改善算法性能，Eberhart和Kennedy于1995提出了全局粒子群算法和局部粒子群算法（Eberhart and Kennedy，1995）.Shi和Eberhart于1998年對PSO算法的速度項引入了慣性權重，并提出在進化過程中動態調整慣性權重以平衡收斂的全局性和收斂速度（Shi and Eberhart，1998）.Angeline于1998年將進化計算中的標準選擇機制引入到粒子群優化算法中，提出了帶選擇機制的粒子群優化算法（Angeline，1998）.Clerc和Kenndy于2002年提出了帶收縮因子的粒子群優化算法（Clerc and Kennedy，2002）.Mendes和Kennedy于2004年提出了一種信息充分共享的粒子群優化算法（Mendes etal，2004；Kennedy and Mendes，2006）.紀震于2010年提出了智能單粒子優化算法（Intelligent Single Particle Optimizer，ISPO），確保算法在優化復雜的具有大量局部最優化點的高維多模函數方面的優勢（紀震等，2010）.本文在ISPO算法的基礎上，提出了改進的單粒子優化算法，該算法能高效求解給定節點量的曲線逼近和曲面優化問題.

2 限定節點量的曲線逼近和曲面網格優化

2.1 限定節點量的曲線逼近

直線逼近空間曲線時，應做到節點在曲線曲率變化大的位置密集，在曲率變化小的位置疏散，而等步長法在逼近空間曲線時忽略了該關鍵點.本文利用最大長度準則解決此問題.最大長度準則是在給定曲線形狀和節點量的條件下，直線段長度和最大的離散結果能更好地描述曲線.

最大長度準則定義為：設Q＝｛xi｜i＝1，2，…，N｝為曲線上N個節點集合，該曲線的形狀由f（x）給出，L為集合Q組成的折線段長度，若Lmax為任意集合Q組成折線段的長度集合中的最大值，則組成Lmax的集合Q所描述的曲線最逼真.下面通過實例展示最大長度準則和等步長法的對比結果.

我們采用y＝30sin（3πx／100），0≤x≤100的曲線來說明根據最大長度準則逼近曲線的性能.圖1至圖4是最大長度準則法和等步長法的對比結果.從圖1和圖2可以看出，以最大長度準則逼近曲線時，在描述曲線形狀，逼近誤差方面均優于等步長法.圖3說明以最大長度準則逼近曲線時用少量節點數就能接近原曲線的長度，而等間距法需要用大量節點才能接近原曲線長度，故最大長度準則逼近曲線的誤差小于等步長法.圖4說明兩種方法的節點平均斜率跳躍值相近，最大長度準則結果略好于

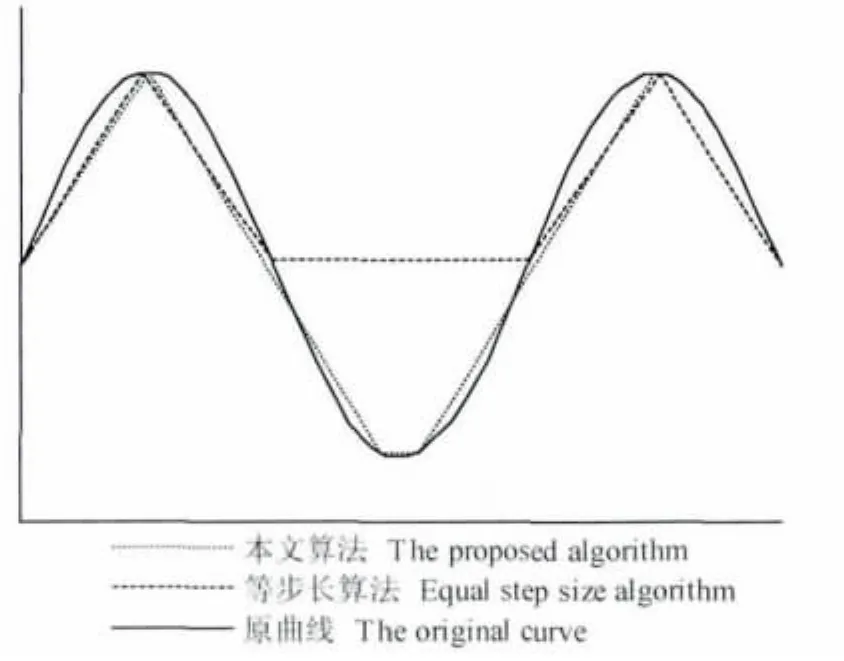
圖1 節點量為6的曲線逼近效果對比Fig.1 Comparison of six-node curve approximation by two methods

圖2 節點量為21的曲線逼近效果對比Fig.2 Comparison of twenty-one node curve approximation by two methods

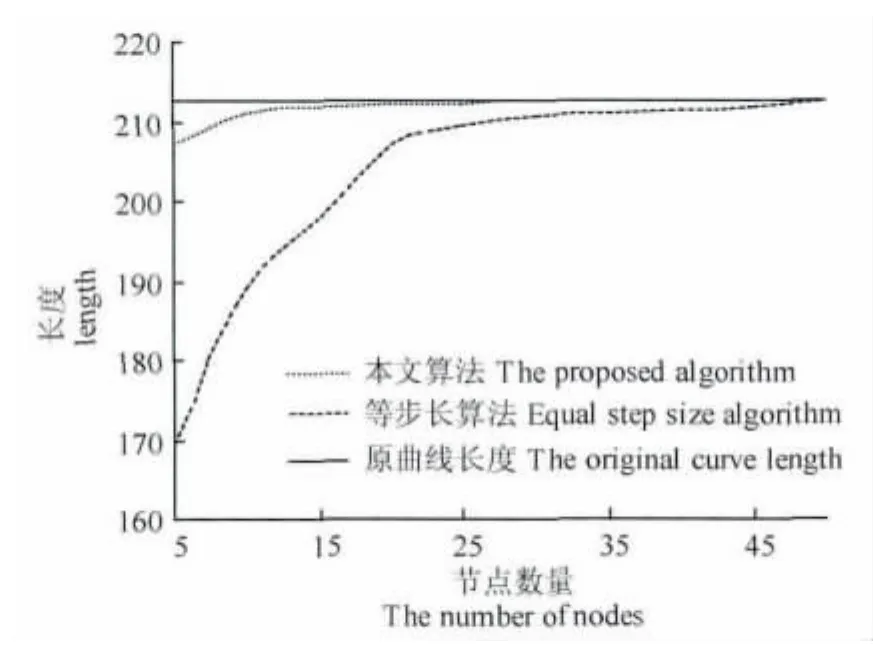
圖3 兩種逼近算法生成直線的長度與原曲線長度的對比Fig.3 Comparison of curve lengths generated by two approximation algorithms and the original curve length

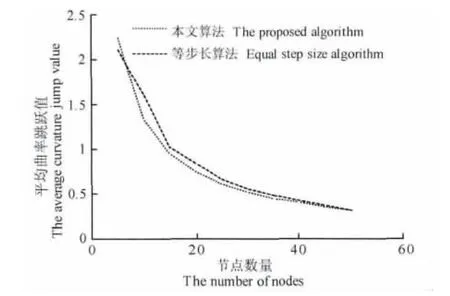
圖4 兩種逼近算法生成節點的平均斜率跳躍值的對比Fig.4 Comparison of mean curvature jumping values generated by two approximation algorithms

等步長法，平均斜率跳躍值為

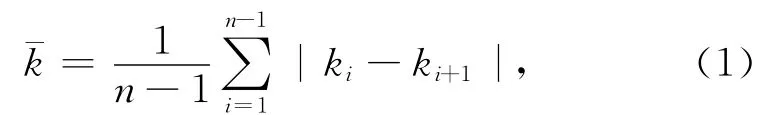
2.2 限定節點量的曲面網格優化

曲面網格優化方法中，Laplacian光順法和等參數修勻法主要用于數值模擬計算網格的優化，這兩種方法均沒有考慮優化對曲面網格形狀的影響.本文提出的最大面積優化準則可實現限定節點量曲面網格優化，使網格描述的曲面形狀更加逼真.

最大面積優化準則定義為：設Q＝｛xi，j｜i＝1，2，…，N；j＝1，2，…，M｝為曲面上N×M個節點集合，該曲面的形狀由f（x）給出，S為集合Q組成四邊形網格的面積，若Smax為任意集合Q組成四邊形網格的面積集合中的最大值，則組成Smax的集合Q所描述的曲面最逼真.

圖5 等參數修勻法生成原始曲面網格Fig.5 Original surface grid generated by optimization-based smoothing

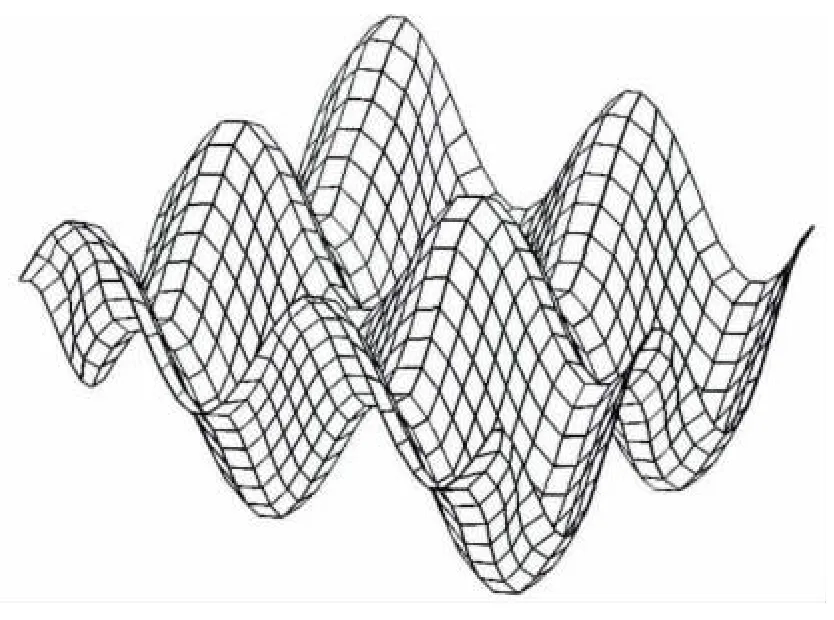
圖6 Laplacian光順方法優化曲面網格的效果圖Fig.6 Surface grid optimized by Laplacian smoothing

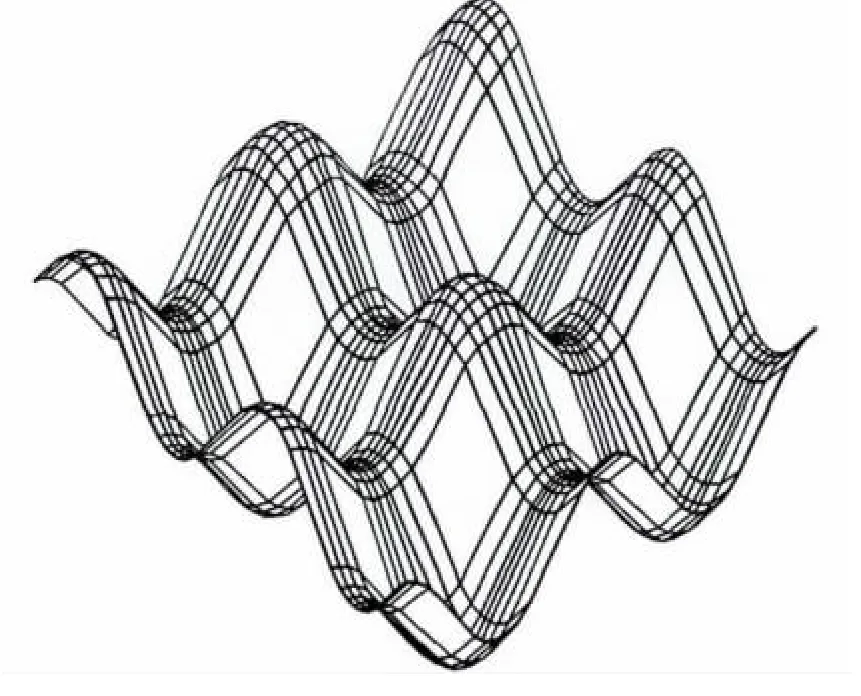
圖7 最大面積準則優化曲面網格的效果圖Fig.7 Surface grid optimized by maximum area criteria

本文采用z＝30sin（πx／50）+30cos（πy／50），0≤x≤200，0≤y≤200的曲面來說明最大面積準則優化曲面網格時的性能.根據圖5至圖7可以看出，用Laplacian光順法優化等參數修勻法生成的網格后網格步長趨于一致，而用最大面積準則優化的網格在法曲率半徑變化大位置（谷和峰）網格密集.從圖8中可以看出，最大面積準則優化的網格面積最大，Laplacian光順法優化的網格面積小于等參數修勻法生成的網格面積.因此，最大面積準則優化的網格在用于曲面顯示時效果好于Laplacian光順法和等參數修勻法，能更好地描述曲面.

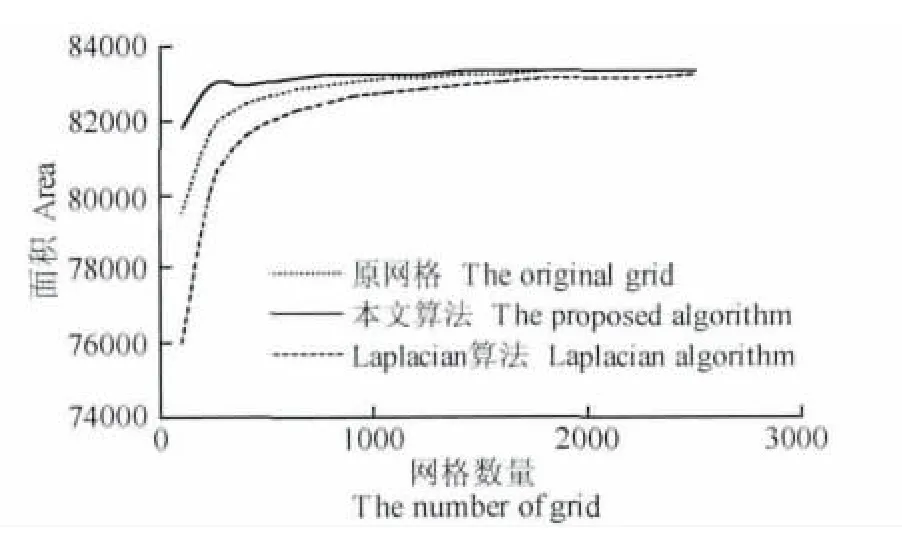
圖8 三種網格的面積對比圖Fig.8 Area comparison of three kinds of grids

3 改進的單粒子優化算法在曲線逼近和曲面網格優化中的應用

根據最大準則將曲線逼近和曲面網格優化問題抽象為數學優化問題，即為給定曲線（曲面）上節點數量，尋找一組滿足最大準則的節點.為求解此優化問題，文中提出了改進的單粒子優化算法.ISPO算法的計算耗時主要花費在適應值計算上，求解一次適應值的耗時會隨著粒子維數增加而增加，使得總求解耗時隨粒子維數急劇增加（紀震等，2010）.本文提出的改進單粒子優化算法吸收了ISPO算法的學習策略和多樣性部分，同時改進了適應值的計算.在改進的單粒子優化算法中以子粒子與其鄰近子粒子的關系建立局部適應值函數，通過求解局部適應值來完成粒子更新，從而達到提高求解速度的目的.ISPO算法根據實際問題的目標函數直接建立適應值函數，而改進的單粒子優化算法需要根據實際問題對目標函數進行分析以建立局部適應值函數.

3.1 改進的單粒子優化算法

在改進的單粒子優化算法中，整個N維矢量被分為N個子維矢量，定義為N個子粒子，即把整個位置矢量分解成N個子粒子位置矢量，每一個子粒子位置矢量與它對應的速度矢量被分別表示成~zj和~vj，j＝1，…，N；每個子粒子用局部適應值判斷其影響域內局部解的優劣性，以循環迭代更新子粒子位置的方法求得整體粒子的最優解.其算法原理描述如下：

（1）子粒子.將N維粒子分解為N個子粒子，每個子粒子有自己的位置矢量和速度矢量.如用N-1段線段去逼近一段曲線，曲線產生包含端點在內N個節點.這N個節點組成一個粒子，每一個節點為一個子粒子，即為N個子粒子.

（2）更新過程.改進單粒子優化算法的更新過程是每個子粒子位置矢量按照先后順序從~z1到~zN進行循環求解，用每個子粒子在當前局部條件下的最優位置更新相應子粒子位置矢量，迭代執行D次或者達到全局最優時結束迭代.更新子粒子時速度和位置調整公式為

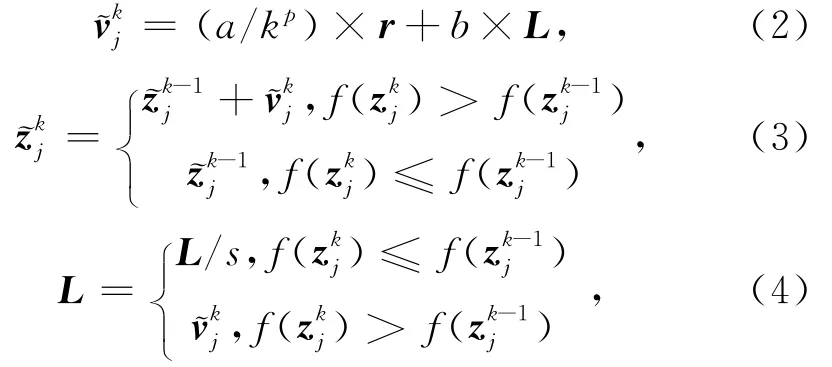
算法流程如下：

（2）設置第一個計算子粒子的位置，即j＝0；

（5）若i小于3，則轉到（3）計算；否則判斷j與N的大小；

（6）若j不大于N，則j＝j+1，L＝0，并轉到（3）循環計算；否則判斷k與D的大小；

（7）若k大于D，則結束計算；否則k＝k+1，并轉到（2）循環計算.

在子粒子矢量更新過程中，子粒子速度矢量決定著位置矢量，每個子粒子速度矢量包括兩個部分：學習部分b×L和多樣性部分（a／kp）×r.多樣性部分（a／kp）會隨著迭代次數的增加而下降，這樣可以使得優化的收斂速度加快.學習部分b×L是根據子粒子上一次的速度更新情況智能地調整子粒子速度矢量，使子粒子速度具有更大的多樣性，避免陷入局部最優.

3.2 改進的單粒子優化算法在曲線逼近中的應用及性能分析

在曲線逼近時，最大長度準則優化問題的目標函數描述為

其中N為節點數，Li，i+1為節點i和i+1之間的直線距離.根據ISPO算法的適應值函數定義，式（5）為ISPO算法的適應值函數.從式（5）中不難發現，當節點i的位置發生變化時，只對距離Li-1，i和Li，i+1有直接影響.故曲線逼近優化問題的目標函數也可以近似描述為

max（Li-1，i+Li，i+1）（i＝12，…，N-1）， （6）文中以式（6）作為改進的單粒子優化算法求解曲線逼近優化問題的局部適應值函數，每一個節點為改進的單粒子優化算法的子粒子.在文中采用y＝30sin（πx／100），0≤x≤1000函數曲線分析兩種優化算法的性能，分析結果如圖9所示，在節點為200時，以改進的單粒子優化算法的計算效率已是ISPO算法的30倍左右.

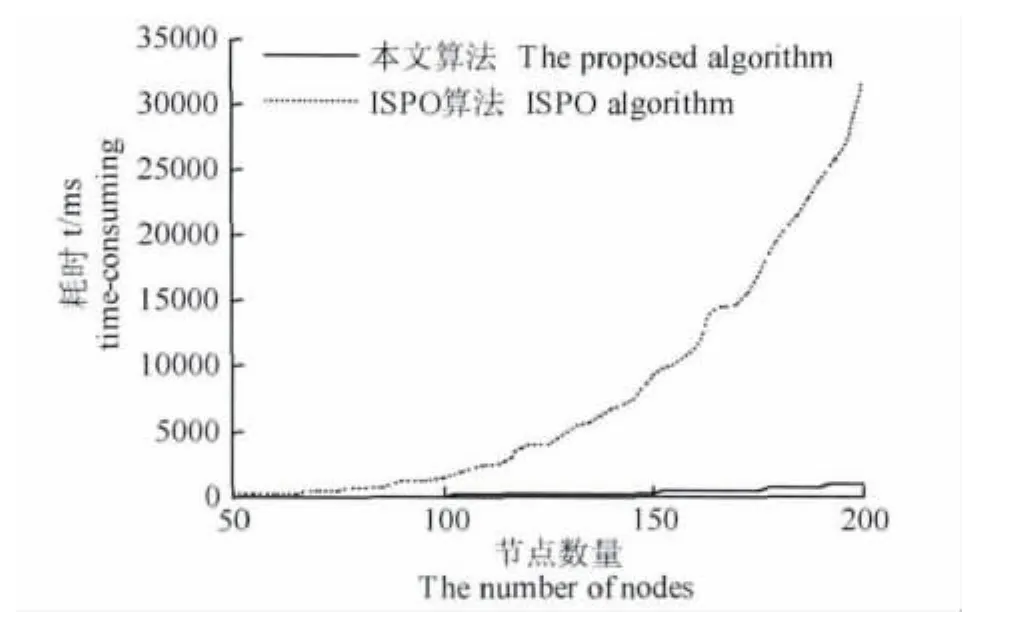
圖9 兩種算法優化耗時的對比圖Fig.9 Comparison of time-consuming of two optimizers

3.3 改進的單粒子優化算法在曲面網格中的應用

本文借鑒網格能量法的思想，間接實現最大面積準則對曲面網格的優化，即采用最大長度準則和最小距離修正法優化曲面網格線.最小距離修正法為節點與相鄰節點的距離之和最小，以保證網格中不會產生圖10所示的畸形網格，使網格保持光順.

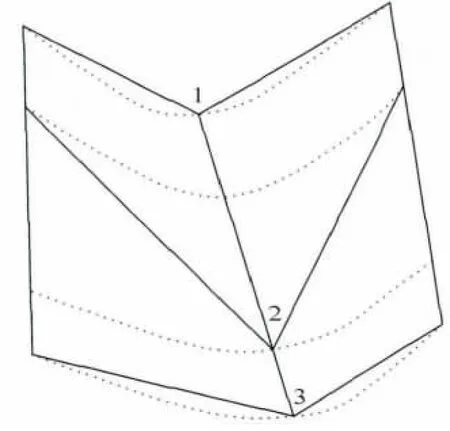
圖10 畸形網格Fig.10 Distorted grid

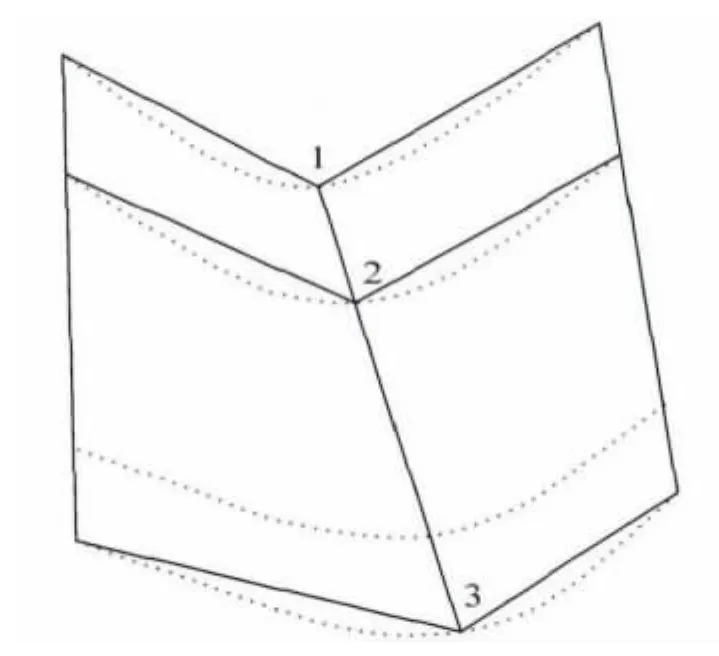
圖11 修改后的網格Fig.11 Modified grid

從圖10和圖11可以看出，經最小距離修正法處理后的網格正交性改善.類比改進的單粒子優化算法在曲線逼近中的應用，可實現改進的單粒子優化算法對曲面網格優化問題的求解.

最大面積準則優化曲面網格算法流程如下：

（1）根據曲面網格的特性將網格曲線分為兩族，同一族的曲線互不相交，分別定義為X方向的曲線和Y方向的曲線；

（2）根據最大長度準則優化Y方向的曲線；

（3）根據最大長度準則優化X方向的曲線；

（4）根據最小距離修正法修正曲面網格；

（5）重復執行（2）至（4）步，直到滿足收斂要求.

4 最大準則優化算法及限定網格步長的優化算法在地質體貼體網格中應用

最大準則優化曲面網格能提高網格質量，可更好地描述曲線曲面形狀.最大準則優化的網格可更好地描述地質體的谷、峰、地勢平坦和坡度變化較小的區域.圖13所示網格是根據圖12所示等高線圖生成的三維貼體網格，從圖12和13可以看出：A類標記的位置為地勢平坦或者坡度變化較小區域，網格間距較大；B類標記的位置為凹陷的谷底區域，網格較密；C類標記的位置為凸起的峰頂區域，網格較密.因此，網格在坡度變化較大區域密集而在坡度變化較小區域稀疏，能更好地描述出地質體特征.

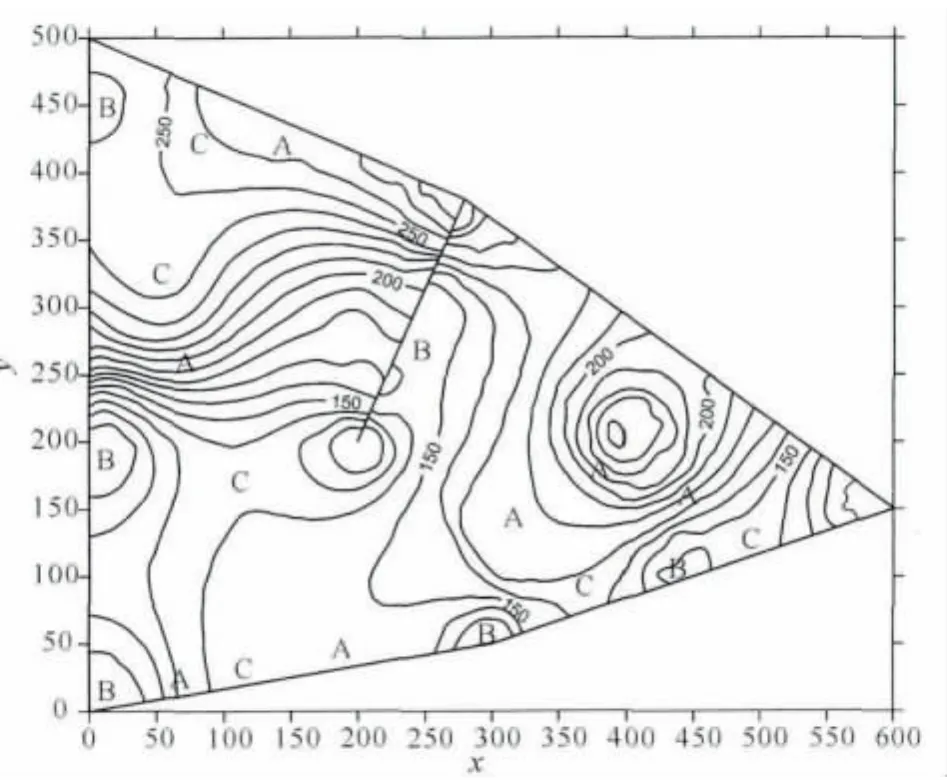
圖12 地質體的等高線圖Fig.12 Contour lines of a geology body

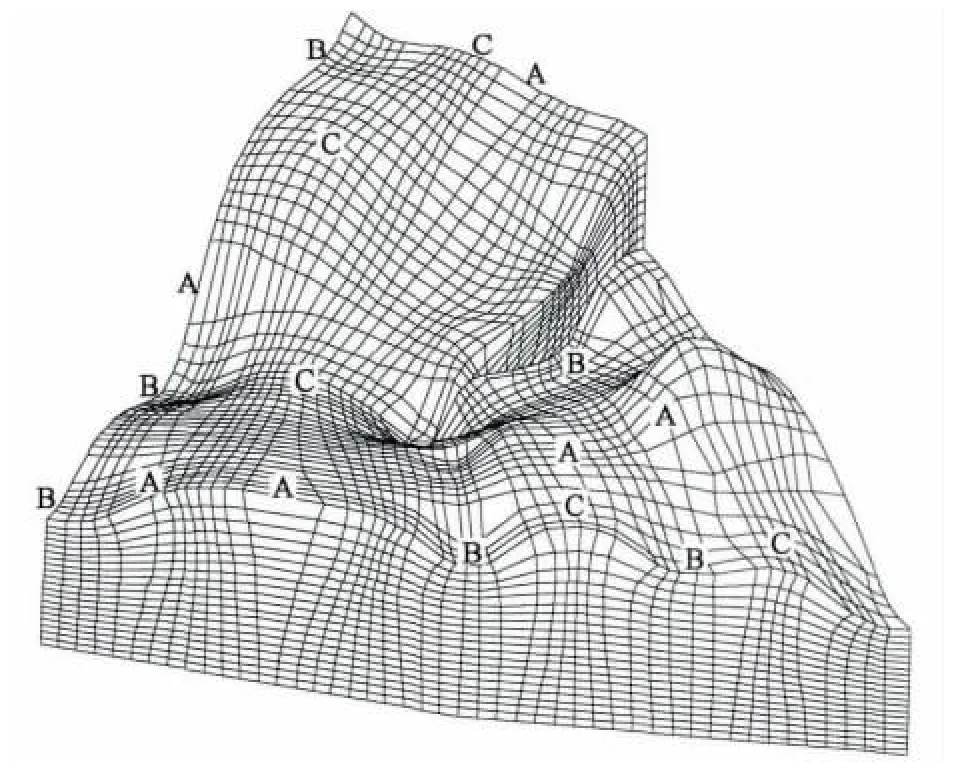
圖13 最大準則優化的三維貼體網格邊界Fig.13 Boundaries of a three dimensional body-fitted grid optimized by maximum criteria

數值計算中要求網格具有合理的步長范圍和良好的正交性.為將地質體網格（圖13）用于數值計算，本文提出了限定網格步長的優化算法.該算法引入最大步長系數amax和最小步長系數amin，使生成網格步長均勻.圖14為限定網格步長的優化算法優化圖1 3網格的結果圖（其中amax為1.2，amin為0.8），從圖看出優化后的網格步長得到控制，消除了細條狀和面積過大的網格；圖15為文本算法與Laplacian光順算法優化圖13網格后網格線夾角大小分布圖（網格夾角數為14400），從圖可知，兩種算法優化網格后網格線夾角分布范圍一致，而本文算法在85°～95°之間分布高，在其它范圍內的分布低，說明本文算法優化的網格具有更好地正交性.根據限定網格步長優化算法優化逼近曲線的最大長度準則折線段的算法流程如下：

（1）初始化網格曲線長度最大步長系數amax和最小步長系數amin；

（2）初始化節點標號i＝1，并設置判斷修正結束因子k＝0；

圖14 限定網格步長優化算法優化的三維貼體網格邊界Fig.14 Boundaries of a three-dimensional body-fitted grid optimized by the limited grid step length algorithm

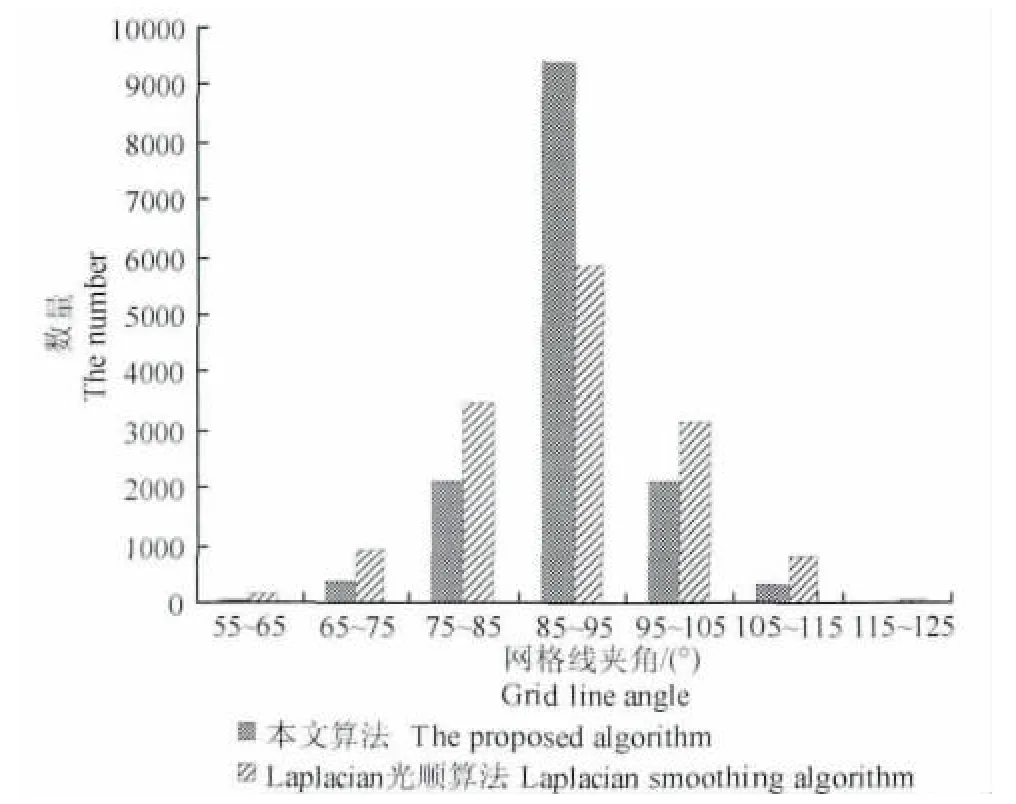
圖15 網格線正交性分布圖Fig.15 Orthogonality distribution columns of grid lines

（3）計算網格曲線的長度，求得步長的平均值Lave；

（6）若i大于1且小于N-1，則跳轉到（8）步，否則繼續往下執行；

（7）若i等于N，則優化曲線段的節點下標為：j1＝N-2，j2＝N-1，j3＝N，否則j1＝0，j2＝1，j3＝2，并跳轉到（12）步；

（14）若i小于節點數N，則i＝i+1，并轉到（3），否則向下執行；

（15）若k等于1，則設置i＝1和k＝0，并轉到（3），否則結束計算.

5 結論

通過對生成貼體網格中邊界離散技術的研究，提出了最大準則、限定網格步長的優化算法和改進的單粒子優化算法，使邊界離散技術得以提高，可生成高質量的貼體網格.

本文提出的最大長度準則逼近曲線的性能高于等步長法，能在確定節點量的條件下最大限度地描述出原曲線形狀，為二維貼體網格和空間曲面網格生成打好基礎.根據最大面積準則優化的曲面網格能很好地保持原曲面形狀，且網格光順.為求解最大準則的優化問題，文中提出了改進的單粒子優化算法，該算法求解曲線逼近和曲面網格優化問題的效率遠高于ISPO算法.為解決最大準則優化曲面網格步長無法控制的問題，本文引入限制網格步長的優化算法，通過該算法優化曲面網格，生成的新網格在保證網格步長不超出要求范圍內的同時具有更好的正交性.通過各種對比分析說明，本文提出的最大長度準則、最大面積準則、最小距離修正法、限定網格步長的優化算法和改進的單粒子優化算法性能都高于目前的優化算法，為生成高質量的貼體網格及其在地球物理模擬中應用提供技術支撐.

本文主要研究了貼體網格生成中邊界的離散技術，而在生成貼體網格時沒有考慮對內部網格步長控制和內部約束條件.受多旋回構造運動的影響，通常地下的地質條件復雜.受巖石巖性和流體特性的影響，地層呈非均質性.因此未來工作主要包括含有內部約束條件的貼體網格生成技術及貼體網格在地質地球物理中的應用.

Angeline P J.1998.Using selection to improve particle swarm optimization.∥IEEE World Congress on Computational Intelligence.USA：Anchorage Alaska，84-98.

Clerc M，Kennedy J.2002.The particle swarm explosion，stability，and convergence in a multidimensional complex space.IEEE Transactions on Evolutionary Computation，6（1）：58-73.

Dong G L.2005.Numerical simulation of seismic wave propagation under complex near surface conditions.Progress in Exploration Geophysics（in Chinese），28（3）：187-194.

Eberhart R C，Kennedy J.1995.A new optimizer using particle swarm theory.∥Proceedings of the Sixth International Symposium on Micro Machine and Human Science，Nagoya，Japan，39-43.

Gan Y，Qi C Q，Chen Y Z.2002.Smoothing of curves and surfaces based on genetic algorithm.Journal of Tongji University（in Chinese），30（3）：322-325.

Ji Z，Zhou J R，Liao H L，etal.2010.A novel intelligent single particle optimizer.Chinese Journal of Computers（in Chinese），33（3）：556-561.

Jiang L L，Sun J G.2008.Source terms of elliptic system in grid generation.Global Geology（in Chinese），27（3）：298-305.

Kennedy J，Eberhart R C.1995.Particle swarm optimization.∥Proceedings of the IEEE international Conference on Neural Networks.Perth，Australia：IEEE，4：1942-1948.

Kennedy J，Mendes R.2006.Neighborhood topologies in fully informed and best-of-neighborhood particle swarms.IEEE Transactions on Systems，Man，and Cybernetics，Part C：Applications and Reviews，36（4）：515-519.

Lan H Q，Liu J，Bai Z M.2011.Wave-field simulation in VTI media with irregular free surface.Chinese J.Geophys.（in Chinese），54（8）：2072-2084.

Lan H Q，Zhong J Z.2011.Three-dimensional wave-field simulation in heterogeneous transversely isotropic medium with irregular free surface.Bulletin of the Seismological Society of America，101（3）：1354-1370.

Liu Y F，Lan H Q.2012.Study on the numerical solutions of the eikonal equation in curvilinear coordinate system.Chinese J.Geophys.（in Chinese），55（6）：2014-2026.

Mei Z Y，Fan Y Q.2003.An algorithm for subdividing and approximating NURBS surface into quadrilateral mesh.Journal of Engineering Graphics（in Chinese），24（3）：105-110.

Mendes R，Kennedy J，Neves J.2004.The fully informed particle swarm：simpler，maybe better.IEEE Transactions on Evolutionary Computation，8（3）：204-210.

Shi Y H，Eberhart R C.1998.A modified particle swarm optimizer.∥Proceedings of the IEEE International Conference on Evolutionary Computation.Piscataway，NJ，USA：IEEE，69-73.

Sun J G，Jiang L L.2009.Orthogonal curvilinear grid generation technique used for numeric simulation of geophysical fields in undulating surface condition.Oil Geophysical Prospecting（in Chinese），44（4）：494-500.

Sun T，Tong X H.2010.A comprehensive curve error model based on broken-line approximation in curve position.Engineering of Surveying and Mapping（in Chinese），19（3）：26-30.

Sun X D，Li Z C，Wang X L.2012.Pre-stack reverse-time migration using a finite difference method based on triangular grids.Progress in Geophysics（in Chinese），27（5）：2077-2083.

Sun Z Q，Sun J G，Zhang D L.2009.2DDC Electric field numerical modeling including surface topography using coordinate transformation method.Journal of Jilin University：Earth Science Edition（in Chinese），39（3）：528-534.

Tao W Q.2001.Numerical Heat Transfer（Second Edition）（in Chinese）.Xi′an：Xi′an Jiaotong University Press.

Tian H，Xu N X，Mei G.2009.Method for optimizing hexahedral mesh of object with complex interpolation surfaces.Computer Engineering and Design（in Chinese），30（2）：286-290.

Wang X Q，Sun J G.2008.The state-of-the-art in numerical modeling including surface topography with finite-difference method.Progress in Geophysics（in Chinese），23（1）：40-48.

Wang Z L，Liu P Y，Cai H L.2007.Analysis of an optimizing calculation of no-round curve by beeline approximation.Machinery Design ＆Manufacture（in Chinese），（9）：176-178.

Wu F M，Pan R J.2011.Surface fairing based on energy optimization and nonuniform B-spline wavelets.Computer Engineering and Applications（in Chinese），47（18）：176-178，185.

Yang X D，Qiao Z D，Zhu B.2002.An easily generated and highquality grid generation method for aircraft configuration.Journal of Northwestern Polytechnical University（in Chinese），20（1）：49-53.

Yu R X，Zhu Z Q.2003.Transfinite interpolation grid generation with the application of B spline.Journal of Beijing University of Aeronautics and Astronautics，29（1）：27-30.

Zhong Y Q，Wang Y P，Wang K W.2011.Biarc approximation of freeform curves based on particle swarm optimization algorithm.China Mechanical Engineering（in Chinese），22（21）：2530-2535.

Zhu D L，Bai C Y.2011.Review on the seismic wavefield forward modelling.Progress in Geophysics（in Chinese），26（5）：1588-1599.

Zhu X X.2001.Free curve and surface modeling techniques（in Chinese）.Beijing：Science Press.

附中文參考文獻

董良國.2005.復雜地表條件下地震波傳播數值模擬.勘探地球物理進展，28（3）：187-194.

甘屹，齊從謙，陳亞洲.2002.基于遺傳算法的曲線曲面光順.同濟大學學報，30（3）：322-325.

紀震，周家銳，廖惠連等.2010.智能單粒子優化算法.計算機學報，33（3）：556-561.

蔣麗麗，孫建國.2008.基于Poisson方程的曲網格生成技術.世界地質，27（3）：298-305.

蘭海強，劉佳，白志明.2011.VTI介質起伏地表地震波場模擬.地球物理學報，54（8）：2072-2084.

劉一峰，蘭海強.2012.曲線坐標系程函方程的求解方法研究.地球物理學報，55（6）：2014-2026.

梅中義，范玉青.2003.NURBS曲面的四邊形網格的分割與逼近.工程圖學學報，24（3）：105-110.

孫建國，蔣麗麗.2009.用于起伏地表條件下地球物理場數值模擬的正交曲網格生成技術.石油地球物理勘探，44（4）：494-500.

孫彤，童小華.2010.基于折線逼近的曲線位置與模型誤差綜合建模.測繪工程，19（3）：26-30.

孫小東，李振春，王小六.2012.三角網格有限差分法疊前逆時偏移方法研究.地球物理學進展，27（5）：2077-2083.

孫章慶，孫建國，張東良.2009.二維起伏地表條件下坐標變換法直流電場數值模擬.吉林大學學報：地球科學版，39（3）：528-534.

陶文銓.2001.數值傳熱學（第二版）.西安：西安交通大學出版社.

田紅，徐能雄，梅鋼.2009.含復雜插值曲面實體六面體網格優化方法.計算機工程與設計，30（2）：286-290.

王雪秋，孫建國.2008.地震波有限差分數值模擬框架下的起伏地表處理方法綜述.地球物理學進展，23（1）：40-48.

王振祿，劉鵬玉，蔡慧林.2007.直線逼近非圓曲線的優化算法.機械設計與制造，（9）：176-178.

吳福鳴，潘日晶.2011.基于能量優化與非均勻B樣條小波的曲面光順.計算機工程與應用，47（18）：176-178，185.

楊旭東，喬志德，朱兵.2002.一種改進的四邊界插值網格生成方法及其應用.西北工業大學學報，20（1）：49-53.

吁日新，朱自強.2003.B樣條應用于超限插值的網格生成方法.北京航空航天大學學報，29（1）：27-30.

鄭永前，王云鵬，王科委.2011.基于粒子群優化算法的自由曲線雙圓弧逼近.中國機械工程，22（21）：2530-2535.

朱多林，白超英.2011.基于波動方程理論的地震波場數值模擬方法綜述.地球物理學進展，26（5）：1588-1599.

朱心雄.2001.自由曲線曲面造型技術.北京：科學出版社.