一種新的大載波頻偏估計算法

聶少軍，何兵哲，王宏卓

（中國空間技術研究院西安分院 陜西 西安 710100）

在衛星擴頻通信系統中，接收機接收到衛星的下行信號，經過射頻前端濾波放大后，再下變頻到中頻，最后經AD采樣后形成數字中頻信號，進入基帶處理單元。由于多普勒效應的影響，數字化后的中頻信號的載波頻率存在著較大的偏移。對于包含頻偏和各種噪聲的中頻數字信號，其處理可分為捕獲和跟蹤兩個階段。捕獲成功后得到粗略的載波和碼相位估計值。這些估計值被送入跟蹤環路，跟蹤環路由載波跟蹤環和碼延遲鎖定環組成。跟蹤環路產生更精確的載波和碼相位估計值，并解調接收數據。其中捕獲過程獲得的碼相位估計誤差在半個碼片以內，載波頻率誤差在半個搜索步長內[1]。

1 載波搜索步長對同步性能的影響

圖1 載波頻偏對擴頻碼相關值的影響Fig.1 Influence of carrier frequency offset on the spread spectrum code correlation value

當接收信號的碼相位與本地碼的碼相位精確對準時，相關器輸出信號的包絡為[2]：

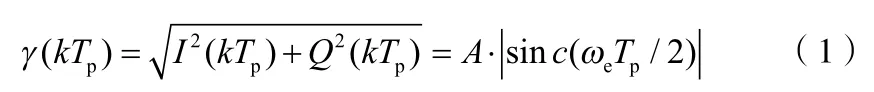
式中A為A/D后的輸入信號幅度，ωe為載波頻率估計誤差，Tp為預檢測積分時間。可見殘余的載波頻差會使相關峰值產生| sinc(ωeTP/2) |倍衰減。隨著頻差的增大，相關值將越來越小，最終導致捕獲失敗。令測距碼測碼長L=210-1 chips，碼速率RPN=10.23 Mcps ，預檢測積分時間Tp =0.1 ms，仿真可得測距碼自相關峰值與載波頻偏的關系如圖1所示。

由圖1可見，在沒有頻偏時（Δf =0），歸一化相關峰為1，而且相關值會隨Δf的增加迅速下降。在載波頻差較低的時候，相關峰幅值的減小降低了捕獲概率，增加了捕獲時間；在載波頻差比較大的時候，相關峰的幅度急劇降低，捕獲失敗的風險急劇上升。頻率搜索步長和擴頻碼的捕獲密切相關，頻率估計誤差影響相關累加結果。

與此同時，為了準確地解調數據，減小熱噪聲對跟蹤精度的影響，一般跟蹤環路的噪聲帶寬都很窄[3]。典型的載波跟蹤環的帶寬小于50 Hz，碼跟蹤環的帶寬一般只有2 Hz左右[4]。綜合上述原因，載波的搜索步長應盡可能的小，以保證捕獲頻率能夠使載波環入鎖。但過小的步長導致頻率搜索單元過多，搜索時間過長。一般而言，搜索步長都在500 Hz以上[5]。

2 剩余載波頻差估計算法

從以上分析可以看出，擴頻碼捕獲后，雖然通過頻率搜索確定了大致的載波頻率范圍，但剩余的載波頻差還很大（最大fstep/2），而跟蹤環路需要更精確的載波估計值。令接收信號為：

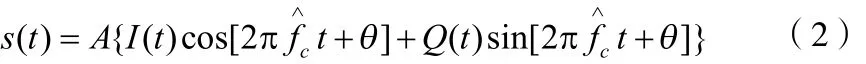
其中I(t)、Q(t)為二進制的發送數據， 為發送信號載波頻率。經正交下變頻后得到的同相分量、正交分量分別為：

其中fc為接收信號的載波頻率。分別對同相分量和正交分量延時τ得到：

基于反余弦函數的載波頻差估計算法原理框圖如圖2所示[6]。

3 仿真與結果分析

令載波頻率fc=2.3 GHz，采樣頻率fc=60 MHz，積分時間T=1 ms，仿真時間0.5 s，信噪比-20 dB ，延時長度τ=1 000/fs。考察載波頻差從-5 kHz到+5 kHz時的剩余頻率誤差估計結果，得其頻差估計如圖3所示。

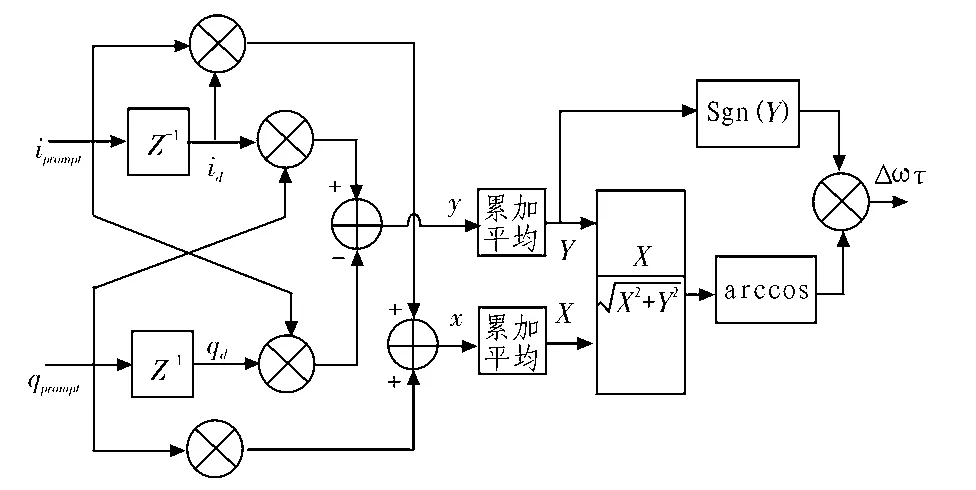
圖2 基于反余弦函數的載波頻差估計算法框圖Fig.2 Structure diagram of the estimate algorithm of carrier frequency offset based on the arcos function

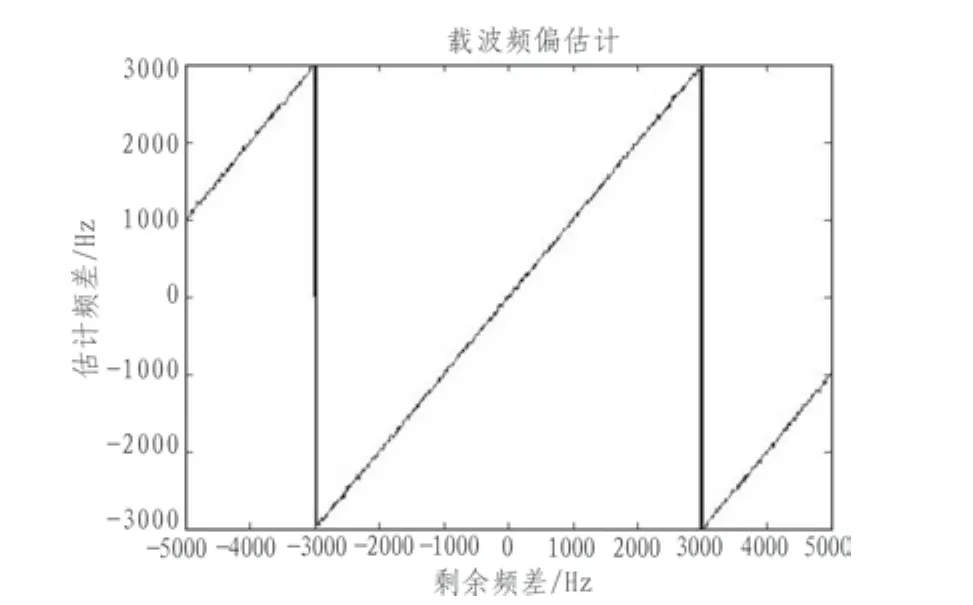
圖3 基于反余弦函數的載波頻差估計結果Fig.3 Estimation of the carrier frequency offset based on the arcos function

由圖3可以看出，剩余頻率誤差估計的線性區域為-3～+3 kHz。超出這個區間后估計結果出現了振蕩。這主要是受限于延時長度的大小。由式（9）可得：

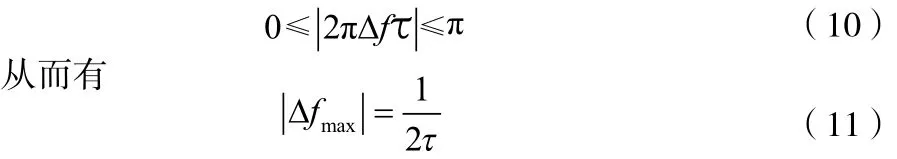
在上述仿真參數下，考察其線性區域內的估計性能。令載波頻差的范圍為-1.5 ～ +1.5 kHz。觀察其頻差估計結果、估計絕對誤差、估計相對誤差，得圖4 ～圖6。

由圖4可以看出，剩余頻率誤差估計效果較好，能較為準確的估計載波頻率經過捕獲后剩余的誤差。

圖4 線性區域內的載波頻差估計結果Fig.4 Estimation of the carrier frequency offset in the linear region

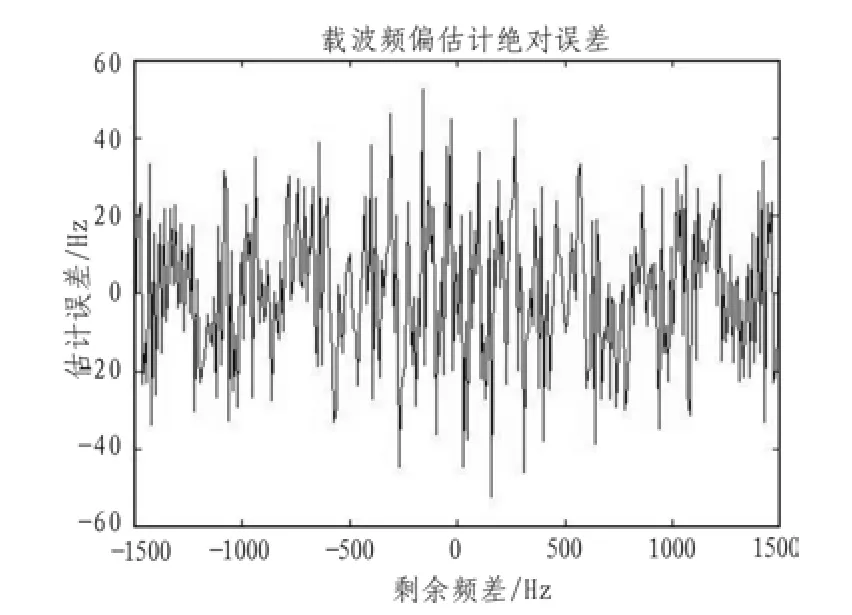
圖5 基于反余弦函數的載波頻差估計絕對誤差Fig.5 Absolute error of the carrier frequency offset estimation based on the arcos function

由圖5可以看出，頻率估計誤差在-60～60 Hz之間，載波頻率誤差和估計之前的粗捕值相比，下降了一個數量級。由圖6可以看出，在剩余頻差較大時，相對估計誤差很小，估計效果好。在剩余頻差接近0的時候，估計結果出現了相對較大的波動。但是考慮到其絕對值在幾赫茲到十幾赫茲之間，已經進入載波鎖相環的跟蹤范圍。更精確的頻差估計可交給載波跟蹤環路。

4 結束語

文中首先給出了衛星擴頻通信系統的載波同步過程，指出了載波[7-8]捕獲的剩余頻差對系統同步性能的影響。載波同步過程存在著同步速度和同步準確性的矛盾。然后通過理論推導，提出了基于反余弦函數的算法，來估計經過粗捕獲后的剩余載波頻差。最后經過仿真表明該具有良好的抗噪聲性，估計范圍大，估計精度較高，而且該算法易于實現，具有良好的特性。

[1]姜昌, 范曉玲. 航天通信跟蹤技術導論[M].北京:北京工業大學出版社, 2003.

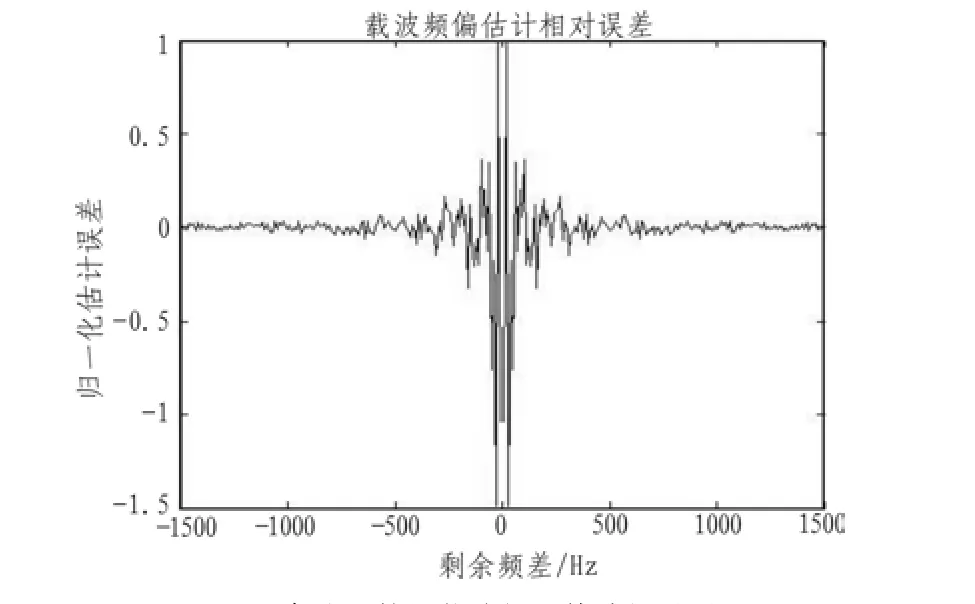
圖6 基于反余弦函數的載波頻差估計相對誤差Fig.6 Comparative error of the carrier frequency offset estimation based on the arcos function

[2]Kaplan E, Hegarty C J. GPS原理與應用[M]. 2版. 寇艷紅,譯.北京:電子工業出版社,2007.

[3]王琦,吳斌. 航天測控系統中偽碼測距精度分析[J]. 無線電工程,2009(1):39-44.

WANG Qi, WU Bin. Analysis on precision of pseudo noise code ranging in space TT&C systems [J]. Radio Engineering, 2009 (1):39-44.

[4]柴俊栓,張曉輝.GPS接收機載波跟蹤環設計與分析[J]. 電子設計工程,2012(8):118-121.

CHAI Jun-shuan, ZHANG Xiao-hui. Design and analyzing of carrier tracking loop for GPS receiver [J]. Electronic Design Engineering, 2012 (8):118-121.

[5]魯郁. GPS全球定位接收機-原理與軟件實現[M].北京:電子工業出版社, 2009.

[6]宋育楓, 李志強, 張偉. 一種基于反余弦函數的大載波頻偏估計算法[J]. 軍事通信技術,2004(4):12-15.

SONG Yu-feng, LI Zhi-qiang, ZHANG Wei. Practical AFC algorithm based on arcos function [J]. Journal of Military Communications Technology, 2004(4):12-15.

[7]黃富彪，何兵哲.一種衛星信號載波頻率精確估計算法[J].現代電子技術，2013(3):129-131,134.

HUANG Fu-biao，HE Bing-zhe.A carrier frequency accurate estimation algorithm for satellite signal[J].Modern Electronics Technique，2013(3):129-131,134.

[8]張超，馮玉峰，孫學君.基于電力線載波通信的油井通信系統[J].電子科技，2012(3):93-96,100.

ZHANG Chao，FENG Yu-feng，SUN Xue-jun.Oil well communication system based on the power line carrier communication[J]. Electronic Science and Technology, 2012(3):93-96,100.