基于視覺信息的無人機自主著陸過程姿態角簡化計算方法
曾志遠,許瑛
(1.南昌航空大學航空制造工程學院,江西 南昌 330063;2.南昌航空大學飛行器工程學院,江西 南昌 330063)
0 引言
無人機自主著陸是無人機研究中的難點之一。為了能夠實現自主著陸,無人機必須具備自主導航的能力[1-2]。目前,無人機的自主導航技術主要有慣性導航和GPS導航等。其中,慣性導航在給定了初始條件后,不需要外部參照就可確定當前位置、方向及速度,不受到外界的影響,但其定位誤差是隨時間積累的累積誤差,精度受到慣導系統的影響且無法單獨使用;GPS導航能夠全天候提供準確的定位,但其容易受到電磁干擾,所以GPS導航并不是嚴格意義下的自主導航[3-5]。隨著計算機視覺技術和攝像機硬件的發展,視覺導航由于其完全自主且無源等特點被越來越多地應用在無人機自主著陸的研究中。在視覺導航中,很多研究者采用地平線算法來估算無人機的姿態角[1,6-7]。他們首先假設無人機的 bybzb平面與攝像機的像平面平行,然后通過獲得的地平線的參數可以得到無人機的滾轉角和俯仰角。在獲得滾轉角和俯仰角的前提下,通過圖像中的跑道的兩條邊界直線可以確定無人機的偏航角。采用此種方法,對攝像機的安裝位置有一定的限制。
本文提出了一種無人機姿態角估算方法。首先,在無人機獲得跑道圖像后,通過視覺系統提取出跑道和地平線特征,對攝像機的姿態角進行估算;然后,通過矩陣轉換求得無人機的姿態角。該方法不用確保無人機的bybzb平面與攝像機的像平面平行,攝像機的位置可以任意安裝而不受到限制。
1 視覺導航系統原理
采用視覺導航技術實現無人機自主著陸必須用到攝像機。因為攝像機的作用是用來拍攝無人機著陸過程中圖像的,所以除了設計要求外,對攝像機的安裝位置沒有其他要求。伴隨著無人機的著陸,無人機上的攝像機會拍攝到著陸過程中的一系列圖像。研究所拍攝到的圖像特征后,我們發現圖像中主要包括了天空、跑道和跑道周圍的景物,而且圖像中顯著的兩個特征是地平線和跑道的邊界線。
攝像機獲取圖像后,首先進行圖像分割,將數字圖像細分為多個像素的集合,這樣可以簡化圖像的表示形式,使圖像更容易理解和分析。然后對圖像中的地平線和跑道特征進行提取,接著就可以根據提取出來的特征,對無人機的姿態角進行估算。如圖1所示。

圖1 圖像處理過程
2 無人機坐標系的建立
無人機的坐標系統如圖2所示。g為絕對坐標系的原點,xg軸的方向與跑道中心線方向相同,zg軸與跑道平面垂直且方向向下,yg軸與xg,zg軸滿足右手定則;b為無人機機體坐標系的原點,bxb軸與gxgyg平面的夾角即為俯仰角,bxb軸在gxgyg平面的投影與gxg的夾角即為偏航角,bzb軸與包含bxb軸的鉛垂平面的夾角即為滾轉角;c為攝像機坐標系的原點,xc軸與攝像機光軸平行;D為跑道上任意一點。
3 攝像機姿態角的計算
3.1 滾轉角的計算
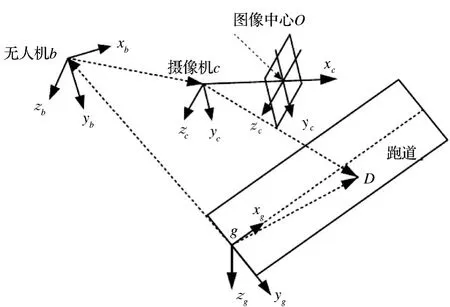
圖2 無人機坐標系
建立如圖3所示的像平面坐標系,圖中直線H為對相片進行圖像處理后得到的地平線,平面V為過軸xc且與地平線H垂直的平面。由滾轉角的定義,滾轉角為Ozc軸與包含Oxc軸的鉛垂平面的夾角,方向與Oxc軸方向一致,右滾轉為正。所以,圖中角φc即為所求的滾轉角,大小為地平線H與yc軸的夾角或與yc軸平行的像平面一條邊的夾角。

圖3 攝像機滾轉角
3.2 俯仰角計算
圖3中,地平線H用參數 (φc,σ)來表示。其中,φc為地平線H相對于所得圖像中yc軸的角度,φc的范圍為σ表示地平線以上的圖像面積占整個圖像面積的百分比,范圍為0%~100%。
對于俯仰角的估算,從圖像中提取出來的跑道特征來估算攝像機的俯仰角[8]:

式中:W為圖像中的縱向像素點的數目;dy為一個像素的縱向長度;f為攝像機的焦距;r為地球半徑;h為無人機進場時的初始高度。
3.3 偏航角估算
在圖3中,像中心O的坐標為 (Ou,Ov),圖像中滅點I'的坐標為 (I'u,I'v)。將I'點繞O點旋轉一滾轉角 φ 得到 I″,坐標為 (I″u,I″v),h'為 I″到 O 點的距離[9]。則估算方法如下:
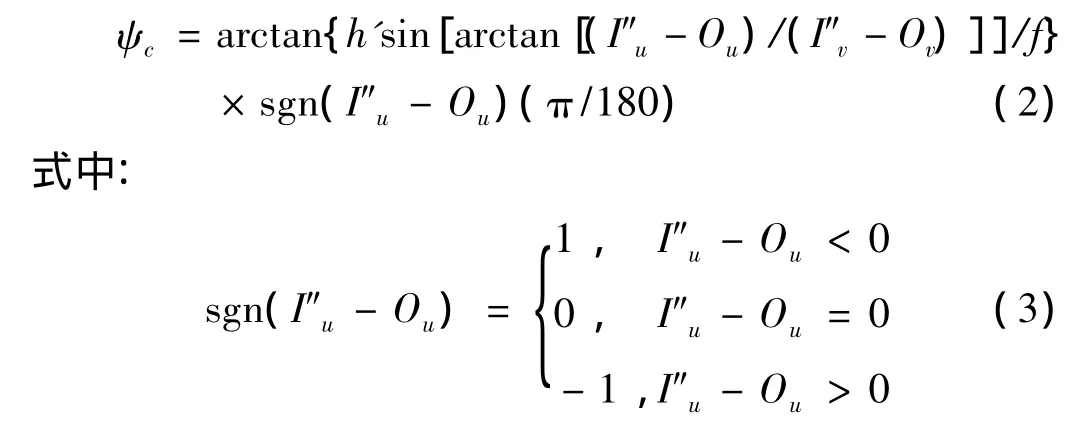
4 飛機姿態角的計算
根據前文已經估算出的攝像機的三個姿態角φc,θc,ψc,代入公式 (4)就可以求出地面坐標系到攝像機坐標系的轉換矩陣Sc/g,結果為
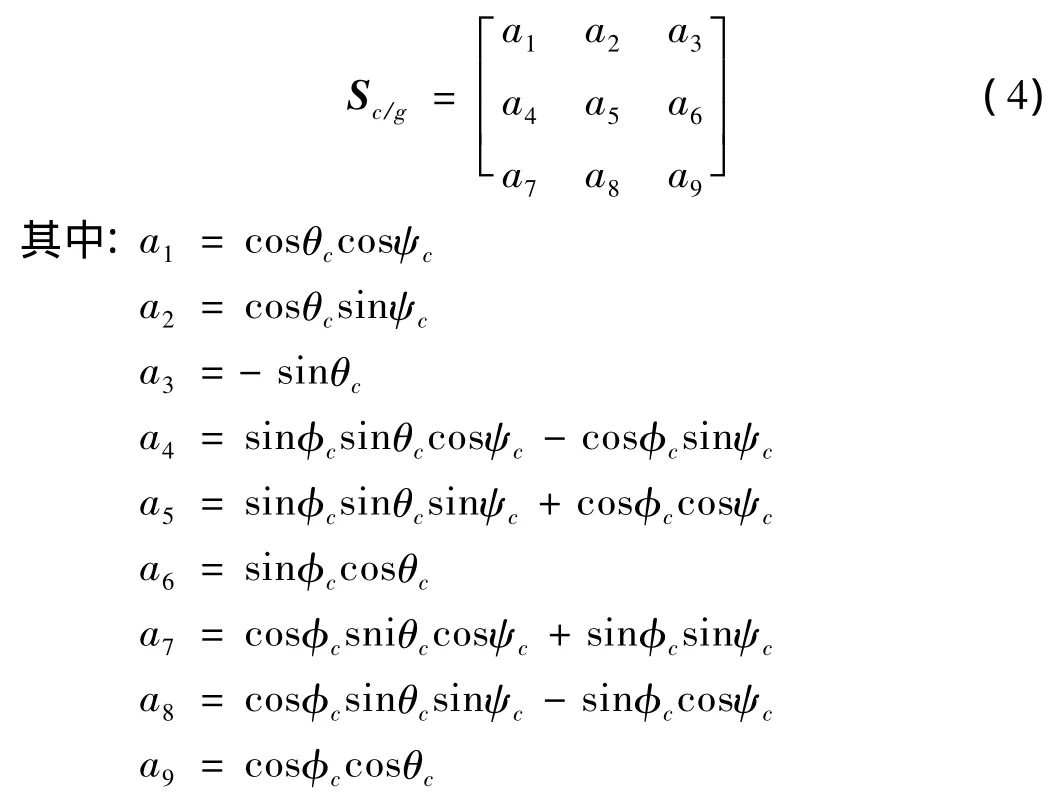
當攝像機固定在無人機上時,攝像機的坐標系相對于無人機坐標系的位置是固定的,因此攝像機坐標系在無人機坐標系下的姿態角:滾轉角φc/b,俯仰角θc/b和偏航角ψc/b為固定值。由此可以得到無人機坐標系到攝像機坐標系的變換矩陣為常數矩陣Sc/b。表示為
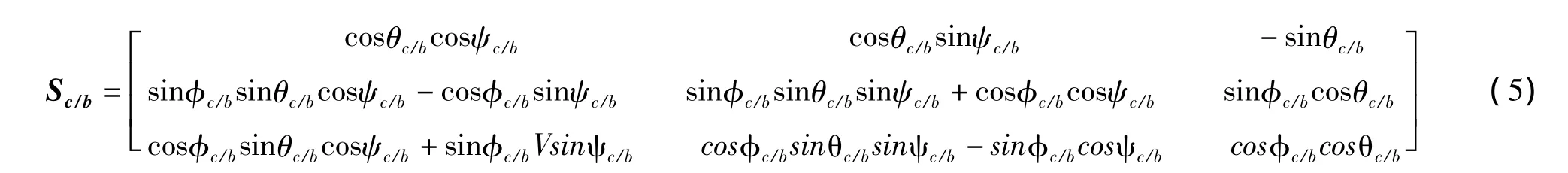
變換矩陣之間存在著如下關系:

把式 (4)求出的地面坐標系到攝像機坐標系的轉換矩陣Sc/g和常數矩陣Sc/b代入到式 (6)中,即可求出機體坐標系到地面坐標系的變換矩陣Sb/g。可以表示為
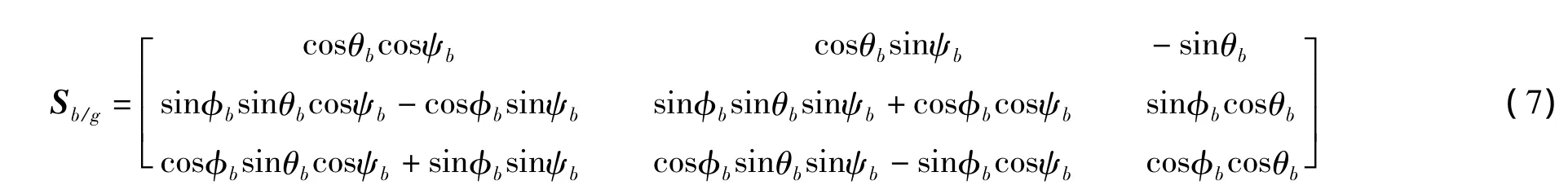
很容易看出,矩陣中第一行和第三列之間存在如下的關系:
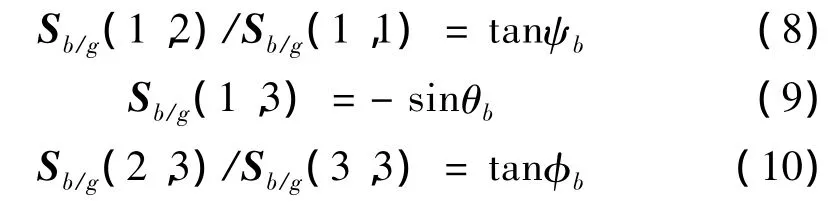
由公式 (8)、公式 (9)和公式 (10)可以得到無人機的偏航角,俯仰角和滾轉角的估算式,其結果為
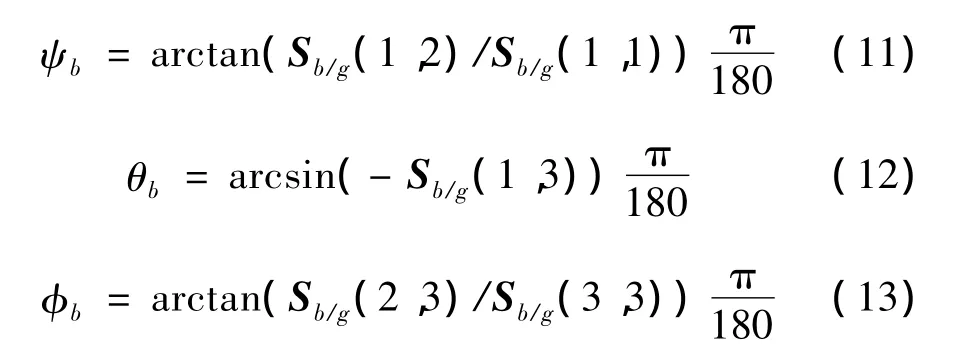
所以,求出機體坐標系到地面坐標系的變換矩陣Sb/g,然后把Sb/g中的元素代入式 (11)、式 (12)和式 (13)中,即可估算出無人機的三個姿態角。
5 算例驗證
無人機獲取跑道的圖像后,首先提取出圖像中的地平線和跑道的特征方程如表1所示。

表1 提取出的直線方程
其中,圖像大小為300 mm×200 mm,f=9 mm,一個像素在圖像物理坐標系中的尺寸為dx=dy=0.034 mm。把已經獲得的數據代入到上面的算法中,使用Matlab 2012a即可分別求出無人機的三個姿態角,如表2所示。
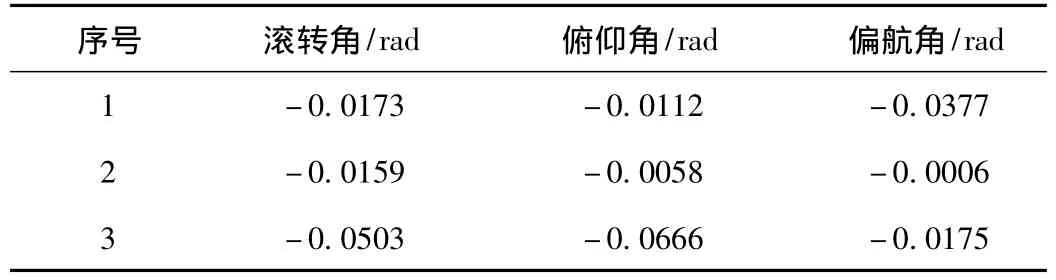
表2 姿態角計算結果
6 結束語
本文提出了一種無人機自主著陸過程中姿態角的估算方法,結合矩陣變換對地平線算法進行了改進,與改進前算法相比,此算法對攝像機安裝位置沒有特殊的要求。仿真計算結果證明其能估算出無人機的姿態角,并且具有更好的適應性。
[1]Lin Xinhua,Cao Yunfeng.Research on the application of vision-based autonomous navigation to the landing of the UAV[J].Proc.SPIE Int.Soc.Opt.Eng,2003,5253:385–388.
[2]沈寧,唐大全,李飛.無人機視覺導航中的圖像處理及位姿解算 [J].光電技術應用,2012,27(6):60-64.
[3]Doehler H U,Korn B R.Autonomous infrared-based guidance system for approach and landing [J].Proc.SPIE,2004,5424:140-147.
[4]Tang Daquan,Zhang Hongyue.Vision Based Navigation Algorithm for Autonomic Landing of UAV without Heading&Attitude Sensors[C]//3th International IEEE Conference on Signal-Image Technologies and Internet-Based System.[S.l.]:IEEE,2008:972-978.
[5]付丙島,丁文銳,王廣彪,等.用于飛行器視覺導航的地平線檢測算法 [J].北京航空航天大學學報,2011,37(7):849-854.
[6]Saripalli S,Montgomery J F,Sukhatme G S.Vision-based Autonomous Landing of an Unmanned Aerial Vehicle[C]//Proceeding of IEEE International Conference on Robotics and Automation.Washington:IEEE,2002:2799-2804.
[7]劉新華.基于視覺的無人機著陸姿態檢測和跑道識別[D].南京:南京航空航天大學,2004.
[8]劉興華,曹云峰,劉新華.計算機視覺在無人機著陸中的應用 [J].航空計測技術,2004,24(6):1-3.
[9]李紅,柴洪林,彭嘉雄.基于視覺的無人機姿態角估計[J].華中科技大學學報:自然科學版,2007,35(6):4-7.

