一類RN上奇異擬線性橢圓方程非平凡解的不存在性

劉曉，李嵐，陳才生

（1.河海大學(xué)理學(xué)院，江蘇南京 211100；2.中國交通通信信息中心北京，100011）

一類RN上奇異擬線性橢圓方程非平凡解的不存在性

劉曉1，李嵐2，陳才生1

（1.河海大學(xué)理學(xué)院，江蘇南京 211100；2.中國交通通信信息中心北京，100011）

主要研究一類奇異擬線性橢圓型方程非平凡解的不存在性.利用變分法，通過建立一個(gè)Pohozaev型的變分恒等式，并對權(quán)函數(shù)以及參數(shù)適當(dāng)假設(shè)，得到這類問題只有零解的充分條件.

奇異擬線性橢圓方程；變分法；不存在性；變分恒等式

MSC2010：35J62；35J75

由于擬線性橢圓方程有著強(qiáng)大的物理背景以及實(shí)際應(yīng)用價(jià)值，如在流體力學(xué)、牛頓流體、滲透力學(xué)等物理模型［1－4］中的應(yīng)用，所以對于它的研究也備受國內(nèi)外學(xué)者的青睞.對于擬線性橢圓問題解的存在性，已經(jīng)吸引了相當(dāng)一部分研究人員.宣本金［5］討論了下列問題

蘇加寶等［6－13］研究了擬線性橢圓問題

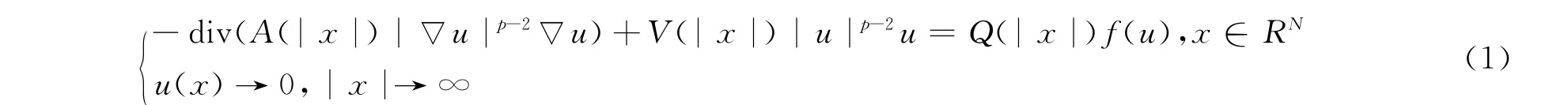
的非平凡徑向解的存在性.其中，A（r），V（r）和Q（r）是正的徑向?qū)ΨQ函數(shù).通過對A，V和Q在r＝0和r＝∞時(shí)的適當(dāng)假設(shè)，證明了嵌入X＝W1，pr（RN，A，V）→Lq（RN，Q）是緊的，并且進(jìn)一步證明了上述問題在空間X中存在徑向解.

但有關(guān)上述問題解的不存在性結(jié)果很少.

1 主要定理

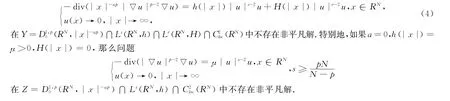
2 主要結(jié)論

3 討論

本文與大多數(shù)文獻(xiàn)不同之處在于是從解的不存在性的角度來進(jìn)行討論的.利用變分法，討論了一類p-laplacian方程在全空間RN上非平凡解的不存在性，即只有零解.

在問題（2）中，通過令權(quán)函數(shù)V（x），H（x）∈C1loc（0，∞），以及α，β∈R1并滿足（A1）、（A2），可以得到問題（3）在X中只有零解；令權(quán)函數(shù)h（x），H（x）∈C1loc（0，∞），以及α，β∈R1并滿足（A3）、（A4），那么問題（4）在Y中只有零解.在證明這2個(gè)結(jié)論的過程中，將Pohozaev恒等式作了進(jìn)一步的推廣，所得的結(jié)果對于豐富非線性橢圓型方程的學(xué)術(shù)研究具有很大的意義.

但是注意到，本文中對權(quán)函數(shù)h（x），V（x），H（x）以及空間X，Y的限制比較多，若將權(quán)函數(shù)的條件減弱，或者將空間X，Y放大，結(jié)論是否仍然成立有待進(jìn)一步研究.

［1］ ASSUNC ORB，CARRI OPC，MIYAGAKI O H.Subcritical perturbations of a singular quasilinear elliptic equation involving the critical Hardy-Sobolev exponent［J］.Nonlinear Anal，2007，66：1351-1464.

［2］ BROCK F，ITURRIAGA L，S NCHEZ J，et al.Existence of positive solutions for p-Laplacian problems with weights［J］.Commun on Pure and Appl Anal，2006，5（4）：941-952.

［3］ GHERGU M，R DULESCUV.Singular elliptic problems with lack of compactness［J］.Annali di Matematica，2006，185：63-79.

［4］ XUAN Benjin.The solvability of quasilinear Brezis-Nirenberg-type problems with singular weights［J］.Nonlinear Anal，2005，62：703-725.

［5］ XUAN Benjin，WANG Ji.Existence of a nontrival weak solution to quasilinear elliptic equations with singular weights and multiple critical exponents［J］.Nonlinear Anal，2010，72：3649-3658.

［6］ SU Jiabao，WANG Zhiqiang.Sobolev type embedding and quasilinear elliptic equations with radial potentials［J］.J Differential Equations，2011，250：223-242.

［7］ BERESTYCKI，LIONS H P L.Nonlinear scalar field equations，I.Existence of a ground state［J］.Arch Rational Mech Anal，1983，82：313-345.

［8］ DING Weiyue，NI Weiming.On the existence of positive entire solutions of a semilinear elliptic equa-tion［J］.Arch Rational Mech Anal，1986，91：283-308.

［9］ FURUSHO Y，TAKASI K，OGATA A.Symmetric positive solutions of second-order quasilinear degenerate elliptic equations［J］.Arch Rational Mech Anal，1994，127：231-254.

［10］ NOUSSAIR E S，SWANSON C A，YANG Jianfu.Quasilinear elliptic problem with critical exponents［J］.Nonlinear Anal，1993，20：285-301.

［11］ RODRIGUES R S.On elliptic problems′involving critical Hardy-Sobolev exponents and sign-changing function［J］.Nonlinear Anal，2010，73：857-880.

［12］ TERAMO T.On positive radial entire solutions of second-order quasilinear elliptic systems［J］.J Math Anal Appl，2003，282：531-552.

［13］ YU Laosen.Nonlinear p-Laplacian problems on unbounded domains［J］.Proc Amer Math Soc，1992，115（4）：1037-1045.

［14］ C STEA F，MOTREANU D，R DULESCUV.Weaksolutionsofquasilinear problems with nonlinear boundary condition［J］.Nonlinear Anal，2001，43：623-636.

［15］ DAUTRAY R，LIONS J L.Mathematical analysis and numerical methods for science and technology［M］.Berlin：Springer-verlag，1990.

［16］ KUZIN I，POHOZAEV S.Entire solutions of semilinear elliptic equations［M］.Berlin：Birkh auser，1997.

（責(zé)任編輯：王蘭英）

Nonexistence of nontrivial solution of a class of singular quasilinear elliptic problem on RN

LIU Xiao1，LI Lan2，CHEN Caisheng1
（Department of Mathematics，Hohai University，Nanjing 211100，China；
2.China Transport Telecommunications and Information Center，Beijing 100011，China）

The nonexistence of solution of a class of singular quasilinear elliptic problem was studied.Under the appropriate assumptions，on the weight functions and the parameters，a Pohozaev＇s variational identity is given by using variational methods.It implies the nonexistence of nontrivial solution.

singular quasilinear elliptic equation；variational methods；nonexistence；variational identity

O175.25

A

1000-1565（2014）05-0449-06

10.3969／j.issn.1000-1565.2014.05.001

2013-07-15

國家自然科學(xué)基金資助項(xiàng)目（11201115）

劉曉（1991-），女，山東莒南人，河海大學(xué)在讀碩士研究生，主要從事偏微分方程方向研究.E-mail：xiao＿123987＠126.com