小波基預測函數控制在陶瓷燒成溫度控制中的應用*
侯 寧 費樹岷
(1 江蘇開放大學 江蘇 無錫 214011)(2 東南大學自動化學院 南京 210096)
陶瓷燒成窯爐是陶瓷生產過程最主要的設備,是生產過程的“心臟”,對提高陶瓷產品的品質起著決定性的作用。但是由于陶瓷燒成窯爐具有大純滯后的特征,并且控制關系具有非線性,系統與控制指標(如溫度,氣氛,壓力)之間為較強耦合,又表現為不確定性,普通的控制策略很難對其實現有效控制。為此一些針對陶瓷燒成窯爐控制策略被提出,文獻[1]提出變結構溫度控制方法,即通過模糊控制和時間比例分割相結合應用于陶瓷燒成窯爐中,并證明控制方法是有效的;文獻[2~4]將智能控制與PID控制技術相融合,通過整合兩種控制思想形成了模糊PID控制器的設計方法,對窯爐各工作區的溫度的調節是可行的;文獻[5]通過模糊控制和預測控制2種策略的結合來控制燒成溫度,在精度和快速性方面取得較好的效果。文獻[6]通過RBF神經網絡建立對窯爐的溫度特性進行建模,解決了用普通控制算法建立非線性對象精確模型的問題,并結合動態矩陣預測控制實現對溫度變化的跟蹤控制;文獻[7]將窯爐內的溫度偏差及偏差變化率通過智能邏輯控制器得到控制信號,實現燒成溫度的智能控制。
預測函數控制(Predictive Functional Control, 簡稱PFC)是第三代模型預測控制算法,由J Richalet于1986年提出[8],廣泛應用于機器人跟蹤、雷達跟蹤、熱焓控制等領域[9~14]。該方法的特點是在控制量的結構中加入了基函數的內容,基函數的形式以及數量可以根據控制過程預先選定,控制量的解析解為與基函數相關的線性組合,各基函數作用系統形成的輸出為加權組合結構,通過目標函數的優化得到加權系數。在普通PFC控制方法中,基函數一般可取階躍函數、斜坡函數、指數函數以及正弦多項式函數等。這類基函數結構簡單,離線計算方便,不足的是以上函數都是全局函數,對信號的逼近不能根據信號的局部特征即不同逼近精度而靈活設置,難以達到預期的控制效果[15]。筆者提出一種基于小波基函數的陶瓷燒成窯溫度預測函數控制方法,仿真結果表明該方法的有效性。
1 陶瓷燒成窯爐溫度預測函數控制
根據控制系統的要求,對陶瓷燒成溫度進行控制,要求控制過程輸出即燒成溫度能夠快、準、穩地達到設定溫度值。
1.1 陶瓷燒成窯爐數學模型[16]
為了獲得陶瓷燒成窯爐數學模型,可以從數學途徑分析其工藝過程,寫出有關的數學關系表達式,然后推導出被控對象的模型。作為具有代表性的生產過程,陶瓷燒成窯爐模型可表示為以下常見工業過程:
(1)
式中:K——比例常數;
τ——時延時間;
T——過程時間常數。
式(1)表示的是一階慣性加純滯后模型。當式中τ與T的比值大于0.3時,稱為大純滯后慣性環節;當比值小于0.3時,稱為一般純滯后慣性環節。筆者在對象數學模型的仿真過程中取K=5,τ=10,T=20,即大純滯后慣性環節。
1.2 控制輸入與模型輸出
預測函數控制方法在控制量的結構中加入了基函數的內容,控制量為:
(2)
式中:μj——線性組合的加權系數;
fbj(i)——基函數在t=iT時的取值;
nB——基函數的個數;
h——預測優化時域的長度。
陶瓷燒成溫度預測函數控制的模型輸出ym(k+i)可以表示為:
ym(k+i)=yU(k+i)+yF(k+i)
(3)
式中:yU——自由(unforced)響應輸出,即為輸入控制為零情況下模型的響應;
yF——由式(2)所給的新增控制輸入作用下的強迫響應,可以由下式得到:
(4)
式中:ybj(i)為過程在第j個基函數fbj(i)作用下的模型輸出,不需要在線計算出;加權系數μj(k)可以通過在線求解得到。
陶瓷燒成溫度預測函數控制的預測模型為:
Xm(k)=EmXm(k-1)+Fmu(k-1)
ym(k)=CmXm(k)
(5)
式中:Xm∈Rn*1——狀態向量;
u∈R1*1——控制輸入;
ym∈R1*1——預測模型輸出;
Em∈Rn*n、Fm∈Rn*1、Cm∈R1*n——分別是模型的系數或向量。
由式(2)、(3)、(4)、(5)得到:
ym(k+1)=CmXm(k+i)
(6)
式中:μ(k)=[μ1(k),μ2(k),L,μnB(k)]T;
yb(i)=[yb1(k),yb2(k),L,ybnB(k)]T。
1.3 控制系統參考軌跡
為了達到預期的控制目標,系統的模型輸出在控制過程中要能跟蹤參考軌跡,從而使系統控制溫度能夠平穩的達到預期溫度值(設定值)。預測函數控制的參考軌跡在形式上沒有特別限制,筆者選取以下指數形式作為過程跟蹤參考軌跡,其表達式為:
(7)
式中:yR(k+1)——k+i時刻參考軌跡的值;
s(k)——設定溫度值軌跡;
yp——實際過程輸出;

sb(k)——多項式系數;
Bs——表示多項式階數。
1.4 誤差補償與優化計算
對于過程輸出與模型輸出之間的誤差問題,通過反饋進行未來誤差的預測和補償,通常取未來誤差為:
(8)
式中:et(k)和Be分別為多項式的系數和階數。
(9)
預測函數控制方法中控制量是通過優化實現的。具體做法是在預測時域上取若干優化點,使得優化目標函數表達式為:
(10)
式中:nh——擬合點的個數,且nh≥nB;
hj——第j個擬合點的值,即為介于優化時域之間的一些離散點。求 ?J/?μ(k)=0,求解出[μ1(k),μ2(k),KμnB(k)]后,通過式(2)可得到控制量的解析式。
針對式(1)所示的一階慣性加純滯后系統,在τ=0模型上進行修正,思路如下:
ypa(k)=ym(k)+yp(k)-ym(k+D)
(11)

設跟蹤預期溫度值為階躍設定值,則s(k+i)=s(k),經優化計算可得到k時刻的控制量:
(12)
式中各系數:
式中:A=(GGT)-1G;
G=[yb(h1),yb(h2),K,yb(hnh];
yb(i)=[yb1(k),yb2(k),K,ybnB(k);
fb(0)=[fb1(0),fb2(0),L,fbnB(0)]T。
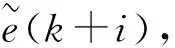
1.5 小波基函數的選擇
根據預測函數控制的方法,系統的控制精度取決于基函數的選取[17],而基函數的選取則依賴設定值以及控制對象的性質。基函數選得越少越簡單,需優化計算的加權系數也就越少,算法的快速性可以提高,但控制精度將降低。在普通的預測函數控制研究中,大多選取階躍函數、斜坡函數、指數函數以及正弦多項式函數[18]作為PFC的基函數,由于這些函數是全局函數,對參考軌跡的逼近不能隨預測時域的遞增作靈活的調整,為了解決這一不足,考慮選擇某種具有緊支撐局部特征且在布局上能靈活設置的函數作基函數。
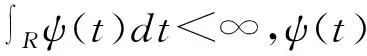
fbj(i)=B(i,j)
(13)
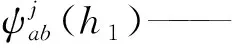
nB——基函數的個數;
nh——擬合點個數。
選擇Mexican Hat(Mexh)小波基作為陶瓷燒成窯爐溫度PFC的基函數。該小波基是Gauss函數的二階導數,在時域和頻域都具有很好的局部化特征,小波基系數衰減很快。其表達式為:
(14)
小波基函數的選取方法是:在預測時刻較小時段對參考軌跡逼近要求較高,為了滿足一定的精度要求可以設置以多個細尺度的小波基函數逼近;隨著預測時刻的增大,對參考軌跡逼近要求逐漸降低,則以少量粗尺度的小波基函數逼近,盡量減少基函數的個數。圖1和圖2為不同設置的小波基函數分布圖。
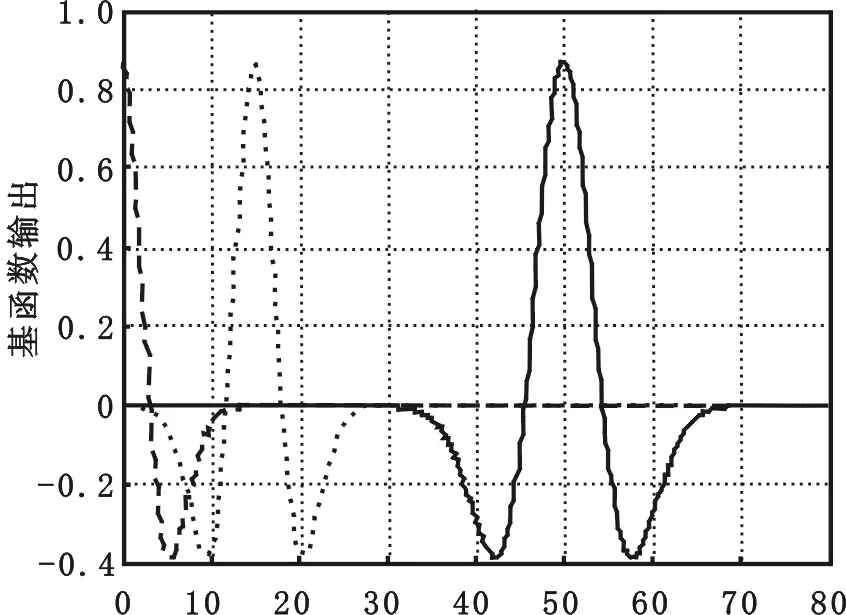
圖1 Mexican Hat(Mexh)小波基函數不均勻分布
Fig.1 Uneven distribution of Mexican Hat(Mexh )Wavelet basis function
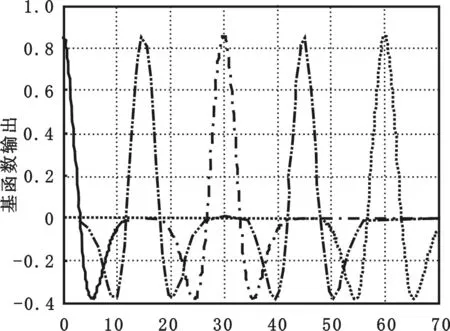
圖2 5個小波基函數均勻分布Fig.2 Even distribution of 5 Wavelet basis functions
圖1利用小波基的多尺度特性,靈活選取了3個不均勻分布小波基函數。在逼近精度較高處設置了2個細尺度的小波基函數;隨著預測時刻增大,在精度要求相對降低處設置了一個粗尺度的小波基函數,在滿足一定精度要求的同時減少基函數的個數,提高算法的快速性。圖2為在預測時域內設置的5個均勻分布小波基函數。
利用小波基函數PFC方法另外還有一個特點就是由于小波基函數是緊支局部函數,因此在式(12)表示的當前控制量u(k)時只需計算第一個小波基函數fb1(0)的權系數μ1,并不需要計算所有的權系數,因此快速性得到了進一步的提高。
2 陶瓷燒成窯爐閉環系統性能分析 [19]
假設被控對象的實際模型為:
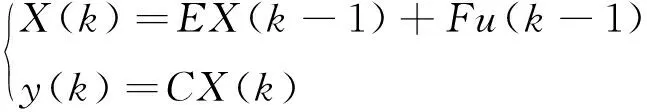
(15)
陶瓷燒成窯爐模型為常見一階系統,因此式(15)中的系數矩陣都是1×1維矩陣。當跟蹤設定值為階躍變化,由式(12)得到PFC的控制作用為:
u(k)=no(s(k)-yp(k))+nmXm(k)
(16)
考慮系統外部干擾,令:
y(k)=yp(k)+d(k)
(17)
式中:d(k)——外部擾動;
y(k)——系統的實際輸出。
由式(5)、(15)、(16)、(17)得出陶瓷燒成溫控閉環系統的輸出y(z)方程:
y(z)=yp(z)+d(z)
(18)
由上式得到傳遞函數:
(19)
(20)
式中:n0=fb1(0)yb1(h1)-1(1-αh1)
當模型匹配時,可得到
(21)
(22)
式(21)、(22)表明,預測函數控制能夠對階躍設定值實現無偏差跟蹤,理論上無穩態誤差,并且完全能夠抑制外部干擾,因此具有較強的魯棒性。
由式(18)還可以得到溫度控制閉環系統的特征方程為:
1-nm(zI-Em)-1Fm+n0C(zI-E)-1F=0
(23)
其特征根為:
(24)
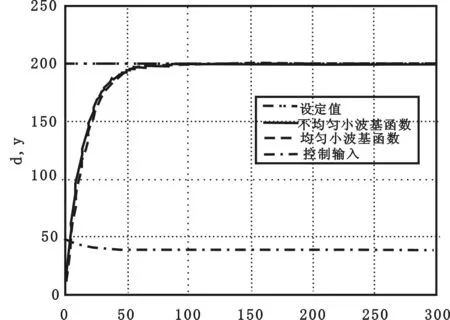
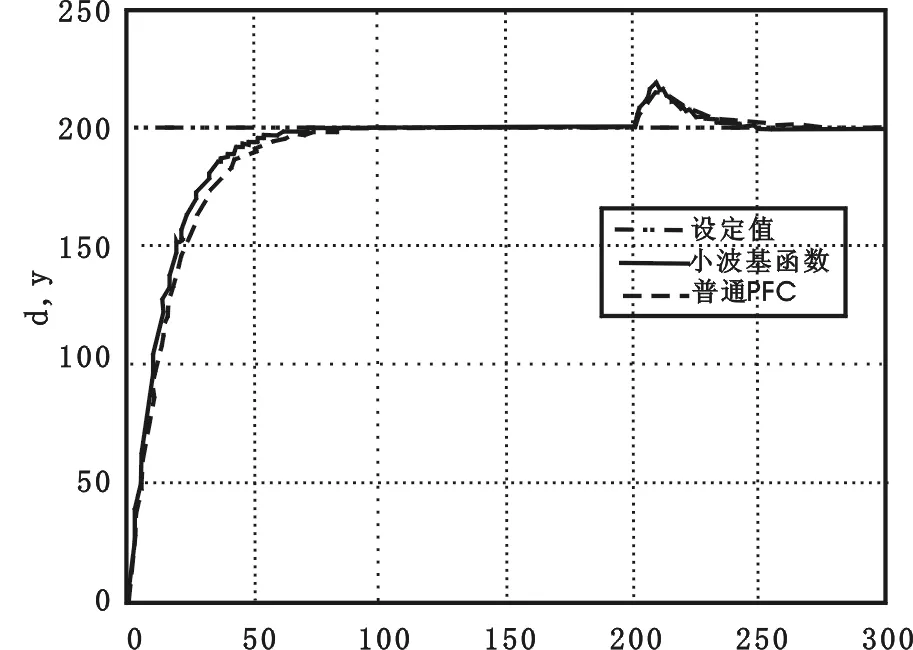
由式(7)和(10)可得出:0<α<1,h1>1。0 筆者選取純滯后一階慣性環節為陶瓷燒成溫度控制仿真對象: 其中參數取K=5,τ=10,T=20。該模型同時也作為小波基函數PFC的預測模型,并且在仿真過程中預測模型都不改變。 選取如圖1所示的3個不同預測時刻不均勻分布的小波基函數。在預測時刻較小且逼近要求較高時(p=0,15)選取細尺度(a=10)的Mexh小波;而在預測時刻較大時(p=50)選取粗尺度(a=20)的Mexh小波進行逼近。 圖3 跟蹤階躍設定值時的仿真結果比較Fig.3 Tracking the simulation results when the step setpoint 選取5個均勻小波基函數,其不同預測時刻的均勻分布如圖2所示。仿真參數不變。同時對圖1、圖2所示2種不同分布的小波基函數情況進行仿真,并進行比較,結果如圖4所示。 圖4 不同分布的小波基函數的仿真結果比較 Fig.4 Simulation results of the different distribution of the wavelet basis function 由圖4可知,不均勻分布的即具有申縮特性的小波基函數的動態特性要比均勻分布的小波基函數更好些,可見在保證一定精度的前提下,選定不均勻分布的小波基函數,減少了基函數個數,優化了待求變量的個數,提高了系統的整體控制效果。 為說明基于小波基函數PFC的抗干擾能力,在系統進入穩定時間 200 s處,加入20% 干擾信號后的響應曲線如圖5所示。仿真結果表明,加入干擾后,小波基函數PFC的溫度回到設定值的時間比普通PFC要快5~8 s。可見抑制干擾的能力優于普通PFC。 筆者利用小波基函數的緊支局部性、多尺度分析特性等特征,針對普通PFC方法中基函數的選取存在的不足,提出基于小波基函數的陶瓷燒成窯溫度預測函數控制方法。通過不同情況的仿真比較,表明小波PFC算法在顧及優化目標整體性的同時,又滿足了在不同預測時刻對參考軌跡逼近的精度要求,實現了基函數的個數和分布根據不同要求的靈活設置。該方法算法簡單,易于實現,在響應速度、控制精度、抑制外部干擾等方面比普通PFC方法都有明顯的改善,具有良好的應用前景。3 仿真比較
3.1 選取不均勻分布基函數
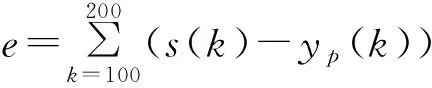
3.2 選取均勻分布基函數
3.3 受干擾情況
4 結語

