Cl0，2k＋1的張量積分解式與矩陣表示

宋元鳳，李武明

（1.吉林大學 數學學院，長春130012；2.通化師范學院 數學學院，吉林 通化134002）

Clifford代數在高維幾何、理論物理、編碼理論、機器人科學和地理科學等領域應用廣泛［1－2］.設Clp，q為?p，q上的實 Clifford代數，Lee等［3－4］給出了實 Clifford代數Cl0，3的一種矩陣表示；曹文勝［5］給出了Cl0，3的另外兩種矩陣表示，并探討了其運算性質；文獻［6］給出了實Clifford代數Clp，q的張量積表達式與矩陣表示，其中把實Clifford代數Clp，q的中心作為張量積分解式的一個因子.本文把文獻［6］的結果進一步細化，給出了實Clifford代數Cl0，2k＋1的張量積分解式及矩陣表示.當Cl0，2k＋1的中心同構于?時，得到了“Cl0，2k＋1同構于Cl1，1的k次張量冪和Cl0，1的張量積”的結論，并利用該結果得到Cl0，2k＋1的矩陣表示，由于此時Cl0，2k＋1為單代數［7］，所以在同構意義下Cl0，2k＋1的矩陣表示是唯一的.當Cl0，2k＋1的中心同構于?與?的直和時，得到了Cl0，2k＋1的張量積分解與矩陣表示，但此時矩陣表示不一定是唯一的.結合上述兩種情況，得到了本文的主要結果：

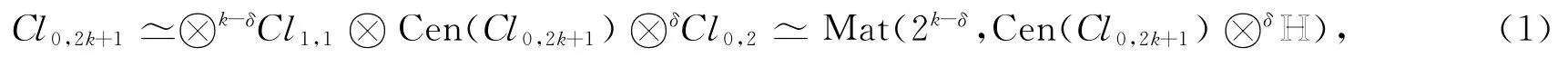
其中：k為非負整數；2k＋1≡αmod 8；δ＝［1－｛α／3｝］.特別地，當2k＋1＝3時，可得一種與文獻［3－5］形式不同的矩陣表示.

本文HH 表示四元數，?kCl1，1表示Cl1，1的k次張量冪，Cen（Clp，q）表示實 Clifford代數Clp，q的中心，e12…s為Cl0，2k＋1的s次單位向量，Mat（2，?）表示2階實矩陣代數，｛a｝表示實數a的小數部分，［a］表示實數a的整數部分，其他符號參見文獻［8－9］.

1 Cl0，2k＋1的張量積分解

設｛e1，e2，…，ep＋q｝是?p，q的一組標準正交基，Clp，q上的Clifford乘積定義為

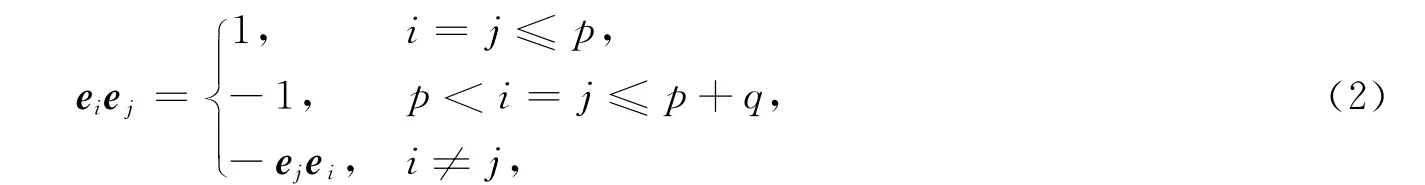
因此實 Clifford代數Clp，q是2p＋q維結合代數［8］.

本文從中心同構于?和?與?直和兩種情況探討Cl0，2k＋1的張量積分解，首先給出中心同構于?和?與?直和的充要條件.

引理1 設k是非負整數，則如下3個結論等價：

1）Cen（Cl0，2k＋1）同構于二維實代數?；

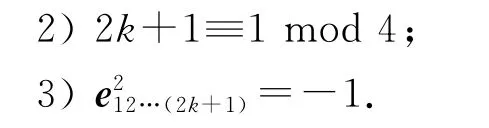
證明：設e12…（2k＋1）為Cl0，2k＋1的2k＋1次單位向量，則

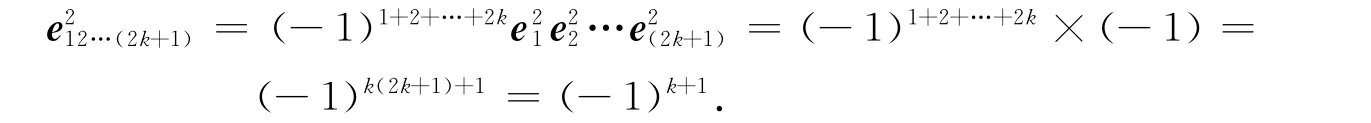
根據文獻［6］經簡單計算即可得結論.

引理2 設k是非負整數，則如下3個結論等價：

1）Cen（Cl0，2k＋1）同構于二維實代數?⊕?；

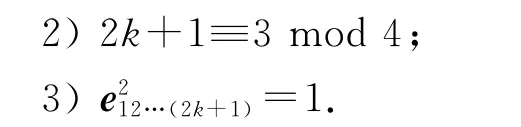
證明類似于引理1.

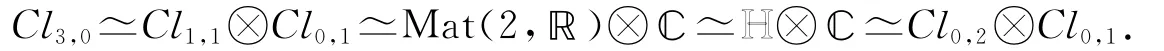
事實上，Cl3，0可視為由〈e1，e2〉和〈e123〉的乘積生成，而

經簡單的張量積驗證易知

Cl3，0也可視為由〈e12，e13〉和〈e123〉的乘積生成，而

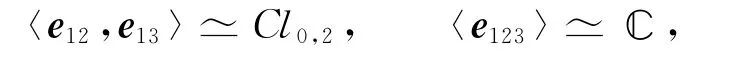
經簡單的張量積驗證易知

注1 引理3的內容可參見文獻［8］中第四章與第十七章，為考察Cl3，0的結構本文給出了Cl3，0的另一種證明.

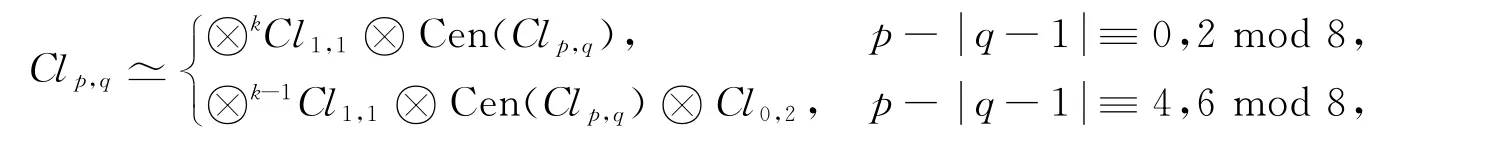
所以當2k＋1≡1mod 8時，式（3）成立.當2k＋1≡5mod 8時，由引理3有

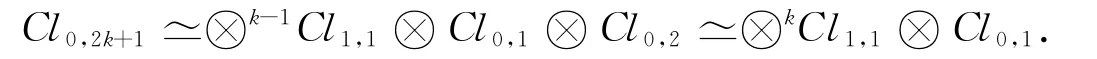
由文獻［6］經簡單計算可得如下引理.

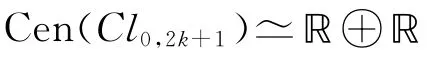
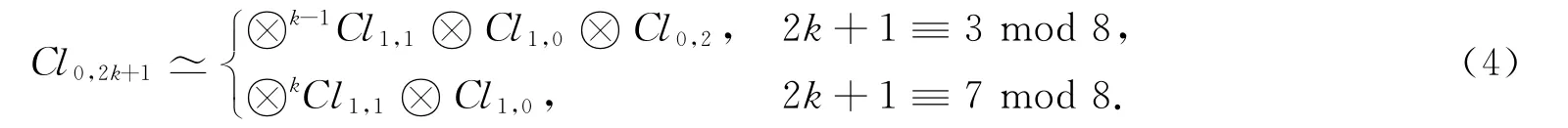
結合引理4和引理5可給出Cl0，2k＋1的張量積分解式：

定理1 設k是非負整數，則

其中：2k＋1≡αmod 8；δ＝［1－｛α／3｝］.

2 Cl0，2k＋1的矩陣表示

定義1［10］設A 是有限維F－代數，V 是有限維F－向量空間.如果存在 F－代數同態ρ：A→EndF（V），則稱（V，ρ）是A的一個F－表示.

定義2［10］如果存在F－線性同構f：M→N，使得?a∈A，fρ（a）＝η（a）f，則稱A的兩個F－表示（M，ρ）和（N，η）等價.

設Fm表示域F上的m 階全矩陣代數.對于A＝（aij）∈Fm，B＝（bij）∈Fn，記

或

設

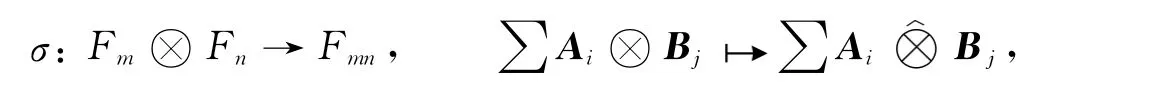
引理6 當 Cen（Cl0，2k＋1）??時，

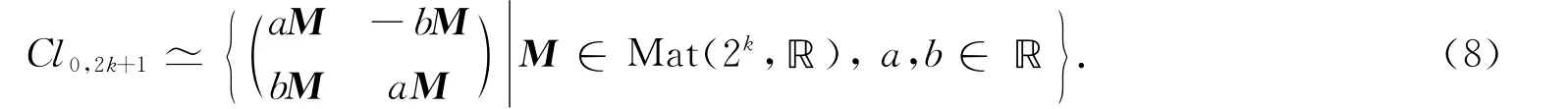
證明：因為

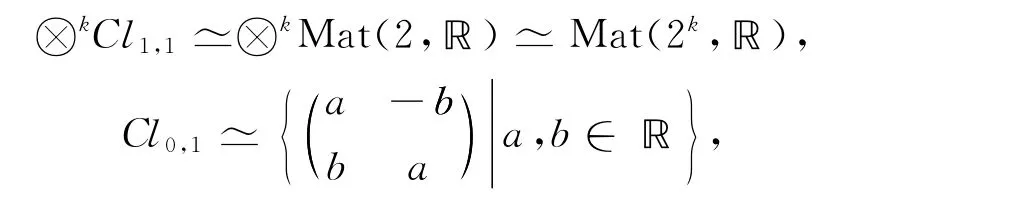
所以當 Cen（Cl0，2k＋1）??時，

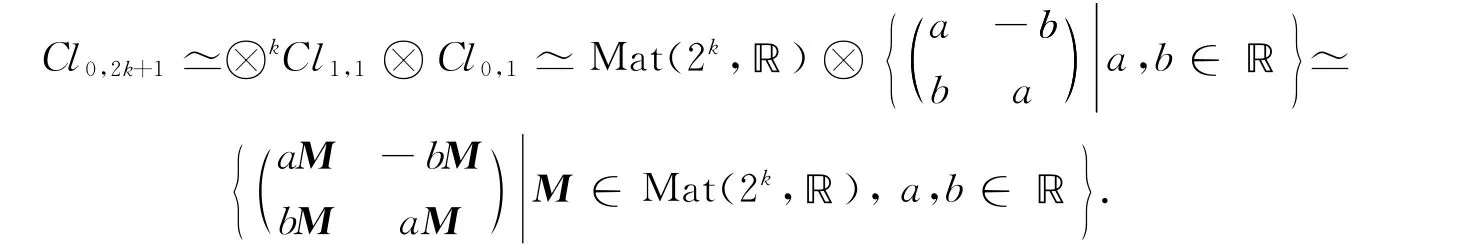
引理7 設 Cen（Cl0，2k＋1）??⊕?.

1）如果2k＋1≡7mod 8，則

2）如果2k＋1≡3mod 8，則

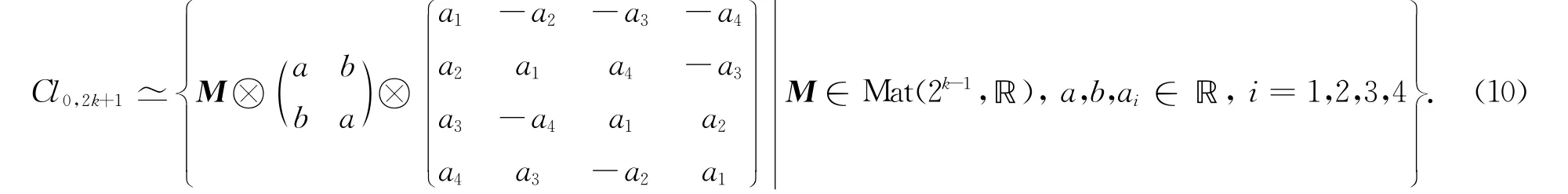
證明：1）如果2k＋1≡7mod 8，則有式（3）.因為

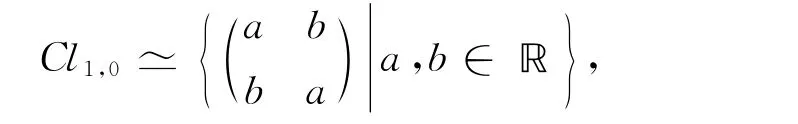
所以

2）如果2k＋1≡3mod 8，則

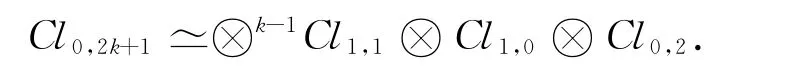
因為

所以

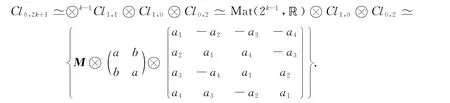
特別地，當2k＋1＝3時，

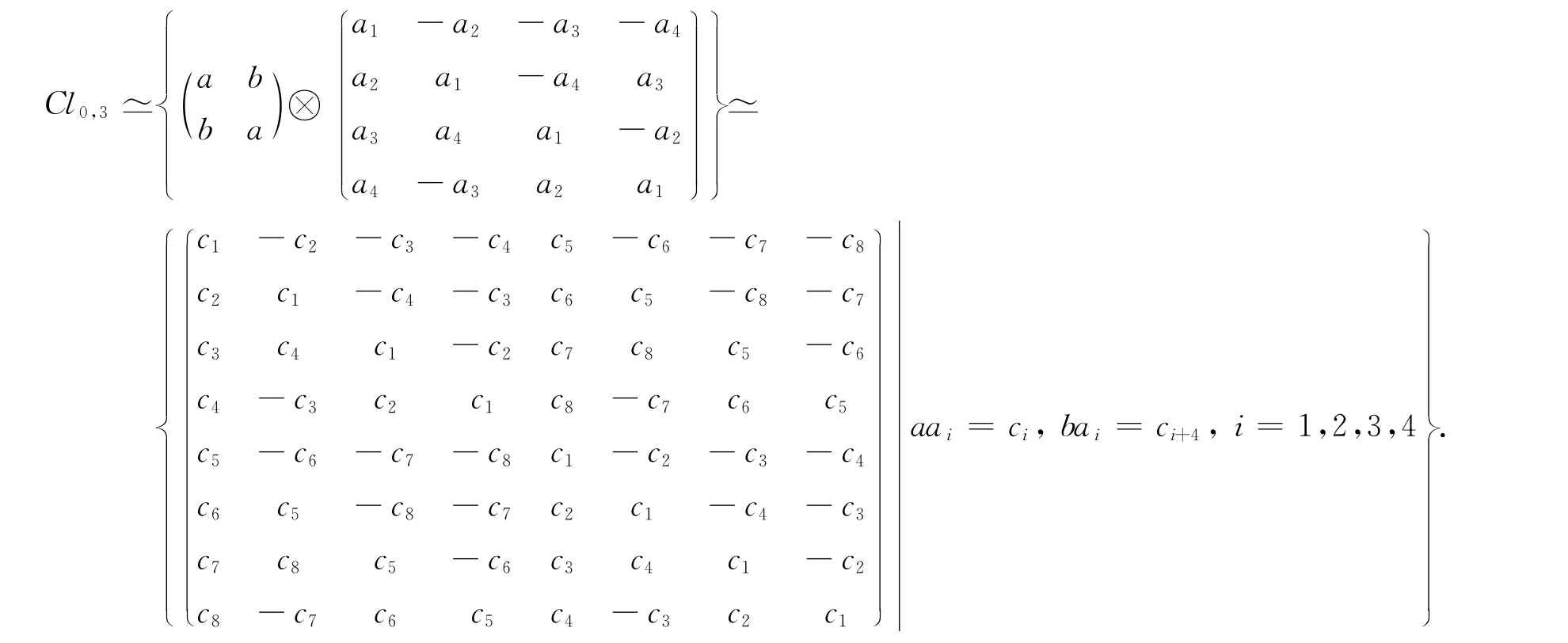
又

結合引理6和引理7可得：

定理2 設k是非負整數，

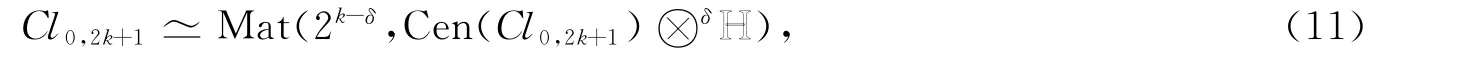
其中：2k＋1≡αmod 8；δ＝［1－｛α／3｝］.

［1］Baylis W E.Clifford（Geometric）Algebras with Applications to Physics，Mathematics and Engineering［M］.Boston：Birkh?user，1996.

［2］Corrochano E B，Sobczyk G.Geometric Algebrawith Applications in Science and Engeneering［M］.Boston：Birkh?user，2001.

［3］Lee D H，Song Y K.The Matrix Representation of Clifford Algebra［J］.J Chungcheong Math Soc，2010，23（2）：363－368.

［4］Lee D H，Song Y K.Applications of Matrix Algebrato Clifford Groups［J］.Adv Appl Clifford Algebra，2012，22（2）：391－398.

［5］CAO Wen－sheng.Similarity and Consimilarity of Elements in 4－Dimensional Clifford Algebra ［J］.Acta MathematicaScientia，2010，30A（2）：531－541.（曹文勝.四維 Clifford代數的相似與合相似 ［J］.數學物理學報，2010，30A（2）：531－541.）

［6］SONG Yuan－feng，DU Xian－kun，LI Wu－ming.Real Clifford Algebras as Tensor Products over Centers［J］.Adv Appl Clifford Algebra，2013，23（3）：607－613.

［7］劉紹學，郭晉云，朱彬，等.環與代數 ［M］.2版.北京：科學出版社，2009.

［8］Lounesto P.Clifford Algebras and Spinors［M］.2nd ed.Cambridge：Cambridge University Press，2001.

［9］Gallier J.Clifford Algebras，Clifford Groups and aGeneralization of the Quaternions：The Pin and Spin Groups［D／OL］.2013－11－12.http：／／arxiv.org／pdf／0805.311v2.pdf.

［10］馮克勤，章璞，李尚志，等.群與代數表示引論 ［M］.2版.合肥：中國科學技術大學出版社，2003.