大型船舶艉管軸承結構參數優化設計

何江華，潘偉晶，習 猛，劉 濤

（滬東中華造船（集團）有限公司，上海 200129）

0 引 言

推進軸系在船舶動力裝置中起著重要的作用。在軸系的運轉過程中，軸承與軸頸之間產生油膜，船舶正常航行時，軸系平穩運轉，軸頸和各軸承之間處于良好的潤滑狀態，潤滑油膜均勻分布。但由于船舶主機輸入功率不穩定、船體振動和在風浪中的變形、螺旋槳不均勻伴流場、船舶大轉彎操縱等多種因素的交互作用，造成船舶軸系運轉不穩定，軸心位置不斷變化。尤其對艉管后軸承，由于其特殊位置，需要承受較大的螺旋槳懸臂作用、慣性作用及水動力作用，常常處于非常惡劣的潤滑狀態，惡劣工況下甚至會造成艉管軸承副的干摩擦。

在船舶艉管軸承的設計中，結構參數根據實際經驗選定，油潤滑艉管軸承長度一般為艉管軸承直徑的2～2.5倍，溝槽位置一般為90°、180°布置。軸承的徑向間隙對整個軸承的承載能力也有很大的影響，在以前的艉管軸承設計中，軸承間隙由經驗公式計算，此間隙并不能保證軸承潤滑特性最佳，從而影響軸承的設計質量。

國內外一些學者研究了溝槽對滑動軸承性能的影響。溝槽作為滑動軸承結構的一個重要部分，其作用在于輸送和分布潤滑油，其位置、形狀和結構參數對軸承的性能影響很大。郭力，汝元功分析了具有部分周向油溝的液體動壓滑動軸承動特性，和部分周向溝槽的油壓對該軸承動特性的影響。支偉華提出在軸承上加工簡單的溝槽可以改進滑動軸承的性能，提出了油溝的最佳位置[1]。秦路，等研究了對于溝槽開設位置、溝槽尺寸大小對滑動軸承性能的具體影響過程[2]。目前一般認為，油孔應設置在油膜壓力最小的地方；溝槽應開在軸承不受力或油膜壓力較小的區域，要求既便于供油又不降低軸承的承載能力[3,4]。艉管軸承潤滑性能參數的計算是對其進行優化設計的基礎。

1 流體動力潤滑理論

1.1 流體動力潤滑理論

由于徑向滑動軸承中軸與軸承之間存在偏心距，因而在旋轉的動態過程中，軸承間隙由大變小又由小變大。當間隙由大到小的過程中形成楔形，在這一區域油膜壓力急劇增大，油膜壓力分布曲線見圖1，就是承載載荷的主要條件[5,6]。

1.1.1 分析假設

為模型數值計算的方便, 作如下基本假設：1) 壓力沿油膜厚度方向不變；2) 由于油的密度、粘度隨壓力、溫度的變化很小，而認為它們在軸運轉的過程中恒定不變；3)軸承在工作時的狀態為準穩態，即密度、膜厚等參數不隨時間改變；4) 由于艉軸采用斜鏜孔工藝，不考慮艉軸傾斜對軸承承載能力的影響。

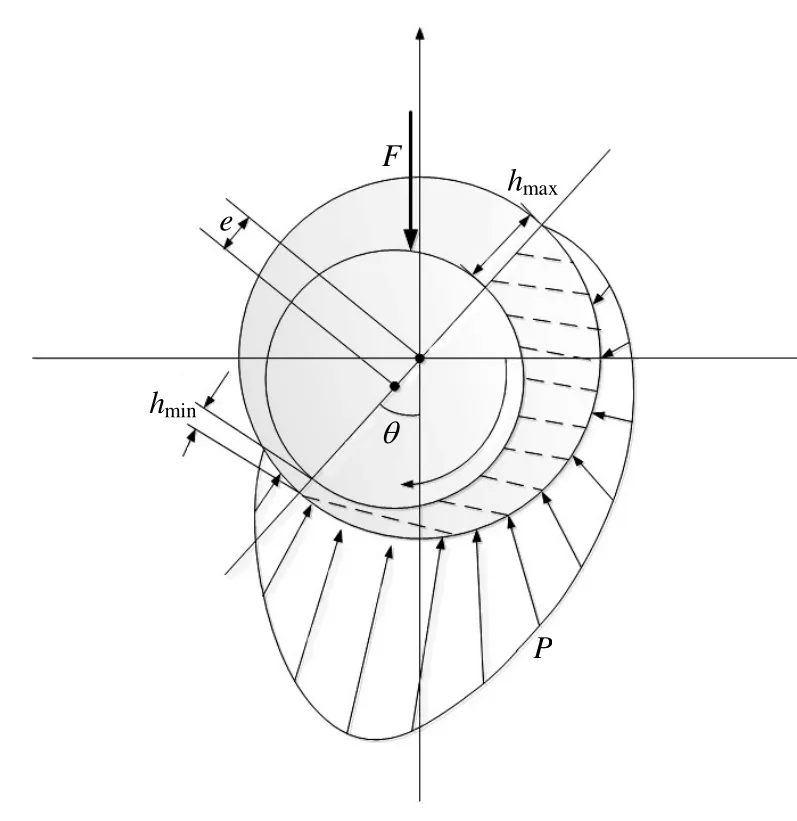
圖1 油膜徑向壓力分布

1.1.2 雷諾方程

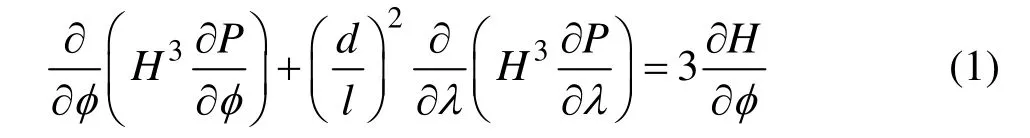
式中：P=p/p0——無量綱油膜壓力；p——實際油膜壓力，p0=2Ωμd2/c2；Ω——軸頸的轉速；c——半徑間隙比；μ——潤滑油的動力粘度；d——軸頸半徑；l——軸承的寬度； H =1 + εcos φ，ε——偏心率；λ=z/ l——軸承的無量綱軸向坐標，z——軸承的軸向坐標；φ=r/x——軸承的無量綱周向坐標，r——軸承半徑；x——軸承周向坐標。

1.1.3 邊界條件

在徑向，艉管軸承潤滑的邊界條件由兩部分組成：一種是軸承結構邊界條件，在油槽位置處壓力為零。另一部分是油膜終止邊界條件，采用Reynolds邊界條件，即在油膜破裂處無量綱油膜壓力為零，壓力梯度也為零。在軸向由于艉管軸承完全浸沒在潤滑油中，取兩端油膜壓力為供油壓力，即其無量綱油膜壓力為零。

式中：θs——油壓起始位置；θc——油壓產生空穴的位置；θi——附加的進油口位置[7]。

1.1.4 艉管軸承載荷分析

船舶在試航期間，當主機的功率調整到最大持續功率（Maximum Continuous Ratings，MCR；約27300kW）準備耐久實驗時，艉管后軸承的尾端兩個溫度傳感器顯示溫度開始升高，從約32℃開始，緩緩持續上升到41℃以上，甚至在一次操舵后其中一只傳感器溫度突然上升到70℃以上。在航行時只要舵角轉動較快就會引發艉軸承溫度持續升高，只有停止轉動舵角并降低航速才使艉軸承溫度趨于正常，且在高航速的情況下也會出現艉軸溫度突然升高的情況[8]。

圖2 艉管軸承磨損

在進塢檢查時，觀察到艉管后軸承末端約135°～165°處有軸承與艉軸摩擦的痕跡（見圖2），這表明高溫是由艉軸承與艉軸摩擦引起的。艉軸承與艉軸之間的油膜潤滑已遭到破壞，在約135°～165°方向，最小油膜厚度已經超過了允許的極限值，導致艉軸承與艉軸之間的潤滑狀態已經由油膜潤滑轉為油膜與干摩擦的混合狀態，或者是直接的干摩擦狀態。經計算分析，確定外載荷的方向為150°，根據艉管軸承的其他設計參數，獲得軸承的承載能力。數值分析時的起始角度，涉及到油膜厚度的計算，起始角為330°。

1.2 Reynold方程數值解

通常采用差分法和有限元法求解雷諾方程。這里選用差分法求解滑動軸承的壓力分布，對軸瓦的油膜區域劃分為網格（見圖3）。用各個節點上的壓力值構成各階差商，近似取代雷諾方程中的導數，將方程化為一組代數方程，由此解出各節點上的壓力值。

對(i, j)點上的一階導數用，?P/?φ,?P/?λ，使用其相鄰節點上的P值構成的中間差商的近似表達，為提高計算精度以半步長為計算單位，采用半步長插入點上的壓力和厚度值計算，構成一組(m-1)(n-1)個內節點Pi,j值的線性非齊次代數方程，從而解出各個內節點 Pi,j。

采用式(6)所示的相對精度收斂準則來判斷迭代的結果是否已達到所要求的精度，從而決定是否可以終止迭代。

采用matlab編程計算，計算流程見圖4。

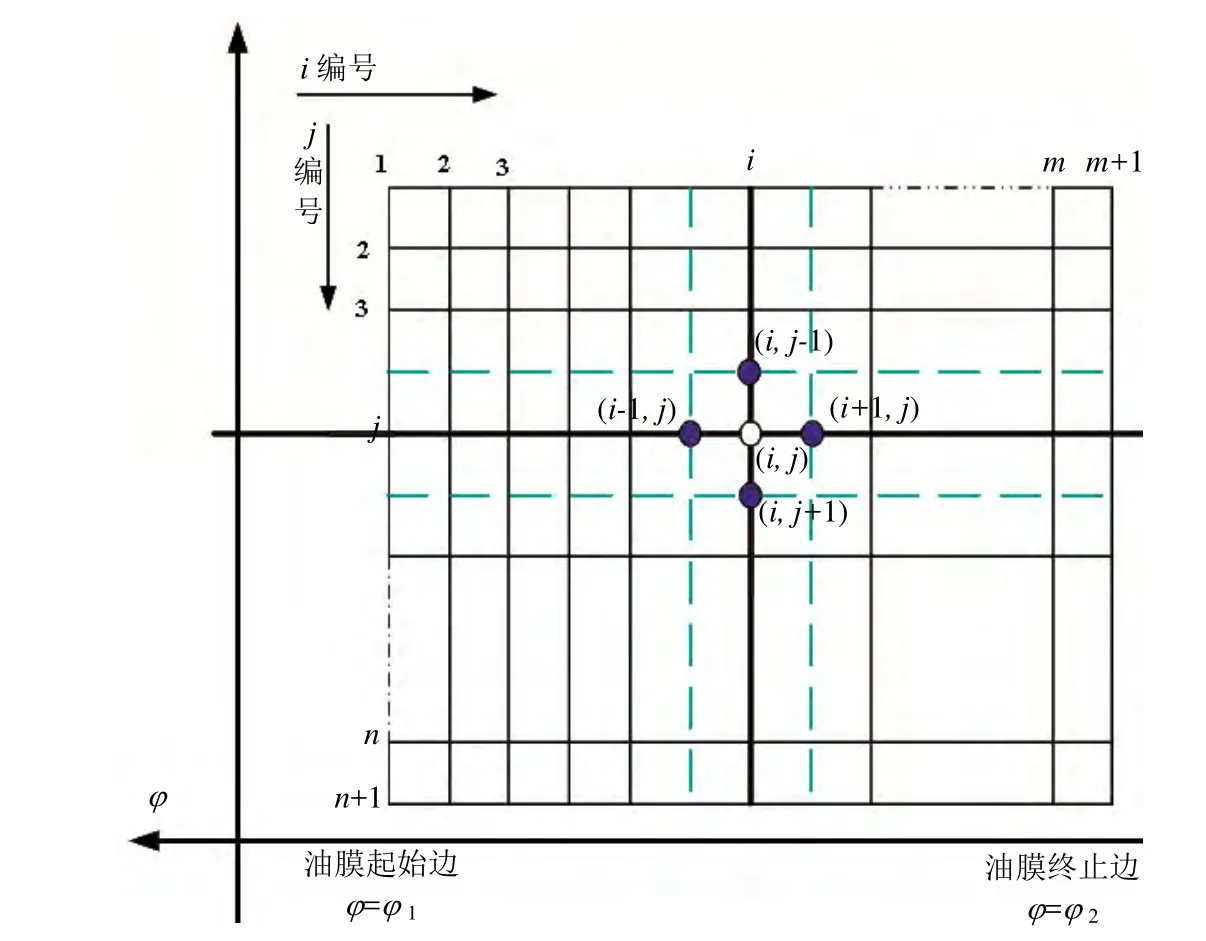
圖3 網格

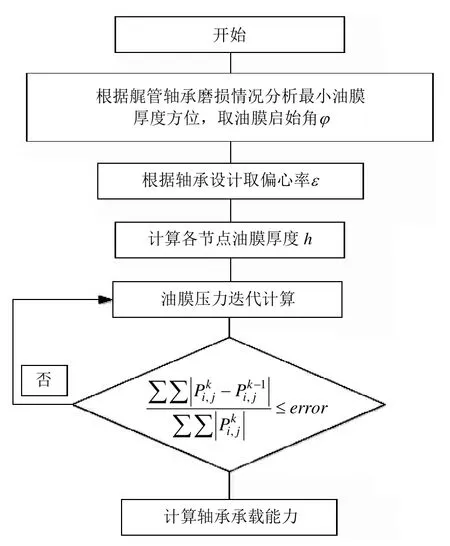
圖4 計算流程

2 艉管軸承流體動力潤滑分析

對該軸承的優化設計如下：修改前，軸承溝槽位置90°，180°方向，溝槽寬度40mm，艉管軸承長度1560mm，直徑775mm，軸承間隙1.4mm。修改后軸承溝槽位置60°，300°方向，溝槽寬度40mm，艉管軸承長度1560mm，直徑775mm，軸承間隙1.6mm（見圖5、6）。對于已經設計好的艉管軸承，因最小油膜厚度已經確定，加大軸承的間隙比。當允許的最小油膜厚度為0.1mm時，ε=0.9286，ε表示初始偏心率，ε1=0.9375，ε1表示改進后的偏心率。

通過數值計算，可以得到改進前后的艉管軸承油膜壓力分布圖（見圖7、8）。

2.1 不同溝槽位置時軸承承載能力分析

90°，180°溝槽設計時承載能力：p=9.06×105N；60°，300°溝槽設計時承載能力：p=9.90×105N；承載能力提高量：9.27%。

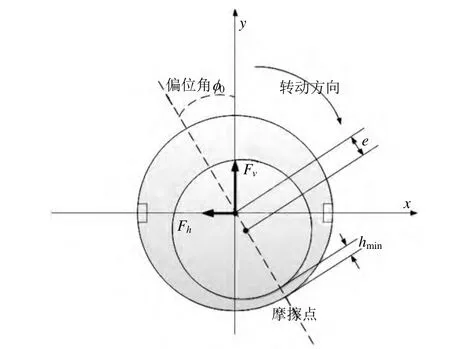
圖5 改進前雙溝槽艉管軸承

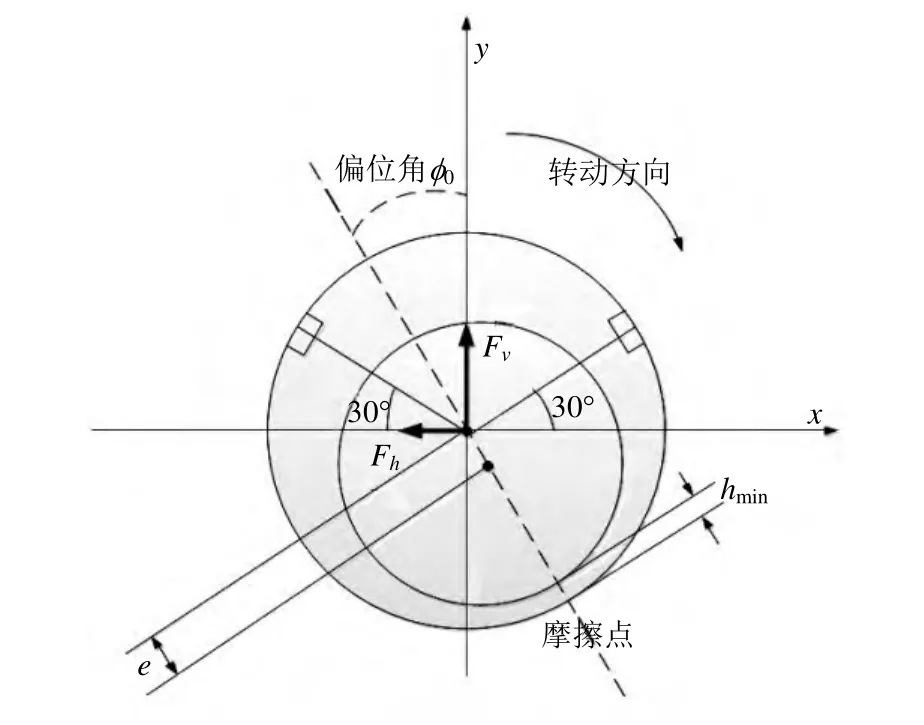
圖6 改進后雙溝槽艉管軸承

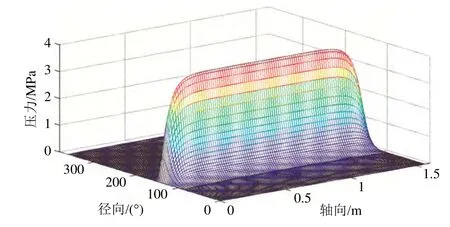
圖7 改進前90°，270°溝槽，1.44mm間隙時壓力分布

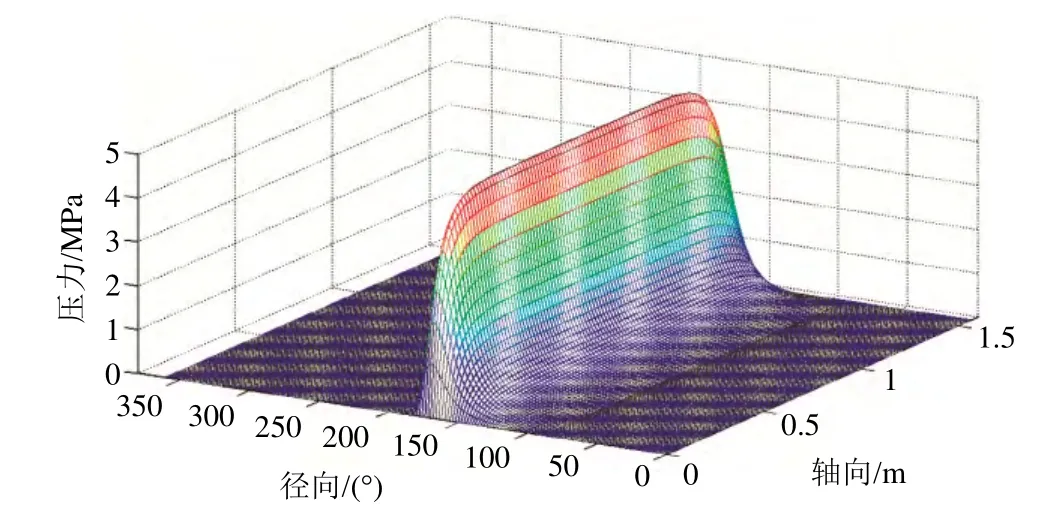
圖8 改進后60°，300°溝槽，1.44mm間隙時壓力分布

2.2 改進間隙設計后軸承承載能力分析

90°，180°溝槽設計時：p=1.05×106N；承載能力提高量：15.89%。

2.3 同時改進溝槽和間隙后

60°，300°溝槽，相對偏心率：0.9375；軸承承載能力：p=1.14×106N；承載能力提高量：25.83%。

通過上述的定量分析表明，改進后，當最小油膜在135°方向時，艉管軸承的承載能力提高了25.83%。通過優化設計，船舶重新試航，在各種工況下，未出現艉管軸承高溫報警。

3 結 語

基于流體動力潤滑理論對某大型船舶艉管軸承進行優化設計，分別將艉管軸承溝槽位置由原來的90°，180°方向改為60°，300°方向，軸承間隙由原來的1.4mm改為1.6mm，通過數值計算分析表明，改進設計后的艉管軸承的承載能力提高了25.46%。通過優化艉管軸承設計，該船在再次試航和船舶營運期間，未再出現艉管軸承高溫報警。

[1] 王賢烽. 船舶系艉管軸承的優化設計及試驗研究[J].中國造船，1994, (1): 74-86.

[2] 秦 路，張志明，周 瓊，安 琦. 油溝結構參數對滑動軸承性能的影響[J]. 華東理工大學學報（自然科學版），2010,36 (5): 125-131.

[3] 郭 力，汝元功.具有部分周向油槽液體動壓滑動軸承的動特性[J].東南大學學報，1991, 21(5): 53-59.

[4] 支偉華，吳承基. 改進滑動軸承的性能：在軸承上加工簡單的油槽可以改進性能[J].杭州機械，1990, (3): 41-43.

[5] 張直明. 滑動軸承的流體動力潤滑理論[M]. 北京：高等教育出版社，1986.

[6] 王良武，周瑞平. 船舶推進軸系艉管軸承潤滑性能研究與分析[C]. 第四屆全國船舶與海洋工程學術會議論文，2008:342-347.

[7] J.K. Wanga, M.M. Khonsari, Effects of Oil Inlet Pressure and Inlet Position of Axially Grooved Infinitely Long Journal Bearings. Part I: Analytical Solutions and Static Performance. Tribology International[J]. 2008, 41:119–131.

[8] 何江華，潘偉昌，羅 樂. 軸系動態校中技術在大型船舶上的應用研究[J].船舶與海洋工程，2014, (1): 65-70.