面向應急任務衛星魯棒性規劃模型及算法

鄧潤，唐宏，單越，牛曉楠，劉穎慧

（北京師范大學 地表過程與資源生態國家重點實驗室，北京 100875）

1 引 言

成像衛星具有一次成像范圍大、成像成本低等特點，已廣泛應用于國防、環保、農業、氣象、災害應急等領域。然而，成像衛星研制、發射和維護成本高，盡管隨著衛星應用技術的發展，越來越多的成像衛星升入太空，但相對于人類日益增長的成像需求，衛星資源仍然異常寶貴。為了最優化地利用成像衛星資源，衛星任務規劃尤為重要。成像衛星受到軌道限制僅在特定的時間窗口內與地面目標可見，衛星任務規劃［1］即綜合考慮衛星成像能力及任務需求等約束，以安排最大任務收益為優化目標，確定要執行的任務及執行這些任務的時間窗起止時間。現有研究［2－6］大多集中在衛星靜態任務規劃，當新的應急成像任務到來時，采用完全重規劃算法對原問題重新建模求解。產生的新任務規劃方案與初始方案相差較大，導致衛星重調度難度大。

針對衛星動態任務規劃，Perberton等［7］總結了4種引起衛星任務規劃方案調整的因素：任務觀測機會變化、資源變化、新任務插入、衛星任務規劃問題參數變化，但并未提出具體的問題模型及求解算法。Verfaillie［8］和劉洋［9］提出基于動態約束滿足問題的衛星動態任務規劃模型及求解算法，但并未考慮初始方案的可調整性。王軍民［10］將衛星任務動態規劃問題分為魯棒性初始方案生成及調整兩個階段，在初始方案生成階段，引入基于鄰域的魯棒性指標，得到更易于調整的初始方案，當新任務與初始方案中的任務沖突時，能使初始方案中的任務安排到其他位置而不被刪除，但基于鄰域的魯棒性指標不能衡量初始方案接受新任務直接插入而不影響已安排任務執行的能力。

本文在衛星魯棒性任務規劃模型目標函數中引入總時間重疊度及總任務執行時長兩項魯棒性指標，通過仿真模擬實驗結果分析可知，在任務收益和相差不大的情況下，采用本文方法能得到總時間重疊度更小，總任務執行時長更短的衛星魯棒性任務規劃方案。

2 衛星魯棒性任務規劃模型

2.1 魯棒性指標

對于給定的規劃方案，在面臨擾動時，應用某種特定的動態調整方法既能保持良好的規劃方案收益，又能保持新老規劃方案的差異盡可能小，則稱之為魯棒性規劃方案［10］。

本文提出兩項魯棒性指標：①總任務執行時長，衡量規劃方案接受新任務直接插入而不影響已安排任務執行的能力；②總時間重疊度，衡量規劃方案中已安排任務與新任務沖突時，能被重新安排在其他時間窗口執行的能力。

定義1總任務執行時長：各衛星安排執行任務時間之和。

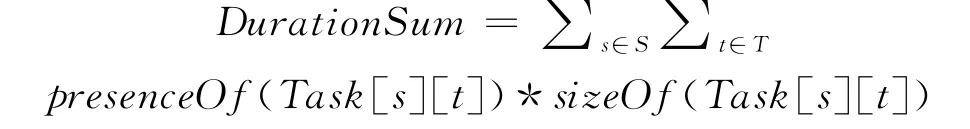
（上式中涉及的變量、函數意義見2.2節模型中涉及的變量、參數及函數部分）

總任務執行時長算例：

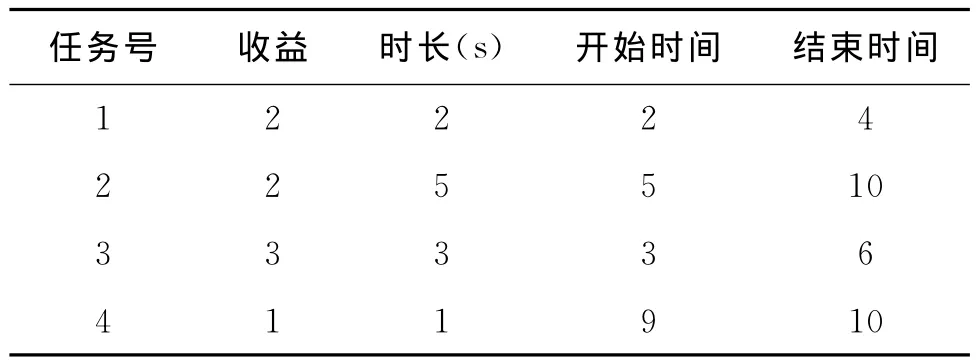
表1 各任務收益及衛星a與任務可見時間窗口

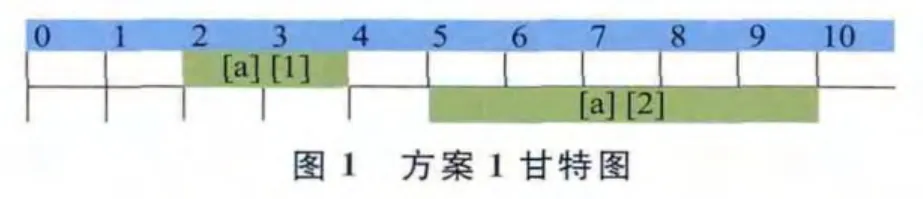
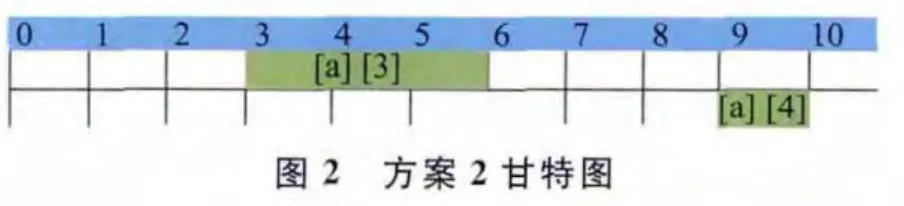
表1列舉出衛星a與4個待執行任務間的可見時間窗口、任務收益及衛星完成各拍攝任務需要的時長。其中，任務收益根據各任務的重要性設定，任務越重要，衛星執行任務獲得的收益越高，衛星任務規劃方案的任務收益和即方案中所有已安排執行任務的收益和。由圖1可知，方案1中衛星a最終執行任務1和任務2；圖2顯示方案2中衛星a執行任務3和任務4，兩方案任務的收益和均為4，方案1總任務執行時長＝2＋5＝7，方案2總任務執行時長＝3＋1＝4。在規劃時段0～10內，顯然方案2的空余時間窗口更多，接受新任務直接插入能力更強。此外方案2總執行時長短，衛星能量消耗更低，因此任務收益和指標相同的情況下，總任務執行時長越短的方案性能越好。

定義2 總時間重疊度：各衛星執行任務時間窗口與衛星其余可見時間窗口的時間重疊度乘以任務權重的和。

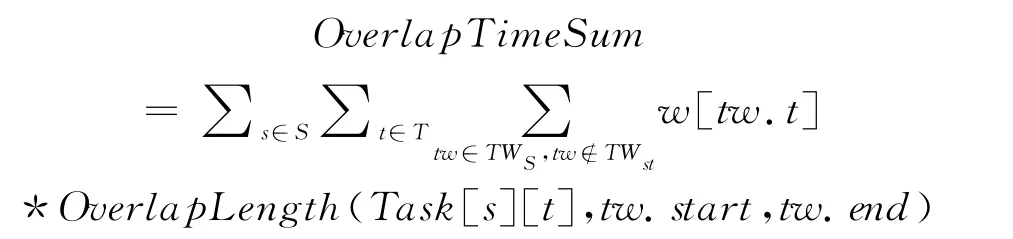
（上式中涉及的變量、函數意義見2.2節模型中涉及的變量、參數及函數部分）

總時間重疊度算例：

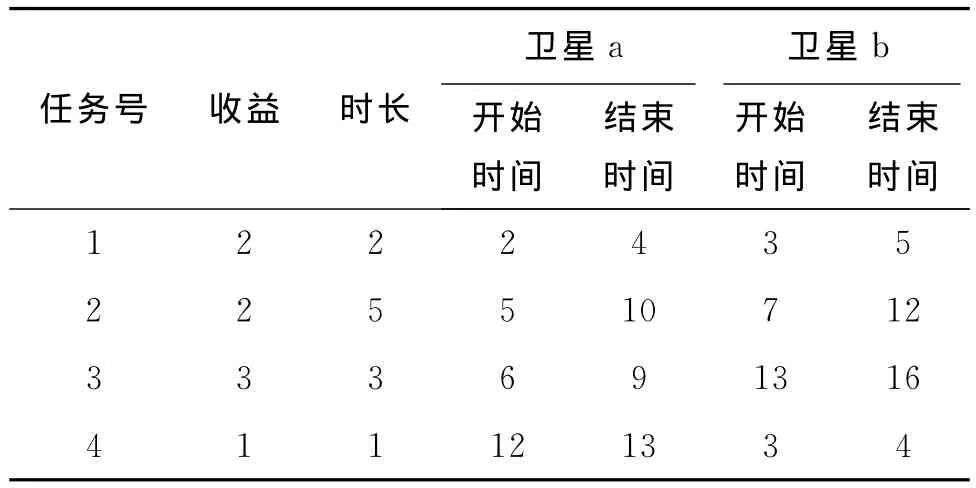
表2 各任務收益及其與衛星a，b可見時間窗口

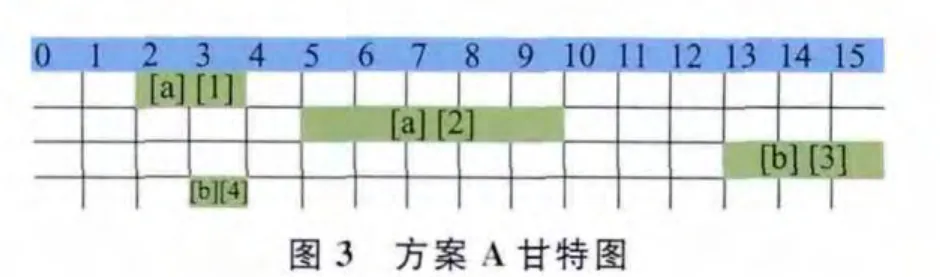
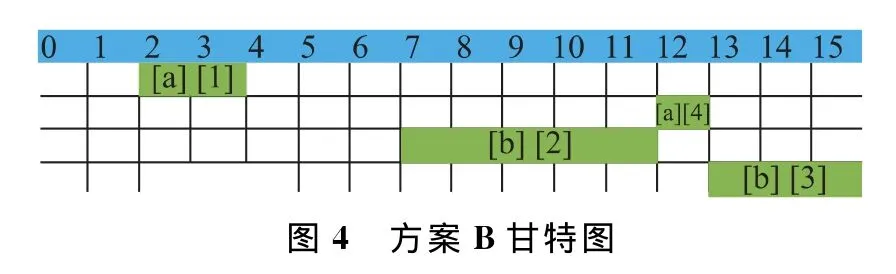
由圖3、圖4可知，方案A、方案B的任務收益和指標均為11，方案A總時間重疊度＝3×3＋2×1＝11，方案B總時間重疊度為0，當新應急任務到來要占用任務1或者任務3的時間窗口時，方案A總時間重疊度較高，能重新安排任務1的潛在時間窗口［3 5］與任務4重疊，能重新安排任務3的潛在時間窗口［3 6］與任務2重疊，導致任務1、任務3都無法重新安排。而方案B總時間重疊度為0，能重新安排任務的潛在時間窗口都與方案中的其他任務沒有重疊，故當新應急任務插入引起沖突時，沖突位置的任務能重新安排到其他時間窗口執行，無需刪除，因此任務收益和指標相同的情況下，總時間重疊度小的任務規劃方案更優。

2.2 面向應急任務衛星魯棒性任務規劃模型

本文引入總任務執行時長、總時間重疊度兩項魯棒性指標，建立的衛星魯棒性任務規劃約束滿足問題模型如下：

以上各式表達的含義如下：

式（1）表示任務收益和最大；

式（2）表示總時間重疊度最小；

式（3）表示總任務執行時長最短；

式（4）表示每個任務最多被執行一次；

式（5）表示每顆衛星的執行任務序列中不存在重疊的時間段，即各衛星同一時間僅執行一個任務；

式（6）表示衛星執行任務必須在兩者可見時間窗口內進行；

式（7）表示任意單圈時間段內，衛星執行任務的總時長必須小于衛星單圈最長執行任務時長。

模型中涉及的變量、參數及函數：

（1）決策變量：

Task［s］［t］：時間區間變量（interval），表示衛星s執行任務t的時間窗口；

Satellites：將衛星s執行任務的時間窗按時間順序排序得到的任務序列，表示衛星s的執行任務序列。

（2）其他參數：

ω（t）：成像任務t的收益；

tw：衛星與任務間可見時間窗口四元組＜s，t，start，end＞，對應信息＜衛星，任務，開始時間，結束時間＞；

TW：可見時間窗口集合；

TWs：衛星s的可見時間窗口集合；

TWst：衛星s對任務t的可見時間窗口集合；

S：參與成像衛星集合；

T：成像任務集合；

maxdurations：衛星s單圈最長執行任務時長；

orbittimes：衛星s單軌運行時間。

（3）函數：

presenceOf（interval a）：若a在調度方案中出現則返回1，否則返回0；

sizeOf（interval a）：返回a的大小；

overlapLength（interval a，int b，int c）：返回a與［b c］間重疊時間長度；

startOf（interval a）：返回時間區間變量的開始時間。

3 衛星魯棒性任務規劃算法

3.1 基于NSGA－П衛星魯棒性任務規劃算法

衛星魯棒性任務規劃問題是典型的多目標優化問題，目前求解多目標優化問題大多采用多目標進化算法。針對上述衛星魯棒性任務規劃模型，本文基于經典多目標優化算法 NSGA－П［11－12］框架（圖5）設計了衛星魯棒性任務規劃算法。

算法流程如下：

（1）設計解的遺傳編碼，設置種群大小M，最大迭代次數T，當前迭代次數t＝0，并初始化種群Pt；

（2）對種群Pt進行選擇，交叉，變異遺傳操作，產生新種群Qt；

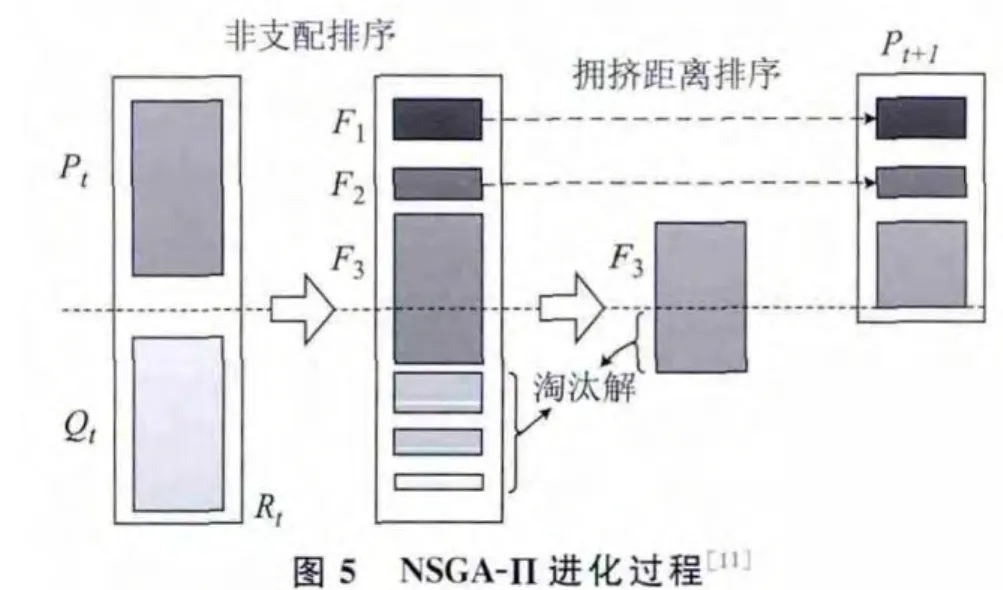
（3）對新種群Rt＝（Pt∪Qt）進行非支配排序（Non－dominated sorting）得到Rt的非支配前沿F＝（F1，F2，…）；

（4）令Pt＋1＝?，i＝1，Pt＋1＝Pt＋1∪Fi；

（5）i＝i＋1，若｜Pt＋1｜＋｜Fi｜＜M，轉（4），若｜Pt＋1｜＋｜Fi｜＝M，轉（7）；

（6）計算Fi中個體的擁擠距離，并按擁擠距離選出最好的｜M－｜Pt＋1｜｜個體，Pt＋1＝Pt＋1∪Fi［1∶｜M－｜Pt＋1｜｜］；

（7）t＝t＋1，若t＋1＜T且Pt＋1∩Pt≠Pt，重復（2）；

（8）輸出Pt中的非支配pareto解并解碼。

3.2 遺傳算子設計

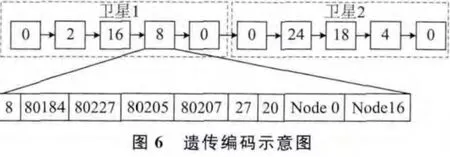
3.2.1 遺傳編碼

由于衛星任務規劃問題中，個體遺傳操作（交叉、變異）涉及到大量的基因位置移動，本文采用實數鏈狀編碼，將衛星按編號順序排列，每顆衛星任務序列包含一對虛擬起始、終止節點，兩者之間所夾節點為該衛星執行的任務節點，相鄰衛星間通過虛擬的起始節點與終止節點連接。為便于遺傳個體的解碼及任務插入的可行性分析，本文設計的任務節點包含以下信息：任務號、占用的可用時間窗口開始時間、占用的時間窗口終止時間、最早開始執行時間、最晚開始執行時間、關鍵任務序列編號、后向能量負荷、指向下一任務節點的指針、指向前一任務節點的指針。具體遺傳編碼示例如圖6所示。

3.2.2 選擇算子

采用二元錦標賽選擇，從種群中隨機選取2個個體，比較這2個個體在非支配排序中的順序，選取位置靠前的個體。

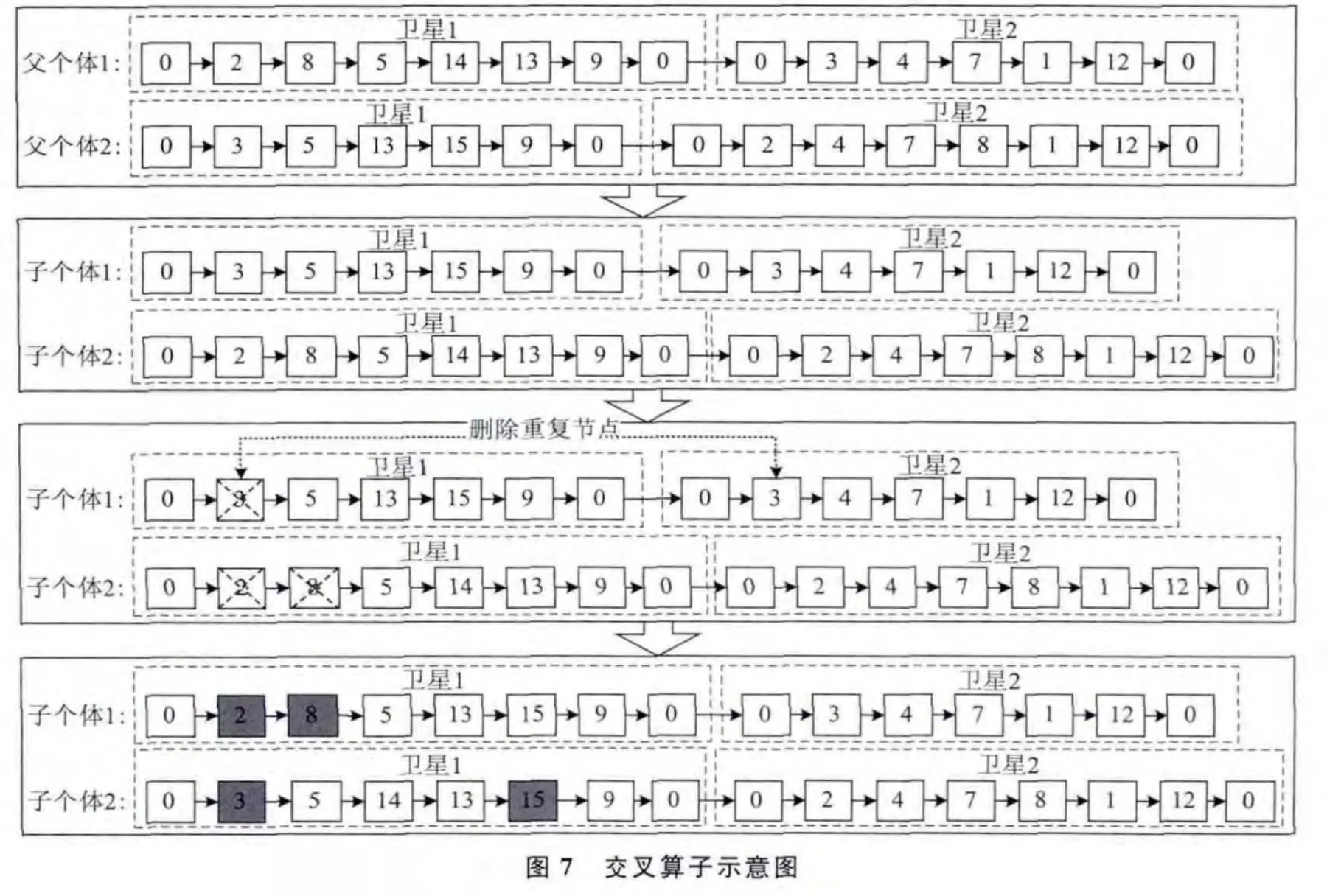
3.2.3 交叉算子

根據上述遺傳編碼，設計交叉算子（圖7）：在兩個父個體上，隨機選擇同一顆衛星的任務序列互相替換；在父個體其他衛星的任務序列上刪除與新替換的衛星任務序列重復的任務；并嘗試插入新替換的衛星任務序列相比原始任務序列丟失的任務。

3.2.4 變異算子

根據成像任務多時間窗口特性，設計單點變異算子，具體工作流程如下：

①對原始任務序列（1，2，3，4…nt）進行隨機排序，初始化任務序列號i＝1；

②計算任務Ti對應的時間窗口數量nitw；

③若nitw＝0，i＝i＋1，轉到（2）；

④若待變異染色體中不存在Ti，嘗試插入任務Ti。若插入成功，更新染色體，結束變異；若插入失敗，i＝i＋1，轉到（2）；

⑤判斷Ti在染色體中的位置能否改變，若能，改變Ti位置，更新染色體，結束變異；否則，刪除Ti，更新染色體，結束變異。

3.3 種群初始化

①初始化任務序列號i＝1，個體編號j＝1，種群大小M；

②初始化調度方案任務鏈Schedulej＝φ，對原始任務序列（1，2，3，4…nt）進行隨機排序；

③選取任務Ti插入，設任務Ti對應的時間窗口數量nitw；

④若nitw＝0，轉到（7）；否則將任務Ti對應的時間窗口進行隨機排序，k＝1；

⑤選取時間窗口TWk，若任務Ti在時間窗口TWk能夠插入到調度方案中而不引起沖突，更新Schedulej，轉到（7）；

⑥k＝k＋1，若k≤nitw，轉（5）；

⑦i＝i＋1，若i＞nt，轉（8）；否則，轉到（3）；

⑧j＝j＋1，若j≤M，i＝1，轉到（2）；否則，種群初始化結束。

4 實驗及分析

4.1 實驗方案設計

假設有2顆衛星，分別選取50，100，200個點目標成像，通過STK軟件計算衛星與觀測目標間的可見時間窗口，并隨機模擬各觀測目標要求的成像時長及任務收益。

常規衛星任務規劃往往僅以任務收益和最大為優化目標，不考慮魯棒性指標。魯棒性任務規劃研究中王軍民［12］提出基于鄰域的魯棒性指標。針對上述不同觀測目標數量的3組輸入數據，將本文提出的基于總時間重疊度及總任務執行時長指標的魯棒性任務規劃方案，分別與常規衛星任務規劃方案和基于鄰域指標的魯棒性任務規劃方案對比分析。

4.2 基于總時間重疊度和總任務執行時長指標的魯棒性衛星任務規劃方案與常規方案對比

針對上述不同觀測目標數量的3組輸入數據，僅以任務收益和最大為優化目標建立衛星任務規劃模型，采用遺傳算法求解；同時以任務收益和最大、總時間重疊度最小、總任務執行時長最短為優化目標建立衛星魯棒性任務規劃模型，采用本文提出的基于NSGA－П的衛星魯棒性任務規劃算法求解。比較每組數據在兩種情況下得到的最優規劃方案任務收益和、總時間重疊度、總任務執行時長3項指標（圖8～圖10，表3～表5），考慮三優化目標得到的Pareto最優解數量較多，僅列出收益指標與單優化目標得到的任務收益和相差10以內的規劃方案指標函數值。

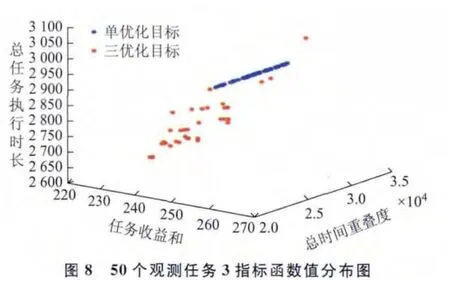
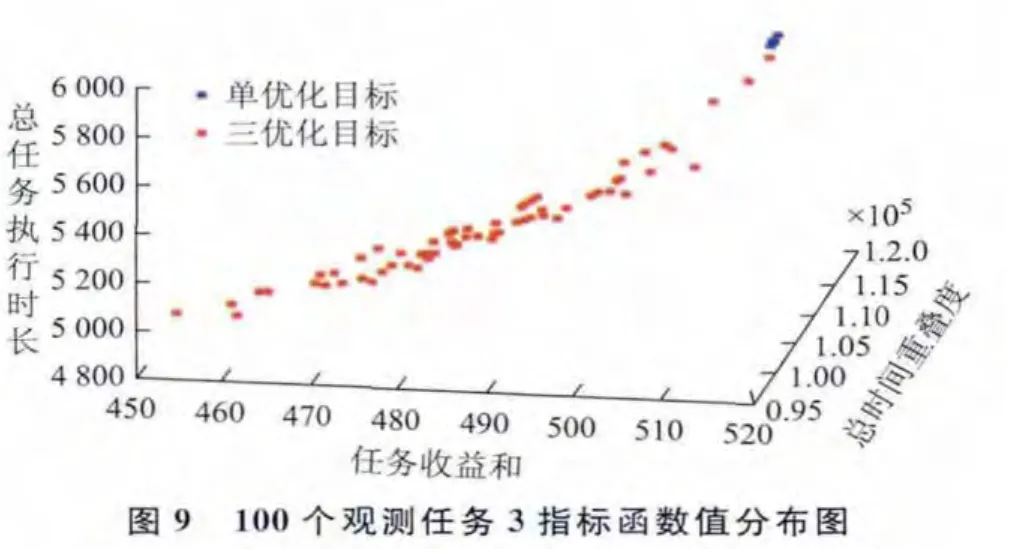
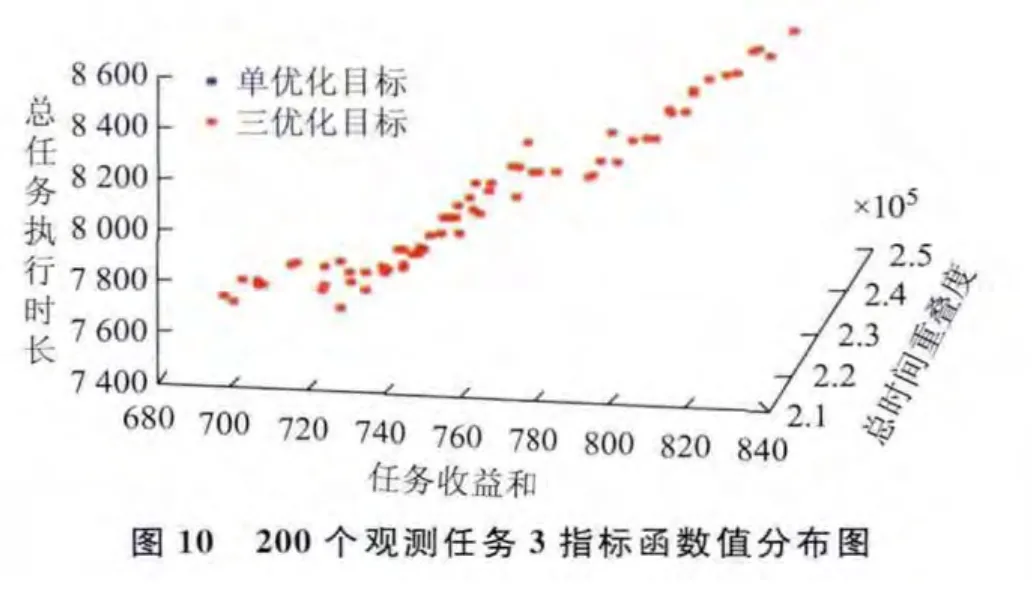
表3 50個觀測任務3指標高收益區具體數值列表

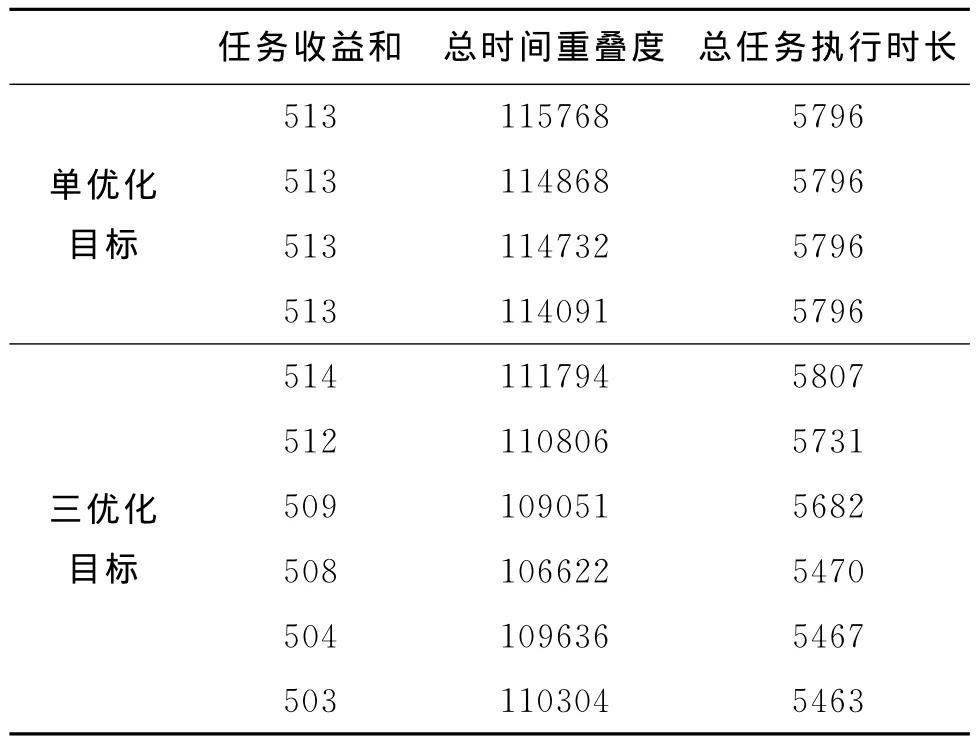
表4 100個觀測任務3指標高收益區具體數值列表

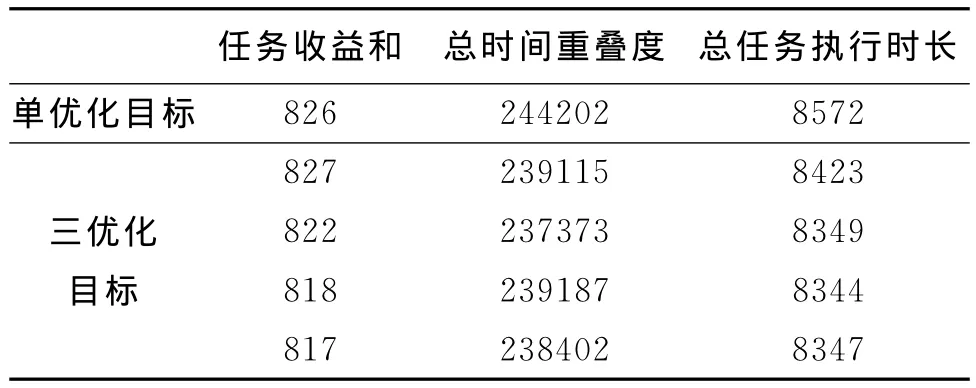
表5 200個觀測任務3指標高收益區具體數值列表

分析圖8～圖10，及表3～表5可知，相比單優化目標思想的常規衛星任務規劃，本文提出的三優化目標方法能得到任務收益和相差不大，但總時間重疊度及總任務執行時長都有大幅度減小的規劃方案。此外，三優化目標方法不容易陷入局部最優，能進化得到任務收益和更大的規劃方案，以及多個高收益、總時間重疊度和總任務執行時長較小的規劃方案供決策者選擇。

4.3 基于總時間重疊度、總任務執行時長指標與基于鄰域指標的魯棒性任務規劃方案對比

針對上述3組實驗數據，分別求解基于鄰域指標與基于總時間重疊度、總任務執行時長指標的兩種衛星魯棒性任務規劃模型，并比較兩種規劃方案的任務收益和、總任務執行時長、方案中可調整的任務收益和指標（圖11～圖16）。

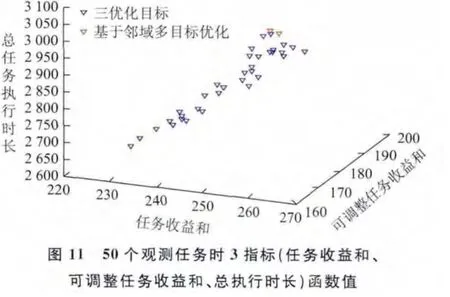
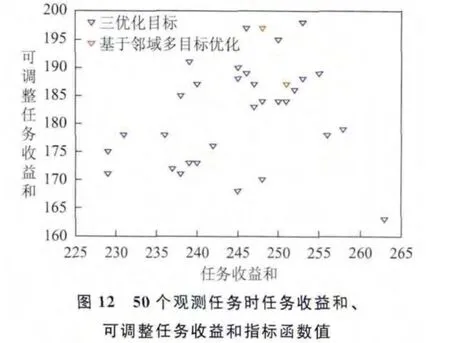
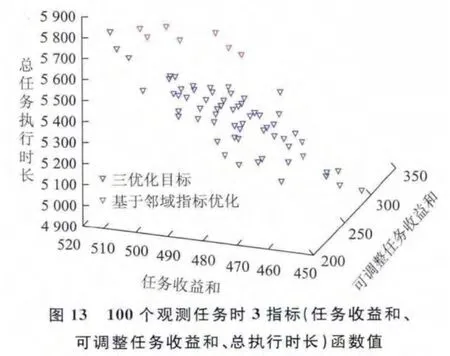
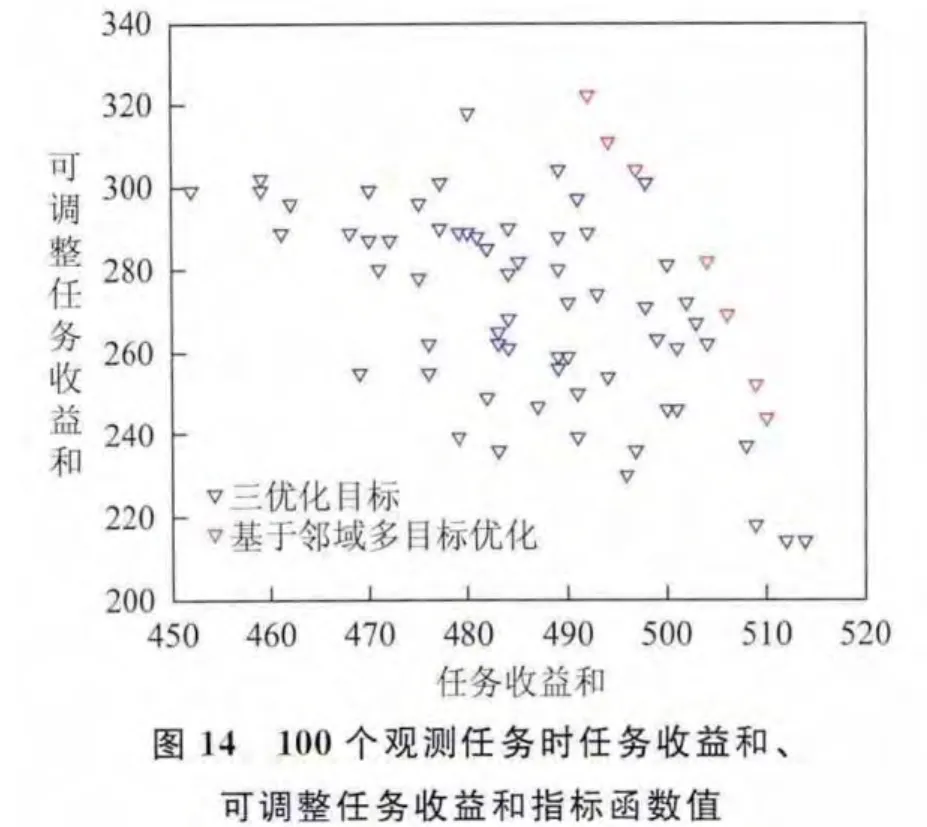
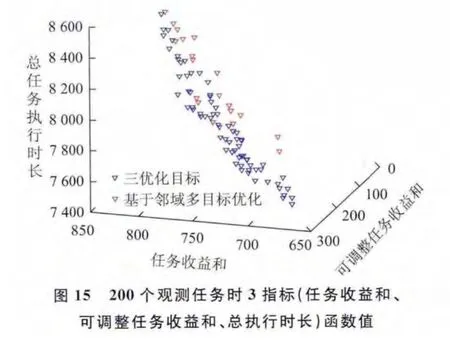
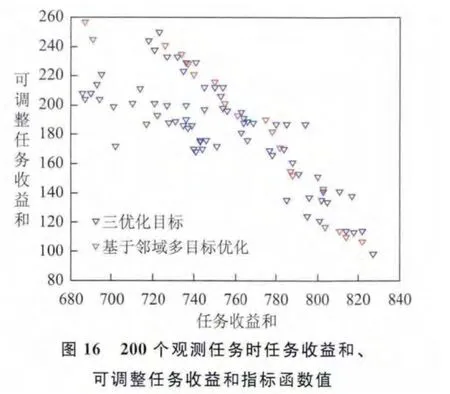
分析圖11～圖16可知，在任務收益和指標值較大時，基于總時間重疊度、總任務執行時長指標與基于鄰域指標的魯棒性任務規劃方案相比，兩種規劃方案的任務收益和、可調整任務收益和指標都相差不大，基于總時間重疊度、總任務執行時長指標得到的規劃方案總任務執行時長更小。

5 結束語

本文提出總任務執行時長、總時間重疊度兩項新魯棒性指標，建立成像衛星魯棒性任務規劃模型，并設計基于NSGA－П的衛星魯棒性任務規劃算法求解該模型。實驗表明，在考慮任務收益和最大化的基礎上，引入總時間重疊度及總任務執行時長的三優化目標模型、僅考慮任務收益和指標的單優化目標模型（常規衛星任務規劃方案）、基于鄰域魯棒性指標的多目標優化模型，三者得到的任務總收益高且相差不大的規劃方案相比，本文方法得到的衛星任務規劃方案總時間重疊度、總任務執行時長往往更小，當新應急任務到來時，將有更長的空余時間段接受其直接插入而不引起沖突，且與其沖突的原始任務能調整到其他時間窗重新安排而不被刪除的概率也更大。此外，總任務時長越短，衛星能量消耗越小，采用本文方法得到的衛星任務規劃方案，在降低衛星能量損耗方面也具有重要實踐意義。

［1］王沛，譚躍進.衛星對地觀測任務規劃問題簡明綜述［J］.計算機應用研究，2008，25（10）：2893－2897.

［2］VASQUEZ M，HAO J K.A “logic－constrained”knapsack formulation and a tabu algorithm for the daily photograph scheduling of an earth observation satellite［J］.Computational Optimization and Applications，2001，20（2）：137－157.

［3］BENSANA E，VERFAILLIE G，LEMAITRE M.Earth observing satellite［J］.Managements Constraints，1999，4（3）：293－299.

［4］FRANK J，SMITH D E.Planning and scheduling for fleets of earth observing satellites［C］.Proceedings of the Sixth International Symposium on Artificial Intelligence，Robotics，Automation and Space，2001.

［5］WOLFE W J，SORENSEN S E.Three scheduling algorithms applied to the earth observing systems domain［J］.Management Science，2000，46（4）：148－168.

［6］GABREL V，VANDERPOOTEN D.Enumeration and interactive selection of efficient paths in a multiple criteria graph for scheduling an earth observing satellite［J］.European Journal of Operational Research，2002，139（3）：533－542.

［7］PEMBERTON J C，GREENWALD L G.On the need for dynamic scheduling of imaging satellites［J］.International Archives of Photogrammetry Remote Sensing and Spatial Information Sciences，2002，34（1）：165－171.

［8］VERFAILLIE G，SCHIEX T.Solution reuse in dynamic constraint satisfaction problems［C］.AAAI，1994，94：307－312.

［9］劉洋，陳英武，譚躍進.一種有新任務到達的多衛星動態調度模型與方法［J］.系統工程理論與實踐，2005，25（4）：35－41.

［10］王軍民，王鵬，李菊芳，等.成像衛星魯棒性調度策略研究［J］.系統工程與電子技術，2010，32（1）：109－114.

［11］DEB K，PRATAP A，AGARWAL S，et al.A fast and elitist multi－objective genetic algorithm：NSGA－II［J］.IEEE Transactions on Evolutionary Computation，2002，6（2）：182－197.

［12］DEBK，AGRAWAL S，PRATAP A，et al.A fast elitist non－dominated sorting genetic algorithm for multi－objective optimization：NSGA－II［J］.Lecture Notes in Computer Science，2000，19（17）：849－858.