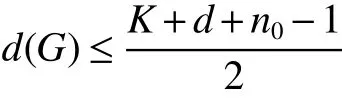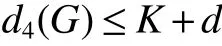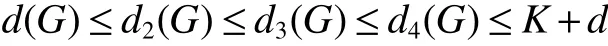Disjoint Paths and k-wide Diameter of Circulants with Degree 4?
LIU Shu-ting,MENG Ji-xiang
(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract: In this paper,we give a family of four internally disjoint paths between any two vertices of the circulant graph with degree 4 by constructing.Moreover,one upper bound of 4-wide diameter of the kind of the circulant graph is also given.
Key words:circulant graph,disjoint paths,k-wide distance,k-wide diameter
0 Introduction and fundamental Definitions
For notation not defined here,see[1]for references.Firstly,we introduce some notions of the circulant graph and give some properties proved in other articles.
Let Zn={0,1,…,n ? 1},S ? Zn? {0}.?S=S(mod n),namely there exist d1,d2,…,dk,such that S={d1,d2,…,dk,n?d1,n?d2,…,n?dk},where d1,d2,…,dkare called spanning elements.In the following,we assume that the points of a graph are labeled clockwise by 0,1,2,…,n?1,(corresponding to 0,?n+1,…,?2,?1 respectively)and we refer to point i instead of saying the point labeled i.
Definition 1The graph G with order n is called circulant graph if it satisfies:
1)V(G)=Zn;
2)E(G)={ij|j?i∈S},where the operation takes module n.
The circulant graph G is denoted by Cn(d1,d2,…,dk)or brie fly Cn(di),where 0 Definition 2Given a graph G,for x,y∈V(G),x,y,let Pk(x,y)be a family of k internally disjoint paths between x and y,i.e. where|p1|≤ |p2|≤…≤ |pk|and|pi|denotes length of the path pi,i=1,2,…,k.The k-wide distance dk(x,y)between vertices x and y is the minimum|pk|among all Pk(x,y)and k-wide diameter dk(G)of G is defined as the maximum k-wide distance dk(x,y)over all pairs(x,y)of vertices of G. If a graph G is k-connected,according to Menger’s Theorem,any pair of two distinct vertices x and y has a Pk(x,y).This means that dk(G)exists if G is k-connected. Proposition 1Znis a residue class ring mod n.if a,b∈Znand 0 Proposition 2[2]d1(G)≤ d2(G)≤…≤ dk(G)for any network G of connectivity κ. Theorem 1[3]Cn(d1,d2,…,dk)is connected if and only if gcd(d1,d2,…,dk,n)=1. Theorem 2[4]If Cn(d1,d2,…,dk)is a connected circulant of degree 4 or 6,then κ=δ. Theorem 3[5]If gcd(n,a)=1 or gcd(n,b)=1,then there exists an integer k satisfying Cn(1,k)?Cn(a,b). In general,we can show that a circulant is connected by identifying the existence of a path from 0 to t for each vertex t.That is,we need a combination of elements of S that sum to t:t(mod n),where(αm)and[dm]respectively denote step number and step factor of the 0t-path. Let G=Cn(1,d)(n≥6)be a circulant graph,then one of all the families of 4 internally disjoint paths from 0 to t for each vertex t,denoted by P4(0,t),can be constructed under the following conditions which the lemmas should satisfy.Firstly,we give the conditions: (1)Give afixed pair of integers(n,d)and let them satisfy n=Kd+n0,where 1K>2. (2)?0 Lemma 1Let G=Cn(1,d)(n≥6)be a circulant graph,then the connectivity of G is 4. Proof By Theorem 1,we knowthatG is connected with degree 4,By Theorem 2,we obtain that the connectivity of G is 4. Lemma 2If k,0 and i,0,then a P4(0,t)can be constructed as follows: t(1):(k)[d]+(i)[1]=t;t(2):(i)[1]+(k)[d]=t; t(3):(K?k)[?d]+(n0?i)[?1]=t?n,t(4):(n0?i)[?1]+(K?k)[?d]=t?n,where i t(3):(K?k?1)[?d]+(d?i+n0)[?1]=t?n,t(4):(d?i+n0)[?1]+(K?k?1)[?d]=t?n,where i>n0; t(3):(K?k)[?d]=t?n,t(4):(d?1)[?1]+(K?k?1)[?d]+(1)[?1]=t?n,where i=n0. In the expressions,note that t(l)denotes the l-th disjoint path from 0 to t,where l={1,2,3,4}.Elements in the parentheses represent step numbers.Elements,such as 1,?1,d,?d,in the brackets represent step factors of the path.For example,t(l)denotes the path(d,2d,…,kd,kd+1,…,kd+i).the others have the same Definition. Lemma 3If k=0 and i,0,then a P4(0,t)can be constructed as follows: t(1):(i)[1]=t;t(2):(1)[d]+(d?i)[?1]=t;t(3):(d?i)[?1]+(1)[d]=t; t(4):(K?2)[?d]+(n0?i)[?1]+(2)[?d]=t?n,where n0≥i>0; t(4):(K?2)[?d]+(i?n0)[?1]+(2)[?d]=t?n,where i>n0>0; t(4):(K?2)[?d]+(d?i)[?1]+(1)[?d]=t?n,where i>n0=0. Lemma 4If i=0 and k,0,then a P4(0,t)can be constructed as follows: t(1):(k)[d]=t;t(2):(1)[1]+(k)[d]+(1)[?1]=t; t(3):(1)[?1]+(k)[d]+(1)[1]=t; t(4):(K?k?1)[?d]+(n0)[?1]+(1)[?d]=t?n,where n0>i=0; t(4):(K?k)[?d]=t?n,where n0=i=0. The method to prove any two paths are internally disjoint in the different cases are similar.So we will only prove some cases without repeating the methods to prove other cases here. ProofIn order to prove that two arbitrary paths are internally disjoint,we only need to prove that,(mod n)between arbitrary l-th path and m-th path,for arbitrary variables ξ and η,where m,l∈{1,2,3,4}.Wheredenote the sum to η terms of t(l).The sum to η terms about disjoint paths are defined as And if i<ξ≤i+k,we obtain because 0 By the monotone increasing properties of Our main theorems are as follows. Theorem 4Let G=Cn(1,d)(n≥6,d≥2)be a circulant graph,then where K=bn/dc>2. ProofIn order to obtain one upper bound of d(0,t)=min{|pi|:for all the paths from 0 to t},we can calculate the minimum sum of step numbers of every path from 0 to t through its corresponding four disjoint paths constructed above. Case 1k,0,i,0, If i If i>n0,then d(0,t)≤min{k+i,K?k?1+d?i+n0}≤(k+i+K?k?1+d?i+n0)/2=(K?1+d+n0)/2; If i=n0,then d(0,t)≤min{k+i,K?k,K?k+d?1}=min{k+n0,K?k}≤(k+n0+K?k)/2=(K+n0)/2. Case 2k=0,i,0, If n0≥i>0,then d(0,t)≤min{i,d?i+1,K+n0?i}≤(i+d?i+1)/2=(d+1)/2.; If i>n0>0,then d(0,t)≤min{i,d?i+1,K+i?n0}≤(i+d?i+1)/2=(d+1)/2.; If i>n0=0,then d(0,t)≤min{i,d?i+1,K+d?i?1}≤(i+d?i+1)/2=(d+1)/2. Case 3k,0,i=0, If n0>i=0,then d(0,t)≤min{k,k+2,K+n0?1?k}=min{k,K+n0?k}≤(K+n0)/2; If n0=i=0,then d(0,t)≤min{k,k+2,K?k}=min{k,K?k}≤K/2; In the above cases,we obtain that d(G)=max{d(0,t):t∈V(G)}≤max{(K+n0)/2,(K?1+d+n0)/2,(d+1)/2,K/2}=(K+d+n0?1)/2. Theorem5 Let G=Cn(1,d)(n≥6,d≥2)be a circulant graph,then where K=bn/dc>2. ProofIn order to obtain one upper bound of d4(0,t)=min{max{|t(i)|:t(i)∈P4(0,t)}:for all P4(0,t)},we calculate the maximum sum of step numbers of every path from 0 to t through its corresponding four disjoint paths constructed above. Case 1k,0,i,0. If i If i>n0,then d4(0,t)≤max{k+i,K?k?1+d?i}≤max{k+i,K+d}≤K+d; If i=n0,then d4(0,t)≤max{k+i,K?k,K?k+d?1}≤max{k+i,K+d}≤K+d. Case 2k=0,i,0, If n0≥i>0,then d4(0,t)≤max{i,d?i+1,K+n0?i}≤K+d; If i>n0>0,then d4(0,t)≤max{i,d?i+1,K+i?n0}≤K+d; If i>n0=0,then d4(0,t)≤max{i,d?i+1,K+d?i?1}≤K+d. Case 3k,0,i=0, If n0>i=0,then d4(0,t)≤max{k,k+2,K+n0?k}=max{k+2,K+n0?1?k}≤K+d; If n0=i=0,then d4(0,t)≤max{k,k+2,K?k}=max{k+2,K?k}≤K+d; From the above cases,we deduce that d4(G)=max{d4(0,t):t∈V(G)}≤K+d. Corollary 1Let Cn(1,d)(n≥6,d≥2)be a circulant graph,then where K=bn/dc>2.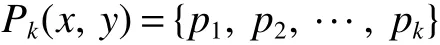
1 Internally disjoint paths
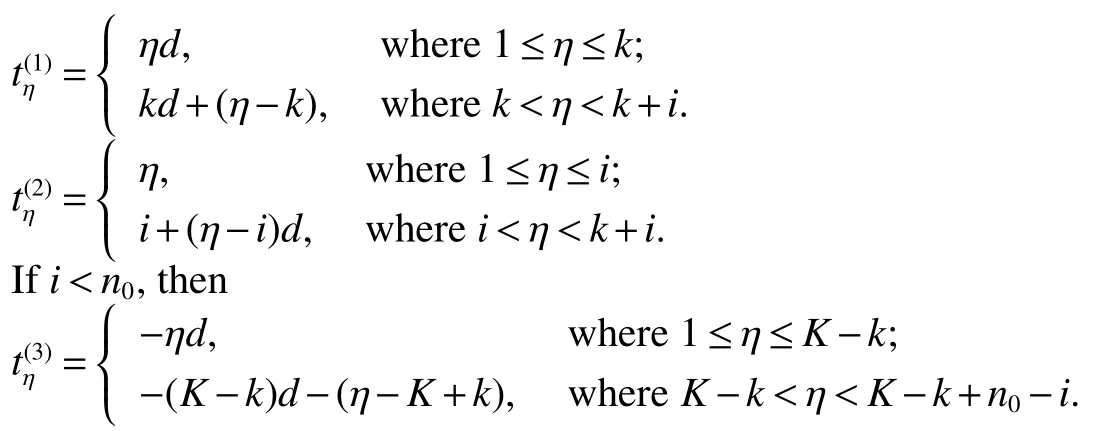
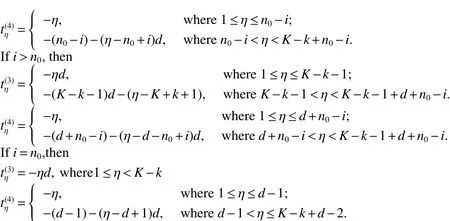
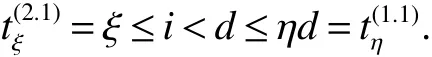
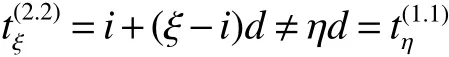
2 k-wide Diameter