一類SIRS傳染病模型的新Lyapunov函數(shù)?

湯倩,滕志東

(新疆大學(xué)數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院，新疆烏魯木齊830046)

0 引言

在傳染病動力學(xué)模型的理論研究中,易感者-染病者-移出者(SIR)型的倉室傳染病模型得到了廣泛研究.根據(jù)Kermack和McKendrick的假設(shè)[3],種群數(shù)量被分為三個不同的類:易感者類(S),染病者類(I)和移出者類(R).易感者與染病者通過接觸致使染病從而進(jìn)入染病者類,而染病者經(jīng)過治療等措施治愈后進(jìn)入移出者類,若移出者得到的免疫能力是永久的,則他將永遠(yuǎn)停留在移出者類.基于這些假設(shè),可以得到相應(yīng)的SIR傳染病動力學(xué)模型.若我們還假設(shè)移出者的免疫能力不是永久的,即移出者經(jīng)過一定的時間可能會失去免疫能力而再次進(jìn)入易感者類,則可得到相應(yīng)的SIRS傳染病動力學(xué)模型.

在文獻(xiàn)[1,2,4,5,6,7]中對不同形式(如具有標(biāo)準(zhǔn)發(fā)生率,指數(shù)出生,常數(shù)移民,總?cè)丝跒槌?shù)或非常數(shù)等)的SIR和SIRS模型的平衡點(diǎn)做了深入的研究,得到了相應(yīng)的無病平衡點(diǎn)的全局穩(wěn)定性和地方病平衡點(diǎn)的局部及全局穩(wěn)定性.特別地文獻(xiàn)[1]中作者研究了如下形式的SIRS傳染病模型

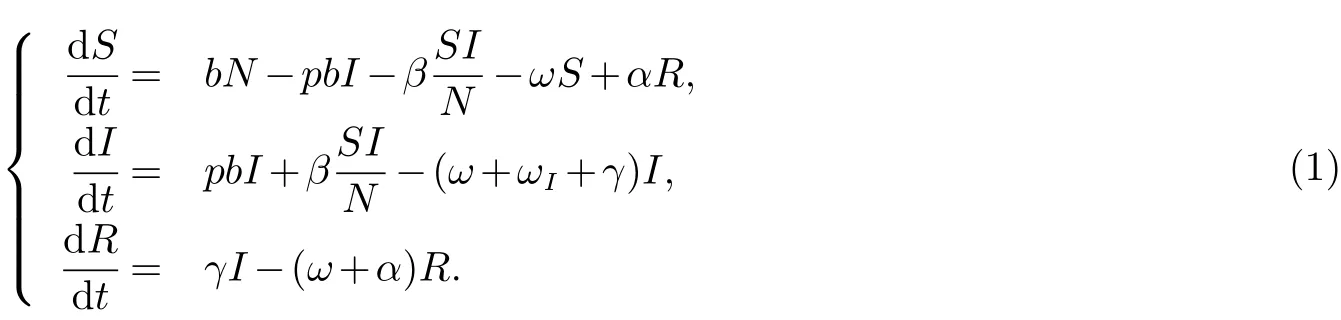
在總?cè)丝跀?shù)N為常數(shù)的假設(shè)下,作者將模型(1)改寫為一個二維系統(tǒng)(參見文獻(xiàn)[1]中方程(3)),通過建立一個Lyapunov函數(shù)V(I,R)=I?I?lnI+a(R?R?)2得到了模型(1)的地方病平衡點(diǎn)(I?,R?)的全局穩(wěn)定性.

基于以上的研究工作,首先考慮如下帶有雙線性發(fā)生率且只有易感具有常數(shù)輸入的SIRS傳染病模型

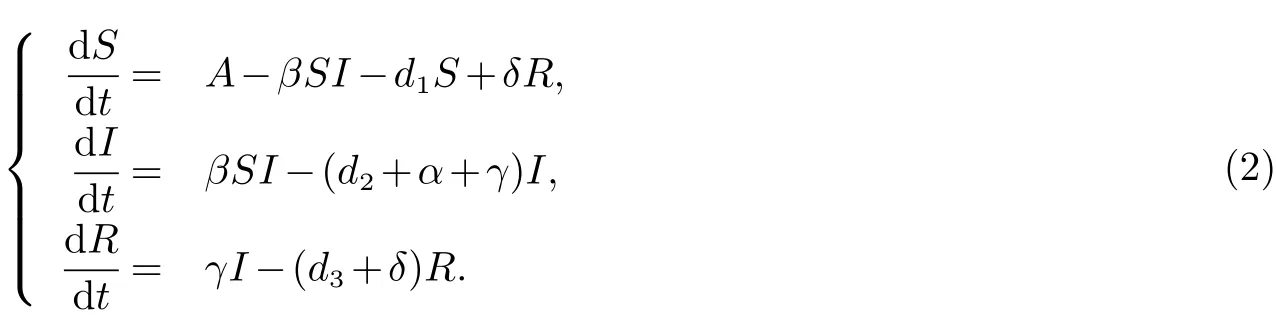
可以證明在模型(2)的地方病平衡點(diǎn)存在的條件下,通過建立一個新的Lyapunov函數(shù)可得到無其他附加條件下模型(2)地方病平衡點(diǎn)的全局穩(wěn)定性.

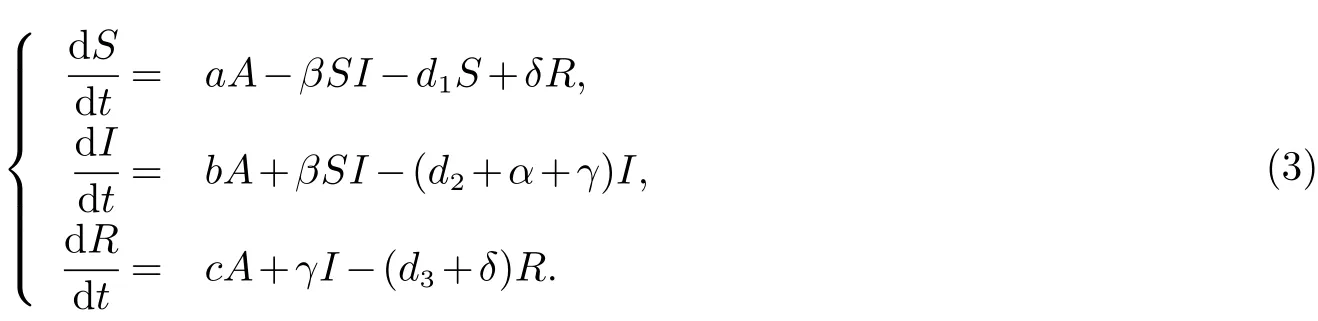
其次,還將討論如下易感者,染病者和移出者都具有常數(shù)移民輸入的SIRS傳染病模型可以證明,當(dāng)模型(3)的地方病平衡點(diǎn)存在時,通過建立一個新的Lyapunov函數(shù)可得到無其他附加條件下模型(3)地方病平衡點(diǎn)的全局穩(wěn)定性.

本文主要包括3節(jié)內(nèi)容:第1節(jié)為引言部分,給出所研究模型的背景以及所要研究的主要內(nèi)容;第2節(jié)和第3節(jié)通過建立新的Lyapunov函數(shù)分別證明了模型(2)和模型(3)地方病平衡點(diǎn)的全局漸近穩(wěn)定性.

1 模型(2)的全局漸近穩(wěn)定性

在模型(2)中,S(t),I(t),R(t)分別為某一地區(qū)內(nèi)在時刻t的易感者,染病者和移出者人群的數(shù)量,A是總?cè)丝诘某?shù)輸入率,d1,d2,d3分別是易感者,染病者和移出者的自然死亡率,α是因病死亡率,β是疾病的傳染系數(shù),γ是染病者的恢復(fù)系數(shù),δ是移出者失去免疫力回到易感者的免疫率系數(shù).我們假設(shè)A,β,γ和δ+d3>0.模型(2)總是存在一個無病平衡點(diǎn)當(dāng)基本再生數(shù)1 時,模型 (2)還存在唯一的地方病平衡點(diǎn)其中

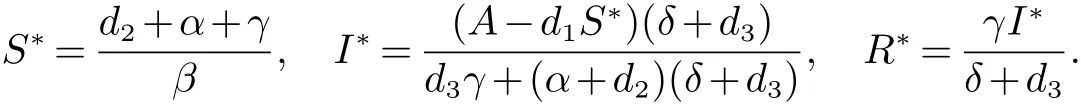
關(guān)于模型(2)解的正性,我們?nèi)菀椎玫疆?dāng)初值S(0)>0,I(0)>0,R(0)>0時,解S(t)>0,I(t)>0,R(t)>0對一切t≥0成立.而關(guān)于模型(2)的地方病平衡點(diǎn)E?的全局穩(wěn)定性我們有如下結(jié)論:

定理1當(dāng)R0>1時,模型(2)的地方病平衡點(diǎn)E?是全局漸近穩(wěn)定的.

證明模型(2)的地方病平衡點(diǎn)E?滿足如下方程

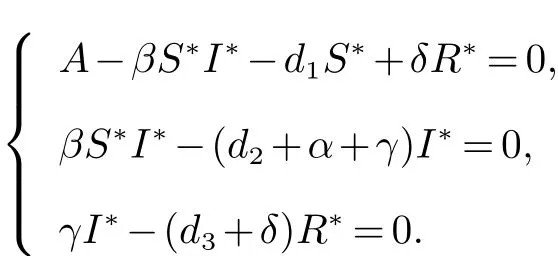
因此,模型(2)可以改寫為如下形式

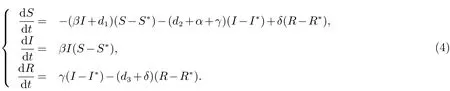
構(gòu)造Lyapunov函數(shù)如下

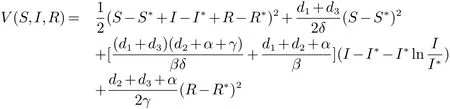
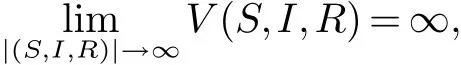
當(dāng)模型(2)中d1=d2=d3=μ時,模型(2)退化為如下模型

因此,作為定理1的推論有如下結(jié)論:

推論1對于模型(5),當(dāng)時,模型(5)存在地方病平衡點(diǎn)且它是全局漸近穩(wěn)定的.

顯然,推論1改進(jìn)了文獻(xiàn)[1，2]中關(guān)于模型(5)的相關(guān)結(jié)論(參見文獻(xiàn)[1]及文獻(xiàn)[2]中定理3.2.1).

2 模型(3)的全局漸近穩(wěn)定性

在模型(3)中,A表示進(jìn)入該地區(qū)的總移民率,參數(shù)a>0,b≥0,c≥0分別表示易感者,染病者和移出者的常數(shù)輸入比例且滿足a+b+c=1,其余參數(shù)含義與模型(2)相同.我們假設(shè)d1,d2,d3,α,δ≥0,A,β,γ和δ+d3>0,且d1≤min(d2,d3).

關(guān)于模型(3)解的正性,我們?nèi)菀椎玫疆?dāng)初值S(0)>0,I(0)>0,R(0)>0時,解S(t)>0,I(t)>0,R(t)>0對一切t≥0成立.對于模型(3)的地方病平衡點(diǎn)的全局漸近穩(wěn)定性,我們將分兩種情況:b=0和b>0進(jìn)行討論.

2.1 情形1:b=0

此時,模型(3)具有如下形式

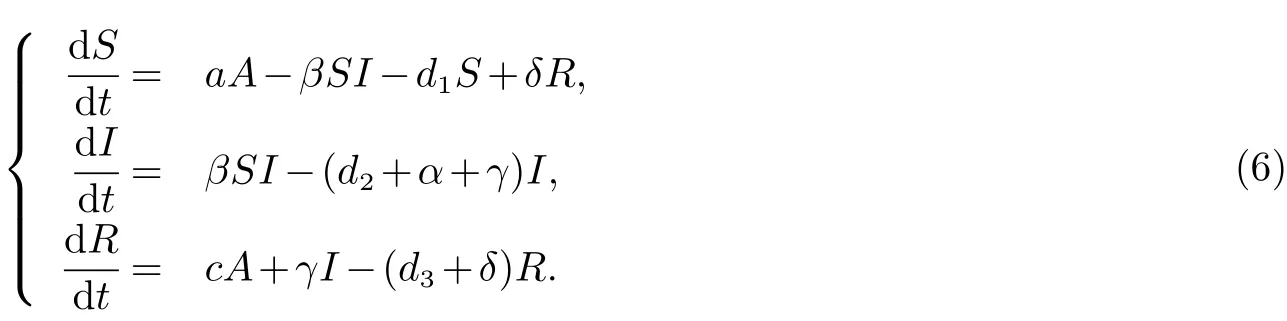
此情形下,沒有染病者輸入.顯然,模型(6)總是存在一個無病平衡點(diǎn)并且,當(dāng)基本再生數(shù)1 時,模型 (6)還存在唯一的地方病平衡點(diǎn) E?=(S?,I?,R?),其中

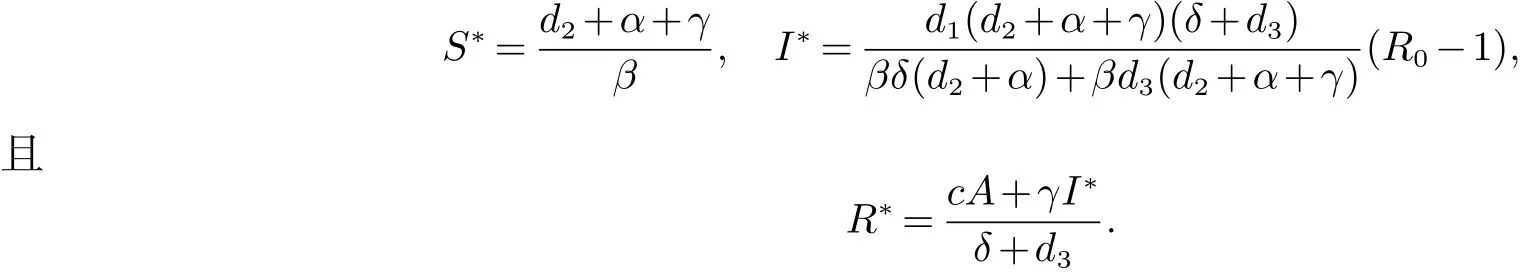
關(guān)于模型(6)的地方病平衡點(diǎn)E?的全局穩(wěn)定性有如下結(jié)論:

經(jīng)不同教學(xué)模式后，實(shí)驗(yàn)組和對照組學(xué)生滿意度分別為96.15%，69.23%，組間比較，差異具有統(tǒng)計學(xué)意義（P＜0.05），見表4。

定理2當(dāng)R0>1時,模型(6)的地方病平衡點(diǎn)E?是全局漸近穩(wěn)定的.

事實(shí)上,模型(6)的地方病平衡點(diǎn)E?滿足如下方程

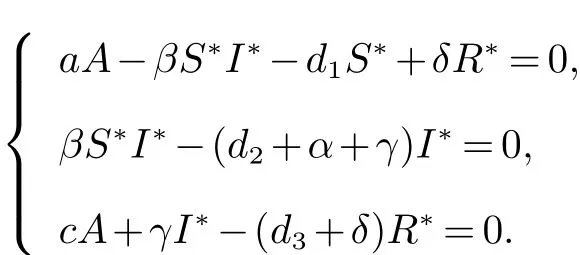
因此,模型(6)可以改寫為如下形式

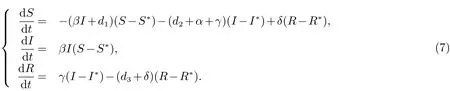
此時方程(7)與方程(4)相同,構(gòu)造與同定理1相同的Lyapunov函數(shù)V(S,I,R),則證明過程與定理1相同,此處省略.

2.2 情形2:b>0

在b>0的情形下,關(guān)于模型(3)平衡點(diǎn)的存在性,我們有如下結(jié)論:

定理3模型(3)在b>0時,不存在無病平衡點(diǎn),但總存在一個地方病平衡點(diǎn)E?=(S?,I?,R?),其中

并且,I?是如下方程唯一的解:

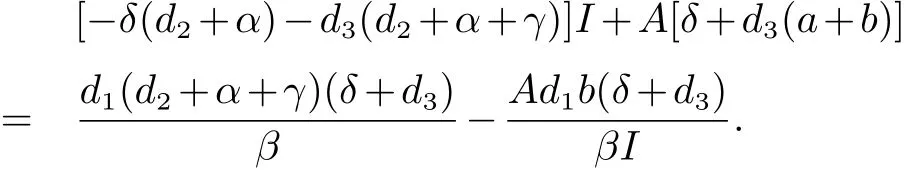
證明知模型(3)的平衡點(diǎn)滿足如下方程

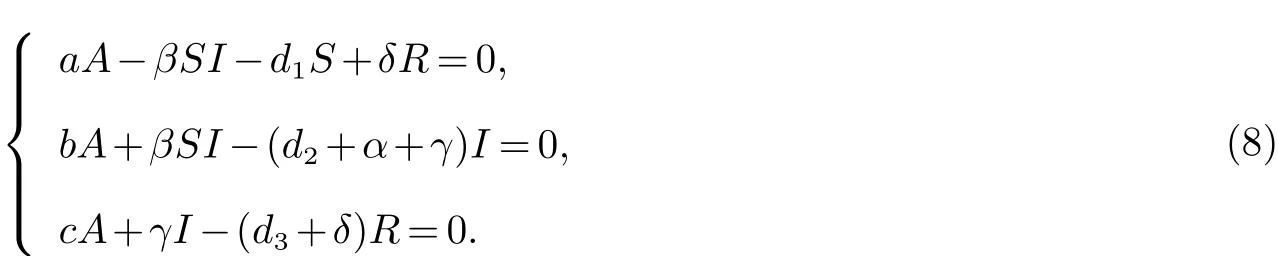
若模型(3)的無病平衡點(diǎn)存在,則由(8)的第二個方程知,bA=0,于是有b=0或A=0,此與前面的假設(shè)b>0,A>0矛盾,故在b>0時模型(3)的無病平衡點(diǎn)不存在.

設(shè)E?=(S?,I?,R?)是模型(3)的地方病平衡點(diǎn),則其滿足方程(8),由方程(8)的第二和第三個方程解得

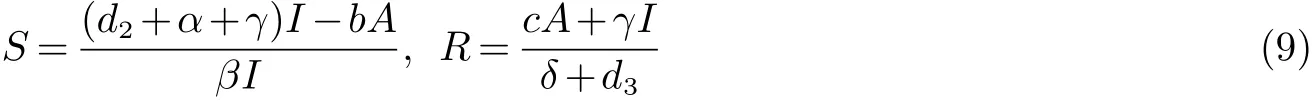
將(9)代入(8)的第一個方程,整理可得

由于?0(I)=?δ(d2+α)?d3(d2+α+γ)≤0,所以?(I)是關(guān)于I的非增函數(shù),可知計算得

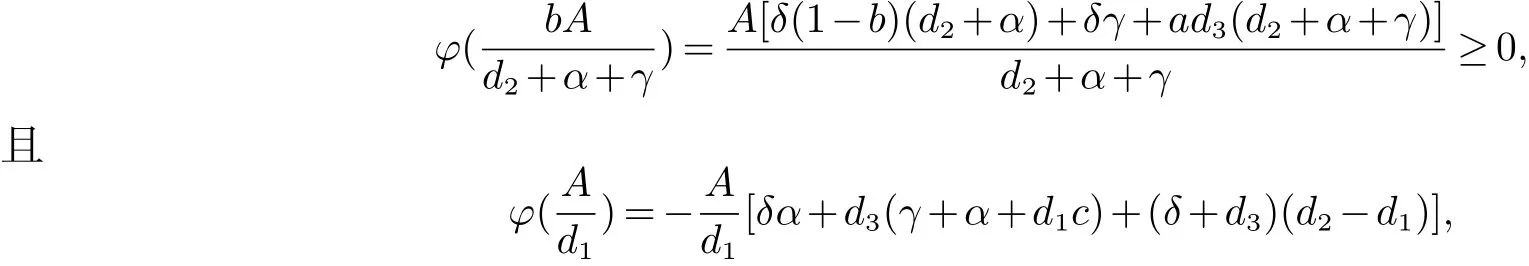
由假設(shè)d1≤min(d2,d3)知d2?d1≥0,則有

類似地,計算得

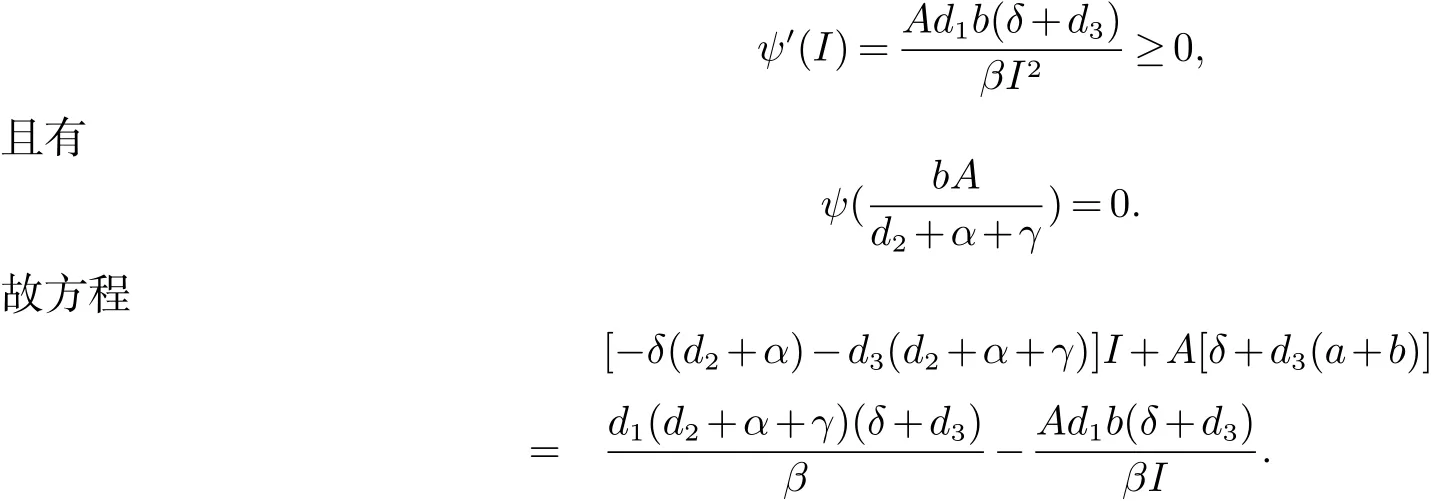
關(guān)于模型(3)的地方病平衡點(diǎn)E?的全局穩(wěn)定性有如下結(jié)論:

定理4模型(3)的地方病平衡點(diǎn)E?是全局漸近穩(wěn)定的.

證明將模型(3)改寫為如下形式

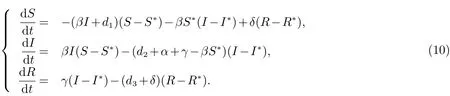
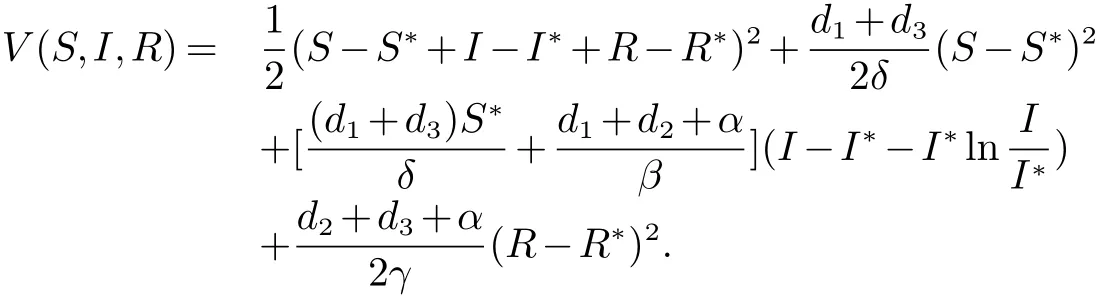
構(gòu)造Lyapunov函數(shù)如下類似于定理1的證明，易知V(S,I,R)是一個Lyapunov函數(shù).將V(S,I,R)沿系統(tǒng)(10)關(guān)于t微分,計算得

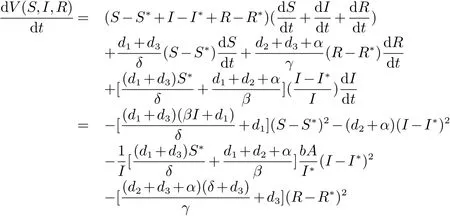
特別地,當(dāng)模型(3)中d1=d2=d3=μ時,作為定理2和定理4有如下結(jié)論:

推論2對于模型(3),若d1=d2=d3=μ,則如下結(jié)論成立:

(2).當(dāng)b>0時,模型(3)存在地方病平衡點(diǎn)且它是全局漸近穩(wěn)定的.

顯然,當(dāng)文獻(xiàn)[2]中傳染率系數(shù)β(N)=β為常數(shù)時,推論2改進(jìn)了文獻(xiàn)[1,2]中關(guān)于模型(11)的相關(guān)結(jié)論(參見文獻(xiàn)[1]及文獻(xiàn)[2]中定理3.2.3?定理3.2.6).