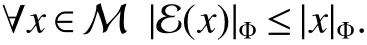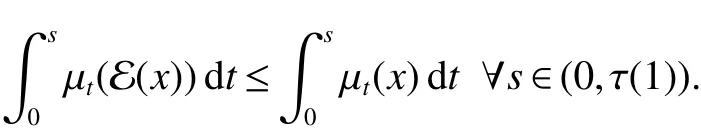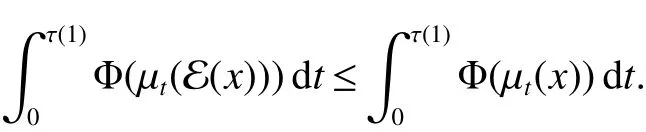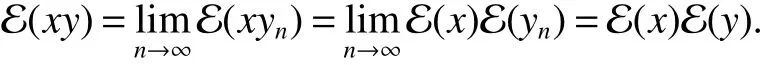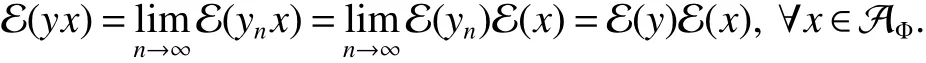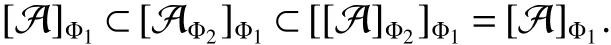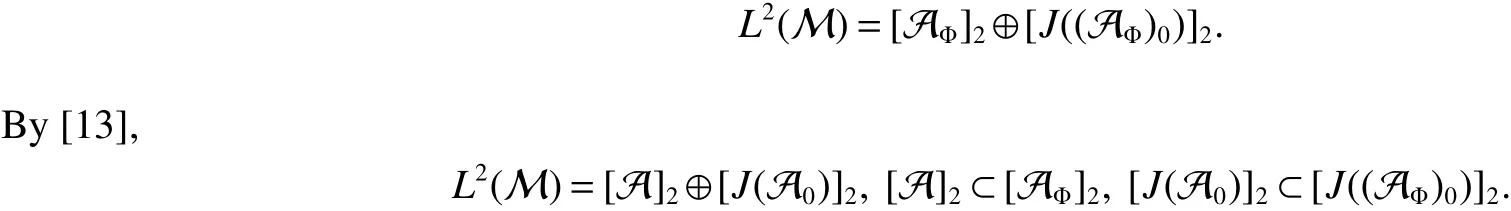Characterization of Subdiagonal Algebras on Noncommutative Orlicz Spaces?
Abdugheni Abdurexit
(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract: Let Φ be a growth function,M befinite von Neumann algebra with a faithful normal tracial state τ and A be a tracial subalgebra of M.We proved contractivity of conditional expectation E and A has LΦ-factorization if and only if A is a subdiagonal algebra.We also gave some characterizations of subdiagonal algebras.
Key words:tracial subalgebra,subdiagonal algebra,growth function,L2-density,LΦ-factorization
0 Introduction
In[1],Arveson introduced the notion offinite,maximal,subdiagonal algebra A of M,as noncommutative analogues of weak?-Dirichlet algebras.After the Arveson’s work,several authors studied the noncommutative Hardy spaces associated with such algebras([2-7]).Arveson proved a Szeg?’s type factorization theorem.Some extensions can be found in[8-10].Labuschagne[11]proved a noncommutative version of Szeg?’s theorem.In recent notes[5,12,13],among other things,Blecher,Labuschagne and Bekjan studied tracial subalgebra of M and gave several characterizations of subdiagonal algebras.Blecher and Labuschagne proved that if tracial subalgebra A has L∞-factorization if and only if A is a subdiagonal algebra and Bekjan[13]proved the Lp-factorization(0 Throughout this paper,we denote by M afinite von Neumann algebra on a Hilbert spaces with a faithful normal tracial state τ.Given a von Neumann subalgebra N of M,an expectation E:M → N is defined to be a positive linear map which preserves the identity and satisfies E(xy)=xE(y)for all x∈N and y∈M.Since E is positive it is hermitian,i.e.E(x)?=E(x?)for all x∈M.Hence E(yx)=E(y)x for all x∈N and y∈M.In order to get a more profound study of E we reference the readers to[1,7]. Definition 1Let A be a weak?closed unital subalgebra of M.If there is a linear projection E from A onto D=A∩J(A)such that (i)E is multiplicative on A,i.e.E(ab)=E(a)E(b)for all a,b∈A; (ii)τ?E=τ, then A is called a tracial subalgebra of M. Definition 2Let A be a weak?closed unital subalgebra of M and let E be a normal faithful conditional expectation from M onto a von Neumann subalgebra D of M.A is called a subdiagonal algebra of M with respect to E if the following conditions are satisfied (i)A+J(A)is weak?dense in M; (ii)E(ab)=E(a)E(b)for all a,b∈A; (iii)D=A∩J(A). Let A0=A∩ker(E).We call A is τ-maximal,if Definition 3We say a function Φ is a growth function,if Φ is a continuous and nondecreasing function from[0,∞)onto itself.In this paper we always assume that for a growth function Φ,tΦ0(t)is also a growth function and define the following quantitative indices: We say that Φ is a strict convex growth function if pΦ>1 and Φ is a strict concave growth function if qΦ<1. Definition 4(i)A growth function Φ obeys ?2-condition for all t>0,written often as Φ ∈ ?2,if there is a constant K>1 such that Φ(2t)≤KΦ(t). (ii)A growth function Φ said to satisfy the-condition for all t>0,denoted symbolically asif there is a constant 0 Definition 5Let Φ1,Φ2be the growth functions and they have Φ1? Φ2,if for each ε>0 there is a K>0 and an t0≥ 0,such that Definition 6Let Φ be a growth function.We define the corresponding noncommutative Orlicz space on(M,τ)by For x∈LΦ(M),define For more information about noncommutative Orlicz spaces associated with growth function,see[3].For a subset K of LΦ(M),set J(K)={x?:x∈ K},K?1={x:x,x?1∈ K},K+={x:x≥ 0,x∈ K}and[K]Φthe closed liner span of K in LΦ(M). We know that E can be extended to a contractive projection from Lp(M)onto Lp(D)for every 1≤p≤∞.Here we give the general results of contractivity of E from LΦ(M)onto LΦ(D)for every convex growth functions Φ. Theorem 1Let Φ be a convex growth function.Then Consequently,E extends to a contractive projection from LΦ(M)onto LΦ(D).The extension is still denoted by E. ProofFrom the Proposition 3.9 of[7],we know that E(x)is submajorized by x,for all x∈L1(M).Then By Lemma 4.1 of[13], That is τ(Φ(|E(x)|))≤ τ(Φ(|x|)).Thus|E(x)|Φ≤ |x|Φ?x∈ M. By continuity of E we know that the norm inequality|E(x)|Φ≤ |x|Φholds for all x∈ LΦ(M).Thus E extends to a contractive projection from LΦ(M)onto LΦ(D). Let A be a tracial subalgebra of M.For a growth function Φ,we write AΦfor[A]Φ∩M. Lemma 1Let A be a tracial subalgebra of M.Let Φ be a strict convex growth function and Φ ∈ ?2.Then AΦis a tracial subalgebra of M. ProofFirst,we prove that AΦis weak?closed in M.Indeed,suppose that there is x∈M in the weak?closure of[A]Φbut not in[A]Φ.It is easy to check that strict convex growth function Φ is an N-function,since we have tpΦ≤ Φ(t)≤ tqΦfor t≥ 0.Then by Lemma 3.7 and Lemma 3.4 of[4],we couldfined z∈ LΨ(M)? L1(M)such that τ(zx),0 and τ(zy)=0 for every y∈[A]Φ,where Ψ is a complementary function of Φ.Since x is in the weak?closure of[A]Φ,τ(zx)=0.This contraction shows that x∈AΦ. It is clear thatAΦis unital. To see that AΦis an subalgebra,wefirst check that if x∈A,y∈AΦ,then xy∈AΦ.Indeed,if(yn)?A with yn→y in LΦ(M),then xyn∈A and xyn→ xy in LΦ(M).If x∈AΦ,y∈AΦ,then there is(xn)?A such that xn→ x in LΦ(M).Hence xny→xy in LΦ(M),so xy∈AΦ,since xny∈AΦ. Next we prove the productivity of E.Let y∈AΦ,then there is a sequence(yn)?A such that yn→y in LΦ(M).So for all x∈A we have xyn∈A,and xyn→xy in LΦ(M).Thus,by Theorem 1, Hence,by what we just proved, Definition7Let A be a tracial subalgebra of Mand Φbe a growth function.Wesay that A has LΦ-factorization,if for x∈ LΦ(M)?1,there is a unitary u∈M and a∈such that x=ua. Proposition 1Let A be a tracial subalgebra of M.Let growth functions Φ1,Φ2which obey the ?2and ?1 2-conditions have such ordering Φ1?Φ2.If A has LΦ2-factorization,then A has LΦ1-factorization. ProofLet x ∈ M?1? LΦ2(M)?1.Then there exist a unitary u ∈ M and a ∈such that x=ua,since A has LΦ2-factorization.2,and therefore AΦ2has L∞-factorization.By Theorem 1.1 of[5],AΦ2is a subdiagonal subalgebra of M.Let x∈LΦ1(M)?1.From Theorem 3.2 of[3],there exist a unitary u∈M andsuch that x=ua.On the other hand,we have Theorem 2Let A be a tracial subalgebra of M.Then the following conditions are equivalent: (i)A is a subdiagonal subalgebra of M. (ii)For all growth functions Φ which satisfy the?2and ?12-conditions,A has LΦ-factorization. (iii)For some strict convex growth functions Φ which satisfy the ?2-conditions,A has LΦ-factorization. Proof(i)?(ii)follows from the Theorem 3.2 of[3]. (ii)?(iii)is clear. (iii)?(i).Let Φ be a convex growth functions and A has LΦ-factorization.By ordering we know that L1(M)?LΦ(M).From the Proposition 3.4,we get that A has L1-factorization.Then by the Theorem 2.4 of[13],A is a subdiagonal subalgebra of M. Theorem 3Let A be a τ-maximal tracial subalgebra of M.Then the following conditions are equivalent: (i)A is a subdiagonal subalgebra of M. (ii)For some growth functions Φ which satisfy the?2and ?12-conditions,A has LΦ-factorization and AΦis a tracial subalgebra of M. ProofWe only need to prove(ii)?(i).By the proof of Proposition 3.4,we know that AΦis a subdiagonal subalgebra of M and A ? AΦ.If y ∈ AΦ,then τ(xy)= τ(E(xy))= τ(E(x)E(y))=0 for each x ∈ A0.From the τ-maximality of A we know that y∈A.Thus A=AΦ. Definition 8We say a tracial subalgebra A of M satisfies L2-density,if A+J(A)is dense in L2(M)in the usual Hilbert space norm on that space. For more detailed information about L2-density,see[13]. Theorem 4Let A be a tracial subalgebra of M and it satisfies L2-density.Then the following conditions are equivalent: (i)A is a subdiagonal subalgebra of M. (ii)For growth functions Φ which satisfy the?2and-conditions,A has LΦ-factorization and AΦis a tracial subalgebra of M. Proof(ii)?(i).It is clear that AΦis a subdiagonal subalgebra of M.Then So we have[A]2=[AΦ]2,[J(A0)]2=[J((AΦ)0)]2.Since AΦis a subdiagonal subalgebra of M,for x∈ L2(M)?1there exist a unitary u ∈ M and asuch that x=ua.This implies A has L2-factorization.By Theorem 2.4 of[13]we know that A is a subdiagonal subalgebra of M.1 Preliminaries
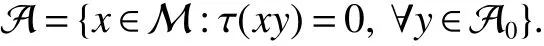
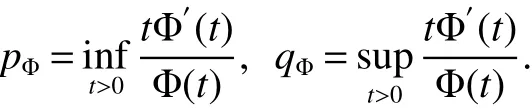
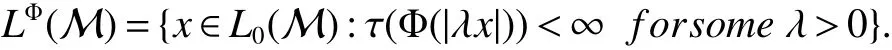
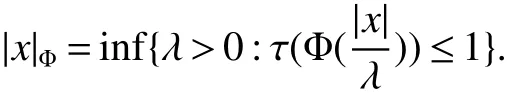
2 Factorization