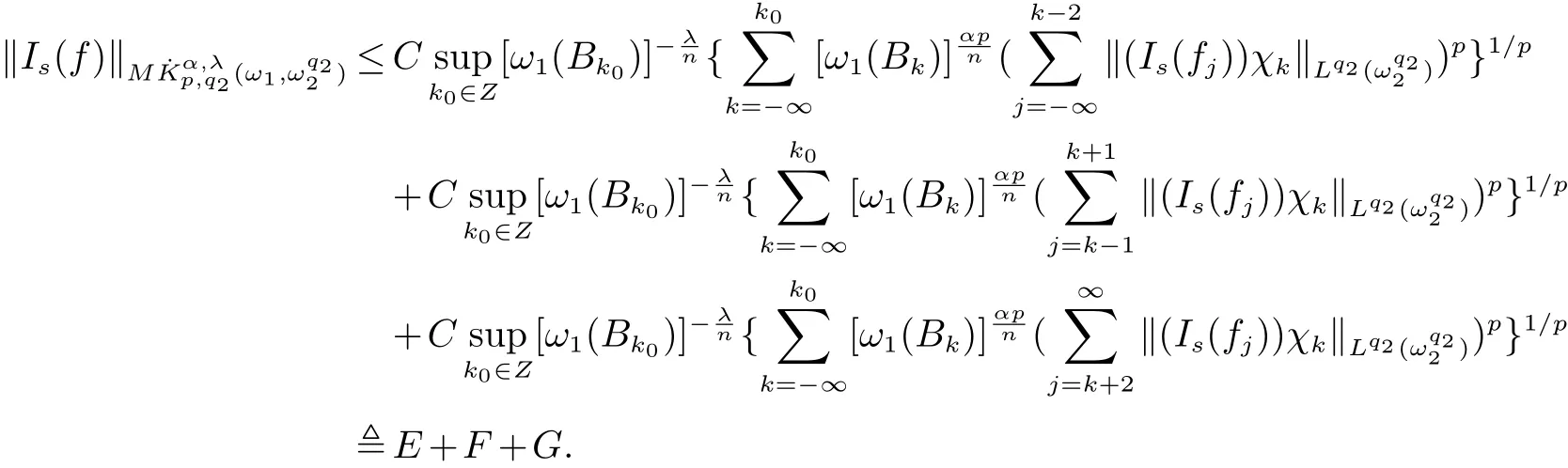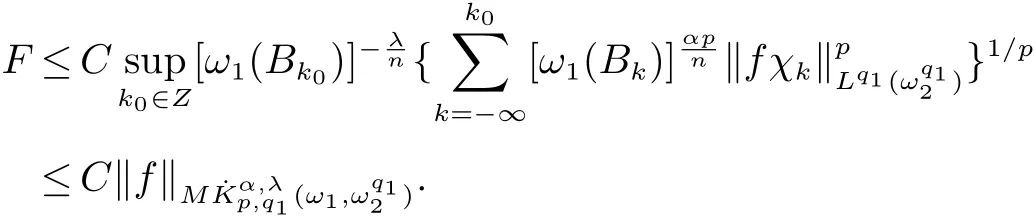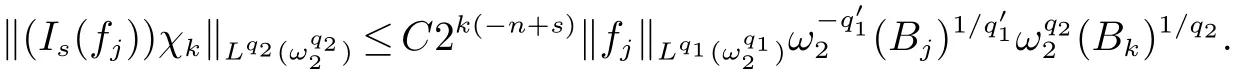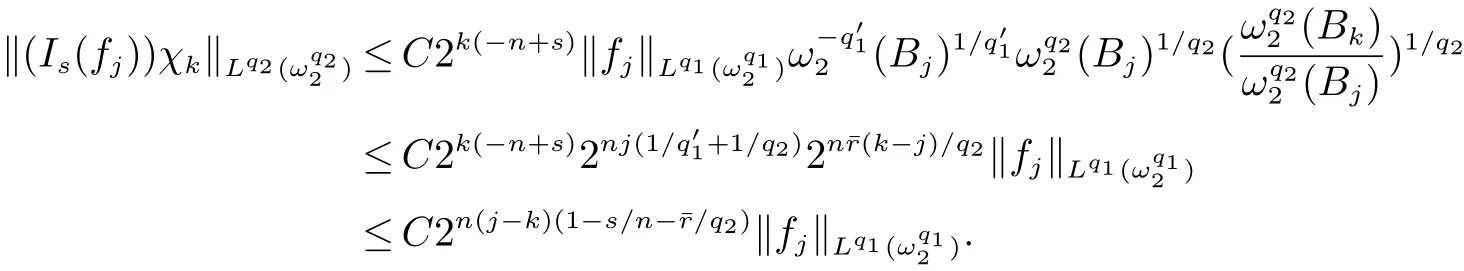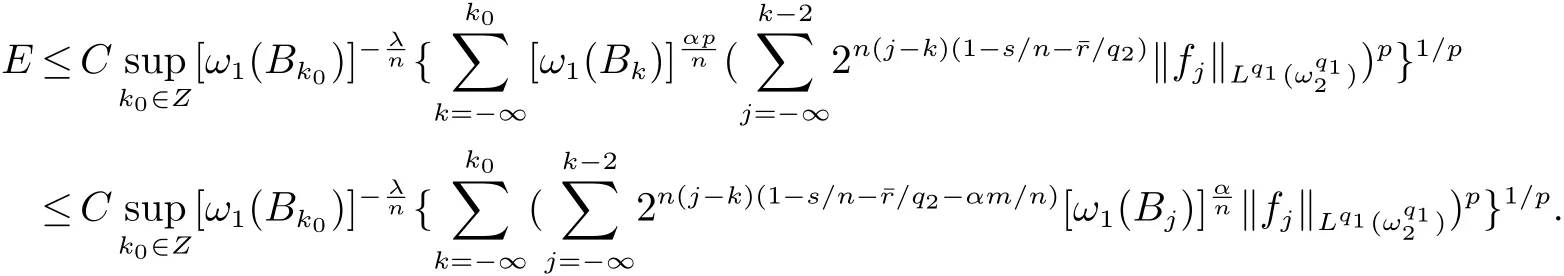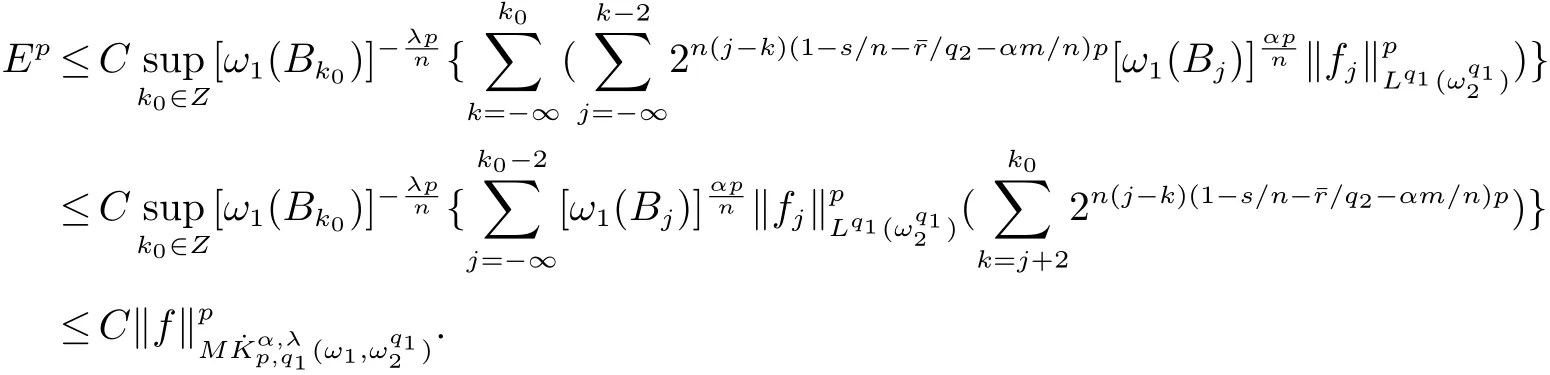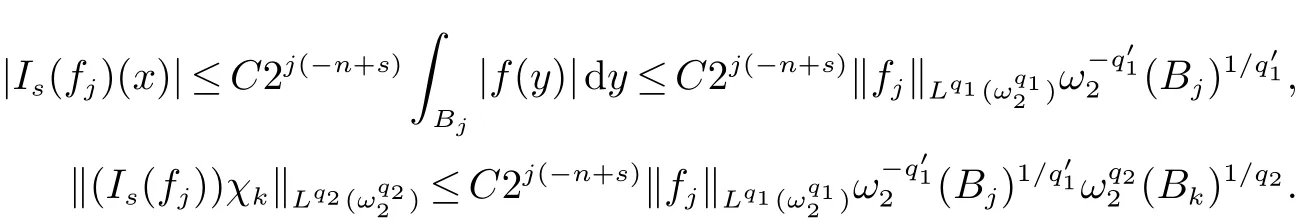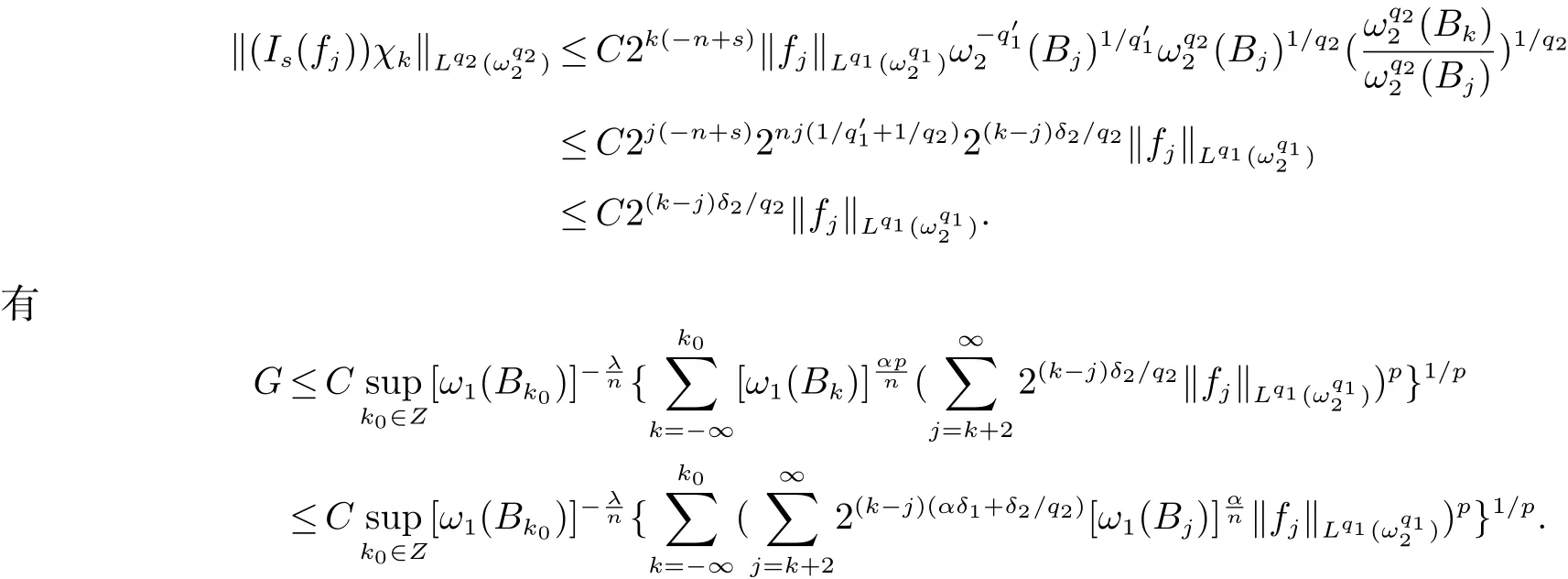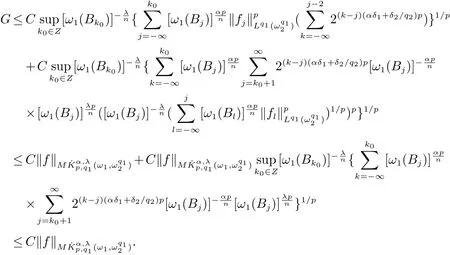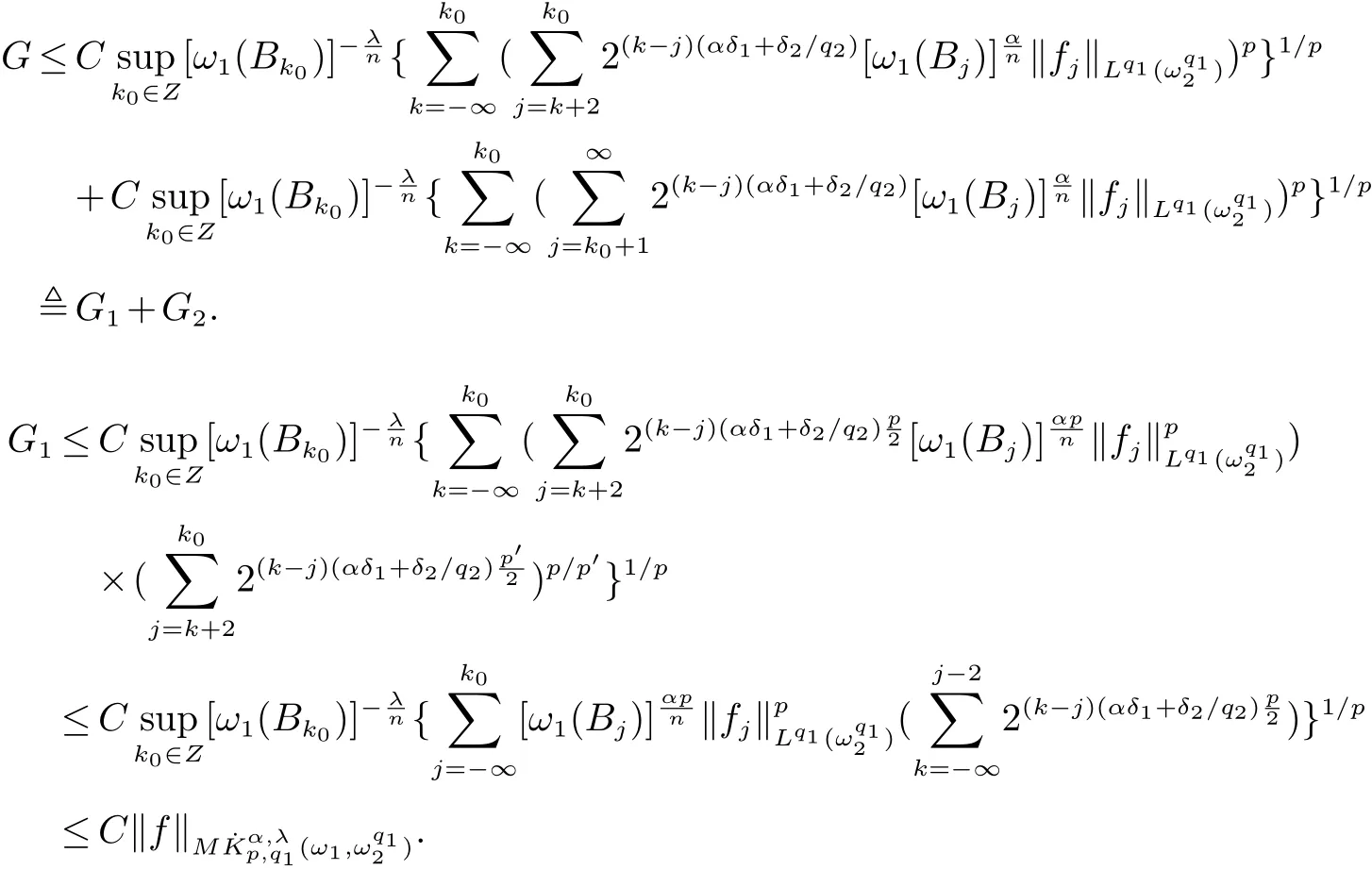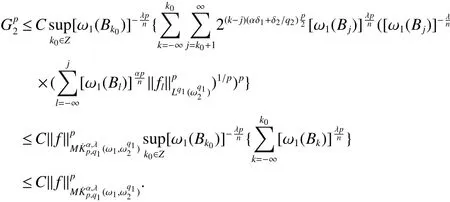分數次積分算子在齊次雙權Morrey-Herz空間上的有界性?
張超楠,周疆,曹勇輝
(新疆大學數學與系統科學學院,新疆烏魯木齊830046)
0 引言
分數次積分算子是研究偏微分方程問題的一類重要算子.為了更好的研究Possion方程,Sobolev[1]引入了經典的分數次積分算子,并證明了Is是(Lp(Rn),Lq(Rn))型的.1995年,Fan Dashan等[2]給出了奇異積分算子在Morrey空間上的有界性.2005年,Lu Shanzhen等[3]在研究奇異積分算子時,引入了一類與PDE相關的,比Herz空間和Morrey空間更一般的齊次Morrey-Herz空間,這類空間很快受到人們的重視,隨后,Morrey-Herz空間上的一些極具研究價值的結果不斷出現.2009年,Yasuo Komori等[5]證明了分數次積分算子在加權Herz空間上的有界性.2010年,Kuang Jichang[6]給出了齊次雙權Morrey-Herz空間的定義,并得出了一類新的積分算子在其上的有界性.受文獻[5]和[6]的啟發,本文研究分數次積分算子在齊次雙權Morrey-Herz空間上的有界性.
1 預備知識
定義1[1]分數次積分算子Is定義如下:
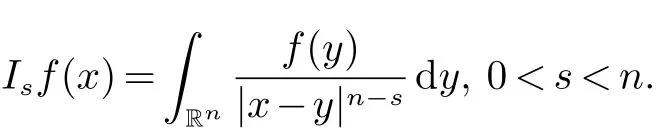
下面給出齊次雙權Morrey-Herz空間的定義:
定義2[6]設α∈R,λ≥0,0 定義3[4]設1 定義4[4]設1 定義5[4]設 δ>0,稱 ω ∈RD(δ),是指 以下引理在本文證明中是必要的: 引理1[4]設1上是有界的. 引理2[5]如果ω∈Ap,則 引理3[5]設1 引理4[5]如果ω∈A(p1,p2),則 定理 1設0≤λ<∞,0 (1)ω1∈Am,ω1∈RD(δ1),1≤m<∞, (3)?δ2/δ1q2<α<(1?s/n?r/q2)n/m, 定理1的證明 首先對F進行估計,由引理1知 從而有 結合引理2及引理4,得 將上述結果應用到E中,有 當1 結合引理3及引理4,得 當0 當1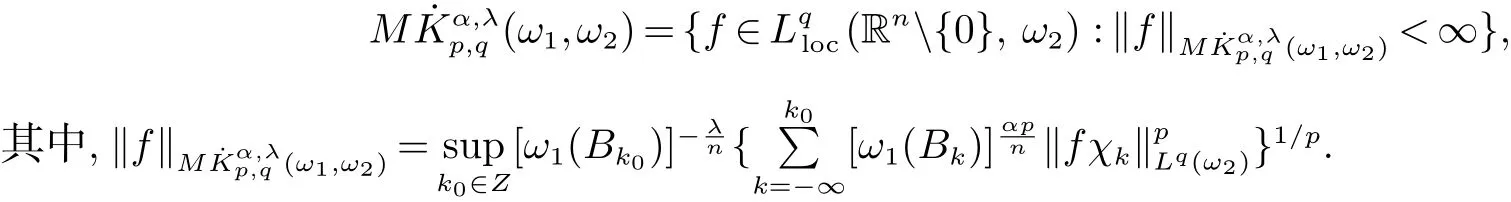
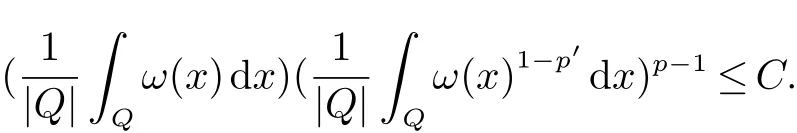
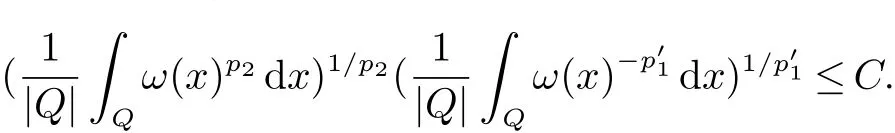
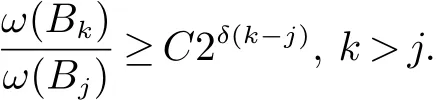

2 主要定理及證明