樹形網(wǎng)絡(luò)的平均介數(shù)*

霍慧鳴，趙海興

（青海師范大學(xué) 計算機學(xué)院，青海 西寧 810008）

自從20世紀(jì)30年代Radcliffe Brown提出社會網(wǎng)絡(luò)分析概念以來，社會網(wǎng)絡(luò)分析已經(jīng)逐步成為一種重要的社會定量研究方法[1]。近年來，隨著計算機技術(shù)和互聯(lián)網(wǎng)的飛速發(fā)展，如何利用文本挖掘、機器學(xué)習(xí)等技術(shù)面向互聯(lián)網(wǎng)進行社會網(wǎng)絡(luò)挖掘和分析成為了一個新的研究課題。隨著數(shù)據(jù)挖掘技術(shù)的進步以及計算機處理能力的提高，研究者們分析的社會網(wǎng)絡(luò)的規(guī)模也急劇增大。這些分析和其他現(xiàn)實網(wǎng)絡(luò)分析一樣，面臨網(wǎng)絡(luò)節(jié)點規(guī)模巨大的挑戰(zhàn)。

現(xiàn)實生活中存在的大量復(fù)雜系統(tǒng)都可以通過不同的網(wǎng)絡(luò)加以描述，網(wǎng)絡(luò)科學(xué)已成為眾多學(xué)科匯聚的交叉點。復(fù)雜網(wǎng)絡(luò)是近幾年科學(xué)研究發(fā)現(xiàn)的一種介于規(guī)則網(wǎng)絡(luò)和隨機網(wǎng)絡(luò)之間的一種更接近于真實網(wǎng)絡(luò)的網(wǎng)絡(luò)模型，錢學(xué)森給出了復(fù)雜網(wǎng)絡(luò)的一個較嚴(yán)格的定義：具有自組織、自相似、吸引子、小世界、無標(biāo)度（無尺度）中部分或全部性質(zhì)的網(wǎng)絡(luò)稱為復(fù)雜網(wǎng)絡(luò)[2]。隨著復(fù)雜網(wǎng)絡(luò)規(guī)模的不斷擴大，對于各個節(jié)點在整個圖中所起作用的研究變得迫切，各個節(jié)點的作用可以用介數(shù)來表示。介數(shù)既能刻畫圖中節(jié)點和邊的重要性，揭示網(wǎng)絡(luò)層次結(jié)構(gòu)，又能用來構(gòu)建基于點介數(shù)或邊介數(shù)的聚類算法，發(fā)現(xiàn)圖中特殊群體，因此，它一直是研究網(wǎng)絡(luò)結(jié)構(gòu)性質(zhì)的一個重要量化手段。首先對于介數(shù)的概念要有一定的了解。在復(fù)雜網(wǎng)絡(luò)研究中，研究者不僅要非常客觀地關(guān)注系統(tǒng)內(nèi)個體之間的相互作用，而且還要注視系統(tǒng)的整體相互作用，表達這種整體相互作用的概念是介數(shù)。介數(shù)是一個全局的變量，反映節(jié)點或邊的作用和影響力，可分為節(jié)點介數(shù)（Vertex Betweenness）和邊介數(shù)（Edge Betweenness）兩種。節(jié)點介數(shù)定義為在網(wǎng)絡(luò)的所有最短路徑中，通過節(jié)點的最短路徑條數(shù)稱之為節(jié)點i的介數(shù)[3]；邊的介數(shù)定義為在網(wǎng)絡(luò)的所有最短徑經(jīng)過邊的介數(shù)；網(wǎng)絡(luò)平均節(jié)點介數(shù)定義為網(wǎng)絡(luò)中所有節(jié)點介數(shù)的平均值；網(wǎng)絡(luò)平均邊介數(shù)指網(wǎng)絡(luò)中所有邊介數(shù)的平均值。節(jié)點的介數(shù)在一定程度反映的是節(jié)點在網(wǎng)絡(luò)中的核心作用，節(jié)點的介數(shù)越大，表明節(jié)點的核心作用越強，刪除這樣的節(jié)點會使大量節(jié)點對之間的最短路徑變長，邊的介數(shù)也有同樣的性質(zhì)。

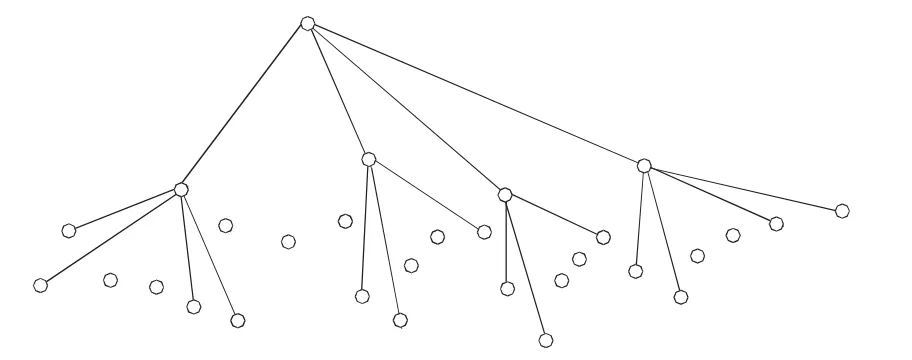
本文主要討論樹形網(wǎng)絡(luò)的平均節(jié)點介數(shù)，其中節(jié)點介數(shù)是經(jīng)過該節(jié)點的所有路徑，網(wǎng)絡(luò)平均節(jié)點介數(shù)是指所有節(jié)點介數(shù)的平均值。下面舉一個具體的例子來分析節(jié)點介數(shù)和邊介數(shù)。圖1所示中各節(jié)點與邊的介數(shù)可以分別表示如下。

圖1 節(jié)點介數(shù)與邊介數(shù)關(guān)系圖

表1中的平均節(jié)點介數(shù)為4.375，平均邊介數(shù)為7.25，依據(jù)Newman[4]提出的介數(shù)新的計算機方法和Brandes算法可以更快地計算出介數(shù)。更多的介紹見參考文獻[5-7]。

表1 各節(jié)點介數(shù)與邊介數(shù)的關(guān)系

本文研究了樹形網(wǎng)絡(luò)中平均節(jié)點介數(shù)最大的圖和最小的圖，所有樹的平均節(jié)點介數(shù)小于路的平均節(jié)點介數(shù)和其大于星形圖的節(jié)點平均介數(shù)。

復(fù)雜網(wǎng)絡(luò)樹形圖中的介數(shù)源于網(wǎng)絡(luò)中對個體重要性的評估，一個節(jié)點介數(shù)表示所有節(jié)點對之間通過該節(jié)點的最短路徑條數(shù)，因此它能夠刻畫節(jié)點在網(wǎng)絡(luò)中的重要程度，任意節(jié)點v的介數(shù)值定義為[8]：

其中，δst為節(jié)點 s 到 t的最短路徑數(shù)目，δst（v）為節(jié)點 s 到t的最短路徑中經(jīng)過節(jié)點v的最短路徑數(shù)目。

樹形網(wǎng)絡(luò)中節(jié)點介數(shù)就是通過該節(jié)點的路徑數(shù)目。如有一個n個節(jié)點的樹形網(wǎng)絡(luò) N，節(jié)點用v表示，平均節(jié)點介數(shù)可表示為：

1 樹形網(wǎng)絡(luò)中最大平均節(jié)點介數(shù)圖

隨著復(fù)雜網(wǎng)絡(luò)規(guī)模的不斷增加，節(jié)點數(shù)目也在不斷地增加，對于一些冗余的節(jié)點刪除變得更加必要，這就需要對于節(jié)點的作用給出一個正確的評估，需要了解哪些圖形具有最大的平均節(jié)點介數(shù)，網(wǎng)絡(luò)結(jié)構(gòu)可以盡可能地向這樣的結(jié)構(gòu)變化。本節(jié)主要介紹具有最大平均節(jié)點介數(shù)的網(wǎng)絡(luò)。

引理 1 如圖 2所示，N1是一棵樹，N1′是經(jīng)過圖 2的變換得到的，則等號成立當(dāng)且僅當(dāng)N1是一條路。

證明 有k個節(jié)點的圖，如圖2所示，圖N1中節(jié)點A上有p個分支，有n個節(jié)點的為分支P1，有m個節(jié)點的為分支P2。圖N1把分支P1添加到分支P2之后得到圖的N1′分支P1+P2。則節(jié)點A上變成了P-1個分支。因為分支節(jié)點介數(shù)與分支結(jié)構(gòu)和總節(jié)點個數(shù)有關(guān)，現(xiàn)在樹形圖 N1和 N1′的平均節(jié)點介數(shù) B（N1）和 B（N1′）中，圖 N1和 N1′中除了節(jié)點 A， 分支 P1、P2及分支 P1+P2的節(jié)點介數(shù)有變化，其他分支對應(yīng)節(jié)點介數(shù)都沒有改變。把其他分支節(jié)點的介數(shù)之和用M表示。

圖2 N1 與 N1′的關(guān)系圖

圖N1上節(jié)點介數(shù)分別表示如下：

表2 分支P1各節(jié)點介數(shù)

表3 分支P2各節(jié)點介數(shù)

平均節(jié)點介數(shù)為：

圖N1′中節(jié)點介數(shù)分別表示如下：

表4 分支P1+P2的介數(shù)

平均節(jié)點介數(shù)可以表示為：

將變化前后的兩個圖的平均介數(shù)進行比較，比較結(jié)果為：

由式（1）知，k≥m+n+1，B（N1）≤B（N1′），等號成立當(dāng)且僅當(dāng) N1是一條路時，故可得 B（N1）≤B（N1′），證畢。

路是各個節(jié)點的度不大于2的連通的無圈圖，兩端的兩個點的度為1，中間的各個節(jié)點的度均為2。n個節(jié)點的路中兩端的兩個節(jié)點為1度的葉子節(jié)點，其介數(shù)為0。假如第 i個節(jié)點的介數(shù)，i的取值范圍是1～n，各個節(jié)點的介數(shù)可以表示為（n-i）（i-1），其平均介數(shù)為：

定理1 路是具有最大平均節(jié)點介數(shù)的樹形圖，n個節(jié)點的平均介數(shù)為：。

證明 用歸納法證明如下。

（1）當(dāng)n=4時，有4個節(jié)點的圖只有兩種形式，即路和星形圖，路的平均節(jié)點介數(shù)為1，星形圖的平均節(jié)點介數(shù)為0.75，路具有較大的平均節(jié)點介數(shù)，成立。

（2）假如對于n

圖3 n

綜上所述，在樹形圖中，路具有最大的平均節(jié)點介數(shù)，證畢。

2 樹形網(wǎng)絡(luò)中具有最小平均節(jié)點介數(shù)的圖

本節(jié)主要研究樹形網(wǎng)絡(luò)的結(jié)構(gòu)中具有最小的平均節(jié)點介數(shù)。對此可以知道哪些結(jié)構(gòu)的網(wǎng)絡(luò)中節(jié)點的相對作用較小，刪除這樣的節(jié)點的分支，對于整個的網(wǎng)絡(luò)影響相對不大。

引理 2 如圖 4所示，N2所示是一棵樹，N2′是由 N2把圖4所示的1度點分支添加到節(jié)點A得來的，則B（N2）≥B（N2′），等式成立當(dāng)且僅當(dāng) N2是一個星形圖。

圖4 樹形網(wǎng)絡(luò)中節(jié)點分析圖

證明 假如對于圖4所示的N2中節(jié)點A有p個分支，k個節(jié)點的圖，圖中有一個m個1度點的分支。圖N2′把圖N2中m個1度的點添加到節(jié)點 A上，分支變成了1度點。節(jié)點A的分支個數(shù)變成了p+m個。圖N2和N2′中的平均節(jié)點介數(shù)用 B（N2）和 B（N2′）表示。 N2和 N2′中m個1度點的介數(shù)仍然為零，沒有改變。其中，除了節(jié)點A、節(jié)點m+1有變化，其他p-1個分支對應(yīng)節(jié)點介數(shù)都沒有改變。未改變的分支節(jié)點介數(shù)和用M表示。

圖N2改變的節(jié)點介數(shù)和為：

圖 N2′的節(jié)點介數(shù)和為：

用 B（N2）減去 B（N2′）等式可得：

由式（3）可知，k≥m+2 時，有 B（N2）≥B（N2′）成立，等號成立當(dāng)且僅當(dāng)是一個星形圖時。其他情況都是k>m+2，故引理可證，證畢。

星形圖是只有一個節(jié)點的度不為1，其他節(jié)點的度都為1的圖。星形圖中，度為1的節(jié)點的介數(shù)都是0，在星形圖中，稱這個有最大度的節(jié)點為Hub節(jié)點，也只有這么一個節(jié)點的介數(shù)不是0。假如有n個節(jié)點的星形圖，其中有n-1個節(jié)點的介數(shù)為0，Hub節(jié)點的介數(shù)為：。故有n個節(jié)點的星形圖的平均節(jié)點介數(shù)為：/n=。

定理2 星形圖具有最小的節(jié)點平均節(jié)點介數(shù)，n個節(jié)點的星形圖的平均節(jié)點介數(shù)為：。

證明 用歸納法證明如下。

（1）當(dāng)n=4時，有4個節(jié)點的圖只有兩種形式，即路和星形圖，路的節(jié)點平均介數(shù)為1，星形圖的節(jié)點平均介數(shù)為0.75，星形圖有最小平均節(jié)點介數(shù)，成立。

（2）假設(shè)當(dāng)n

圖5 樹形網(wǎng)絡(luò)具有最小平均節(jié)點介數(shù)的圖

綜上所述，星形圖具有最小的平均節(jié)點介數(shù)，證畢。

本文主要討論了在復(fù)雜網(wǎng)絡(luò)中樹形網(wǎng)絡(luò)的平均節(jié)點介數(shù)最大和最小的網(wǎng)絡(luò)，對于與之相關(guān)節(jié)點介數(shù)增加和減少給出了兩個引理，節(jié)點介數(shù)是通過該節(jié)點的路徑數(shù)。更多的介數(shù)應(yīng)用和算法分析可以參考文獻[9]～[11]。

[1]SCOT J.Social network analysis： a handbook （2nded）[M].Sage Publications，1991.

[2]張嗣瀛.復(fù)雜系統(tǒng)與復(fù)雜性科學(xué)[EB/OL].http：//news.qdu.edu.cn/newx？ newsid=1514，2006-05-05.

[3]張曉林，袁莉，楊峰，等.基于 Web的個性化信息服務(wù)機制[J].現(xiàn)代圖書情報技術(shù)，2001（1）：25-29.

[4]NEWMAN M E J.Scientific collaboration networks.II.shortest paths， weighted networks， and centrality[J].Phys.Rev.E， 2001， 64（1）.

[5]LEWIS T G.網(wǎng)絡(luò)科學(xué)原理與應(yīng)用[M].陳向陽，巨修紅練，譯.北京：機械工業(yè)出版社，2011.

[6]馬杰良，邢雪，安莉莉.基于科研合作網(wǎng)絡(luò)的節(jié)點樞紐特性研究[J].東北電力大學(xué)學(xué)報，2008，28（2）：72-76.

[7]Zhang Z Z， Zhou S G， Y Qi， et al.Topologies and laplacian spectra of a deterministic uniform recursive tree[J].Eur， Phys， J.B， 2008（63）：507-513.

[8]唐晉韜，王挺.復(fù)雜社會網(wǎng)絡(luò)的介數(shù)性質(zhì)近似計算方法研究[J].計算機工程與科學(xué)，2008，30（12）：9-14.

[9]王小光，王鋒，李森.基于介數(shù)影響矩陣的通信網(wǎng)絡(luò)節(jié)點重要度評價方法[J].空軍工程大學(xué)學(xué)報，2012，13（5）：80-84.

[10]何宇，趙洪利，姚曜，等.介數(shù)中心性和平均最短路徑長度整合近似算法[J].復(fù)雜系統(tǒng)與復(fù)雜性科學(xué)，2011，8（3）：44-53.

[11]賈煒，馮登國，連一峰.基于網(wǎng)絡(luò)中心性的計算機網(wǎng)絡(luò)脆弱性評估方法[J].中國科學(xué)院研究生學(xué)報，2012，29（4）：529-535.