蛋白質序列的混合特征值對折疊速率的影響

李欣穎，白鳳蘭

(大連交通大學理學院，遼寧 大連116028)

1 材料和方法

1.1 數據

本文從文獻［15－18］中選取了83個蛋白質，氨基酸序列從PDB庫取得［19］。在選取44個蛋白質中包括13個全α類蛋白質，18個全β類蛋白質和13個混合類蛋白質，以及39個未分類蛋白質。

1.2 蛋白質編碼序列的特征值提取

氨基酸的標準化屬性Pnorm(i)的計算公式為:

其中，Pnorm(i)是氨基酸的標準化屬性，P(i)是氨基酸序列中第i個殘基的屬性，Pmax和Pmin分別表示氨基酸屬性中的最大值和最小值。

蛋白質序列中氨基酸的平均屬性Pave的計算公式:

其中，Pave是蛋白質的氨基酸平均屬性，P(j)是氨基酸序列中第j個殘基的屬性，N是氨基酸序列的殘基數。

蛋白質序列的復雜度LZc計算公式:

蒙牛在2012年的經營活動中發現到自己在乳制品方面最大的短板就是嬰幼兒奶粉，在2012年中國嬰幼兒奶粉的市場里，雅士利排第七名，在2012年雅士利擁有5.8%的市場份額，嬰幼兒奶粉產品發展已經非常成熟，擁有成熟的技術、產品和市場，蒙牛在擴大自己經營規模的時候，打開了自己在奶粉產品的市場，基本上把自己的缺陷彌補了，同時蒙牛又可以彌補雅士利在企業管理上的不足。蒙牛與雅士利的合并控股是一個雙贏的局面，整體的價值都得到了提升。

其中，S表示的是序列，c(S)是序列S的復雜度［11］。

20 個氨基酸 αc、Cα、K0、Pβ、Ra、ΔASA、PI、ΔGhD、Nm、Mu、El屬性利用公式(1)計算出標準化后的值。

其中，αc是 α 螺旋的 C 端動力［20－21］，Cα是 α螺旋接觸面積［15］，K0是可壓縮性［22－23］，Pβ是 β 折疊趨勢［21］，Ra是在溶劑中的收縮率［24］，ΔASA 是溶劑可及表面積［25］，PI(at 25℃)表示氨基酸的等電點［26］，ΔGhD是吉布斯自由能變性蛋白水化的變化Nm是平均中程接觸，Mu是折射率，EL是長距離的非鍵能［15］。

利用20個氨基酸標準化后的值和公式(2)、(3)計算了13個全α類蛋白質，18個全β類蛋白質和 13 個混合類蛋白質 αc、Cα、K0、Pβ、Ra、ΔASA、PI、ΔGhD、Nm、LZc、Mu、EL 的特征值，以及 39 個蛋白質的 K0、Rα、ΔASA、Mu、El的特征值，由于數據多沒列在文章里。

2 結果與討論

首先，利用多元線性回歸函數分別計算了13個全α類蛋白質、18個全β類蛋白質、13個混合類蛋白質和未分類的39個蛋白質的12種特征值與折疊速率之間的相關性，實驗值與預測值之間的相關系數分別達到了 0.99、0.96、0.99、0.865，但是用 Jackknife方法檢驗，都得出p＞0.05。由此可知，12種特征值當中某些特征值對蛋白質的折疊速率沒有影響，這樣經過多次試驗，對于全α類蛋白質選取有效特征值Cα、Ra、LZc，對于全 β 類蛋白質選取有效特征值 K0、Pβ、Ra、ΔASA、Nm，對于混合類蛋白質選取有效特征值K0、ΔASA、PI，對于未分類的蛋白質選取有效特征值 K0、Rα、ΔASA、Mu、El，計算這些特征值與折疊速率ln(kf)之間的相關性。

其次，分別對全α類蛋白質、全β類蛋白質、混合類蛋白質和未分類的蛋白質的有效特征值與折疊速率做相關性分析，并與其它方法進行比較。

選取13個全α類蛋白質Cα、Ra、LZc3個特征值與折疊速率ln(kf)做回歸方程:

用p值檢驗了方程(4)每一項特征值，每一特征值對應的p值都小于0.05。實驗值與預測值之間的相關系數R=0.89。用Jack-knife方法檢驗，得出R=0.77、t=4.04、p ＜0.05。

Gromiha文章中選取了6個全α類蛋白質的1個特征值αc作線性回歸，本文在6個數據的基礎上增加到13個全α類蛋白質，用特征值αc作線性回歸，得到回歸方程:

本文用p值檢驗了得到的方程(5)，p＞0.05。實驗值與預測值之間的相關系數R=0.03，t=－0.097。在選取13個全α類蛋白質的Cα、Ra、LZc3個特征值中，得到回歸方程的相關系數為0.89，說明選取的特征值Cα、Ra、LZc對全α類蛋白質有影響。對比結果見表1。

表1 全α類蛋白質回歸分析結果Table 1 The results of all-α proteins regression analysis

選取 18 個全 β 類蛋白質的 K0、Pβ、Ra、ΔASA、Nm5個特征值與折疊速率ln(kf)做回歸方程:

用p值檢驗了以上方程的每一項特征值，每一特征值對應的p值都小于0.05。實驗值與預測值之間的相關系數R=0.93。用Jack-knife方法檢驗，得出 R=0.78、t=4.93、p ＜0.001。

同樣18個全β類蛋白質，選取Gromiha文章中的 K0、Pβ、Ra、ΔASA4 個特征值作線性回歸，得到方程:

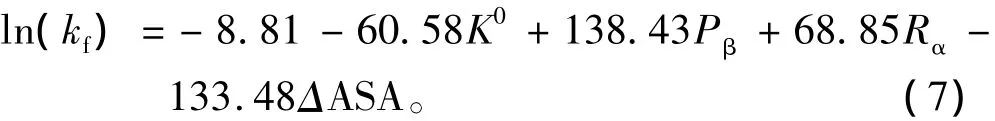
用p值檢驗了以上方程的每一項特征值，其對應的p值都小于0.05。實驗值與預測值之間的相關系數R=0.89。用Jack-knife方法檢驗，得出R=0.73、t=4.28、p ＜ 0.001。這說明本文選取的特征值 K0、Pβ、Ra、ΔASA、Nm對全 β 類蛋白質有影響。對比結果見表2.

表2 全β類蛋白質回歸分析結果Table 2 The results of all－β proteins regression analysis

選取13個混合類蛋白質 K0、ΔASA、PI三個特征值與折疊速率ln(kf)做回歸方程:

用p值檢驗了以上方程的每一項特征值，每一特征值對應的p值都小于0.05。實驗值與預測值之間的相關系數R=0.98。用Jack-knife方法檢驗，得出R=0.97、t=13.46、p ＜0.001。

同樣的13個混合類蛋白質，選取Gromiha文章中的 K0、Ra、ΔASA、ΔGhD4 個特征值作線性回歸，得到方程:

用p值檢驗了以上方程的每一項特征值，每一特征值對應的p值都小于0.05。實驗值與預測值之間的相關系數R=0.96。用Jack-knife方法檢驗，得出 R=0.91、t=7.07、p ＜0.001。這說明本文選取的特征值K0、ΔASA、PI對混合類蛋白質有影響。對比結果見表3。

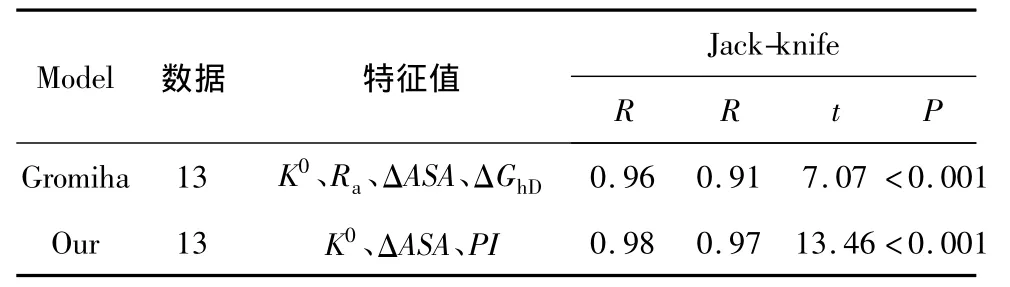
表3 混合類蛋白質回歸分析結果Table 3 The results of mixed class proteins regression analysis

對于未分類的39個蛋白質，選取5個特征值K0、Rα、ΔASA、Mu、El與折疊速率 ln(kf)作回歸方程:

用p值檢驗了以上方程的每一項特征值，每一特征值對應的p值都小于0.05。實驗值與預測值之間的相關系數R=0.86，用 Jack-knife 方法檢驗，得出 R=0.81、t=8.32、p＜0.001。

同樣的39個未分類蛋白質，選取Gromiha文章中的K0、Ra、ΔASA、ΔGhD4 個特征值作線性回歸，得到方程:

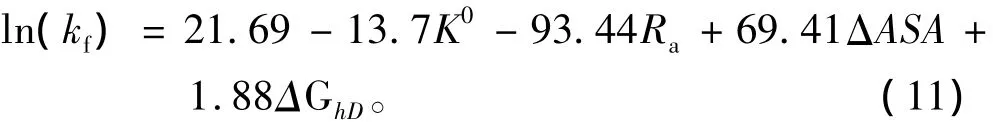
用p值檢驗了以上方程的每一項特征值，其對應的p值都大于0.05。實驗值與預測值之間的相關系數R=0.697。用 Jack-knife 方法檢驗，得出 R=0.48、t=3.37、p ＞ 0.001。這說明選取的特征值 K0、Rα、ΔASA、Mu、El對未分類蛋白質有影響。對比結果見表4。

表4 未分類蛋白質回歸分析結果Table 4 The results of unclassified proteins regression analysis

通過實驗計算得出，對于未分類蛋白質選取5個特征值 K0、Rα、ΔASA、Mu、El計算蛋白質折疊速率預測值，與ln(kf)有良好的相關性。

對于不同類別的蛋白質，其折疊速率有很大的區別。本文研究不同的特征值對不同類別的蛋白質折疊速率的影響，以及特征值對未分類蛋白質折疊速率的影響。從本文的實驗結果發現，Cα、Ra、LZc3個特征值對全α類蛋白質折疊有一定的影響，對于全β類蛋白質，在Gromiha文章選取的4個特征值基礎上增加了Nm特征值，使得全β類蛋白質的折疊速率有所提高，相關系數達到0.93。為了說明Nm特征值對全β類蛋白質的折疊速率有影響，本文又選取了13個數據進行驗證。由實驗結果可知，在增加Nm特征值后全β類蛋白質的折疊速率確實有所提高(見表2)。由此可見，增加的特征值是有效特征值。對于混合類蛋白質，本文選取了3個特征值K0、ΔASA、PI其相關系數比Gromiha文章選取特征值得到的相關系數要高(見表3)。由研究結果發現，特征值K0、ΔASA對全β類蛋白質和混合類蛋白質的折疊速率都有影響。選取 K0、Rα、ΔASA、Mu、El5個特征值對未分類的蛋白質的折疊有一定的影響。

3 結論

蛋白質在生物體內占有重要的地位，是一個生物大分子，由20個氨基酸以肽鍵的形式形成肽鏈。肽鏈在空間結構中通過卷曲形成特定的空間結構，如二級結構和三級結構。氨基酸殘基及周圍介質之間的相互作用決定了蛋白質的結構和折疊速率。由于蛋白質折疊速率對蛋白質功能有一定的影響，近些年來，已有很多方法來預測蛋白質折疊速率。有很多研究工作者從蛋白質的二級結構和三級結構來進行預測蛋白質的折疊速率，但是由于蛋白質的二級結構和三級結構影響因子單一，結構復雜，因此越來越多的研究工作者們開始從蛋白質的一級結構來預測蛋白質的折疊速率。本文就是研究蛋白質的一級結構信息對蛋白質折疊速率的影響，運用生物統計學和生物信息學的方法，選取了蛋白質編碼序列的一些特征值，通過實驗驗證了這些特征值對不同類別的蛋白質折疊速率的影響不同。

本文對于全α類蛋白質，全β類蛋白質，混合類蛋白質和未分類蛋白質分別得到4個線性回歸方程。利用這些回歸方程研究了所選取的特征值與蛋白質折疊速率之間的相關性，得到了較好的結果，比Gromiha文章選取的特征值相關系數都有所提高。不同的數據集對結果有一定的影響，如何減少數據集對結果的影響會在后續工作中進行更深入研究。

References)

［1］ GUO Jianxiu，MA Binguang，ZHANG Hongyu.Progress in protein folding rate prediction［J］，Acta Biophysica Sinica，2006，22(2):89 －95.郭建秀，馬彬廣，張紅雨.蛋白質折疊速率預測研究進展［J］，生物物理學報，2006，22(2):89－95.

［2］ GROMIHA M M，SELVARAJ S.Bioinformatics approaches for understanding and predicting protein folding rates［J］.Current Bioinformatics，2008，3(1):1－9.

［3］ PLAXCO K W，SIMONS K T，BAKER D.Contact order，transition state placement and the refolding rates of single domain proteins［J］.Journal of Molecular Biology，1998，277(4):985－944.

［4］ ZHOU H，ZHOU Y.Folding rate prediction using total contact distance［J］.Biophysical Journal，2002，829(1)，458－463.

［5］ GONG H，ISOM D G，SRINIVASAN R，et al.Local secondary structure content predicts folding rates for simple two-state proteins［J］.J Mol Biol，2003，327(5):1149－1154.

［6］ IVANKOV D N，FINKELSTEIN A V.Prediction of protein folding rates from the amino acid sequence-predicted secondary structure［J］.Proc Nat Acad Sci USA，2004，101(24):8942－8944.

［7］ SHAO H，PENG Y，ZENG Z H.A simple parameter relating sequences with folding rates of small helical proteins［J］.Protein Pept Lett，2003，10(3):277 －280.

［8］ GALZITSKAYA O V，GARBUZYNSKIY S O，IVANKOV D N，et al.Chain length is the main determinant of the folding rate for proteins with three-state folding kinetics［J］.Proteins，2003，51(2):162 －166.

［9］ 徐宏睿，馬彬廣.蛋白質折疊速率決定因素與預測方法的研究進展［J］，生物物理學報，2013，29(3):192－202.XU Hongrui，MA Binguang.Progress in the study on determinants of protein folding rate and method of folding rate prediction［J］.Acta Biophysica Sinica，2013，29(3):192－202.

［10］ MA B G，GUO J X，ZHANG H Y.Direct correlation between proteins'folding rates and their amino acid compositions:an ab initio folding rate prediction［J］.Proteins，2006，65(2):362 －372.

［11］ HUANG J T，XING D J，HUANG W.Relationship between protein folding kinetics and amino acid properties［J］.Amino Acids，2012，43:567 －572.

［12］ GROMIHAM M，THANGAKANI A M，SELVARAJ S.FOLD-RATE:prediction of protein folding rates from amino acid sequence［J］.Nucleic Acids Res，2006，34(suppl_2):70－74.

［13］ HUANG L T，GROMIHA M M.Analysis and prediction of protein folding rates using quadratic response surface models［J］.J Comput Chem，2008，29(10):1675 －1683.

［14］ GOU J X，RAO N N，LIU G X，et al.Predicting protein folding rate from amino acid sequence［J］.Prog Biochem Biophys，2011，37(12):1331 －1338.

［15］ GROMIHA M M.A statistical model for predicting protein folding rates from amino acid sequence with structural class information［J］.Chem Inf Model，2005，45(2):494－501.

［16］于志芬，李瑞芳.同義密碼子的使用偏好性對蛋白質折疊速率的影響［J］，生物物理學報，2013，29(8):603－613.YU Zhifen，LI Ruifang.The influence of synonymous codon bias on protein folding rates［J］.Acta Biophysica Sinica，2013，29(8):603 －613.

［17］胡睿，史小紅，李晉惠.基于序列疏水值震蕩的折疊速率預測［J］.生物信息學，2013，11(2):86 －89.HU Rui，SHI Xiaohong，LI Jinhui.Prediction of protein folding-rate based on the hydrophobic value vibration［J］.Chinese Journal of Bioinformatics，2013，11(2):86 －89.

［18］胡睿，史小紅，基于殘基接觸數的蛋白質折疊速率預測［J］.西安工業大學學報，2013，33(2):146 －150.HU Rui，SHI Xiaohong.Prediction of protein folding-rate based on the residues contact numbei［J］.Journal of Xi’an Technological University，2013，33(2):146 －150.

［19］ BEMAN H M，WESTBROOK J，FENG Z，et al.The protein Databank［J］.Nucleic Acids Res，2000，28(1):235－242.

［20］GROMIHA M M，SARAI O A.Important amino acid properties for enhanced thermostability from mesospheric to hemophilic protein［J］.Biophys Chem，1999，82:51 －67.

［21］ CHOU P Y，FASMAN G D.Prediction of the secondary structure of proteins from their amino acid sequence［J］.Adv Enzym，1978，47:45 －148.

［22］ IQBAL M，VERRALL R E.Implications of protein folding.Additivity schemes for volumes and compressibilities［J］.Biol Chem，1988，263(9):4159 －4165.

［23］GEKKO K，NOGUCHI H.Compressibility of globular proteins in water at 25 degree C［J］.Phys Chem，1979，83(21):2706－2714.

［24］ PONNUSWAMY P K，PRABHAKARAN M，MANAVALAN P.Hydrophobic packing and spatial arrangement of amino acid residues in globular proteins［J］.Biochim Biophys Acta，1980，623(2):301 －316.

［25］ OOBATAKE M，OOI T.Hydration and heat stability effects on protein unfolding［J］.Prog Biophys Mol Biol，1993，59(3):237 －284.

［26］李丹，基于蛋白質圖形表示的膜蛋白跨膜區預測［D］.杭州:浙江理工大學，2012.LI Dan.The prediction oftransmembrane domains based on the graphical representation of protein sequences［D］.HANG zhou:Zhejiang Sci-Tech University，2012.