一類四階奇異非線性積分邊值問題正解的存在性

王全義，鄒黃輝

（華僑大學 數學科學學院，福建 泉州362021）

1 預備知識

兩端簡單支撐的彎曲彈性梁的平行狀態可用四階兩點邊值問題

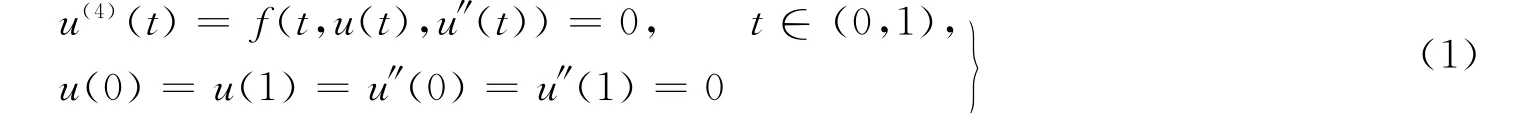
來描述［1］，關于這類邊值問題的正解存在性已受到廣泛的研究［2－5］，微分方程的積分邊值問題在熱傳導、等離子物理、化學工程、流體力學等方面具有廣泛的應用背景.因此，微分方程的積分邊值問題受到許多學者的廣泛關注［6－10］.本文將研究四階奇異非線性積分邊值問題

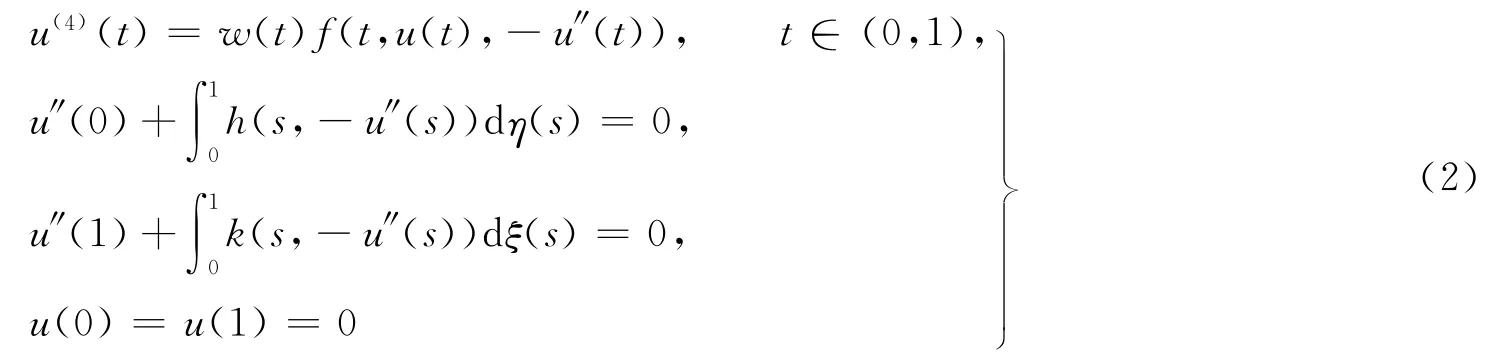
的正解的存在性.式（2）中：f∈C（［0，1］×［0，＋∞）×［0，＋∞），（－∞，＋∞））；h，k∈C（［0，1］×［0，＋∞），［0，＋∞））；w∈C（（0，1），［0，＋∞））；ξ（s）和η（s）在［0，1］上是非減的；在邊值條件（2）中的積分是Riemann－Stieljes積分.

顯然，非線性項f（t，u，p）是可變號的，且w（t）在t＝0，1可能是奇異的.此外，當ξ（s）≡0，η（s）≡0，w（t）≡1時，邊值問題（2）退化為問題（1）.對于具非線性積分邊界條件的四階非線性微分方程的邊值問題（2）的正解存在性問題很少有人研究過.

假設下面的條件成立：

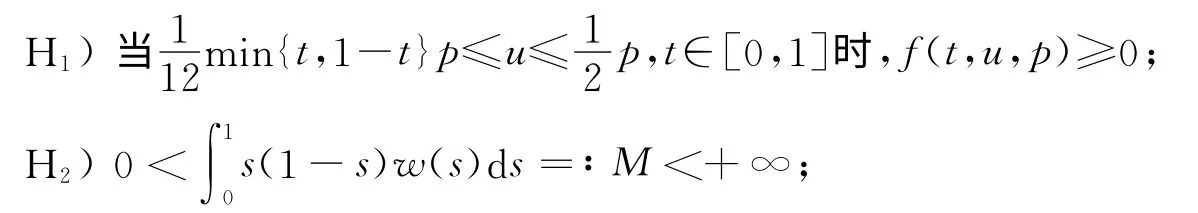
H′1）設f∈C（［0，1］×［0，＋∞）×（0，＋∞］，（－∞，＋∞）），且當［0，1］時，f（t，u，p）≥0.

2 一些引理

設X是Banach空間，K?X非空，且滿足

1）對任意u，v≥0，任意x，y∈K，有ux＋vy∈K；

2）若x∈K，－x∈K，則x＝0，那么稱K為X中的一個錐.

記空間E＝C2［0，1］，在E中定義范數，則E在范數‖x‖下成為一個Banach空間.在E中定義一個錐K，記Kr＝｛x∈K∶‖x‖≤r｝，?Kr＝｛x∈K∶‖x‖＝r｝，＝｛x∈K∶r≤‖x‖≤R｝，其中：0＜r＜R.

引理1［11］設X是Banach空間，P是X中的一個錐，Ω1和Ω2是X中的開集，0∈Ω1，?Ω2，T∶P∩／Ω1→P是全連續算子，如果下列條件之一滿足，即

1）若x∈P∩?Ω1，則‖Tx‖≤‖x‖；若x∈P∩?Ω2，則‖Tx‖≥‖x‖；

2）若x∈P∩?Ω1，則‖Tx‖≥‖x‖；若x∈P∩?Ω2，則‖Tx‖≤‖x‖.那么算子T在P∩（ˉΩ2／Ω1）中有不動點.

引理2函數G（t，s）定義為

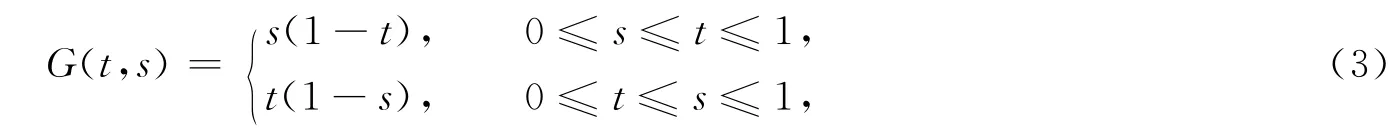
那么，當t，s∈［0，1］時，有

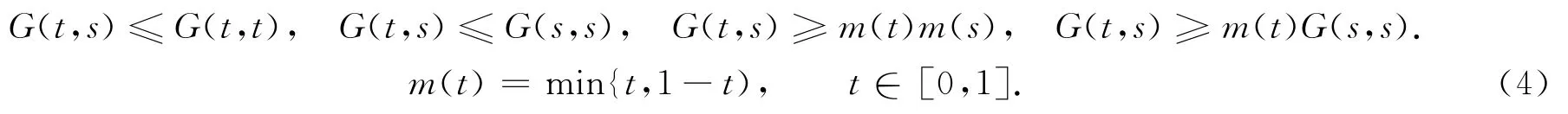
引理3假設條件H1），H2）成立，若如下的邊值問題

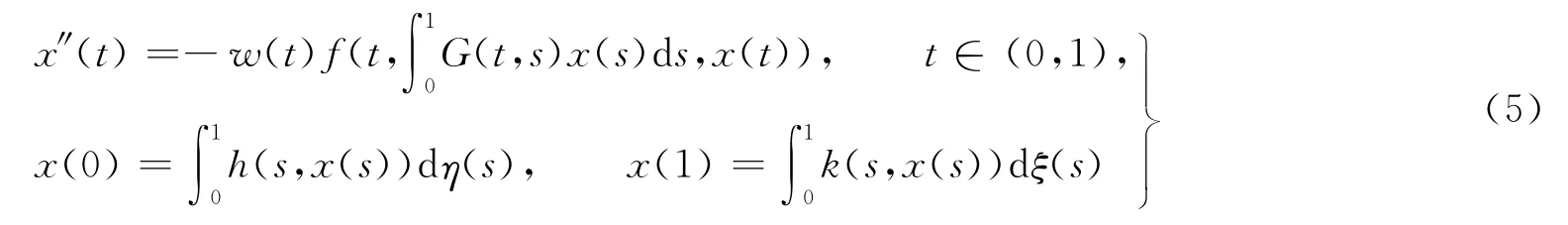
有一個正解x（t），x（t）≥min｛t，1－t｝‖x‖，t∈［0，1］，G（t，s）由式（3）定義，那么積分邊值問題（2）至少有一個正解u（t），且

引理4假設條件H1），H2）成立，如果的積分方程

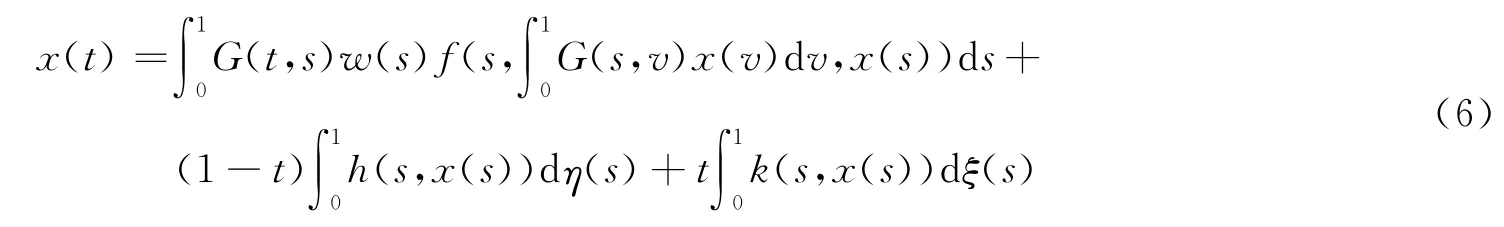
有一個正解x＝x（t），G（t，s）由式（3）定義，那么x＝x（t）是邊值問題（5）的一個正解.

為了應用引理1，錐定義為

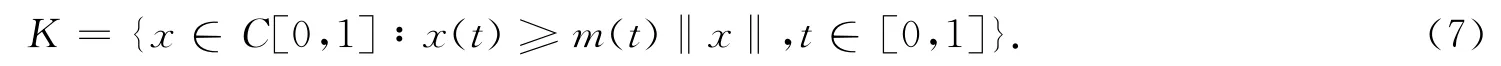
m（t）由式（4）給出.算子T∶K→C［0，1］定義為

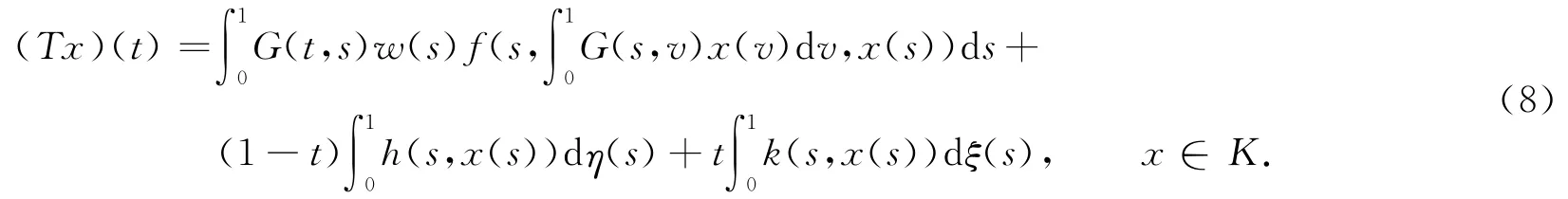
引理5假設條件H1），H2）成立，那么T（K）?K，而且T∶K→K是全連續的.

3 正解的存在性

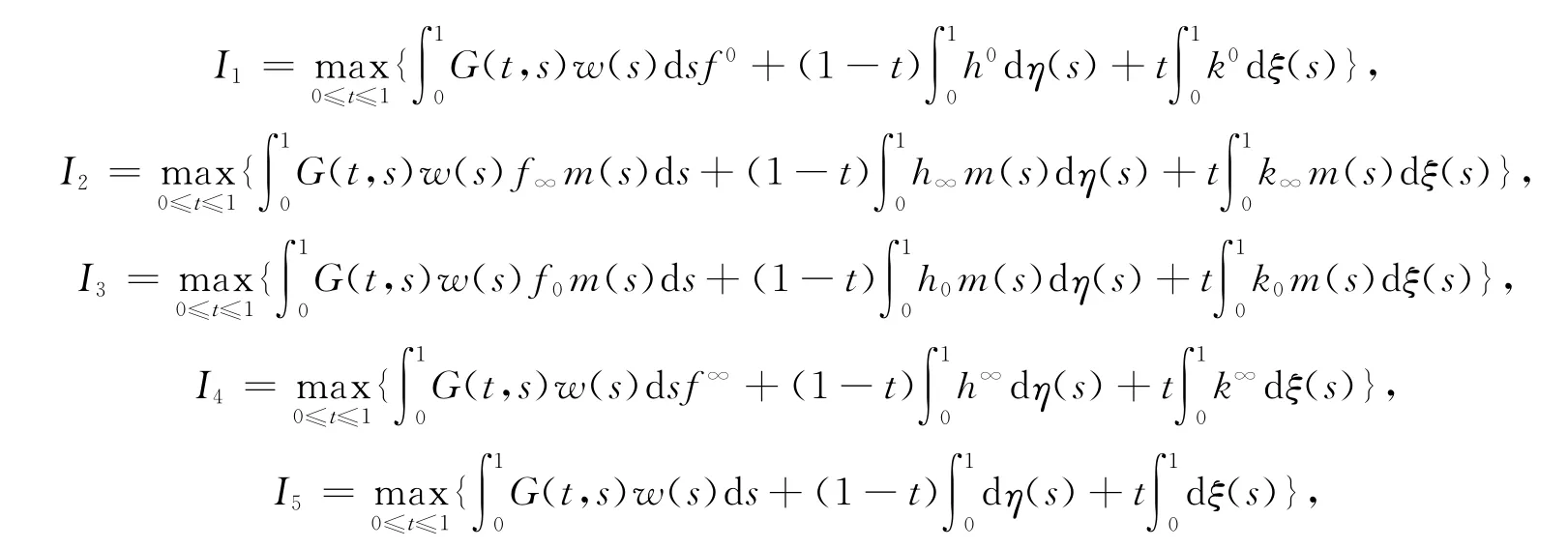
G（t，s）和m（t）分別由式（3），式（4）給出.

如果條件H2）成立，顯然I5是有界的，且0＜I5≤M＋M0，其中

定理1假設條件H1），H2）成立，如果f∞≥0，I1＜1＜I2，則邊值問題（2）至少有一個正解.

證明 考慮式（8）定義的算子T∶K→C［0，1］，由引理5可知T∶K→K是全連續的.又因為I1＜1，0＜I5≤M＋M0，因此存在ε1＞0，使得I1＋ε1I5＜1.對此ε1＞0，存在r1＞0，使得當t∈［0，1］，0＜p≤r1，2u≤p時，就有

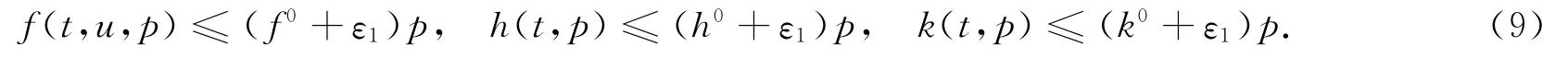
那么由式（6）～式（9），當t∈［0，1］，t∈?Kr1時，可得

故有

因為I2＞1，m（0）＝m（1）＝0，故存在ε2＞0，0＜δ＜1／2，使得

對ε2＞0，存在r22＞0，使得當t∈［0，1］，0≤2u≤p，p≥r22時，有

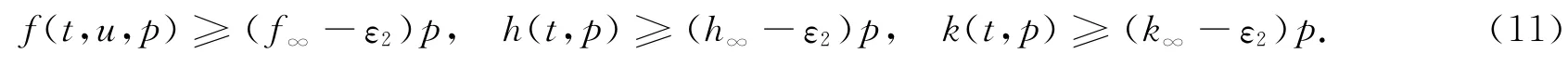
取r2＝max｛r1＋1，δ－1r22｝，所以當t∈［δ，1－δ］，x∈?Kr2時，有

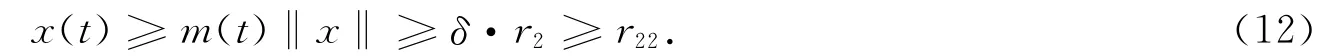
于是當x∈?Kr2，t∈［0，1］時，由式（7），（11），（12）可得

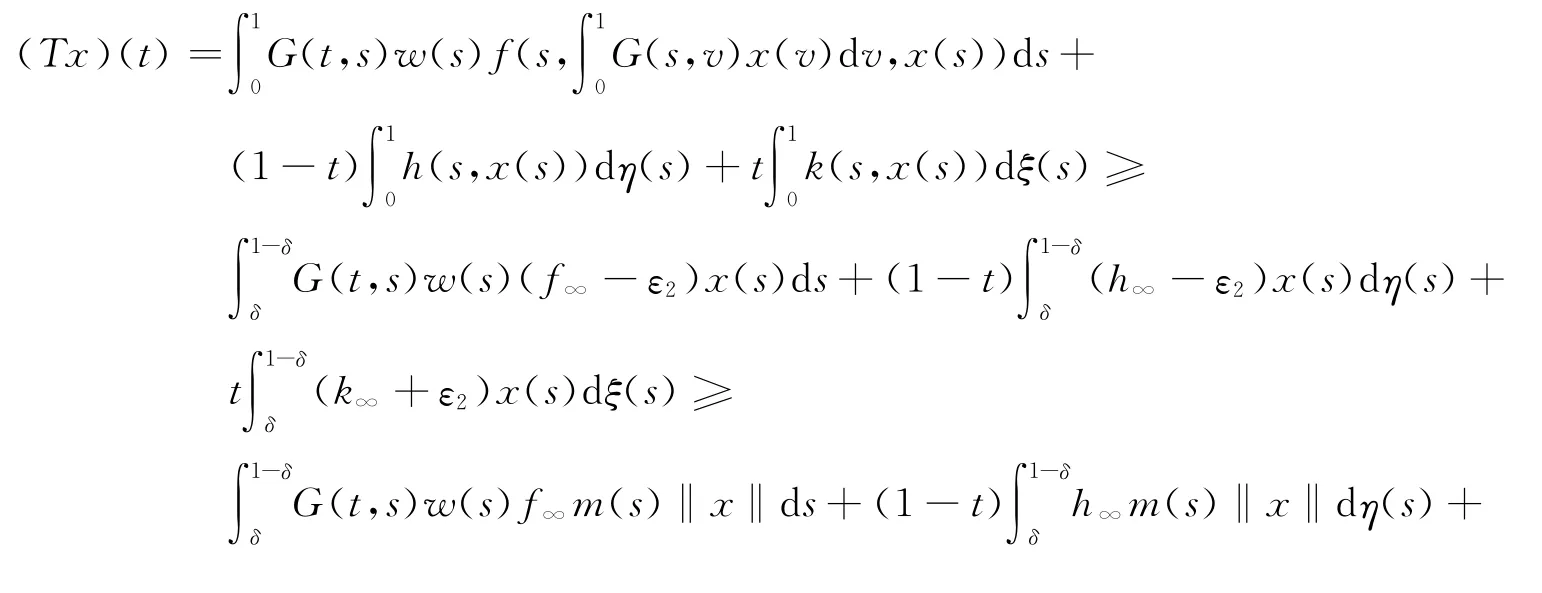
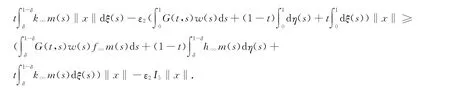
故有

由引理4，式（10），（13）知算子T∶K∩（／Kr1）→K滿足引理1中的所有條件.因此由引理1知有一個不動點x0∈ˉKr1，r2，r1≤‖x0‖≤r2，且x0（t）≥min｛t，1－t｝‖x0‖，t∈［0，1］.由式（8），引理3，4知邊值問題（2）至少有一個正解u0，且，u0（t）≥min｛t，1－t｝‖u0‖，t∈［0，1］.定理1證畢.

在定理1的證明中，假設1＜I2＜＋∞.但是對于I2＝＋∞，容易證明定理1也是成立的.

定理2假設條件H1），H2）成立，如果f∞，f0≥0，I4＜1＜I3，則邊值問題（2）至少有一個正解.

在定理2中假設1＜I3＜＋∞，但是當I3＝＋∞時，容易證明定理2的證明也是成立的.

假設以下條件成立：

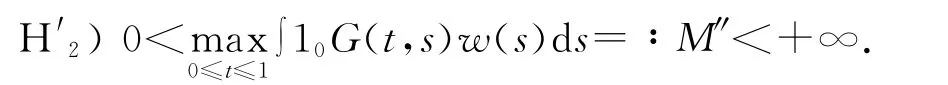
由引理2得，條件H2），H′2）是等價的.

定理3設條件H1），H′2）成立，而且假設存在4個常數ρ1，ρ2，δ，λ，且ρ1＞0，ρ2＞0，ρ1≠ρ2，0＜δ＜1／2，0≤λ＜1使得條件H3）為

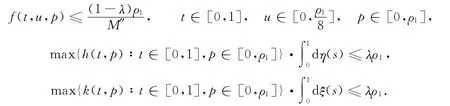
條件H4）為

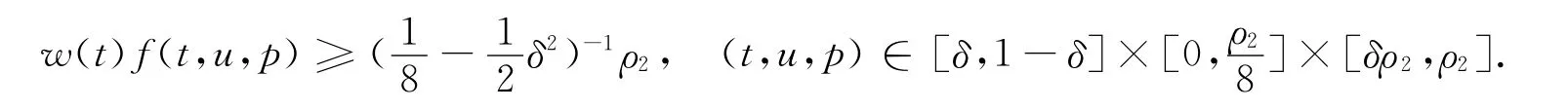
那么積分邊值問題（2）至少有一個正解u，使得在ρ2和ρ2之間.

因為當h（t，p）≡0，k（t，p）≡0，ξ（s）≡0，η（s）≡0，w（t）≡1，邊值問題（2）退化為邊值問題（1）.這時在定理3中，，并且如果取λ＝0，δ＝1／4，那么立即可得

推論1假設H′1）成立，又存在兩個正數ρ1，ρ2且ρ1≠ρ2使得

那么邊值問題（1）至少有一個正解u，使得在ρ2和ρ2之間.

顯然，推論1中的f（t，u，－p）是可以變號的，并且也不要求maxf0，minf0，maxf∞，minf∞?｛0，＋∞｝，而且推論1中的條件H′3），H′4）也大大弱于文獻［5］的定理中的條件H5），H6），因此推論1大大優于文獻［5］的定理3.1.從而定理3推廣和改進了文獻［5］的定理3.1.

定理4假設條件H1），H2）成立，如果f∞，f0≥0，I2＞1，I3＞1，且存在b＞0，使得，其中

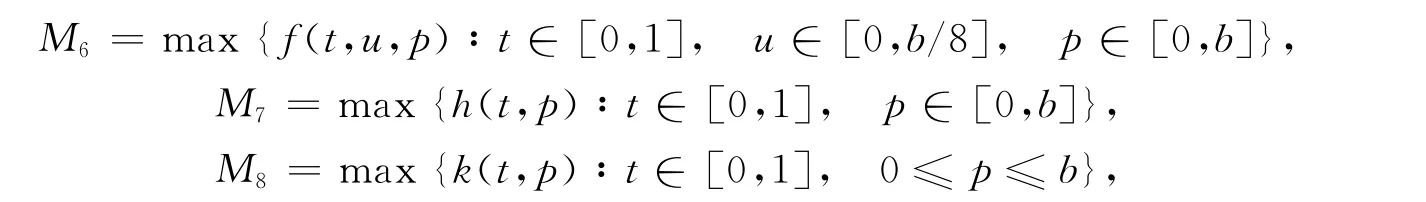
那么邊值問題（2）至少有兩個正解.

在定理4中，假設1＜I2，I3＜＋∞，但是當I2＝＋∞或I3＝＋∞時，定理4仍然成立.

［1］GPTA C P.Existence and uniqueness theorem for a bending of an elastic beam equation［J］.Appl Anal，1988，26（2）：289－304.

［2］MA Ru－yun，XU Ling.Existence of positive solutions of a nonlinear fourth－order boundary value problem［J］.Applied Mathematics Letters，2010，23（5）：537－543.

［3］MA Ru－yun，XU Jia.Bifurcation from interval and positive solutions of a nonlinear fourth－order boundary value problem［J］.Nonlinear Analysis，2010，72（1）：113－122.

［4］CUI Yu－jun，ZOU Yu－mei.Existence and Uniqueness theorems for fourth－order singular boundary value problems［J］.Computers and Mathematics with Applications，2009，58（7）：1449－1456.

［5］LIU Bing.Positive solutions of fourth order two－point boundary value problems［J］.Appl Math Comput.2004，148（2）：407－420.

［6］張興秋.奇異四階積分邊值問題正解存在唯一性［J］.應用數學學報，2010，33（1）：38－50.

［7］MA Hui－li.Symmetric positive solutions for nonlocal boundary value problems of fourth order［J］.Nonlinear Analysis，2008，68（3）：645－651.

［8］ZHANG Xue－mei，GE Wei－gao.Positive solutions for a class of boundary－value problems with integral boundary conditions［J］.Computers and Mathematics with Applications，2009，58（2）：203－215.

［9］KONG Ling－ju.Second order singular boundary value problems with integral boundary conditions［J］.Nonlinear Analysis，2010，72（5）：2628－2638.

［10］鄒黃輝，王全義.一類四階微分方程積分邊值問題正解的存在性［J］.華僑大學學報：自然科學版，2011，32（6）：699－704.

［11］郭大均.非線性范函分析［M］.濟南：山東科學技術出版社，2002：314－315.