應用多重分形奇異值分解 (MSVD)技術提取欽杭成礦帶南段文地地區Cu-Pb-Zn礦致地球化學弱異常*

呂文超，周永章，朱本鐸

(1.國土資源部海底礦產資源重點實驗室//廣州海洋地質調查局，廣東廣州 510075;2.中山大學地球科學系，廣東廣州 510275）

欽杭成礦帶位于楊子板塊與華夏古板塊的結合帶，南自欽州灣，北至杭州灣，全長2000 km，寬100 ～150 km，總體呈反 S 狀弧型分布［1－2］。它是極富特色的成礦域，擁有巨大的多金屬找礦潛力。

本研究區為欽杭成礦帶南段文地幅地區，有重要的成礦潛力，已發現多個金屬礦床，包括金山銀金礦、廉江銀金礦、澳通鉛鋅礦、君山鉛鋅礦、禾寮鋅礦等［3－5］，是重要的Cu-Pb-Zn多金屬成礦區。盡管前人做過一定程度的地質勘查研究［6－8］，但由于該區第四紀沉積物覆蓋較厚，隱伏礦體的Cu-Pb-Zn引起的地球化學異常十分微弱，阻礙了應用地球化學異常對該區Cu-Pb-Zn礦床的尋找。

多重分形是研究具有空間統計自相似性及分形結構在空間上的一種多重鑲嵌的一種結構，成礦過程產生的地球化學異常就具有這種多重分形分布的特征［9－10］。奇異性過程指在相對較短的時間或者空間內產生物質的超常富集、堆積或者巨量能量釋放的一種過程，這種過程在自然界中普遍存在，比如火山噴發、暴風雨、滑坡、森林大火、洪水等［11－13］。成礦過程也是一種奇異性過程，在其過程中所產生的礦床、礦致異常可以用冪率函數來度量，具有分形和多重分形的規律［9－10，14－16］。奇異性分析的目的就是在多次疊加、共同作用的復雜地質過程中，深層次挖掘出與成礦過程有關的信息。

前人研究顯示［17－19］，奇異值分解 (SVD)可以應用在垂直地震剖面中上行波、下行波和噪聲的分離，計算探地雷達圖像波反射總量，對噪聲和信號進行分離等。它是作為線性代數中用于矩陣分解中的一項重要方法，可以將數據集分解成一系列特征子空間。成礦過程是在一定時間和空間內的物質超常堆積和富集，這往往使得成礦作用結果的一些異常表現集中在一些相應的特征子空間中，這些特征子空間的能量與特征值平方之間的關系符合分形和多重分形分布，因此，應用分形分布的冪率函數可將不同特征子空間進行分離，可以更好的提取出與礦化有關的弱異常信息［20］。

1 多重分形奇異值分解技術原理

奇異值分解是在代數理論中非常有用的一種方法，它是將矩陣分解成左特征向量矩陣、對角矩陣和右特征向量矩陣的乘積。地球化學數據可以看作為一個矩陣X(m，n)。依據奇異值分解理論，可以進行如下分解:

其中，U為左特征向量矩陣，S為對角矩陣，也即奇異值矩陣，V是右特征向量矩陣，T代表矩陣的轉置。矩陣S中的數值即為矩陣X的奇異值，且沿對角線降序分布，這些奇異值的分布符合分形和多重分形分布，可以用冪率函數描述［10，20－23］，其值大小為矩陣XXT或XTX特征值的正平方根，即

其中，r為矩陣X的秩，σ1≥σ2≥…≥σr＞0，σi=奇異值矩陣分解還可以寫成如下的形式:

式中，r是矩陣X的秩，σi是矩陣X的第i個特征值，ui和vi分別是XXT和 XTX的第i個特征向量，是一個m×m階矩陣，是原始矩陣X的第i個特征子空間。因此，應用式3可以應用全部的特征值重構出原始矩陣X，那么選取部分特征值進行重構，則將重構出含有原始矩陣部分信息的特征子空間。但是如何選取不同的奇異值來重構其對應的子空間是重建原始場，提取異常場的關鍵。前人通過研究［9］:這些特征值在雙對數圖中存在不同的多重分形特征 (冪率關系)，依據曲線的不同斜率，用不同的直線段分別對曲線擬合，不同線段的交點即為重構中的分界點。

綜上所述，MSVD方法就是首先將地球化學數據看作為一個矩陣X(m，n)，其次應用基于MATLAB平臺編制奇異值矩陣分解程序分解出奇異值矩陣，然后應用多重分形方法確定奇異值矩陣的分界點，最后再應用MATLAB軟件編制的程序進行重構不同的特征子空間，奇異值所重構出的特征子空間往往與一定的地質過程相對應，以此達到異常場與區域場分離的目的。

2 MSVD對文地地區CuPbZn礦致地球化學弱異常的識別

2.1 研究區區域地質特征

前人曾對1∶50000文地幅所在的區域開展過一定的區域地質調查和研究［6－8，16］。這些前期工作為認識研究區的區域地質特征奠定了重要的基礎。結合前人研究成果和本研究地質測量工作發現(圖1)，該區出露的地層有白堊系和第四系，巖漿巖以酸性侵入巖為主，包括了研究區北部的茶子窩巖體和中部的英橋巖體。研究區混合巖大面積發育，巖性為均質混合巖、眼球狀混合巖、混合質片巖和混合花崗巖。該區構造線方向整體上呈北東向，兩條最大的北東向構造線為彭西垌－金坑斷裂帶和文地背斜。

圖1 文地區域地質圖Fig.1 Regional geological map of Wendi

2.2 CuPbZn地球化學礦致弱異常信息提取

本研究開展了研究區1∶50000水系沉積物的采樣和地球化學分析工作。采樣密度和采樣布局嚴格按中國地質調查規范進行。平均采樣密度4.27個/km2。將1 km2作為一大格，每一大格又分為4個0.25 km2的小格，嚴格控制在一個大格或連續5個以上小格沒有采樣點的情況出現。采樣物質以淤泥和粉細砂為主。采樣重量以過60目篩后達200 g為原則。

樣品分析送由江西省地球物理地球化學實驗測試所完成。分析項目為 Cu、Pb、Zn、Mn、Sn、W、Ag、Au、As、Sb、Bi、Mo、Hg、F 、Ba 和 B等16種。表1列出了用于本研究的Cu、Pb、Zn三種元素的此次測試分析方法、檢出限和報出率。

圖2(a)展示了Cu元素lnλ－lnE對數圖。根據特征值空間能量百分比和奇異值平方之間在不同區段之間存在的不同冪率關系，確定了3個區間。它們分別為λ1－λ3、λ4－λ23和大于λ23的3部分。λ1－λ3重構的空間能量所占總能量比例90%以上，反映的是區域Cu異常;λ4－λ23重構的空間反映的是局部礦致Cu異常;大于λ23的那部分能量所占百分比微忽其微，可能是一些微弱的礦致異常或者為一些各種來源的“噪聲”，可以忽略。

圖2(b)展示了Pb元素lnλ-lnE對數圖。根據特征值空間能量百分比和奇異值平方之間在不同區段之間存在的不同冪率關系，確定了3個區間。它們分別為λ1－λ2、λ3－λ16和大于λ16的3部分。λ1－λ2重構的空間能量所占總能量比例90%以上，反映的是區域Pb異常;λ3－λ16重構的空間反映的是局部礦致Pb異常;大于λ16的那部分能量所占百分比微忽其微，可能是一些微弱的礦致異常或者為一些各種來源的“噪聲”，可以忽略。

表1 分析方法和檢出限Table 1 Analytical method and detection limit

應用MSVD方法對研究區1∶50000水系沉積物地球化學數據分析的步驟包括［9，20－23］:首先將研究區水系沉積物地球化學數據Cu、Pb、Zn三種成礦元素分別看作為一個二維矩陣X(m，n)，然后應用基于MATLAB平臺編制奇異值矩陣分解程序分解出奇異值矩陣，再應用多重分形方法確定奇異值矩陣的分界點。

在借鑒熊德國提出的生產性生態足跡的核算公式基礎上，修正方愷（2018）提出的以全球平均生物生產力核算土地足跡的生態足跡模型，本文給出生物生產型生態足跡計算公式：

圖2 Cu、Pb、Zn元素ln λ-lnE對數圖Fig.2 ln λ vs lnE for Cu-Pb-Zn

圖2(c)展示了Zn元素lnλ－lnE對數圖。根據特征值空間能量百分比和奇異值平方之間在不同區段之間存在的不同冪率關系，確定了3個區間。它們分別為λ1－λ2、λ3－λ21和大于λ21的3部分。λ1－λ2重構的空間能量所占總能量比例90%以上，反映的是區域Zn異常;λ3－λ21重構的空間反映的是局部礦致Zn異常;大于λ21的那部分能量所占百分比微忽其微，可能是一些微弱的礦致異常或者為一些各種來源的“噪聲”，可以忽略。

本研究應用MATLAB軟件編制的程序對研究區Cu、Pb、Zn數據進行重構不同的特征子空間。

圖3(a)為Cu元素λ1－λ3重構的空間，反映的是區域Cu異常。圖3(b)為Cu元素λ4－λ23重構的空間，反映的是局部礦致Cu異常。

圖3(c)為Pb元素λ1－λ2重構的空間，反映的是區域Pb異常。圖3(d)為Pb元素λ3－λ16重構的空間，反映的是局部礦致Pb異常。

圖3(e)為Zn元素λ1－λ2重構的空間，反映的是區域Zn異常。圖3(f)為Zn元素3－21重構的空間，局部礦致Zn異常。

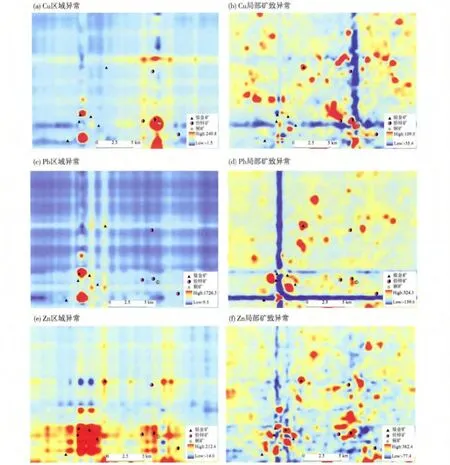
圖3 Cu-Pb-Zn元素異常圖Fig.3 The anomaly map of Cu-Pb-Zn elements

從以上各圖展示的分析結果可以看出，對Cu、Pb、Zn來說，盡管該區的鉛鋅礦上覆蓋層非常厚，整個原生成礦系統均被上覆蓋層掩埋，但經過MSVD提取的異常依然與鉛、鋅、銅等礦床 (點)吻合程度甚高。這說明了MSVD方法對本研究區隱伏礦床的弱致礦異常信息的提取是有效的。

3 MSVD方法與傳統方法的對比

將傳統統計方法確定的異常下限成異常圖并與MSVD方法所做的異常圖進行比較 (圖4)。

圖4 傳統方法和MSVD方法確定的Cu-Pb-Zn異常圖Fig.4 The Cu-Pb-Zn anomaly maps obtained by traditional and MSVD method

從以上的對比圖可以看出，在Cu、Pb、Zn異常方面，應用傳統統計方法圈定的結果，異常與Cu、Pb、Zn礦床并不吻合，礦點地區并未有異常出現。而應用MSVD方法圈定的結果，異常與Cu、Pb、Zn礦非常吻合。

通過實地野外地質填圖發現，研究區的鉛鋅礦上覆蓋層非常厚，整個原生成礦系統被上覆蓋層掩埋，只能通過長期的地質系統的作用下，隱伏的成礦系中所富集的成礦元素和微粒礦物質才有可能在覆蓋層中富集，形成弱異常。然而，研究區的Ag、Au礦Pb、Zn元素含量也比較高，而Ag、Au礦受斷裂帶控制。在研究區地表多見Ag、Au礦化脈的出露，Ag、Au礦化脈長期的風化剝蝕作用，不僅導致了Ag、Au異常的形成，也造成了Pb、Zn的高背景值，因此也影響了Pb、Zn較弱的礦致異常的識別，所以異常的識別和圈定相對較難。因此，微弱但有用的深部源致礦異常信息往往由于簡單的統計方法的使用而漏掉。

Cu、Pb、Zn致礦異常的提取表明，MSVD技術能夠克服Ag、Au礦引起的Cu、Pb、Zn高背景的影響，并從多重地球化學背景中有效提取致礦異常，包括低背景中的弱異常和隱蔽異常。該方法揭示了一系列Cu、Pb、Zn統計方法圈定的異常圖上沒有顯示的、規模不等的礦化異常，其中的一些異常和一系列礦床、礦點、礦化點重和，在未知區得到的弱異常也有進一步開展工作的意義，這為該區礦床勘查提供了新的靶區，為未知礦床的探尋提供了新的啟示。

4 結論

礦床的形成是復雜的地質過程和礦化過程的產物，而礦化過程往往具有多期次性，每一礦化期次都有可能導致地球物理和地球化學異常，導致了地球化學特征無論在平面上，還是在垂向上，宏觀上，還是微觀上，都呈現不均勻性，這使得地球化學空間分布格局上具有多重分形和奇異性的特征。而MSVD方法不是一個簡單的數學概念，它是能夠深入刻畫成礦過程的多重分形和奇異性特征的數理模型，與傳統方法相比，這種方法不僅可以研究地球物理場和地球化學場空間分布特征，而且可以區分地球化學場的背景以及與礦化有關的異常場。

本研究應用MSVD技術對研究區的1∶50000水系沉積物地球化學數據進行分析，表明該方法可以細致的刻畫研究區與礦化有關的局部地球化學異常特征，可以更加有效抑制非礦引起的地球化學高背景，更深層次提取Cu、Pb、Zn弱礦化異常信息。

［1］楊明桂，梅勇文.欽－杭古板塊結合帶與成礦帶的主要特征［J］.華南地質與礦產，1997，9(3):52－59.

［2］周永章，曾長育，李紅中，等.欽州灣－杭州灣結合帶(南段)地質演化和找礦方向［J］.地質通報，2012，31(2/3):32－37.

［3］周永章，曾長育，李紅中，等.欽杭成礦帶典型礦種及其礦床分布總體特征［J］.礦床地質，2010，29(增刊):34.

［4］呂文超，李紅中，安燕飛，等.礦產資源定量預測的研究進展［J］.礦床地質，2010，29(增):755.

［5］呂文超，楊志軍，周永章，等.欽杭結合帶南段和寮鉛鋅多金屬礦床石英的譜學特征及其指示意義［J］.光譜學與光譜分析，2013，33(5):1374 －1378.

［6］廣東省地質礦產局.廣東省區域地質志［M］.北京:地質出版社，1988:941.

［7］廣西狀族自治區地質礦產局.廣西壯族自治區區域地質志［M］.北京:地質出版社，1985:853.

［8］廣西壯族自治區地質礦產局.1∶5萬區域地質調查報告(文地幅和石角幅)［M］.北京:地質出版社，1985:145.

［9］成秋明，趙鵬大，陳建國，等.奇異性理論在個舊錫銅礦產資源預測中的應用:成礦弱信息提取和復合信息分解［J］.地球科學—中國地質大學學報，2009，34(2):232－242.

［10］成秋明，趙鵬大，張生元，等.奇異性理論在個舊錫銅礦產資源預測中的應用:綜合信息集成與靶區圈定［J］.地球科學—中國地質大學學報，2009，34(2):243－252.

［11］CHENG Q M.Non-linear theory and power-law models for information integration and mineral resources quantitative assessments ［J］.Mathemathecal Geosciences，2008，40:503－532.

［12］CHENG Q M，AGTERBERG F P.Singularity analysis of ore-mineral and toxic trace elements in stream sediments［J］.Computer＆ Geosciences，2009，35:234 －244.

［13］CHENG Q M，ZHAO P D.Singularity theories and methods for characterizing mineralization processes and mapping geo-anomalies for mineral deposit prediction［J］.Geoscience Frontiers，2011，2(1):67－79.

［14］張焱，成秋明，周永章，等.分形插值在地球化學數據中的應用［J］.中山大學學報:自然科學版，2011，50(1):133－137.

［15］張焱，周永章，黃銳，等.粵北劉家山地區多元素分形維數譜函數及其對礦化的指示分析［J］.中山大學學報:自然科學版，2012，51(2):119 －124.

［16］呂文超，周永章，張焱，等.欽杭成礦帶南段文地幅水系沉積物地球化學異常識別［J］.中山大學學報:自然科學版，2012，51(5):107－112.

［17］FREIRE S L M，ULRYCH T J.Application of singular value decomposition to vertical seismic profiling［J］.Geophysics，1988，53:778 －785.

［18］CAGNOLI B，ULRYCH T.Singular value decomposition and wavy reflections in ground-penetrating radar images of base surge deposits［J］.Journal of Applied Geophysic，2001，48:175－182.

［19］VRABIE V D，MARS J I，LACOUME J L.Modified singular value decomposition by means of independent component analysis［J］.Signal Process，2004，84:645－652.

［20］李慶謀，成秋明.分形奇異(特征)值分解方法與地球物理和地球化學異常重建［J］.地球科學—中國地質大學學報，2004，29(1):109－118.

［21］CHENG Q M.Multifractal distribution of eigenvalues and eigenvectors from 2D multiplicative cascade multifractal fields［J］.Mathematical Geology，2005，37:915－927.

［22］ZHAO B B，CHEN Y Q.Singular value decomposition(SVD)for extraction of gravity anomaly associated with gold mineralization in Tongshigold field，Western Shangdong Uplifted Block，Eastern China［J］.Nonlinear Processes in Geophysics，2011，18:103 －109.

［23］WANG G W，ZHANG S T，YAN C H，et al.Application of the multifractal singular value decomposition for delineating geophysical anomalies associated with molybdenum occurrences in the Luanchuan ore field(China)［J］.Journal of Applied Geophysics，2012，86:109 －119.

［24］HAWKES H E，WEBB J S.Geochemistry in mineral exploration［M］.New York:Harper and Row，1962.

［25］黃瑞.化探數據處理方法研究——以攀西地區鉑族元素為例［D］.成都:成都理工大學，2005.

［26］李河江.若爾蓋地區地球化學異常數據處理研究［D］.成都:成都理工大學，2006.