IMS的開發(fā)與應用

雷婉南 趙鵬飛

(上海市測繪院，上海 200063)

隨著現(xiàn)代工業(yè)的發(fā)展，工業(yè)構(gòu)件的幾何尺寸越來越大，檢測精度要求也越來越高。工業(yè)測量系統(tǒng)是以獲得工業(yè)構(gòu)件的幾何參數(shù)為目的的軟硬件集成系統(tǒng)。目前，根據(jù)所用測量儀器的不同，可將工業(yè)測量系統(tǒng)分為以下幾類［1-6］:坐標測量機系統(tǒng)、激光跟蹤測量系統(tǒng)、經(jīng)緯儀工業(yè)測量系統(tǒng)、全站儀工業(yè)測量系統(tǒng)、近景攝影測量系統(tǒng)、激光掃描測量系統(tǒng)、iGPS工業(yè)測量系統(tǒng)等，系統(tǒng)的測量精度可達到亞毫米或更高級別。

其中前兩種屬于接觸式測量，對于無法到達的目標點具有一定局限性，其他均為非接觸式測量;激光跟蹤測量系統(tǒng)和iGPS工業(yè)測量系統(tǒng)的主要硬件設備價格昂貴;激光掃描測量系統(tǒng)數(shù)據(jù)采集容易，但數(shù)據(jù)后處理卻相對復雜;近景攝影測量系統(tǒng)國外發(fā)展相對成熟，但其價格也相對昂貴。

綜合考慮設備成本及實用性，利用兩臺全站儀，開發(fā)出一套操作簡便、實用性強的工業(yè)測量系統(tǒng)IMS。利用IMS可實時采集空間點的三維坐標，通過數(shù)據(jù)分析獲得被測物體的相關空間幾何參數(shù)，完成工業(yè)產(chǎn)品的質(zhì)量檢驗或裝配指導工作。

1 IMS的數(shù)學模型

IMS的數(shù)據(jù)采集基于空間前方交會原理，即通過測量空間點的方向值(包括水平方向和垂直方向)，實時獲得其空間三維坐標。

IMS的測量原理如圖1所示，其中A、B分別為兩臺經(jīng)緯儀(或全站儀)，P為空間點。參考文獻［7］將IMS的測量坐標系定義為:以經(jīng)緯儀A的結(jié)構(gòu)中心作為坐標系原點，以通過A結(jié)構(gòu)中心的鉛垂線為Z軸，取向上為正;以AB連線在水平面的投影為X軸，取A指向B方向為正;根據(jù)右手法則確定Y軸。

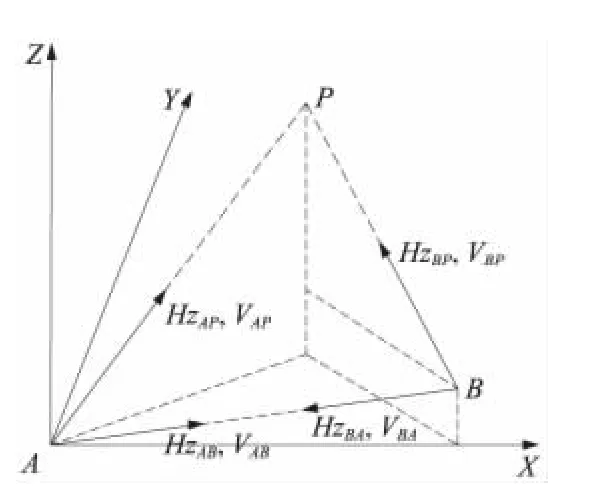
圖1 IMS的測量原理

通過觀測P點的方向值求解其空間三維坐標的過程如下:A、B互瞄，得互瞄的水平方向和垂直方向(取天頂距方向，以下同)觀測值分別為:HzAB，VAB，HzBA，VAB;然后用經(jīng)緯儀A、B分別觀測P點，得水平方向和垂直方向的觀測值分別為:HzAP，VAP，HzBP，VBP。則點P的空間三維坐標為

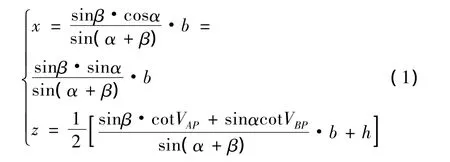
式(1)中:α =HzAB－HzAP，β=HzBP－HzBA，b為A、B之間的水平距離，稱為基線長，可通過兩經(jīng)緯儀對某一長度基準測量進而反算得到·b，為兩臺經(jīng)緯儀的高差。

2 IMS系統(tǒng)設計與構(gòu)成

IMS的硬件主要包括兩臺經(jīng)緯儀(或全站儀)，基準尺，數(shù)據(jù)傳輸線，數(shù)據(jù)接口轉(zhuǎn)換器等。

IMS測量流程如圖2所示，主要包括以下四個過程:①設備準備與初始化;②空間點測量;③數(shù)據(jù)分析;④成果輸出。

IMS主要包括三個子系統(tǒng):參數(shù)設置子系統(tǒng)、聯(lián)機測量子系統(tǒng)以及數(shù)據(jù)管理子系統(tǒng)，見圖3。

(1)系統(tǒng)參數(shù)設置子系統(tǒng)

單位設置包括長度、角度、溫度和氣壓等參數(shù)的設置;點誤差警告設置使用戶可按照工程精度要求設置誤差容限值及對應的警告顏色;基準尺參數(shù)設置包括基準尺尺長及誤差、基準尺編號、位置編號、端點號等的設置。

(2)聯(lián)機測量子系統(tǒng)

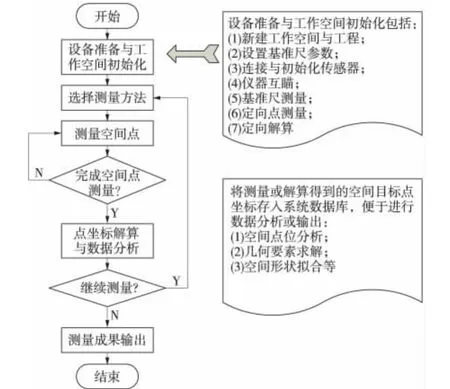
圖2 IMS基本測量流程

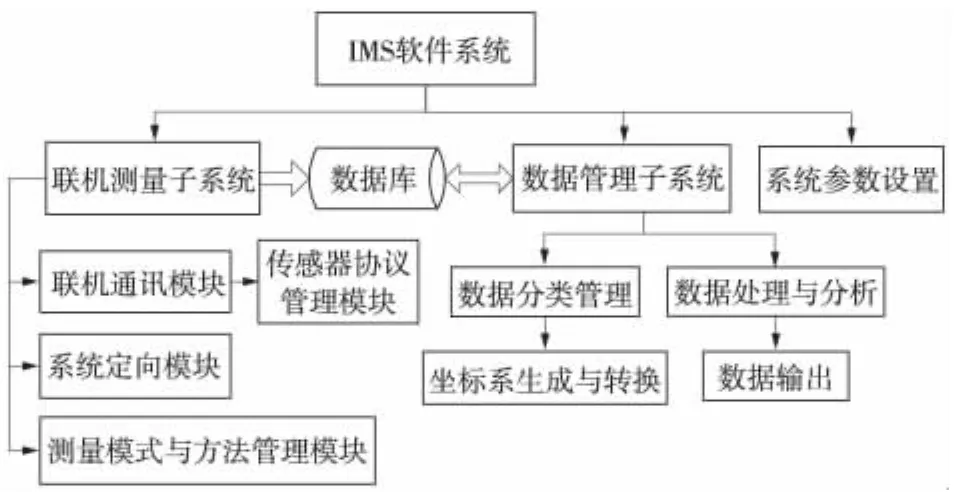
圖3 IMS的系統(tǒng)設計

聯(lián)機測量子系統(tǒng)包括聯(lián)機通訊模塊、傳感器協(xié)議管理模塊、系統(tǒng)定向模塊、測量模式與方法管理模塊。聯(lián)機通訊模塊用于實現(xiàn)計算機與傳感器的通訊;傳感器協(xié)議管理模塊用來封裝各傳感器的參數(shù)、指令與數(shù)據(jù)格式解析等;系統(tǒng)定向模塊用于定向解算，確定各傳感器的相對位置和姿態(tài)，從而建立一個統(tǒng)一的測量坐標系;測量模式與方法管理模塊向用戶提供多種測量方法，包括移站測量、偏移測量、隱蔽測量等。

(3)數(shù)據(jù)管理子系統(tǒng)

數(shù)據(jù)分類管理模塊用于數(shù)據(jù)的分類管理，以便實現(xiàn)數(shù)據(jù)的高效利用;測量數(shù)據(jù)處理與空間數(shù)據(jù)分析模塊封裝了點、線、面等的相關分析函數(shù)(如距離、角度、相交、平分計算，直線、平面、圓、球、橢圓柱等幾何形體的擬合計算等);坐標系生成與轉(zhuǎn)換模塊用于通過平移、旋轉(zhuǎn)、縮放、轉(zhuǎn)換參數(shù)和公共點最小二乘轉(zhuǎn)換等方式得到新的坐標系。

3 精度分析

根據(jù)誤差傳播定律［8］，對(1)式求偏導，可得空間點P在x、y、z三個方向的中誤差

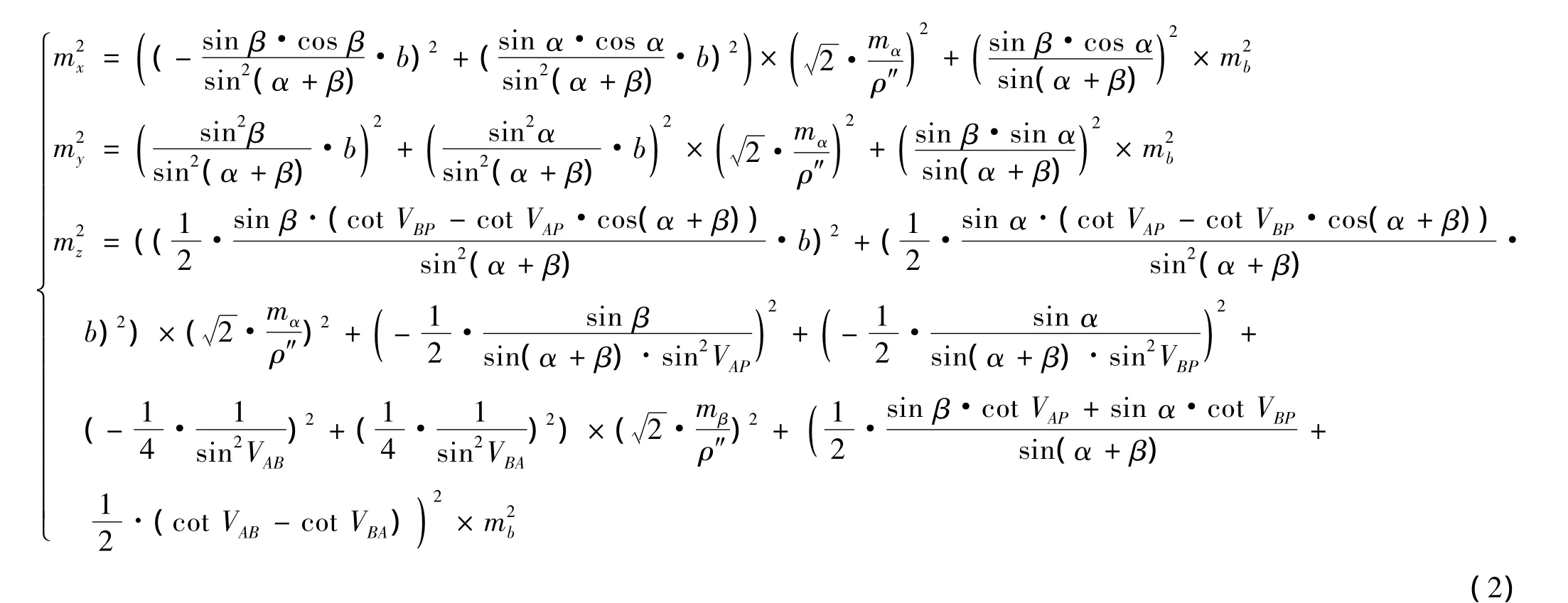
其中:ρ=206 265，mα、mβ分別為經(jīng)緯儀水平方向和垂直方向的觀測中誤差，mb為給定基線長誤差(單位為m)。

則P點的點位中誤差為

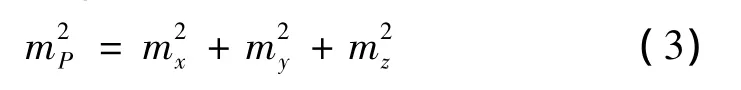
為得到系統(tǒng)的測量精度，以下進行系統(tǒng)實驗，包括單點測量實驗和反算距離驗證實驗兩個部分。

IMS系統(tǒng)實驗采用兩臺標稱測角精度均為0.5″的全站儀，而基準尺的尺長誤差約為±0.1 mm。在IMS完成系統(tǒng)定向后，測量空間某已知點R，兩臺儀器對R點的方向觀測值見表1，測量得坐標與已知坐標(見表2)，兩者在x、y、z三個方向的互差(測量坐標與已知坐標的差值)均為亞毫米級，由(2)式、(3)式得R點的點位精度為0.166 mm。

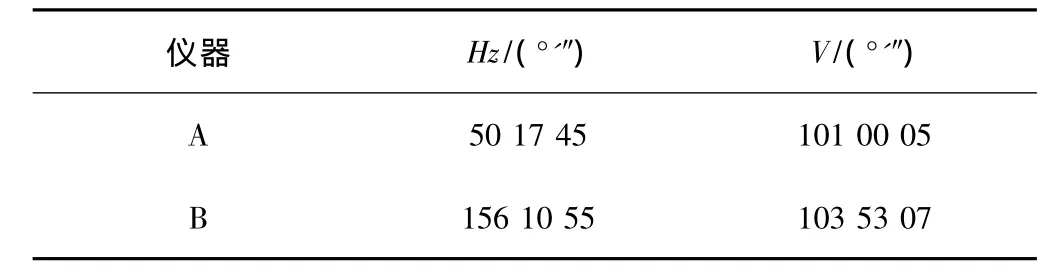
表1 R點的方向觀測值

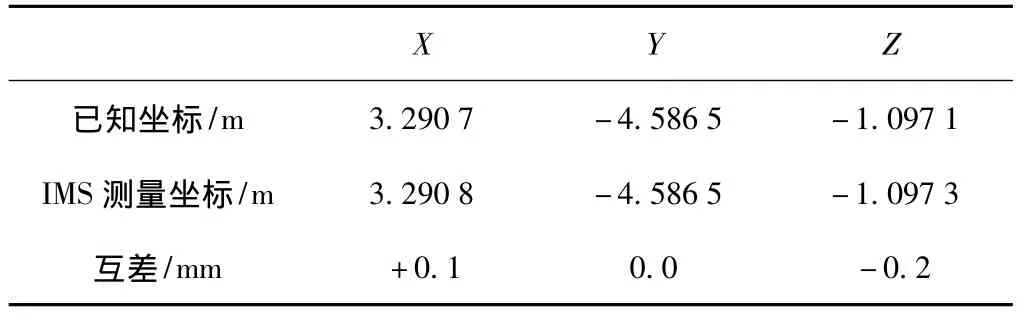
表2 R點的空間三維坐標

為進一步驗證IMS單點解算的正確性，利用IMS測量基準尺上的兩個固定點IS、IS1(兩點理論距離L=1.000 0m)，利用測量得到的三維坐標反算兩點間距離。為了讓實驗結(jié)果更加可靠，選擇3個不同的基準尺位置，在每個位置上，分別測量IS和IS1并計算其三維坐標，并利用IMS數(shù)據(jù)分析中的距離計算函數(shù)反算兩點間距離。

實驗中3個基準尺位置上解算出的點IS和點IS1的空間三維坐標見表3，反算距離與實際距離之差均在亞毫米級。

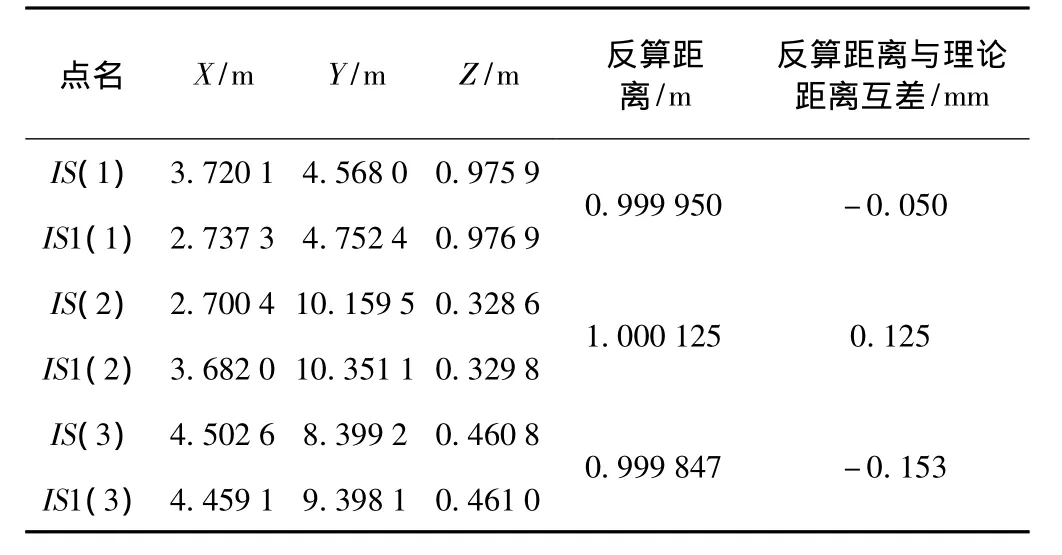
表3 基準尺的端點觀測值

通過對兩點間距離反算可得:利用IMS采集點的三維坐標反算距離與理論距離之差均為亞毫米級，實驗充分證明IMS精度高，具有強可靠性。

4 工程實例

IMS已成功應用于某工業(yè)構(gòu)件(球形儲罐)的檢測項目。被檢球形儲罐的設計半徑為6.000 0m，檢測目的是獲得球形儲罐的實際半徑。

項目使用高精度全站儀Sokkia Net05(標稱測角精度為0.5″，測距精度 ±(1+1 ×10－6D)mm，坐標測量采用無棱鏡模式，共采集18個均勻分布在球形儲罐表面的點的坐標，并計算出每個點到擬合球面的距離，見表4。參考文獻［9］［10］，得擬合的球面方程為

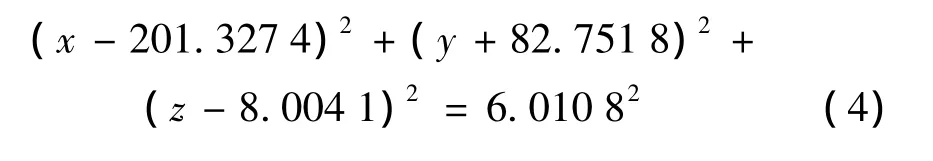
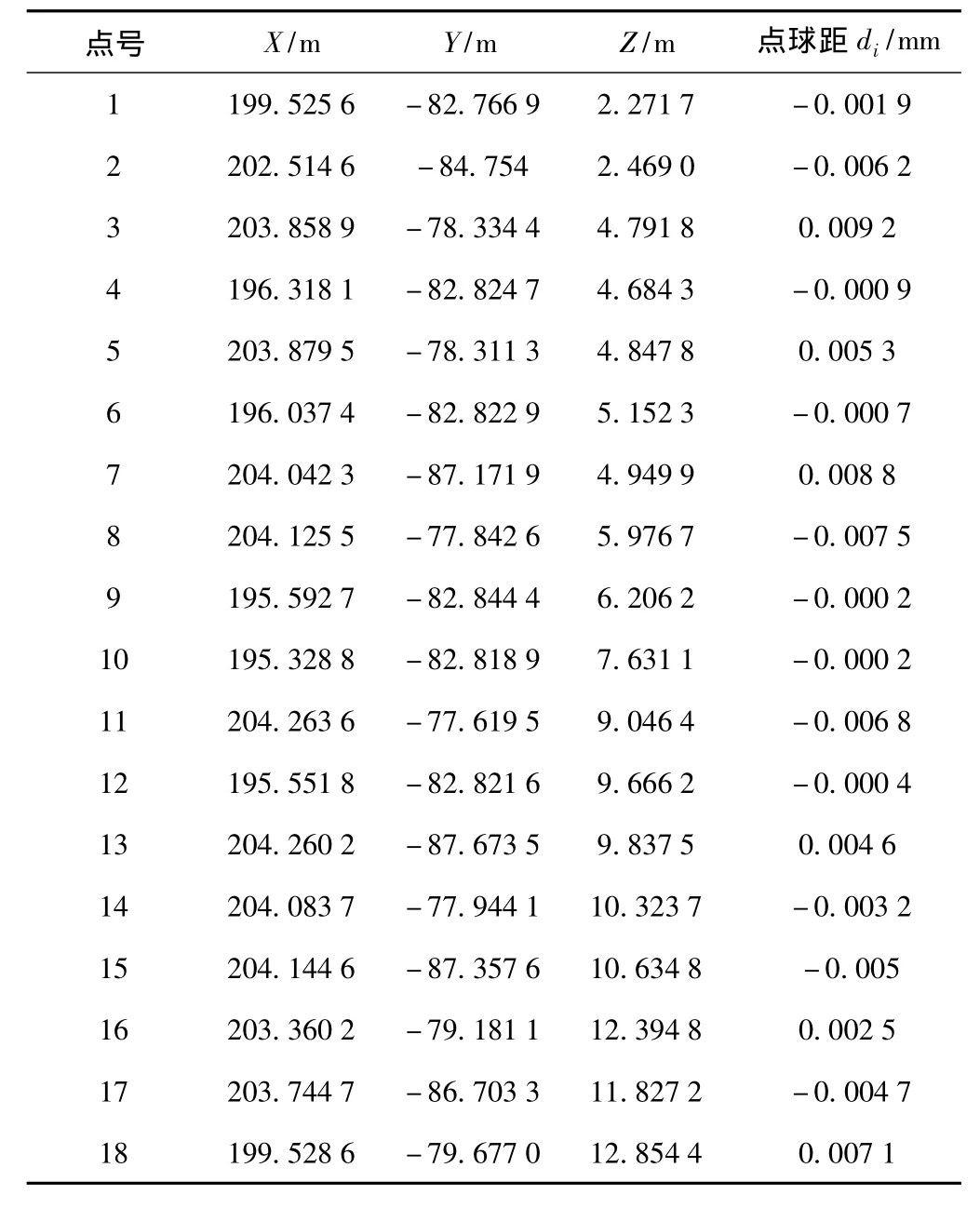
表4 工業(yè)構(gòu)件表面點三維坐標

并通過(5)式計算點球距中誤差

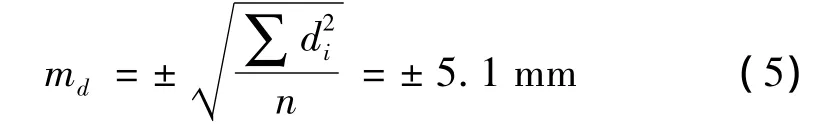
注:在該項目中，將兩倍的點球距中誤差作為限差，若某點的點球距超過限差，則認為此點觀測值為粗差，將其剔除并重新進行擬合分析。

由檢測結(jié)果可知:球形儲罐的擬合半徑為6.010 8m，與設計半徑相差1.08 cm，且點球距中誤差僅為5.1 mm，因此可認為該球形儲罐的尺寸是合格的。該工程實例驗證了IMS系統(tǒng)具有較強的可行性和實用性。

5 結(jié)論

IMS具有以下優(yōu)點:

①數(shù)據(jù)采集基于空間前方交會原理，數(shù)學模型可靠、穩(wěn)定。

②為無接觸測量，可觀測大尺寸目標，且對環(huán)境要求不高，適用于多種測量環(huán)境。

③界面友好，可視化工作界面便于用戶操作。

④具有一定的智能性，用戶可按照工程精度要求設置點位誤差容限值，在測量過程中可實時發(fā)現(xiàn)錯誤，剔除粗差。

⑤具有較完善的數(shù)據(jù)分析功能，能滿足常見工業(yè)擬合分析需求。

⑥有較高的精度，系統(tǒng)的硬件構(gòu)成和測量原理保證了系統(tǒng)可進行高精度測量，基本可滿足工業(yè)測量精度要求。

IMS也存在一些不足:

①僅實現(xiàn)了兩臺全站儀的通訊，還不能同時連接多臺全站儀。

②隨著現(xiàn)代工業(yè)測量目標的幾何尺寸越來越大，測量目標外形更加復雜，IMS的數(shù)據(jù)分析部分雖包括了常見擬合算法，但為適應工業(yè)測量發(fā)展，以便滿足多種擬合需求，IMS的擬合算法還有待擴充。

［1］黃桂平，李廣云，趙東印，等．經(jīng)緯儀工業(yè)測量系統(tǒng)定向及單點計算［J］．測繪學院學報，2001，18(2):93-96

［2］李廣云．工業(yè)三維坐標測量系統(tǒng)的最新進展［J］．測繪通報，1998(10):2-5

［3］鄭德華，沈云中，劉春．三維激光掃描儀及其測量誤差影響因素分析［J］．測繪工程，2005，14(2):32-35

［4］Kang S，Tesar D．Anoble 6-DOF measurement tool with Indoor GPS for metrology and calibration of modular reconfigurable robots．IEEE ICM International Conference on Mechatronics．Istanbul，Turkey:IEEE，2004

［5］馮文灝．V-STARS型工業(yè)攝像測量系統(tǒng)介紹［J］．測繪信息與工程，2000(4):43-47

［6］馮文灝．工業(yè)測量方法及其選用的基本原則［J］．武漢大學學報:自然科學版，2001(8):331-335

［7］黃桂平，李廣云．電子經(jīng)緯儀工業(yè)測量系統(tǒng)定向及坐標解算算法研究［J］．測繪學報，2003，32(3):256-260

［8］樊功瑜．誤差理論與測量平差［M］．上海:同濟大學出版社，1998

［9］王解先．工業(yè)測量中一種二次曲面的擬合方法［J］．武漢大學學報:信息科學版，2007(1):47-50

［10］雷婉南，趙鵬飛．逆向工程橢圓柱構(gòu)件的擬合計算［J］．大地測量與地球動力學，2010(5):102-105

［11］楊麗，樓立志．用擬合方法檢測空間圓形物體的變形［J］．鐵道勘察，2009(4)

［12］王解先，季凱敏．工業(yè)測量擬合［M］．北京:測繪出版社，2008

［13］潘國英，陳曉龍．空間圓形物體擬合新方法［J］．大地測量與地球動力學，2008，28(2)