基于UT變換改進多模型濾波的水下航行器導航方法
王澤元,許昭霞
(1.中國人民解放軍61818 部隊,北京102102;2.中國人民解放軍61081 部隊,北京100094)
0 引 言
由于組合導航技術具有導航精度高,可靠性強等優點,被廣泛應用于水下航行器導航系統[1]。對于組合導航系統的狀態估計,目前多采用卡爾曼濾波或擴展卡爾曼濾波對非線性模型進行線性化處理,這種處理方法存在2 個問題:一是由于忽略了模型的高階導數,估計精度隨著時間增長難以保證;二是濾波過程中需要反復計算系統方程的雅可比矩陣,濾波計算量偏大。
為克服卡爾曼濾波算法精度較低,易于發散,計算量大等缺點,Julier 針對非線性高斯模型提出了無跡卡爾曼濾波方法(UKF)[2]。已有學者運用無跡卡爾曼濾波方法解決水下航行器導航系統濾波問題[3-4],文獻[3]針對復雜加性噪聲,采用基于球面分布單形采樣,簡化了水下航行器組合導航的UKF 算法;文獻[4]針對無人水下航行器目標跟蹤控制需求,仿真驗證了UKF 估計方法的有效性。隨著多傳感器獲取信息融合提高導航精度,文獻[5]將UKF 引入到多模型濾波算法中,既能提高濾波算法的精度,也可并行求解,但是此方法的總體計算量偏大。此外,上述方法沒有考慮利用輔助信息對估計結果進行修正。
本文針對上述問題,將UKF 引入水下航行器組合導航系統濾波中,提出基于UT 變換的簡化多模型算法,同時設計融合算法,利用輔助信息對估計結果進行修正,提高整體估計精度。首先對非線性觀測方程進行UT 變化,利用Sigma 點構建偽觀測量,更新模型概率,得到偏差估計結果并代入到多模型濾波中,得到狀態估計結果。其次利用環境變量分析輔助信息可用度,提高系統魯棒性,并在此基礎上設計加權因子融合算法,合理利用輔助信息,提高系統整體估計精度。最后通過仿真驗證測試算法的有效性。
1 組合導航系統濾波模型的UT 變換
對于水下組合導航系統,線性化后離散系統數學模型如下[6-7]:
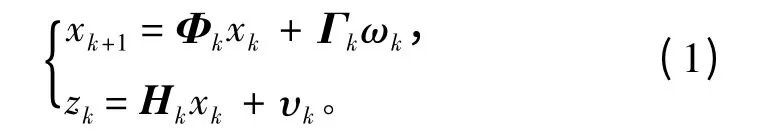
式中:xk為狀態向量;zk為觀測向量;Φk為狀態轉移矩陣;Γk為噪聲干擾矩陣;Hk為觀測矩陣;ωk,υk為零均值高斯白噪聲,且。
水下航行器組合導航系統建模為式(1)時,存在模型的近似和理想化假設,直接用于濾波會導致估計精度降低。考慮到系統非線性對觀測方程的影響,將式(1)的觀測方程表示為:
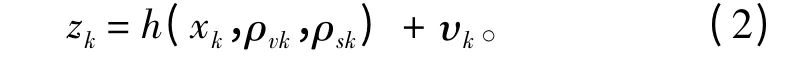
式中,h(·)為觀測函數;ρvk和ρsk為速度偏差和刻度系數偏差。
組合導航濾波系統中非線性特性表現在觀測方程,因此只需要對預測量進行采樣,然后利用觀測函數h(·)對采樣點進行處理,得到觀測更新后的系統統計特性。下面通過UT 變化產生Sigma 點對觀測方程進行近似,重新構建偽觀測量用于估計。
預測方程如下:

通過以下方法選取2nx+1 個sigma 點χi和相對應的權值wi,進行Sigma 點采樣:

為了避免UT 轉換后的方差陣為非正定陣,采用Julier[8]提出的尺度轉換方法對原始的sigma 點及其權值進行如下轉換:

其中,λ=α2(n+κ)- n,α 決定sigma 的散布程度,通常取α ≤1,κ 為比例因子,通常nx+κ=3,β 描述協方差計算χ0的權重,為求一階統計特性的權系數,為求二階統計特性的權系數。
觀測量更新如下:

觀測量和狀態量的交互協方差為:

若k 時刻觀測量為zk,則狀態估計結果及其協方差為:

2 輔助信息修正的改進多模型濾波算法
對組合導航系統濾波模型的UT 變換及狀態估計過程中,偏差值未知,下面首先基于sigma 點的偽觀測量進行偏差值的估計;然后利用輔助信息對估計結果進行修正,消除累積誤差,提高整體估計精度。
2.1 基于sigma 點的偽觀測量與偏差值估計
由式(8)可以看出,在偏差值ρvk,ρsk已知情況下,可通過UKF 方法得到系統狀態估計結果。下面利用式(5)生成的Sigma 點構建偽觀測量,然后通過改進多模型原理對偏差值進行估計。
假設ρvk,ρsk服從半馬爾科夫假設,利用離散值對其進行建模:

式中二維參數ρj的總數N=n·m。
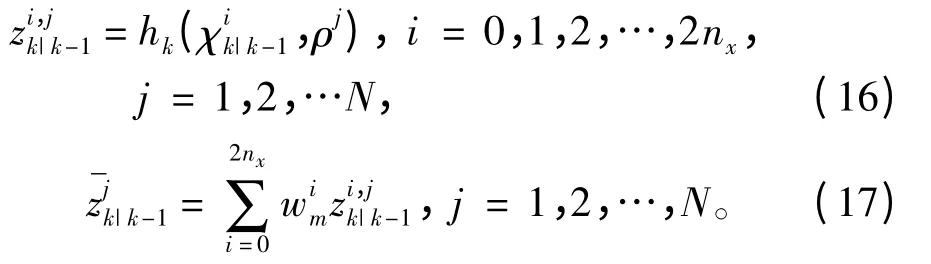
在觀測量zk已知情況下,構建偽觀測量的量測信息及其協方差陣:
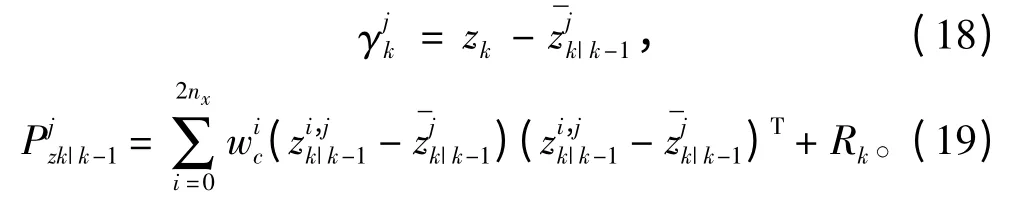
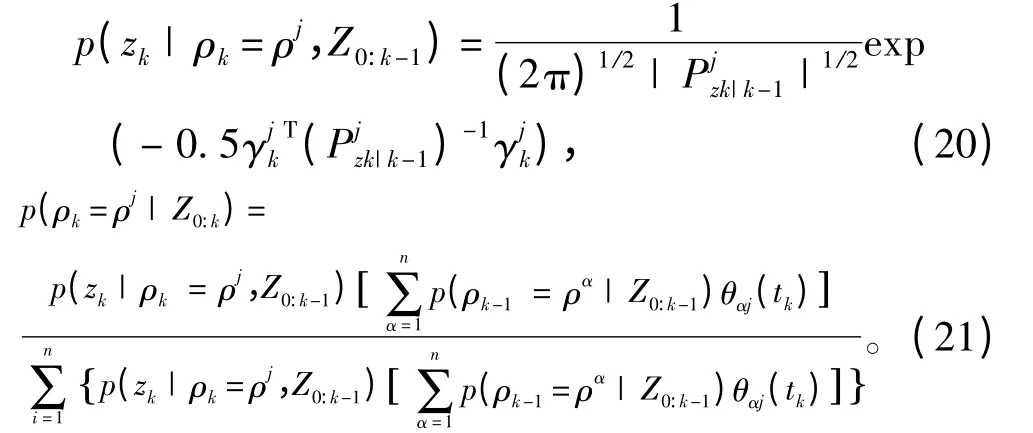
式中,p(ρk-1=ρα| Z0:k-1)為tk-1時刻偏差為ρα的概率,由遞推計算得到;θαi(tk)為tk時刻偏差ρα到ρj的馬爾可夫轉移概率,由概率轉移矩陣求得。
在ρj和p(ρk=ρj| Z0:k)的基礎上計算兩類偏差的估計值和:

2.2 輔助信息修正的改進多模型濾波算法
1)輔助信息的可信度分析
接收到的輔助信號z2觀測方程可表示為:

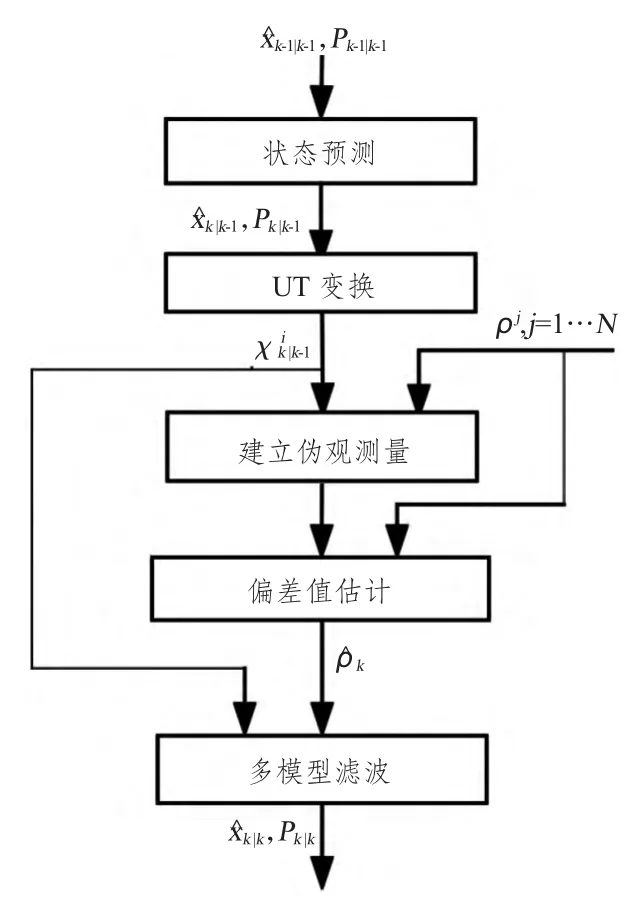
圖1 基于UT 變化的多模型濾波改進算法流程圖Fig.1 The flow chart of improved multiple model kalman filtering algorithm based on UT
式中:H2=[I,0];υ2k為零均值高斯白噪聲。采用卡爾曼濾波對輔助信息進行處理,得到狀態估計量和估計方差P2k。
環境信息變量描述傳感器數據的可用性,通過引入環境信息變量對傳感器進行分析,可以判斷傳感器信息的可行度,確保估計系統的整體精度。定義環境變量

式中,γk,Sk為觀測新息及其協方差陣,表達式為
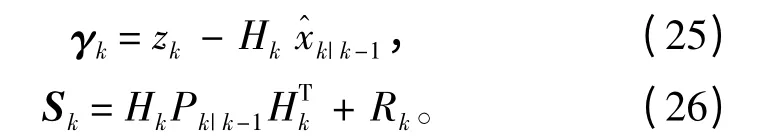
2)輔助信息的融合算法
在融合過程中需設置啟動閥λF,當λF=0,表示沒有獲得輔助信號,直接輸出多模濾波結果;當λF=1,表示得到輔助信號時,利用環境變量進行檢測,如果輔助信息可信度低,濾波過程中不考慮輔助信息,即
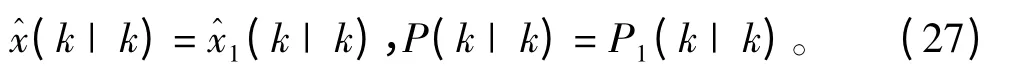
若輔助信號可用,則可以利用如式(28)所提加權因子法提高估計精度。

其中α1,α2為標量加權因子,表達式為

融合后狀態估計方差為

輔助信息修正的改進多模型濾波算法結構圖如圖2所示。

圖2 輔助信息修正的改進多模型濾波算法流程圖Fig.2 Improved multiple model kalman filtering algorithm used the auxiliary information
2.3 算法實現
輔助信息修正的改進多模型濾波算法的計算步驟如下:
第1 步:初始化
確定Sigma 點采樣的參數,計算初始狀態估計值、協方差陣。
第2 步:k 時刻濾波一步預測值
第4 步:觀測值更新

第5 步:輔助信息修正
判斷閥值λF,通過式(27)或式(28)得到融合后的狀態和狀態估計方差。
通過式(10)~式(12)計算狀態估計結果及其協方差。
3 仿真結果與分析
僅考慮在固定水深下的航行,水下航行器組合導航系統的仿真模型和條件同文獻[9],仿真時間取600 s。為了驗證本文提出方法的有效性,采用了本文方法和常規的多模型濾波算法進行了仿真,2 種方法在緯度和經度方向的位置誤差仿真結果如圖3和圖4所示。
由仿真曲線可知,采用本文算法可以有效地降低系統狀態誤差,加快濾波狀態收斂速度。
在估計精度方面,定義性能指標函數Jρv,Jρs為:

采用了本文方法和常規多模型濾波算法對偏差估計精度進行比較,表1 給出估計精度統計指標。
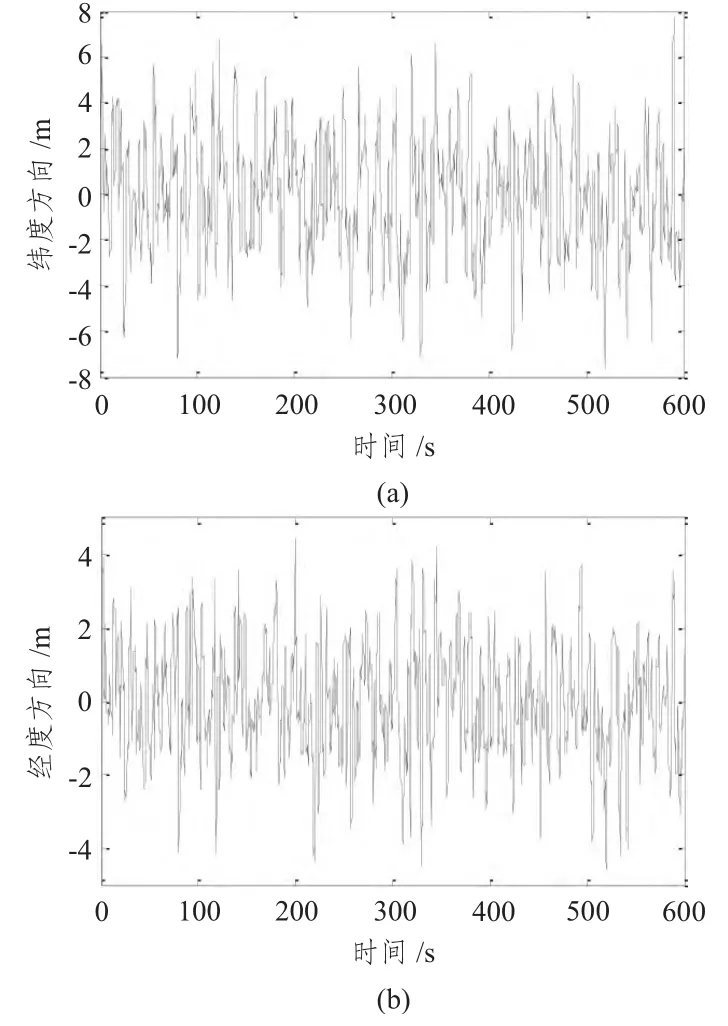
圖3 本文改進算法的位置誤差曲線Fig.3 Errors of position of improved algorithm

圖4 多模型濾波算法的位置誤差曲線Fig.4 Errors of position of traditional multiple model filtering algorithm
從表1 中的數據結果可知,本文算法通過UT變換對多模型算法進行修正,提高了估計精度。

表1 濾波算法估計精度Tab.1 Estimated accuracy of filtering algorithm
4 結 語
本文提出了一種基于UT 變換的簡化多模型算法,并利用輔助信息對估計結果進行修正。針對非線性觀測方程進行UT 變化,利用Sigma 點構建偽觀測量,進而更新模型概率,得到偏差估計結果并代入到多模型濾波中,得到狀態估計結果;然后利用環境變量分析輔助信息的可用度,設計加權因子融合算法,合理利用輔助信息,提高系統整體估計精度。
仿真結果表明所提方法有效地降低系統狀態誤差,加快濾波狀態收斂速度,同時對多模型算法進行修正,提高了估計精度。
[1]LI Kang-hua,WANG Jin-ling,LI Wan-li,et al.A noval INS and doppler sensors calibration method for long range underwater vehicle navigation[J].Sensors,2013,13(14):583-600.
[2]JULIER S J,UHHNANN J K.Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE,2004,92(3):401-422.
[3]劉明雍,胡俊偉,李聞白.一種基于改進無跡卡爾曼濾波的自主水下航行器組合導航方法研究[J].兵工學報,2011,32(2):252-256.
[4]王征.基于PF和UKF 的水下目標運動估計方法研究[J].自動化技術與應用,2013,32(12):12-17.
[5]朱安福,景占榮,高田,等.基于UKF 的交互多模型算法[J].系統仿真學報,2009,21(2):655-657.
[6]王其,徐曉蘇,張濤,等.模糊自適應濾波在水下航行器組合導航系統中的應用[J].中國慣性技術學報,2008,16(3):320-325.
[7]KIM H S,KIM I H.Design of adaptive fuzzy IMM algorithm for tracking the maneuvering target with time-varying measurement noise[J].International Journal of Control,Automation and Systems,2007,5(3):307-316.
[8]JULIER S J,UHLMANN J K,Durrant-Whyte H F.A new approach for filtering nonlinear systems[C].Proceedings of the American Control Conference,Evanston,USA,1995:1628-1632.
[9]HAO Yan-ling,MU Hong-wei.Application of integrated alignment in AUV based on GP-SRCDKF[J].Advances in Information Sciences and Service Sciences,2012,4(21):598-605.

