艦船大風浪航行轉向風險評估
劉 猛,張新宇,王 驍,王作超,石愛國
(海軍大連艦艇學院,遼寧 大連116018)
0 引 言
隨著我國海軍走向中遠海,艦船大風浪航行已成為常態,艦船大風浪航行的航法研究也就成為了目前迫切需要解決的課題。其中,艦船在大風浪中轉向風險評估重要性尤為突出。對中型艦船而言,風浪中轉向時機不妥、操作不當,往往是平時和戰時造成嚴重后果的主因之一。
艦船大風浪航行的轉向問題,航海界已經積累了豐富的應對經驗,值得很好地繼承和發揚。但這種方法通常是經驗性的,缺乏嚴格的定量依據,難以得到優化的結果。為此,本文提出了定量的艦船大風浪航行轉向風險評估方法,評估合格,可以視情轉向;評估達不到標準,不要輕易做出轉向決策,這樣大風浪安全航行就有了進一步的保證。
1 基本思路
艦船大風浪中轉向風險包括傾覆風險、破艙進水風險、設備損壞風險等,本文僅論述最主要的傾覆風險評估。艦船穩性包括靜穩性和動穩性,靜穩性曲線表征復原力矩隨橫搖角的變化,如圖1所示;動穩性曲線一般通過靜穩性曲線積分得到,即表征復原力矩做功隨橫搖角的變化,如圖2所示。艦船轉向過程中受到外力矩的突然作用,將以一定的角速度發生傾斜,屬于典型的動穩性問題。
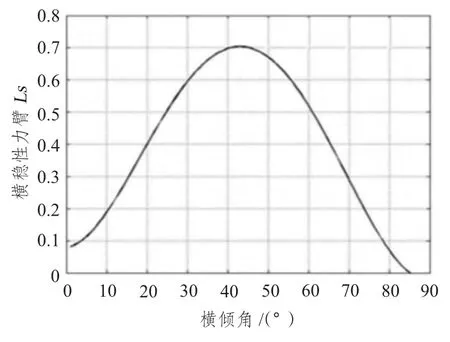
圖1 某驅逐艦靜穩性曲線Fig.1 A destroyer's statical stability curve
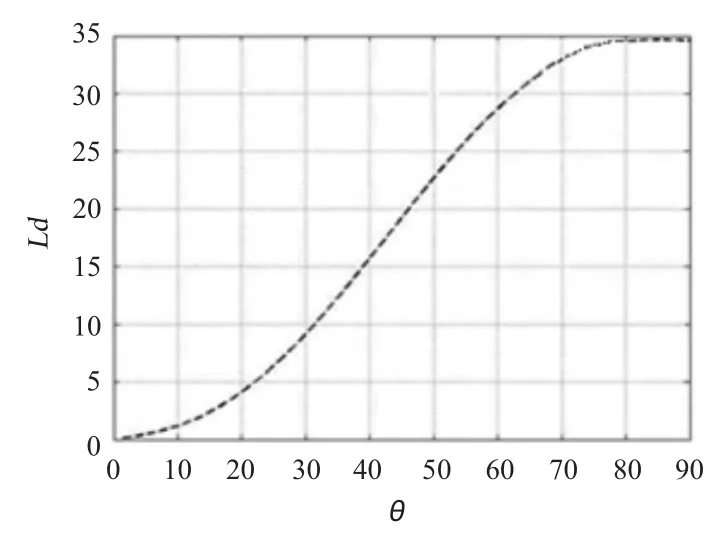
圖2 某驅逐艦動穩性曲線Fig.2 A destroyer's dynamical stability curve
艦船產生橫搖角θo時,浮心和重心不再處于同一鉛垂線上,由此產生復原力矩MR,當有一外力矩MH突然作用于船上,船體會加劇傾斜。若外力矩MH所做的功小于復原力矩所做的功時,艦船不會傾覆;反之,則發生傾覆;二者相等時,此外力矩MH即為艦船初始橫搖角θo對應的最小傾覆力矩[1]。外力矩做功在動穩性問題中,表示為斜直線。據此作動穩性曲線的切線,則切點所對應的縱坐標,就是兩力矩做功相當值,設為MHθ,θ 取單位弧度(57.3°),則對應的縱坐標就是最小傾覆力矩Mmin。當以力臂描述時,就是圖3 中的最小傾覆力臂lq。圖中的初始角,可取為艦船在波浪中橫搖的十一值θ1/10及旋回橫傾角θS之和。這樣,便可以從圖3的初始角A 點作動穩性曲線的切線,而切線的斜率,對應使船傾覆的最小外力矩,結合海上實際,就是艦船旋回傾側一舷的突風作用于船體的力矩。
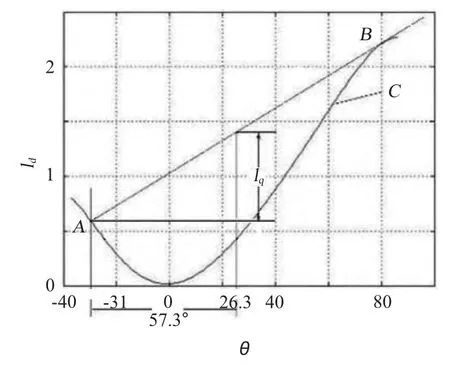
圖3 艦船最小傾覆力矩的幾何示意圖Fig.3 The geometric sketch of minimum overturning moment
2 數學模型及計算流程
艦船大風浪中轉向風險可以用穩性衡準數KQ來表示,其含義是艦船風浪中航行時,最大風傾力矩MW與最小傾覆力矩Mmin的比值。若此值接近甚至大于1,則艦船有傾覆危險,不宜轉向。
計算流程如下:
1)計算艦船穩定旋回的最大橫傾角θS;
2)計算艦船在轉向時刻海況下的十一橫搖值θ1/10;
3)確定初始橫傾角θmax= θ1/10+ θs;
4)計算以θmax為初始點的艦船動穩性曲線的切線;
5)求切點對應的Mmin或lmin;
6)計算突風對艦體作用力矩MW;
7)確定穩性衡準數KQ。
2.1 計算穩定旋回時最大橫傾角θs
艦船穩定旋回階段最大橫傾角:
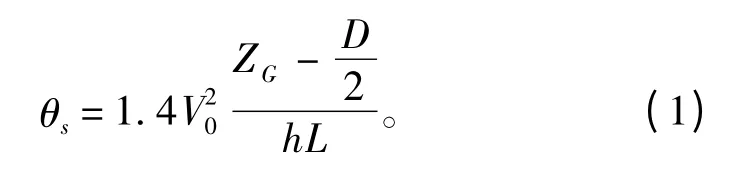
式中:V0為旋回前的直航速度;ZG為重心高度;D為吃水;L為船長;h為初穩心高。
2.2 計算橫浪中艦船橫搖角θ1/10
計算艦船在波浪中的橫搖角是一復雜課題。比較精確的計算模式是采用粘性流CFD (計算流體力學)的方法,但程序復雜、計算量大、用時長,目前不具備實時性。為此,本文采用勢流理論計算橫搖角,即根據轉向海域的海浪譜信息,借助基于勢流理論的艦船六自由度搖蕩程序,計算橫浪中艦船的橫搖十一值θ1/10。艦船六自由度搖蕩計算部分程序量約為16 K,共包含20個函數和18個組成變量,封裝在CShip 類里,計算流程如圖4所示。
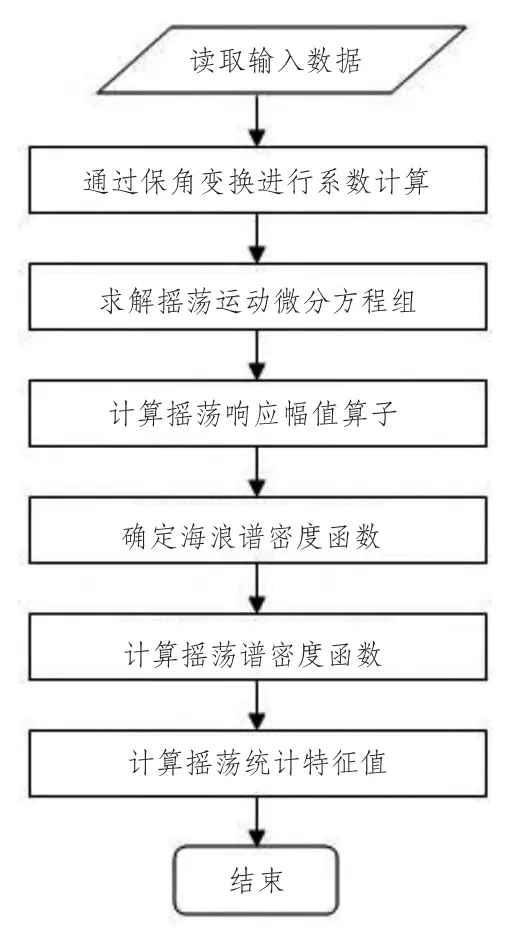
圖4 六自由度搖蕩計算流程Fig.4 The flowchart of 6 DOF motions calculation
2.3 計算大風浪中轉向最大橫傾角θmax
將橫浪中艦船的搖蕩十一值和旋回最大橫傾角線性疊加,作為艦船大風浪中轉向過程中最大橫傾角,即計算最小傾覆力矩的初始橫傾角:
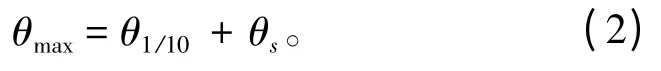
式中:θ1/10為橫搖十一值;θS為靜水旋回穩定橫傾角。
將θo= θmax作為初始橫搖角,進行艦船最小傾覆力矩Mmin的計算。
2.4 計算最小傾覆力矩Mmin
計算前需確定重量裝載變化量,若服役以來載荷變化量不超過D/10 (D為排水量),則按照艦船已知靜穩性曲線進行計算;如載荷變化量超過D/10 ,則按照未知穩性曲線進行計算,也就是說需要求解艦船靜穩性曲線。根據靜穩性曲線進行積分便可得到動穩性曲線。以橫搖角θo為初始角作動穩性曲線的切線,經處理便可求得在該海況下使船傾覆的最小力矩Mmin。
為提高橫搖角對應點和動穩性曲線切點的求解精度,可設動穩性曲線為一高次曲線,本文設為5次曲線,據此可得切點坐標為:
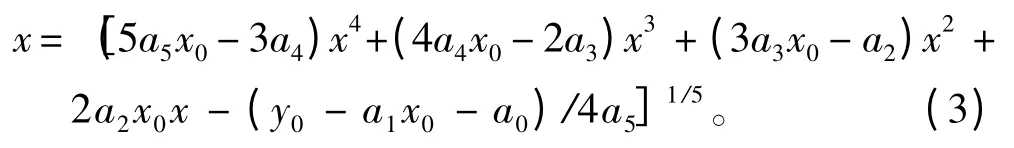
然后利用埃特金方法構造迭代法[2],迭代求解切線方程即可。
2.5 計算最大風傾力矩
1)計算相對風速:
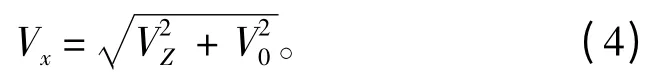
式中:Vx為相對風速;VZ為真風速;V0為艦船航速。
需要注意的是,在計算VZ時,應取突風,即陣風值,計算陣風的常用公式[3]如下:
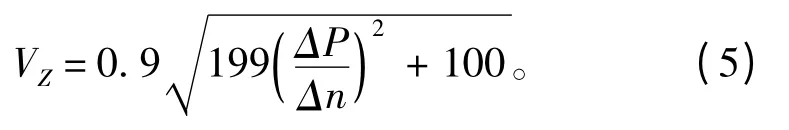
2)計算最大風傾力矩:

式中:VZ為真風風速;V0為航速;Vx為相對風速;AT為船體水面以上部分正投影面積;AL為船體水面以上部分側投影面積;LOA為總長;CfN為風力繞Z 軸轉矩系數,可以通過Isherwood 公式[4]求取:
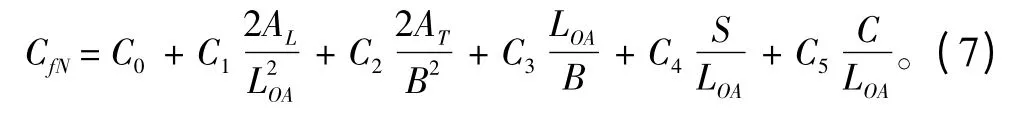
式中:S為船水上部分側投影周長,不包括水線、桅桿等細長體;C為船水上部分側投影面積形心至船首距離;M為桅桿、大柱等在側投影中分立的組數,不包括首柱遮蔽部分。
C0等系數隨相對風舷角βx變化的值如表1所示。
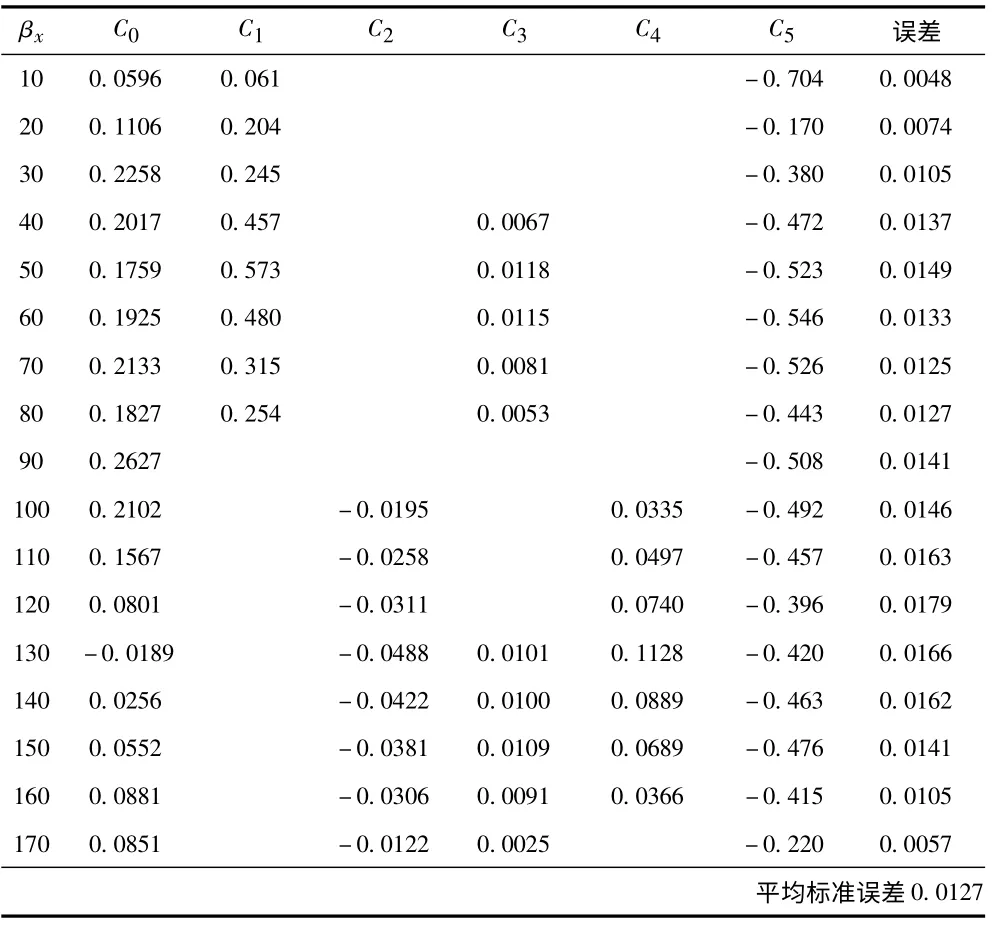
表1 Isherwood 公式系數表Tab.1 The coefficient table of Isherwood formula
2.6 穩性衡準數
穩性衡準數[5]是對船舶穩性的重要基本要求之一,對艦船的穩性計算要符合下列不等式:
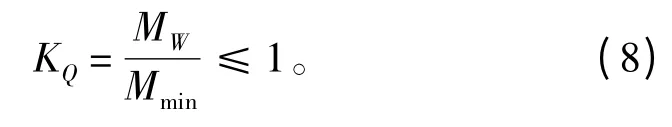
式中:KQ為穩性衡準數;MW為最大風傾力矩,表示在惡劣海況下風對艦船作用的動傾力矩;Mmin為最小傾覆力矩,表示艦船在最危險情況下抵抗外力矩的極限能力。
3 算例及驗證
本文選取海軍某型驅逐艦作為目標艦,在有義波高h1/3=4 m,風速VZ=18.92 m/s (8 級風)的海況下,目標艦(正常排水量)以初始航速V0=12 kn進行滿舵旋回,穩定旋回階段遭遇橫浪且橫向受風,對此時的穩性衡準進行了計算。目標艦穩性曲線如圖1所示,積分后動穩性曲線如圖2所示,相應計算結果如表2所示。

表2 計算結果Tab.2 The result of calculation
根據計算的KQ可以得出結論:此時艦船可以轉向,但需謹慎操作,防范風險。
本文主要對橫浪中艦船橫搖角的計算方法進行驗證,取比較權威的驅逐艦h1/3和θ1/3關系曲線[6]為基準,經擬合得到經驗公式為:
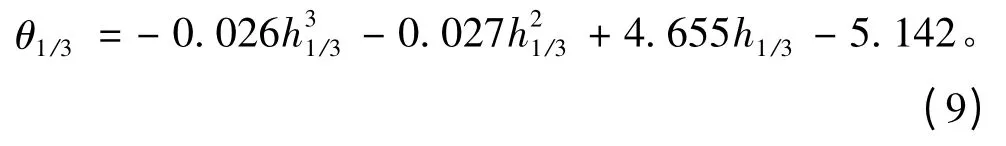
根據該公式得到h1/3=4 m 時,θ1/3=11.382°。按本文計算,結果為θ1/3=15.037°,基本吻合,間接證實了本文算法可信。
4 結 語
1)由于計算的相對復雜性,本文已將上述計算編成軟件,軟件界面如圖5所示。計算前需將目標船的型值及穩性數據輸入程序,另外,該軟件還考慮了轉向中艦體上浪和砰擊的風險。

圖5 艦船耐波性計算界面Fig.5 The interface of seakeeping calculation
2)在航海實踐中,艦船指揮員根據本文所研究的大風浪中轉向風險評估方法進行科學決策,轉向過程中再結合自身的航海經驗,可以有效地提高艦船轉向的安全性。
[1]盛振邦,劉應中.船舶原理[M].上海:上海交通大學出版社,2009:94-103.
[2]高望東,劉素珍.數值計算方法[M].大連:大連理工大學出版社,1992:9-10.
[3]喻世華,孫世剛.海洋天氣學[M].海軍司令部,1993:390-391.
[4]ISHERWOOD M A.Wind resistance of merchant ships[J].RINA Supplementary Papers,1973,115:327-338.
[5]許百春,等譯.船舶的耐波性和在波浪上的穩定措施[M].北京:國防工業出版社,1980:131-133.
[6]彭英聲.船舶耐波性基礎[M].北京:國防工業出版社,1989:47-50.

