微通道單相氣體流動特性影響分析

胡 廣，胡剛義，唐 瀅，彭學創

(中國艦船研究設計中心，湖北 武漢430064)

0 引 言

對于核動力裝置采用板狀燃料元件而言，其流道形狀是狹窄的矩形通道。在第4 代核反應堆設計中，研究者將燃料元件的間隙進一步減小，以期獲得更好的流動特性和經濟性。因此對矩形微通道內流體的流動方面需做更加深入的研究，以期為壓水堆的熱工水力研究提供一定參考，這也是本課題的研究意義。

本文采用徐建軍［1］的分類方法，將窄縫通道分3 類:窄縫寬度1 μm～1 mm為微通道;1～3 mm為窄通道;3 mm 以上稱為大通道。近年來，許多研究者開展了關于微通道的實驗研究。Kohl［2］測量了流體通過水力直徑為25～100 μm，對應Re 數范圍6.8～18 814和4.9～2 068的可壓縮和不可壓縮流動的流動特性。實驗摩擦阻力系數與理論值相當。

Wu和Little［3－4］測量了氣體通過水力直徑為55.81 μm，55.92 μm，72.38 μm的微通道的流動特性。摩擦阻力系數實驗值比理論值高10%～30%。而Yu［5］測得了氮氣通過水力直徑19 μm，52 μm，102 μm 微通道流動特性，得到摩擦阻力系數實驗值比理論計算值低。

相關實驗研究結果并不一致，有時候還互相矛盾。目前這種研究狀況表明微通道氣體流動特性影響機理尚未明了，仍需要建立合適的流動模型進行進一步的研究。而數值計算以成本低、速度快、具有較好模擬真實條件的能力等特點，對于類似本文中的已經能夠用數學模型描述的大多數問題，數值計算往往優于實驗研究，且不存在儀器測量上的困難和儀器本身的誤差［6］。

1 物理模型與控制方程

1.1 物理模型

所建立的矩形通道模型如圖1所示。本文研究的微通道分為2 種類型:當量直徑de=0.5 mm(通道1 尺寸為100 mm ×0.3 mm ×1.5 mm);當量直徑de= 1.0 mm(通道2 尺寸為100 mm ×0.6 mm ×3 mm)。假設流動為定常流動，工質為可壓縮理想氣體(空氣)。給定矩形通道進口速度，進口溫度為288.16 K，出口壓力為大氣壓。

1.2 控制方程

給出定常可壓縮牛頓流體運動的控制方程為質量守恒方程、動量方程、能量守恒方程和氣體狀態方程，如下所示:

質量守恒方程:

式中:U = U(u，v，w)為速度矢;▽·()表示對括號中的變量進行散度計算;

動量方程:

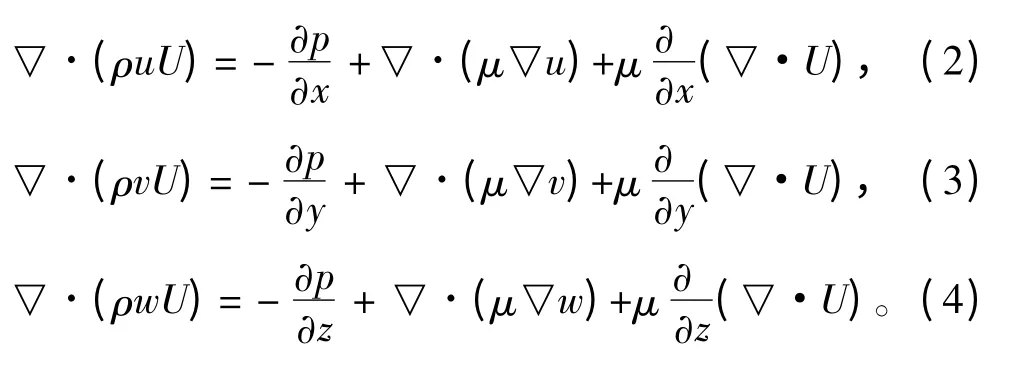
其中μ為氣體動力粘度;

能量守恒方程:

式中:源項ST等于耗散函數項與內熱源項二者之和;htot為流體的總比焓，定義為流體比焓h與1/2(u2+v2+w2)的和值;

狀態方程:

另加上當量直徑的定義:

式中:w為通道截面的寬;h為通道截面的高。

可壓縮流體流動中，氣體狀態方程將質量守恒方程、動量方程和能量守恒方程聯系起來，根據這個聯系，當流場溫度和壓力變化時，流體密度也可能會發生變化。R為氣體常數，數值為287 J/(kg·K)。

速度入口邊界條件:速度u =0，v =0，w為給定值，并且通過給定不同的進口速度改變進口雷諾數。

壁面邊界條件:無滑移，無熱量交換，固定壁面。

壓力出口邊界條件:選擇出口壓力為大氣壓。

為了較好地控制網格生成質量，選取結構化網格，劃分網格采用Patch Dependent 方法，網格類型選擇Tetra/Mixed。4 種通道平均網格量為310 000，可以保證有較好的計算精度。

圖1 微通道模型示意圖Fig.1 Schematic diagram of micro-channel

2 可壓縮性影響

在可壓縮流動中，將流場流速與聲速比較以表明可壓縮性的大小。馬赫數是衡量空氣可壓縮性的重要參數。在常規通道中，只有當馬赫數大于0.3 才考慮流體的可壓縮性。在微通道流動中，在馬赫數為0.2 時就必須考慮可壓縮性的影響［7］。本文在建模時考慮了可壓縮性，以便于說明其影響。

圖2 給出了當量直徑0.5 mm 通道1 時沿程速度分布情況。進口速度為10 m/s，20 m/s，40 m/s，80 m/s，120 m/s，分別對應進口雷諾數為345，690，1 380，2 760，4 140的5 種情況，對應的出口速度分別為16 m/s，32.5 m/s，65 m/s，100 m/s，150 m/s。從圖中可知，當進口雷諾數達到1 380時，可以直觀地看到速度變化，此時出口速度為65 m/s，馬赫數達到0.2，必須考慮可壓縮性影響。圖3 給出的是沿程平均馬赫數與進口雷諾數的對應關系圖。在圖3 中，當雷諾數為1 380 時，對應的平均馬赫數為0.15。

圖2 當量直徑0.5 mm 通道速度分布圖Fig.2 Velocity profile along channel with de =0.5 mm

圖3 當量直徑0.5 mm 平均馬赫數變化關系圖Fig.3 Mean Ma relatively to Re with de =0.5 mm

圖4 給出了當量直徑為1.0 mm(通道2)時沿程速度分布情況。可見，當進口雷諾數為2 760 時，出口馬赫數為0.2，需考慮可壓縮性影響。

圖5 給出了當量直徑1.0 mm(通道2)時的平均馬赫數與雷諾數變化關系圖。在該圖上可得到，進口雷諾數2 760 時，對應的平均馬赫數仍為0.15。

圖4 當量直徑1.0 mm 通道速度分布圖Fig.4 Velocity profile along channel with de =1.0 mm

在當量直徑0.5 mm，1.0 mm的微通道中，對應的平均馬赫數為0.15 時，此時需考慮可壓縮性的影響。以上分析表明對于微通道，平均馬赫數達到0.15 就需考慮可壓縮性。

圖5 當量直徑1 mm 平均馬赫數變化關系圖Fig.5 Mean Ma relatively to Re with de=0.5 mm

3 提前發生轉捩的影響

從上述分析可知，微通道在平均馬赫數達到0.15 即需考慮可壓縮性。為了研究的合理性，僅對平均馬赫數小于0.15的數據進行分析，此時，可以不用考慮流體的可壓縮性，當作不可壓縮流體進行后續影響因素的分析。

對于不可壓縮流體流動，不論是層流流動，還是湍流流動，其沿程阻力系數f 均按下式計算［8］:

式中:Δp為壓力降;de為當量直徑。

不可壓縮流體層流沿程阻力系數、湍流光滑管區沿程阻力系數表達式f 分別如下式所示:

式中C為Poiseuille 數。

圖6 給出了當量直徑0.5 mm 通道1的阻力常數的變化關系圖。前4 組平均馬赫數為0.04，0.08，0.15，0.27。這里為了便于分析，引入第4 組數據，但須了解第4 組數據需考慮流體可壓縮性。在常規通道中，根據高寬比為5，取C為75［9］。

圖6 阻力常數C與Re 變化關系圖Fig.6 Variation of friction constant C with Re

圖7 通道1 出口截面寬度方向速度分布圖Fig.7 Outlet velocity profile along width direction in channel 1

從圖6 中分析可得，Re ＜1 380 時，fRe≈78，此時微通道流體處于層流流動，沿程阻力系數f與常規通道差別不大。微通道在Re 等于1 380 左右后的曲線與湍流光滑管區曲線大致吻合，說明流場提前發生轉捩。但是數值計算得到的沿程阻力系數f比常規通道大，這是因為提前轉捩和可壓縮性將使速度分布更為飽滿，使微通道流動阻力增大，壓強降大于常規通道。同時也是導致通道速度偏離拋物線速度分布的原因。圖7 中給出了通道1 進口速度20 m/s 時，出口截面寬度方向的速度分布圖。從圖7 可以看到這種偏離，這一點與Guo［7］等的研究結果一致。

4 通道進口段影響

進口段的流動是速度分布不斷變化的流動，進口段以后的流動是速度分布較均勻的流動。

常規通道中，層流流動進口段長度為

經典理論中，湍流的進口段要短些，湍流進口段長度為

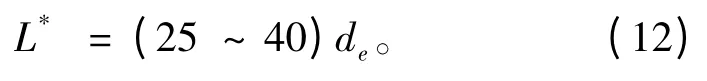
為便于分析，本文繪制當量直徑0.5 mm(通道1)的前4 組數據，對應的平均馬赫數為0.04，0.08，0.15，0.27，這樣第4 組數據同樣需要考慮可壓縮性的影響，且分開繪制，更加直觀。

圖8 當量直徑0.5 mm 通道壓力降示意圖Fig.7 Schematic diagram of pressure loss with de =0.5 mm

圖8 中，在進口0～0.02 m 區域，壓力損失較快，且曲線斜率先增大，然后減小，在0.02～0.10 m區域曲線斜率不變，接近直線。這是因為，受進口段影響，壓力降較大。在常規通道中，層流流動中壓力降與速度一次方成正比。在圖8(a)中，3 種情況的雷諾數分別為345，690，1 380，對于的層流流動進口段長度為0.01 m，0.02 m，0.04 m。從圖中可以直觀看出，受進口效應影響，微通道在0～0.01 m 區域壓強降較大，但在0.01～0.10 m 區域曲線斜率不變，接近直線。

在圖8(b)中，根據式(11)計算常規通道湍流進口段長度為0.012～0.02 m，大于微通道湍流進口長度。

上述分析表明，微通道受進口段影響，壓強降較大，但不論是層流進口段長度還是湍流進口段長度均小于常規通道。這是因為隨著尺度的減小，擾動增加，通道速度分布更加飽和，進口段效應會減弱。

5 結 語

本文通過對上述影響因素的分析，得出下列結論:

1)與常規通道馬赫數超過0.3 才考慮可壓縮性相比，微通道在平均馬赫數為0.15 左右就必須考慮可壓縮性，且該值受微通道特征尺度影響很小。且在進口雷諾數相同情況下，特征尺寸越小，速度越大，流動阻力增加，壓強降增大。

2)對于微通道，在Re為1 380 左右即提前發生轉捩。由于提前轉捩和可壓縮性，將使通道速度分布更為飽滿，沿程阻力系數比常規通道大，流動阻力增大，同時也是導致通道速度偏離拋物線速度分布的原因。

3)微通道受進口段影響，壓強降較大。由于微通道擾動較大，速度分布更飽和，進口效應減弱，所以不論是層流進口段長度還是湍流進口段長度均小于常規通道。

［1］XU J J，CHEN B D，WANG X J.Flow and heat transfer mechanism and key issues in a narrow channel［J］.Nuclear Power Engineering，2008，29(3):9－14.

［2］KOHL M J，Abdel-Khalik S I，JETER S M，et al.An experimental investigation of micro-channel flow with internal pressure measurements［J］.Heat and Mass Transfer，2005(48):1518－1533.

［3］WU P Y，LITTLE W A.Measurement of the friction factors for the flow gases in very fine channels used for microminiature joule-thomson refrigerators［J］.Cryogenics，1983，23:273－277.

［4］WU P Y，LITTLE W A.Measurement of the heat transfer characteristics of gas flow in very fine channels used for micro-miniature joule-thomson refrigerators［J］.Cryogenics，1984，24:415－423.

［5］YU D，WARRINGTON R O，BARRON R，et al.An experimental and theoretical investigation of fluid flow and heat transfer in micro-tubes［C］.Proceedings of ASME/JSME Thermal Engineering Joint Conf，Maui，HI，1995:523－530.

［6］PATANKAR S V.Numerical heat transfer and fluid flow［M］.New York:Hemisphere Pub.Corp.，1980.

［7］GUO Z Y，WU X B.Compressibility effect on the gas flow and heat transfer in a microtube［J］.Heat Mass Transfer，1997，40(13):3251－3254.

［8］KONG L.Engineering fluid mechanics［M］.Beijing:China Electric Power Press，2007.

［9］YANG Shi-ming.Heat transfer theory［M］.Beijing:Higher Education Press，2005.