期權(quán)定價(jià)中的隨機(jī)模型

許陽 羅旭 段白楊

(安徽工程大學(xué)數(shù)理學(xué)院,安徽蕪湖 241000)

期權(quán)定價(jià)中的隨機(jī)模型

許陽 羅旭 段白楊

(安徽工程大學(xué)數(shù)理學(xué)院,安徽蕪湖 241000)

隨機(jī)模型在期權(quán)定價(jià)中有著廣發(fā)的應(yīng)用,本文介紹了期權(quán)定價(jià)中的常見隨機(jī)模型,并分析了各模型的優(yōu)劣。

期權(quán)定價(jià) 隨機(jī)模型 布朗運(yùn)動

期權(quán)是一類重要的金融衍生產(chǎn)品，它賦予持有者將來某一時(shí)刻以實(shí)現(xiàn)約定的價(jià)格購買或出售一定數(shù)量資產(chǎn)的權(quán)利而非義務(wù)。1900年法國數(shù)學(xué)家兼經(jīng)濟(jì)學(xué)家巴切列爾首次提出用布朗運(yùn)動描述股票價(jià)格過程的變化，開創(chuàng)了隨機(jī)模型在期權(quán)定價(jià)中應(yīng)用的先河。巴切列爾在他的博士論文里假設(shè)股票價(jià)格在 t時(shí)刻價(jià)格為隨機(jī)變量St，在不相交的時(shí)間區(qū)間內(nèi)是獨(dú)立同分布的。并且在股票價(jià)格模型為(Bt為布朗運(yùn)動)情形下，得到了看漲期權(quán)的定價(jià)公式為

其中N(X)為正態(tài)分布的累計(jì)函數(shù)，φ(?)為標(biāo)準(zhǔn)正態(tài)分布的密度函數(shù)。該模型的缺點(diǎn)是：1)股票價(jià)格可能為負(fù)，并且在足夠長的時(shí)間里，期權(quán)價(jià)格會超過標(biāo)的資產(chǎn)價(jià)格；2)假設(shè)股票的期望收益率為零；3)模型未考慮時(shí)間價(jià)值。

在隨后的半個(gè)世紀(jì)，巴切列爾的工作都沒有引起重視，直到1961年Sprenkle才在股票價(jià)格服從對數(shù)正態(tài)分布的假設(shè)下提出了新的股票定價(jià)模型。Sprekle假設(shè)該分布中的股票價(jià)格平均值和方差是固定的，且價(jià)格有正向漂移，看漲期權(quán)價(jià)值公式為：

其中，參數(shù)π是“價(jià)格杠桿”的調(diào)節(jié)量.當(dāng)π的值是0時(shí)，就可得出期權(quán)的最終預(yù)期值。

隨后Boness將貨幣的時(shí)間價(jià)值引入到期權(quán)定價(jià)過程，他對股票收益假定了一個(gè)固定的對數(shù)分布，并且認(rèn)識到風(fēng)險(xiǎn)保險(xiǎn)的重要性。為簡明，他假定“投資者不在乎風(fēng)險(xiǎn)”。他利用這一假設(shè)證明了用股票的預(yù)期收益率α來貼現(xiàn)最終期權(quán)的預(yù)期值。他的最終模型是：

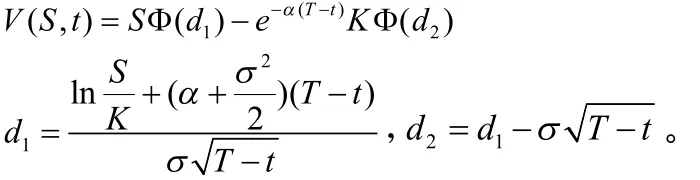
Samuelson于1965年認(rèn)識到，由于不同的風(fēng)險(xiǎn)特性，期權(quán)和股票的預(yù)期收益率一般來說是不同的他的歐式看漲期權(quán)的模型是：

其中d1與d2的定義與前面相同，而當(dāng)α=β時(shí)即為前面的Boness模型。

但是，上述期權(quán)定價(jià)理論都缺乏實(shí)用價(jià)值。1973年，Black和Scholes提出了股票著名的B-S期權(quán)定價(jià)模型，其服從以下幾條假設(shè)：

(2)允許使用全部所得賣空衍生證券；

(3)在衍生證券的有效期內(nèi)沒有紅利支付；

(4)不存在無風(fēng)險(xiǎn)套利機(jī)會；

(5)證券交易是連續(xù)的；

(6)無風(fēng)險(xiǎn)利率r為常數(shù)且對所有到期日均相同；

(7)允許使用全部所得賣空衍生證券；

并在此模型下得到了期權(quán)定價(jià)公式：

在B-S模型中的利率和波動率都是假設(shè)為常數(shù)的，而在實(shí)際中利率和波動率常常是一個(gè)變化過程。因此不少學(xué)者對利率和波動率模型做了一些改進(jìn)。其中常見的利率模型有：

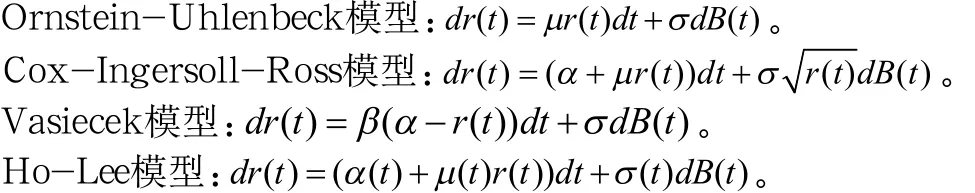
常見的波動率模型有：

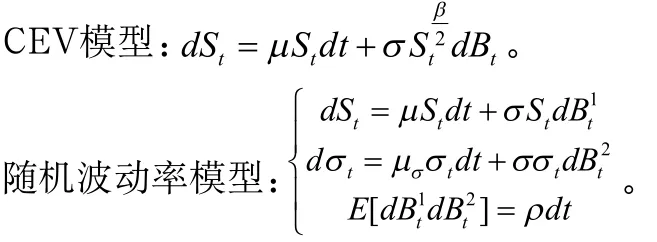
由于對股票市場的實(shí)證分析發(fā)現(xiàn)，股票價(jià)格常常受一些突發(fā)事件的影響使得價(jià)格發(fā)生跳躍，因此Merton提出了用泊松過程描述股票價(jià)格跳躍的股票價(jià)格模型：

其中N( t)為強(qiáng)度為 λ的泊松過程，Jt為跳躍高度這里 N( t)、Jt、B( t)相互獨(dú)立。

傳統(tǒng)的模型都是在股票服從對數(shù)正態(tài)分布下研究期權(quán)定價(jià)的，但是近年來對金融市場的大量研究發(fā)現(xiàn)，金融資產(chǎn)的價(jià)格過程并非服從對數(shù)正態(tài)分布，而是呈現(xiàn)尖峰肥尾現(xiàn)象，并且資產(chǎn)價(jià)格過程存在長相依性而非獨(dú)立增量過程。因此Peters提出了分形市場假說，分?jǐn)?shù)布朗運(yùn)動是一Hurst參數(shù)為 H(0＜H＜1)連續(xù)的Gaussian過程，滿足，并且。當(dāng)時(shí)，。分?jǐn)?shù)布朗運(yùn)動具有自相似性，即對α＞0，過程與過程有相同的有限維分布，并且當(dāng)即為標(biāo)準(zhǔn)布朗運(yùn)動時(shí)，分?jǐn)?shù)布朗運(yùn)動具有長期依賴性。Hu和ksendal建立了股票價(jià)格服從幾何分?jǐn)?shù)布朗運(yùn)動的期權(quán)定價(jià)模型：

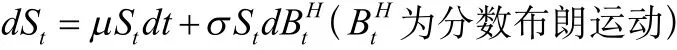
Hu和ksendal、Necula等利用Wick乘積下的隨機(jī)積分得到了歐式期權(quán)的定價(jià)公式。

分?jǐn)?shù)布朗運(yùn)動下的期權(quán)定價(jià)模型能更好的描述資產(chǎn)價(jià)格的長期依賴性和自相似性，并且實(shí)證研究也證實(shí)了金融市場的分形性質(zhì)。

[1]張衛(wèi)國,肖煒麟.分?jǐn)?shù)布朗運(yùn)動下股本權(quán)證定價(jià)研究[M].北京：科學(xué)出版社,2013.

[2]宋逢明.金融工程原理[M].北京：清華大學(xué)出版社,2003.

[3]林清泉.金融工程[M].北京：中國人民大學(xué)出版社,2013.

國家級大學(xué)生創(chuàng)新訓(xùn)練項(xiàng)目(201210363222),安徽工程大學(xué)教研項(xiàng)目(2012xjy59)。