基于RSSI測距的室內定位研究

周二林，王冠凌

(安徽工程大學 電氣工程學院，安徽 蕪湖 241000)

隨著物聯網相關技術的興起，基于無線傳感網絡(wireless ensing networks，WSN)和無線局域網(wireless local area networks，WLAN)等面向區域的定位技術越來越受到各行業研究者的關注。面向區域的定位技術是一個前景廣闊的研究方向，而室內定位技術是其中的典型代表。在眾多定位測距技術中，基于RSSI的測距定位技術通過發射點和接收點之間的信號強度值來估計兩點之間的傳播損耗，再根據經驗模型和相關理論知識將發射節點和接收節點之間的傳輸損耗轉換為兩點之間的距離，最后根據相應的算法推算出未知節點的位置。相比其他幾種常見的測距定位技術(如到達時間 TOA、到達時間差 TDOA、到達角 AOA等)，接收信號強度指示RSSI的測距定位技術對硬件的要求低、功耗小，且沒有時間同步，具有容易實現等優點，得到了廣泛的應用。但是復雜的室內環境使得定位精度較低，無法滿足正常的室內定位要求。另外，室內環境中人員走動帶來的突發性的干擾更使得室內定位的效果很難達到理想的程度，因此尋找一個比較理想的室內環境定位系統已經成為室內定位研究的熱點。

1 RSSI定位系統實現框架

在定位理論中，接收信號強度指示值RSSI測距定位技術是通過發射點和接收點之間的信號強度值來估計兩點之間的傳播損耗，再根據經驗模型和相關理論知識將發射節點和接收節點之間的傳輸損耗轉換為兩點之間的距離，最后根據相應的算法推算出未知節點的位置。由于室內環境的復雜性，經驗模型存在一定的誤差，以至接收信號強度值RSSI和未知節點的定位也先后存在不同程度的誤差。針對如何更精確的定位，本文提出的基于RSSI測距定位算法的流程如圖1所示。

圖1 定位系統流程

本文首先利用高斯濾波對采集的RSSI值進行預處理，然后根據數值越大的RSSI值對未知節點位置的參考價值就越大的思想，對高斯預處理后的RSSI值進行加權處理，并對轉換后的距離值進行最小二乘法修正。最后，通過判斷是否滿足判定要求決定是否重新定位。重新定位的次數人為設定，定位通過三邊測量算法來實現。

2 RSSI測距定位算法的實現

2.1 盲節點RSSI值的預處理

引用高斯濾波處理數據:首先，在同一個未知信標節點處采集n個RSSI值。由于室內環境的復雜性，往往存在一些小概率事件，通過高斯模型［1-3］濾除一些小概率、大干擾事件，以提高定位的準確性。其次，根據文獻［4］室內外環境下RSSI值與距離的衰減關系，當較近距離傳輸時，RSSI值衰減較快;當較遠距離傳輸時，衰減較慢，接收強度RSSI值相對傳輸距離的變化表現不明顯，即可以觀察到RSSI取值在10 m以內的衰減波動較大，在10～15 m衰減比較穩定，距離在15 m以外時，衰減變化很緩慢，因此參考價值比較小。因此，本實驗只取前15 m的實驗數據以滿足更為精確的定位要求。

信標節點可以通過RSSI值計算出未知節點與它的距離，電磁波能量P與路徑r的關系模型為其中:a為待定系數;P為能量值;r為距離。

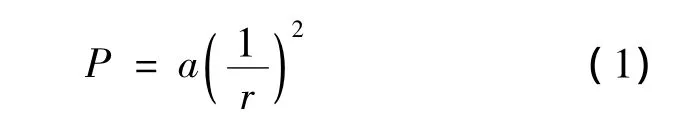
在實際測量過程中，RSSI有一個隨機分量x0，即實際測量的數值在一個穩定值附近上下波動，引入高斯模型:

其中:p0服從高斯分布，即 p0～N[ u，σ2]，密度函數為:

其中:xi為第i個信號強度值;n為信號數。

通過在同一個信標節點即同一個位置采集到n個RSSI值，根據采集到的RSSI值與均值u的偏離程度來判別RSSI值的準確性。同時，設定一閾值，當發生小概率的事件或干擾時，若RSSI值偏離均值大于設定的閾值，則排除該RSSI值;若RSSI值偏離均值小于設定的閾值，則保留所測得的RSSI值。

2.2 對信號強度加權處理

本算法的思路:在每個未知節點取n組RSSI值，數值越大的RSSI值對未知節點位置的參考價值越大。在每個測試點取n為100，經過高斯濾波后，對100個數據由大到小排序。取最大的前80個數據，然后將這80個數據分為4組，每組20個數據，分別記為A組、B組、C組、D組。對各組的數據求平均值，分別記各組 RSSIA，RSSIB，RSSIC，RSSID。

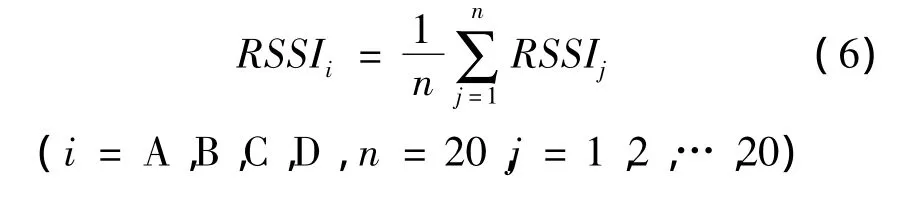
將上面4組數據分別乘以一個權重系數，權重系數值的大小與4組數據平均值的大小有關。假設RSSIA＞RSSIB＞RSSIC＞RSSID，則該參考節點的接收信號強度的平均值為

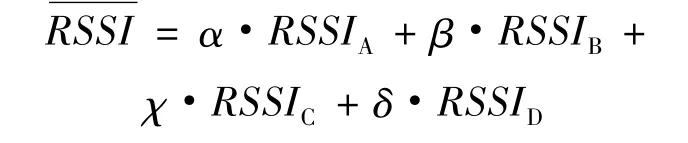
其中:α，β，χ，δ值的大小分別設為0.5，0.3，0.1，0.1。作為未知信標節點在該位置的信號強度。

2.3 利用最小二乘法修正距離值

在復雜的室內環境中，根據未知節點與信標節點之間的RSSI值估算距離必然存在一定的誤差，本文利用傳統的最小二乘法對由信號強度轉換后的距離值進行修正［5-6］。修正思想是在指定室內區域定位之前，先對特定區域環境進行大量實驗定位論證，以獲得該環境區域的定位結果的修正公式。方法步驟如下:

①根據具體的實際室內情況布置好參考節點和未知盲節點。假設參考節點坐標為(xi，yi)，盲節點坐標為(xj，yj)，盲節點和參考節點的坐標是人為設定的已知值，可根據兩點之間距離公式得到兩節點間的實際布置的距離值。

②根據接收信號的信號強度，通過與具體的室內環境相對應的距離損耗模型(式(1))來估算未知節點到各參考信標節點的距離Yi。

③通過最小二乘法來修正實際距離Xi與估測距離Yi的關系。設測距誤差值Y與實際距離值X之間存在線性關系，則Y=aX+b。根據最小二乘法原理，偏差平方和最小，則 G(a，b)=最小。通過 G(a，b)分別對a和b求導，令其等于0。則有:

根據真實值和誤差值，可求出a和b。那么修正后的距離為

其中:X為修正后的值，Y為距離估計值。通過最小二乘法的修正方法對由RSSI值轉換后所對應的距離值進行修正，可得到更加精確的距離值。

2.4 未知節點的坐標估計

針對未知節點的坐標估計采用最典型的三邊測量算法，其基本思想是:將這些節點按RSSI值從大到小的順序排序，選取最大的前3個參考節點作為本次定位的參考節點。通過最大的3個RSSI值得出未知節點到3個信標節點的距離值。已知固定節點(即參考節點)的坐標(x1，y1)，(x2，y2)，(x3，y3)，設未知節點的坐標為(x，y)。通過數學兩點之間距離知識可求導出各參考節點與未知節點之間的距離公式，通過兩兩相減可求出任意兩圓的交點所在直線。考慮到兩點確定一條直線，3個圓兩兩相交可確定3條直線，當3條直線有共同交點時，方程組有解，即為未知節點的位置;否則，方程組無解，放棄本次操作，重新獲取參數進行定位。通過這3個距離值計算出未知節點的位置［7-8］。

參考節點與未知節點之間的距離公式分別為:

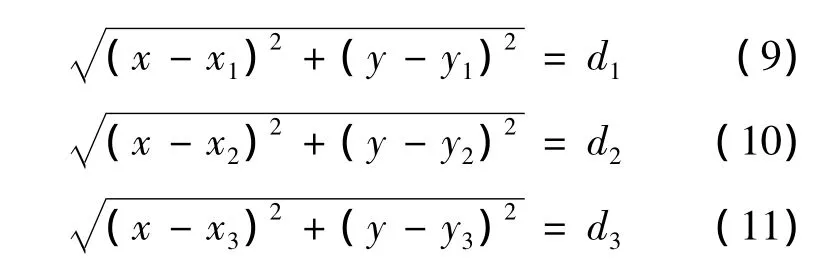
具體步驟:當信標節點 p1，p2，p3收到未知節點p發出的定位信號強度最大時，根據RSSI值，可以得到 p1到 p，p2到 p，p3到 p 的距離 d1，d2，d3;經過修正，分別以 p1，p2，p3為圓心，d'1，d'2，d'3為半徑作圓，通過這3個圓可確定未知節點［9］。

1)理想情況下:3圓有共同的交點，相交于P點，則P點坐標就是未知節點的坐標。由于算法操作存在一定的誤差，所以實際上3個圓不會相交于一點，而是一小區域面積。

2)實際情況下:由于環境復雜，存在誤差，所以一般情況下由3圓組成的區域交點分別為p1(x1，y1)，p2(x2，y2)，p3(x3，y3)。3 個圓兩兩相交可確定3條直線，判斷3條直線是否有共同交點。當有共同交點時，取Δp1p2p3的質心作為未知節點的估計位置。即

3)特殊情況:3個圓兩兩相交可確定3條直線，這3條直線沒有共同交點，即它們沒有兩兩相交，或者3個圓沒有任何交點，此時定位誤差較大，故放棄本次定位，重新獲取RSSI值，重復以上步驟重新定位，最大定位次數通過設定閾值來確定。通過重復定位可以克服一些突發和暫時性的干擾，比如人員的走動等。

3 實驗結果分析

實際的實驗環境比較空曠，沒有固定或移動的障礙物。選擇的場地為長18 m，寬6 m的實驗室，實驗中偶爾有人員走動。最后采用基于 Zigbee協議的CC2430/CC2431芯片為硬件平臺，利用RSSI信息來定位待測點的信息。

實驗統計數據如表1所示。RSSI均值為經高斯濾波處理后的RSSI值，然后直接求取RSSI均值。RSSI加權值為經高斯濾波處理后的RSSI值，再通過本文的加權算法進行處理后所獲得的RSSI值。均值誤差為RSSI均值經三邊算法定位所產生的誤差，加權誤差為RSSI加權值再經過最小二乘法修正和三邊算法所產生的誤差。

首先利用高斯濾波對采集的RSSI值進行預處理，然后根據數值越大的RSSI值對未知節點位置的參考價值就越大的思想，對所獲得的RSSI值進行加權處理，再對轉換后的測距值進行最小二乘法修正，最后，根據圓之間的交點個數，決定是否重新定位，定位的方法通過三邊測量算法來實現。在圖2中，實色曲線為本文的處理方法，虛色曲線為以往對RSSI取均值的方法。從圖2和表1可看出，本文所采用的測距室內定位算法的誤差范圍控制較理想，基本可以控制在-0.5～0.7 m，RSSI測距的精度較好。

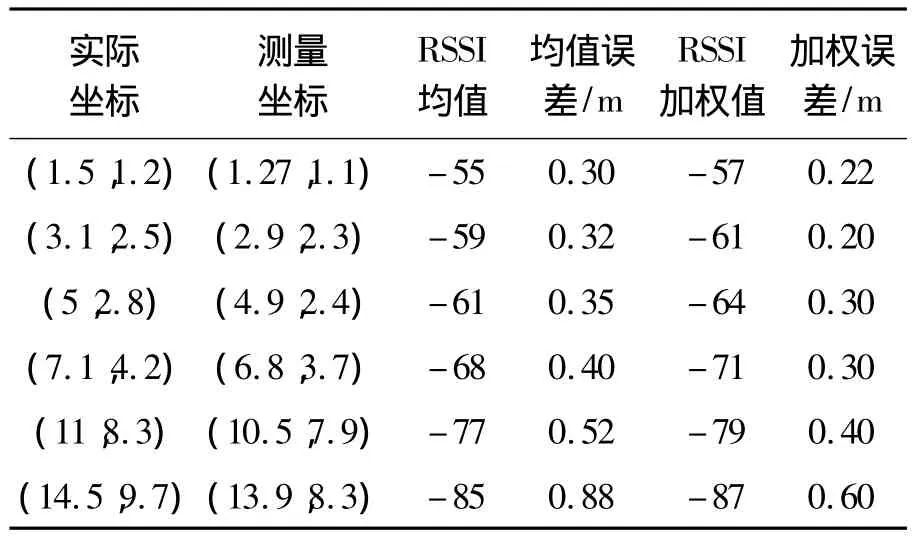
表1 定位數據表

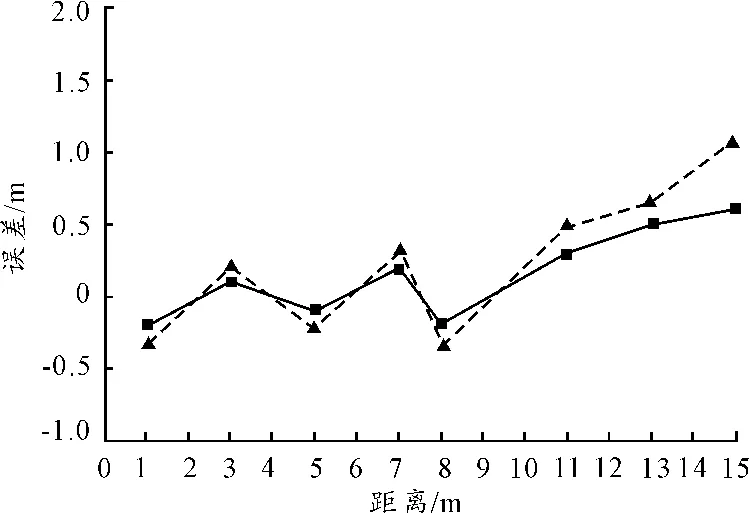
圖2 定位數據對比

4 結束語

本文對高斯預處理后所獲得的RSSI值進行加權處理和對轉換后的距離值進行最小二乘法修正以提高定位的準確性。通過實驗驗證了本文方法可提高室內定位精度的有效性和可行性，可基本滿足實際生活中的要求。由于本算法不需要增添額外的硬件開銷，所以具有較廣的實際應用范圍和較高的應用價值。

［1］劉文娟.基于RSSI測距的WSN定位系統設計［D］.大連:大連理工大學，2010.

［2］徐世武，王平.ZigBee技術中基于RSSI測距的定位算法研究［J］.福州:福建師范大學，2012.

［3］，Yaghmaee M H，Chiti zadeh J.Three dimension QoS deviation based scheduling in adaptive wireless networks［C］//MProceedings of the 21st International ConferenceAdvanced Networking and Applications.Washington DC:IEEE Computer Society，2007:588-595.

［4］徐久強，劉偉.基于RSSI的WSN抗干擾定位算法［D］.沈陽:東北大學，2010:647-648.

［5］章堅武，張璐.基于 ZigBee的RSSI測距研究［D］.浙江:杭州電子科技大學，2009(2):286-287.

［6］石為人，熊志廣，許磊.一種用于室內人員定位的RSSI定位算法［J］.計算機工程與應用，2010，46(17):232-235.

［7］趙昭，陳小惠.無線傳感器網絡中基于RSSI的改進定位算法［J］.傳感技術學報，2009:391-393.

［8］徐日明，莊長遠，俞斌.基于 RSSI的動態修正室內無線定位算法［D］.南京:南京航空航天大學，2010:686-688.

［9］臧建魁，卿粼波.基于RSSI和LQI分段距離估計改進算法［J］.通信技術，2011，11(44):100-102.